Dieses Kapitel enthält die folgenden Themen:

• Proportional und Antiproportional
• Berechnung

2.4 Grundlagen - Dreisatz

Der Dreisatz, auch Verhältnisgleichung oder Schlussrechnung genannt, ist ein üblicherweise dreischrittiges Verfahren, mit dem aus drei gegebenen Größen eine vierte berechnet werden kann, wenn die Größen in einem bestimmten Verhältnis zueinanderstehen. Bereits Adam Ries beschrieb dieses Vorgehen im 16. Jahrhundert in seinen Rechenbüchlein.

Proportional und Antiproportional

Zunächst müssen wir zwei wichtige Formen von Verhältnissen klären.

Zwei Größen heißen proportional zueinander, wenn sie sich im gleichen Verhältnis ändern. Das heißt: Verdoppelt sich die eine Größe, verdoppelt sich auch die andere. Verdreifacht sich die eine Größe, verdreifacht sich auch die andere. Wird die eine Größe durch $5$ dividiert, wird auch die andere Größe durch $5$ dividiert. Und so weiter …
Merksätze: „Je mehr, desto mehr.“ oder „Je weniger, desto weniger.“

Bei der grafischen Darstellung solcher Zuordnungen ergibt sich eine Ursprungsgerade:

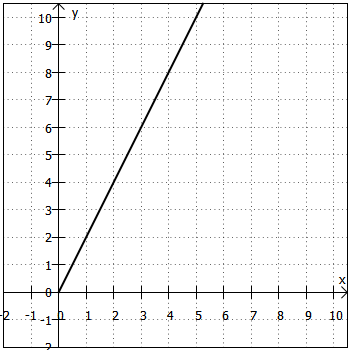
Zwei Größen heißen antiproportional (auch indirekt oder umgekehrt proportional) zueinander, wenn sie sich im umgekehrten Verhältnis ändern. Das heißt: Verdoppelt sich die eine Größe, halbiert sich die andere. Wird die eine Größe mit $3$ multipliziert, wird die andere durch $3$ dividiert. Wird die eine Größe durch $5$ dividiert, wird die andere mit $5$ multipliziert. Und so weiter …
Merksätze: „Je mehr, desto weniger.“ oder „Je weniger, desto mehr.“

Bei der grafischen Darstellung solcher Zuordnungen ergibt sich eine Hyperbel:

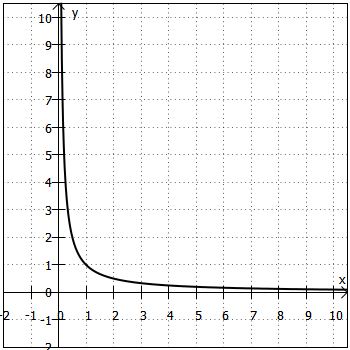
Berechnung

Ist ein Paar zusammengehörender Werte bekannt, kann über den Dreisatz ein zweites Paar berechnet werden, wenn dort nur ein Wert gegeben ist. Für die konkrete Berechnung schauen wir uns zwei Beispiele an.

Möchte man Eierkuchen für $3$ Personen backen, benötigt man $420\,g$ Mehl. Wie viel Mehl benötigt man für $8$ Personen?		Eine Tippgemeinschaft bestehend aus $5$ Personen hat im Lotto gewonnen. Jede/r von ihnen erhielt $55.800 \;\text{EUR}$. Wie viel Geld hätte jede/r gewonnen, wenn die Tippgemeinschaft aus $6$ Personen bestanden hätte?
Als erstes muss entschieden werden, ob eine proportionale oder eine antiproportionale Zuordnung vorliegt.
Für doppelt so viele Personen werden doppelt so viele Eierkuchen, sprich doppelt so viel Mehl, benötigt. Es handelt sich also um eine proportionale Zuordnung.		Besteht die Tippgemeinschaft aus doppelt so vielen Personen, ist der Gewinnanteil für jede Person nur halb so groß. Es handelt sich also um eine antiproportionale Zuordnung.
1. Schritt: Zunächst müssen die gegebenen Werte in eine Art Gleichung geschrieben werden. Praktischerweise sollte dabei die Größe, deren Wert gesucht ist, auf der rechten Seite stehen. Bitte achten Sie darauf, dass zwischen den Werten kein Gleichheitszeichen, sondern ein "entspricht"-Zeichen $\begin{array}{rcl}\widehat{=}\end{array}$ stehen muss. $3$ Personen sind sicher nicht das Gleiche wie $420\,g$ Mehl ...
2. Schritt: Bei beiden Varianten wird als Zwischenschritt die Entspricht-Gleichung so umgeformt, dass auf der linken Seite $1$ "Einheit" steht, was auch immer diese Einheit ist. Hier wird also berechnet, wieviel Mehl für "$1$ Person" nötig ist bzw. wieviel Geld "$1$ Person" bekommen würde. Dazu wird der Wert auf der linken Seite entsprechend multipliziert oder dividiert. Achtung 1: Beim Dreisatz wird nur multipliziert und dividiert, nie addiert oder subtrahiert! Achtung 2: Abhängig davon, ob es sich um eine proportionale oder antiproportionale Zuordnung handelt, unterscheiden sich die Vorgehensweisen! Bei einer proportionalen Zuordnung wird auf der rechten Seite exakt die gleiche Rechenoperation durchgeführt wie links. Bei antiproportionalen Zuordnungen ist die Gegenoperation nötig, sprich: Wird auf der linken Seite multipliziert, muss rechts dividiert werden und umgekehrt.
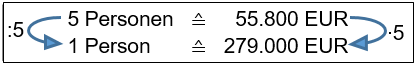3. Schritt: Wir formen weiter um, sodass sich in der dritten Zeile links der aus der Aufgabenstellung gegebene Wert ergibt. Auf der rechten Seite steht dann das Ergebnis. Achtung: Ebenso wie oben unterscheiden sich hier die Vorgehensweisen für proportionale und antiproportionale Zuordnungen.
Ergebnis: Möchte man Eierkuchen für $8$ Personen backen, benötigt man $1.120\,g$ Mehl.		Ergebnis: Würde die Tippgemeinschaft aus $6$ Personen bestehen, bekäme jede/r nur $46.500\;\text{EUR}$.

Eine Erkenntnis zum Abschluss: Die Einheiten verändern sich bei Dreisatzrechnungen nicht. Das führt insbesondere dazu, dass untereinander immer gleiche Einheiten stehen.

Worauf man achten muss

Es gibt natürlich auch Fragestellungen, bei denen die Größen weder proportional noch antiproportional zueinander sind.

Ein Beispiel: Zwei Musiker spielen das Lied „Happy Birthday“ in $25$ Sekunden. Wie lange brauchen vier Musiker? Natürlich hat die Anzahl der Musizierenden keinen Einfluss auf die Dauer – die Aufgabe klingt also nur nach Dreisatz … Man muss sich also immer vor der Dreisatzrechnung davon überzeugen, dass die Größen tatsächlich voneinander abhängig sind.

Auch das Eierkuchenbeispiel von oben ist durchaus problematisch: Wir sind stillschweigend davon ausgegangen, dass die Portionsgrößen alle gleich sind, sprich dass alle gleich viel essen. Dies muss aber nicht so sein: Stellen Sie sich vor, es kommen zwei kleine Kinder und sechs ausgehungerte Jugendliche zum Essen … Dann werden die Portionsgrößen sehr unterschiedlich sein. Nur zu prüfen, ob es sich um eine "Je mehr, desto mehr"- oder um eine "Je mehr, desto weniger"-Zuordnung handelt, ist also zu wenig. Es muss sichergestellt sein, dass jede Einheit gleich groß ist, gleich viel kostet etc. Insbesondere wenn viele Faktoren eine Größe beeinflussen, ist das häufig schwierig festzustellen.