Übersicht:

• Lösung zur 1. Aufgabe
• Lösung zur 2. Aufgabe
• Lösung zur 3. Aufgabe
• Lösung zur 4. Aufgabe

7.3 Lineare Gleichungssysteme - Lösungen

1. Aufgabe

1) Lösung nach dem Additionsverfahren
$\begin{array}{crclllcc} \text{I} & 3x+4y &=& -6 & \vert \cdot 5 \cr \text{II} & -5x-2y &=& -4 & \vert \cdot 3 \cr \cr \text{I} & 15x+20y &=& -30 \cr \text{II} & -15x-6y &=& -12 \cr \cr \text{I} & 15x+20y &=& -30 \cr \text{I+II} & 0x +14y &=& -42 & \Rightarrow y = -3 \cr \cr y=-3 \text{ in I} & 3x+4 \cdot (-3) &=& -6 &\vert +12 \cr & 3x &=& 6 & \Rightarrow x = 2 \cr \cr & \mathbb{L} &=& \{\left(2; -3\right)\} \end{array}$

2) Lösung nach dem Additionsverfahren
$\begin{array}{crclllcc} \text{I} & 2y+7z &=& 8 & \vert \cdot 8 \cr \text{II} & -16y-56z &=& 2 \cr \cr \text{I} & 16y+56z &=& 64 \cr \text{II} & -16y-56z &=& 2 \cr \cr \text{I} & 16y+56z &=& 64 \cr \text{I+II} & 0y+0z &=& 66 \cr \cr & \mathbb{L} &=& \emptyset \end{array}$

Bemerkung: Es gibt keine Zahlen $y$ und $z$, die jeweils mit $0$ multipliziert und dann addiert, $66$ ergeben. Das Produkt aus einer beliebigen reellen Zahl und $0$ ist immer $0$, die Summe von $0$ und $0$ ebenfalls. Daher ist diese Gleichung nicht lösbar.

3) Lösung nach dem Additionsverfahren
$\begin{array}{crclllcc} \text{I} & \dfrac{1}{4}x+\dfrac{3}{8}y &=& -\dfrac{5}{8} \cr \cr \text{II} & -\dfrac{1}{4}x-\dfrac{2}{3}y &=& \dfrac{1}{3} \cr \cr \cr \text{I} & \dfrac{1}{4}x+\dfrac{3}{8}y &=& -\dfrac{5}{8} \cr \cr \text{I+II} & -\dfrac{7}{24}y &=& -\dfrac{7}{24} & \Rightarrow y = 1 \cr \cr \cr y=1 \text{ in I} & \dfrac{1}{4}x+\dfrac{3}{8} \cdot 1 &=& -\dfrac{5}{8} &\vert -\dfrac{3}{8} \cr \cr & \dfrac{1}{4}x &=& -1 & \Rightarrow x = -4 \cr \cr \cr & \mathbb{L} &=& \{\left(-4; 1\right)\} \end{array}$

4) Lösung nach dem Einsetzungsverfahren
$\begin{array}{crclllcc} \text{I} & 3x+2y &=& 9 \cr \text{II} & 7x+y &=& 32 & \vert -7x \cr \cr \text{I} & 3x+2y &=& 9 \cr \text{II} & y &=& 32-7x \cr \cr \text{II in I} & 3x+2 \cdot (32-7x) &=& 9 \cr & 3x+64-14x &=& 9 &\vert -64 \cr & -11x &=& -55 & \Rightarrow x = 5 \cr \cr x=5 \text{ in II} & y &=& 32-7 \cdot 5 & \Rightarrow y = -3 \cr \cr & \mathbb{L} &=& \{\left(5; -3 \right) \} \end{array}$

5) Lösung nach dem Gleichsetzungsverfahren
$\begin{array}{crclllcc} \text{I} & 5y-\dfrac{1}{2}z &=& 10 &\vert& -5y \cr \cr \text{II} & 5y-\dfrac{1}{2}z &=& -14 &\vert& -5y \cr \cr \cr \text{I} & -\dfrac{1}{2}z &=& 10-5y \cr \cr \text{II} & -\dfrac{1}{2}z &=& -14-5y \cr \cr \cr \text{I=II} & 10-5y &=& -14-5y &\vert& +5y \cr & 10 &=& -14 \cr \cr \cr & \mathbb{L} &=& \emptyset \end{array}$

Bemerkung: $10=-14$ ist ein Widerspruch. Daher ist dieses Gleichungssystem nicht lösbar. Das hätte man allerdings auch ohne Rechnung erkennen können, da auf den linken Seiten der beiden Gleichungen jeweils der gleiche Term stand, aber unterschiedliche Ergebnisse vorgegeben waren. Für solche Gleichungssysteme kann es keine Lösung geben.

6) Lösung nach dem Gleichsetzungsverfahren
$\begin{array}{crclllcc} \text{I} & 3x-4y &=& -24 & \vert +4y \cr \text{II} & 3x+3y &=& 18 & \vert -3y \cr \cr \text{I} & 3x &=& -24+4y \cr \text{II} & 3x &=& 18-3y \cr \cr \text{I = II} & -24+4y &=& 18-3y &\vert +24+3y \cr & 4y+3y &=& 18+24 \cr & 7y &=& 42 & \Rightarrow y = 6 \cr \cr y=6 \text{ in II} & 3x &=& 18-3 \cdot 6 \cr & 3x &=& 0 & \Rightarrow x = 0 \cr \cr & \mathbb{L} &=& \{\left(0; 6\right)\} \end{array}$

7) Lösung nach dem Additionsverfahren
$\begin{array}{crclllcc} \text{I} & 52a+156y &=& -104 & \vert : 13 \cr \text{II} & -4a-12y &=& 8 \cr \cr \text{I} & 4a+12y &=& -8 \cr \text{II} & -4a-12y &=& 8 \cr \cr \text{I} & 4a+12y &=& -8 \cr \text{I+II} & 0a+0y &=& 0 \end{array}$

Die Gleichung I+II ergibt für alle reellen Zahlen $a$ und $y$ eine wahre Aussage. Die Lösung dieses linearen Gleichungssystems hängt also nur von Gleichung I ab. Da diese lineare Gleichung allerdings zwei Variablen hat, bekommen wir keine eindeutige Lösung. Wir müssen so tun, als wäre eine Variable fix. Wir nehmen hier mal hier mal an, dass $y$ als reelle Zahl festgelegt wäre (mit $a$ würde es aber genauso funktionieren). $y$ wird damit zu einem sogenannten Parameter. Dann können wir Gleichung I so umformen, dass $a$ alleine auf einer Seite steht:

$\begin{array}{crclllcc} \text{I} & 4a+12y &=& -8 & \vert & -12y \cr & 4a &=& -8-12y & \vert & :4 \cr & a &=& -2-3y \cr \cr & \mathbb{L} &=& \{\left(-2-3y; y\right) \text{ mit }y \in \mathbb{R}\} \end{array}$

Wir bekommen also nur dann eine Lösung des Gleichungssystems, wenn $a=-2-3y$ ist. Da wir $y$ ja selbst bestimmen dürfen, finden wir von diesen Zahlenpaaren dann aber unendlich viele, z. B.

$y=-2 \;\;\Rightarrow\;\; a = -2-3 \cdot (-2) = 4$
Probe:
$\begin{matrix} \text{I} & 52 \cdot 4+156 \cdot (-2) &=& 208-312 &=& -104 \cr \text{II} & -4 \cdot 4-12 \cdot (-2) &=& -16+24 &=& 8 \end{matrix}$
Für $a=4$ und $y=-2$ ergeben beide Gleichungen wahre Aussagen.

$y=0 \;\;\Rightarrow\;\; a = -2-3 \cdot 0 = -2$
Probe:
$\begin{array}{crclcc} \text{I} & 52 \cdot (-2)+156 \cdot 0 &=& -104+0 &=& -104 \cr \text{II} & -4 \cdot (-2)-12 \cdot 0 &=& 8-0 &=& 8 \end{array}$
Für $a=-2$ und $y=0$ ergeben beide Gleichungen wahre Aussagen.

$y=5 \;\;\Rightarrow\;\; a = -2-3 \cdot 5 = -17$
Probe:
$\begin{array}{crclcc} \text{I} & 52 \cdot (-17)+156 \cdot 5 &=& -884+780 &=& -104 \cr \text{II} & -4 \cdot (-17)-12 \cdot 5 &=& 68-60 &=& 8 \end{array}$
Für $a=-17$ und $y=5$ ergeben beide Gleichungen wahre Aussagen.

Und viele weitere mehr ...

8) Lösung nach dem Einsetzungsverfahren
$\begin{array}{crclllcc} \text{I} & p &=& 24q-9 \cr \text{II} & \dfrac{1}{3}p+3 &=& 8q \cr \cr\text{I in II} & \dfrac{1}{3} \left(24q-9\right)+3 &=& 8q \cr & 8q-3+3 &=& 8q&\vert - 8q \cr & 0 &=& 0q \end{array}$

Auch dieses Gleichungssystem ist offensichtlich mehrdeutig lösbar. Hier müssen wir aber im Gegensatz zu Aufgabe 7) gar nicht weiter umformen, da Gleichung I - netterweise - schon in der richtigen Form vorliegt.
Die Lösungsmenge lautet also $\mathbb{L} = \{\left(24q-9; q \right) \text{ mit }q \in \mathbb{R}\}$

9) Lösung nach dem Additionsverfahren
$\begin{array}{crclllcc} \text{I} & 6a-8b &=& 2 \cr \text{II} & -3a+12b &=& 1 & \vert \cdot 2 \cr \cr \text{I} & 6a-8b &=& 2 \cr \text{II} & -6a+24b &=& 2 \cr \cr \text{I} & 6a-8b &=& 2 \cr \text{I+II} & 16b &=& 4 & \Rightarrow b = \dfrac{1}{4} \cr \cr b=\frac{1}{4} \text{ in I} & 6a-8 \cdot \dfrac{1}{4} &=& 2 \cr & 6a -2 &=& 2 &\vert +2 \cr & 6a &=& 4 & \Rightarrow a = \dfrac{2}{3} \cr \cr & \mathbb{L} &=& \left\{\left(\dfrac{2}{3}; \dfrac{1}{4}\right)\right\} \end{array}$

10) Lösung nach dem Gleichsetzungsverfahren
$\begin{array}{crclllcc}\text{I} & \dfrac{1}{16}s+t &=& -12 &\vert -t \cr \cr \text{II} & \dfrac{1}{16}s-\dfrac{3}{2}t &=& 23 &\vert +\dfrac{3}{2}t \cr \cr \cr \text{I} & \dfrac{1}{16}s&=& -12-t \cr \cr \text{II} & \dfrac{1}{16}s &=& 23+\dfrac{3}{2}t \cr \cr \cr \text{I = II} & -12-t &=& 23+\dfrac{3}{2}t &\vert -\dfrac{3}{2}t+12 \cr \cr & -t-\dfrac{3}{2}t &=& 23+12 \cr \cr & -\dfrac{5}{2}t &=& 35 & \Rightarrow t=-14 \cr \cr \cr t=-14 \text{ in I} & \dfrac{1}{16}s-14 &=& -12 &\vert +14 \cr \cr & \dfrac{1}{16}s &=& 2 & \Rightarrow s = 32 \cr \cr \cr & \mathbb{L} &=& \{\left(32; -14\right)\} \end{array}$

2. Aufgabe

Sei $h$ die Anzahl der Hühner und $s$ die Anzahl der Schweine (siehe Bemerkung zu Textaufgaben).

Dann gilt:
I $h+s=37$
Denn jedes der Tiere hat genau einen Kopf.
II $2h+4s=90$
Denn jedes Huhn hat $2$ Beine, also haben $h$ Hühner zusammen $2h$ Beine. Schweine haben $4$ Beine, also haben $s$ Schweine $4s$ Beine. Zusammen haben alle Tiere folglich $2h+4s$ Beine.

Rechnerische Lösung (Additionsverfahren):
Zu lösen ist also das folgende lineare Gleichungssystem:
$\begin{array}{crclllcc} \text{I} & h+s &=& 37 & \vert \cdot (-2) \cr \text{II} & 2h+4s &=& 90 \cr \cr \text{I} & -2h-2s &=& -74 \cr \text{II} & 2h+4s &=& 90 \cr \cr \text{I} & -2h-2s &=& -74 \cr \text{I+II} & 2s &=& 16 & \Rightarrow s = 8 \cr \cr s = 8 \text{ in I} & h+8 &=& 37 & \Rightarrow h = 29 \end{array}$

Herr Müller hat $29$ Hühner und $8$ Schweine.


Zeichnerische Lösung:
Man formt die Gleichungen I und II von oben so um, dass sie der allgemeinen Geradengleichung entsprechen, nämlich:
I $h+s=37 \quad \Rightarrow \quad f_1(h)=s=37-h$

II $2h+4s=90 \quad \Rightarrow \quad f_2(h)=s=\dfrac{45}{2}-\dfrac{1}{2}h$

Diese beiden Geraden können dann in ein Koordinatensystem eingetragen und der Schnittpunkt abgelesen werden.

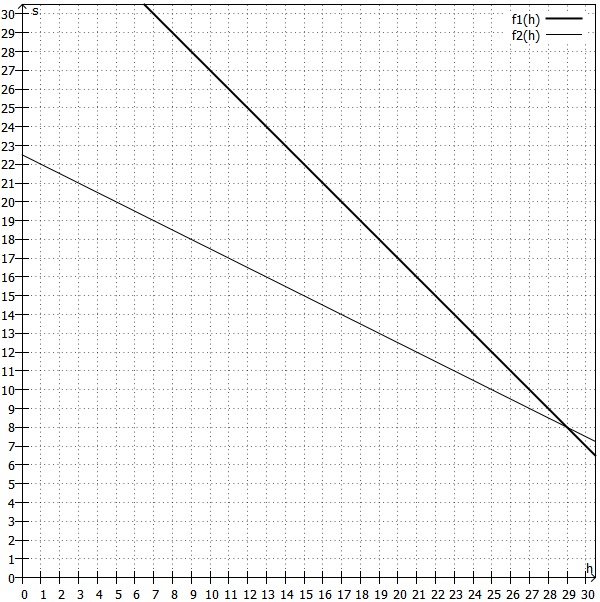
Der Schnittpunkt der beiden Geraden liegt bei $S(29 \mid 8)$. $h$, also die Anzahl der Hühner, ist $29$ und $s$, also die Anzahl der Schweine, ist $8$. Jedes andere Ergebnis hätte uns stutzig machen sollen ...

Da in diesem Zusammenhang offensichtlicherweise nur ganzzahlige Lösungen sinnvoll sind, ist die folgende Grafik, in der keine Geraden, sondern einzelne Punkte an den entsprechenden Stellen eingezeichnet wurden, besser:

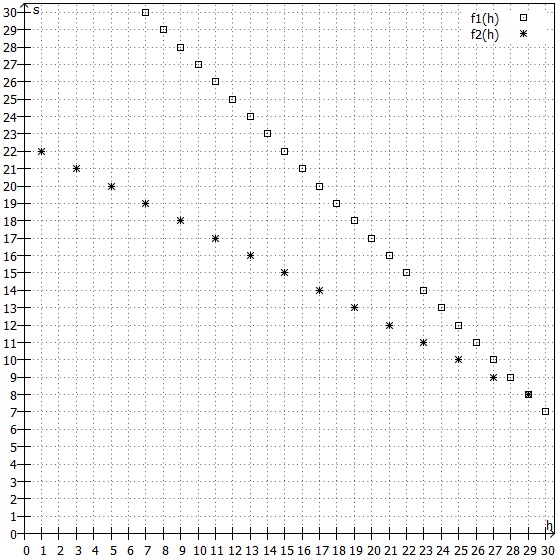
3. Aufgabe

Sei $b$ die Anzahl der billigen Schokoladentäfelchen und $t$ die Anzahl der teuren Schokoladentäfelchen (siehe Bemerkung zu Textaufgaben).
Eine billige Schokolade kostet laut Aufgabenstellung $0{,}06$ EUR, eine teure $0{,}14$ EUR.

a)
Es gilt: $0{,}06b + 0{,}14t = 11{,}20$
Der Preis für eine billigen Schokolade mal die Anzahl der billigen Schokoladentafeln plus den Preis für eine teure Schokolade mal die Anzahl der teuren Tafeln ergibt den Gesamtpreis.

Mögliche Ergebnisse $(b; t)$ sind also: $(0; 80)$, $(7; 77)$, $(14; 74)$, $(21; 71)$,…, $(161; 11)$, $(168; 8)$, $(175; 5)$, $(182; 2)$
Denn $0{,}06 \cdot 0+0{,}14 \cdot 80 = 11{,}20$ usw. Das findet man "einfach" durch Einsetzen und Ausprobieren heraus.

Bitte achten Sie darauf, dass hier nur ganzzahlige Angaben infrage kommen!
 
b)
Zur oberen Gleichung kommt dazu: $b+t = 100$
Denn die Gesamtzahl der Schokoladentäfelchen soll $100$ betragen.

Es ergibt sich das folgende lineare Gleichungssystem, das mit dem Einsetzungsverfahren gelöst wird:
$\begin{array}{crclcl} \text{I} & 0{,}06b+0{,}14t &=& 11{,}20 \cr \text{II} & b+t &=& 100 &\vert& -t \cr \cr \text{I} & 0{,}06b+0{,}14t &=& 11{,}20 \cr \text{II} & b &=& 100-t \cr \cr \text{II in I} & 0{,}06 \cdot (100-t)+0{,}14t &=&11{,}20 \cr & 6-0{,}06t+0{,}14t &=& 11{,}20 &\vert& -6 \cr & 0{,}08t &=& 5{,}20 &\vert& : 0{,}08 \cr & t &=& 65 \end{array}$

Es sind $65$ teure Schokoladen in der Großpackung enthalten.

Bemerkung: Da nur nach der Anzahl der teuren Schokoladentäfelchen gefragt war, kann die Bearbeitung der Aufgabe hier abgebrochen werden. Hätte das Gleichungssystem vollständig gelöst werden sollen, müsste auch für $b$ ein Wert ermittelt werden.

4. Aufgabe

1)
$\begin{array}{crcrcrcrl} \text{I} & 8x &+& 9y &-& 5z &=& -9 \cr \text{II} & -6x &-& 3y &+& 5z &=& -27 \cr \text{III} & \frac{1}{2}x &+& y &-& 2z &=& -10 \cr \cr \text{I} & 8x &+& 9y &-& 5z &=& -9 \cr \text{3 I+4 II} & & & 15y &+& 5z &=& -135 \cr \text{I-16 III} & & & -7y &+& 27z &=& 151 \cr \cr \text{I} & 8x &+& 9y &-& 5z &=& -9 \cr \text{II'} & & & 15y &+& 5z &=& -135 \cr \text{7 II'+15 III'} & & & & & 440z &=& 1320 & \Rightarrow z = 3 \cr \cr z = 3 \text{ in II'} & & & 15y &+& 5 \cdot 3 &=& -135 & \Rightarrow y = -10 \cr z = 3 \text{ und } y = -10 \text{ in I} & 8x &+& 9 \cdot \left(-10\right) &-& 5 \cdot 3 &=& -9 & \Rightarrow x = 12 \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \{\left(12; -10; 3\right)\}$

2)
$\begin{array}{crcrcrcrl} \text{I} & 7x &+& 5y &-& 10z &=& 12 \cr \text{II} & -28x &-& 35y &+& 16z &=& -23 \cr \text{III} & -21x &-& 30y &+& 6z &=& 9 \cr \cr \text{I} & 7x &+& 5y &-& 10z &=& 12 \cr \text{4 I+II} & & & -15y &-& 24z &=& 25 \cr \text{3I+III} & & & -15y &-& 24z &=& 45 \cr \cr \text{I} & 7x &+& 5y &-& 10z &=& 12 \cr \text{II'} & & & -15y &-& 24z &=& 25 \cr \text{II'-III'} & & & & & 0 &=& -20 \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \emptyset$

3)
$\begin{array}{crcrcrcrl} \text{I} & -\dfrac{3}{2}a &+& \dfrac{1}{7}b &+& c &=& 6 \cr \cr \text{II} & \dfrac{5}{6}a &+& \dfrac{1}{3}b &-& \dfrac{1}{3}c &=& 2 \cr \cr \text{III} & & & -\dfrac{4}{3}b &-& \dfrac{5}{3}c &=& -3 \cr \cr \cr \text{14 I} & -21a &+& 2b &+& 14c &=& 84 \cr \text{6 II} & 5a &+& 2b &-& 2c &=& 12 \cr \text{3 III} & & & -4b &-& 5c &=& -9 \cr \cr \text{I} & -21a &+& 2b &+& 14c &=& 84 \cr \text{5 I+21 II} & & & 52b &+& 28c &=& 672 \cr \text{III} & & & -4b &-& 5c &=& -9 \cr \cr \text{I} & -21a &+& 2b &+& 14c &=& 84 \cr \text{II'} & & & 52b &+& 28c &=& 672 \cr \text{II'+13 III'} & & & & & -37c &=& 555 & \Rightarrow c = -15 \cr \cr c = -15 \text{ in II'} & & & 52b &+& 28 \cdot \left(-15\right) &=& 672 & \Rightarrow b = 21 \cr c = -15 \text{ und } b = 21 \text{ in I} & -21a &+& 2 \cdot 21 &+& 14 \cdot \left(-15\right) &=& 84 & \Rightarrow a = -12 \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \{\left(-12; 21; -15\right)\}$

Bemerkung: Die ersten Umformungen (Multiplikation jeweils mit dem Hauptnenner) wurden durchgeführt, damit in der Folgerechnung keine Brüche mehr auftauchen. Allerdings werden dadurch die Zahlenwerte natürlich größer ...

4)
$\begin{array}{crcrcrcrl} \text{I} & -18x &-& 4y &-& 26z &=& 4 \cr \text{II} & 9x &+& 8y &+& 13z &=& -5 \cr \text{III} & 9x &-& 12y &+& 7z &=& 11 \cr \cr \text{I} & -18x &-& 4y &-& 26z &=& 4 \cr \text{I+2 II} & & & 12y & & &=& -6 & \Rightarrow y = -\dfrac{1}{2} \cr \text{I+2 III} & & & -28y &-& 12z &=& 26 \cr \cr \cr y =-\frac{1}{2} \text{ in III'} & & & -28\cdot \left(-\dfrac{1}{2}\right) &-& 12z &=& 26 & \Rightarrow z = -1 \cr \cr y =-\frac{1}{2} \text{ und }z = -1 \text{ in I} & -18x &-& 4 \cdot \left(-\dfrac{1}{2}\right) &-& 26 \cdot \left(-1\right) &=& 4 & \Rightarrow x = \dfrac{4}{3} \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \left\{\left(\dfrac{4}{3}; -\dfrac{1}{2}; -1\right)\right\}$

5)
$\begin{array}{crcrcrcrl} \text{I} & 11a &-& 8b &+& c &=& 37 \cr \text{II} & -a &-& 2b &+& 7c &=& -35 \cr \text{III} & 12a &+& 9b &-& 6c &=& 12 \cr \cr \text{II} & -a &-& 2b &+& 7c &=& -35 \cr \text{I} & 11a &-& 8b &+& c &=& 37 \cr \text{III} & 12a &+& 9b &-& 6c &=& 12 \cr \cr \text{II} & -a &-& 2b &+& 7c &=& -35 \cr \text{11 II+I} & & & -30b &+& 78c &=& -348 \cr \text{12 II+III} & & & -15b &+& 78c &=& -408 \cr \cr \text{II} & -a &-& 2b &+& 7c &=& -35 \cr \text{I'} & & & -30b &+& 78c &=& -348\cr \text{I'-2 III'} & & & & & -78c &=& 468 & \Rightarrow c = -6 \cr \cr c = -6 \text{ in I'} & & & -30b &+& 78\cdot \left(-6\right) &=& -348 & \Rightarrow b = -4 \cr c = -6 \text{ und } b = -3 \text{ in II} & -a &-& 2\cdot \left(-4\right) &+& 7\cdot \left(-6\right) &=& -35 & \Rightarrow a = 1 \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \{\left(1; -4; -6\right)\}$

Bemerkung: Im ersten Schritt wurden nur die ersten beiden Gleichungen vertauscht (Sie sehen das an der Nummerierung der Gleichungen.), da die weiteren Umformungen mit dem Koeffizienten $-1$ wie in Gleichung $\text{II}$ einfacher durchzuführen sind.

6)
$\begin{array}{crcrcrcrl} \text{I} & 4x &+& 2y &-& z &=& 1 \cr \text{II} & -8x &-& 6y &+& 8z &=& -13 \cr \text{III} & -4x &+& 10y &-& 5z &=& 9 \cr \cr \text{I} & 4x &+& 2y &-& z &=& 1 \cr \text{2I+II} & & & -2y &+& 6z &=& -11 \cr \text{I+III} & & & 12y &-& 6z &=& 10 \cr \cr \text{I} & 4x &+& 2y &-& z &=& 1 \cr \text{II'} & & & -2y &+& 6z &=& -11 \cr \text{II'+III'} & & & 10y & & &=& -1 & \Rightarrow y = -\dfrac{1}{10} \cr \cr \cr y = -\frac{1}{10} \text{ in II'} & & & -2\cdot \left( -\dfrac{1}{10} \right) &+& 6z &=& -1 & \Rightarrow z = -\dfrac{28}{15} \cr \cr y = -\frac{1}{10} \text{ und } z = -\frac{28}{15} \text{ in I} & 4x &+& 2\cdot \left( -\dfrac{1}{10} \right) &-& \left(-\dfrac{28}{15}\right) &=& 1 & \Rightarrow x = -\dfrac{1}{6} \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \left\{\left(-\dfrac{1}{6}; -\dfrac{1}{10}; -\dfrac{28}{15}\right)\right\}$

7)
$\begin{array}{crcrcrcrl} \text{I} & 7x &-& 5y &+& 2z &=& 16 \cr \text{II} & 14x &-& 7y & & &=& 14 \cr \text{III} & -3x & & &-& z &=& -3 \cr \cr \text{I} & 7x &-& 5y &+& 2z &=& 16 \cr \text{II} & 14x &-& 7y & & &=& 14 \cr \text{I+2III} & x &-& 5y & & &=& 10 \cr \cr \text{I} & 7x &-& 5y &+& 2z &=& 16 \cr \text{II} & x &-& 5y & & &=& 10 \cr \text{II-14III'} & & & 63y & & &=& -126 & \Rightarrow y = -2 \cr \cr y = -2 \text{ in II} & & & x &-& 5\cdot \left(-2\right) &=& 10 & \Rightarrow x = 0 \cr x = 0 \text{ und } y = -2 \text{ in I} & 7\cdot0 &-& 5\cdot \left(-2\right) &+& 2z &=& 16 & \Rightarrow z = 3 \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \{\left(0; -2; 3\right)\}$

8)
$\begin{array}{crcrcrcrl} \text{I} & 2r &+& 2s &+& 3t &=& 7 \cr \text{II} & & & -4s &-& 4t &=& 5 \cr \text{III} & 4r &+& 8s &+& 10t &=& 6 \cr \cr \text{I} & 2r &+& 2s &+& 3t &=& 7 \cr \text{II} & & & -4s &-& 4t &=& 5 \cr \text{2I-III} & & & -4s &-& 4t &=& 8 \cr \cr \text{I} & 2r &+& 2s &+& 3t &=& 7 \cr \text{II} & & & 4s &+& 4t &=& 5 \cr \text{II-III'} & & & & & 0 &=& -3 \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \emptyset$

9)
$\begin{array}{crcrcrcrl} \text{I} & 4x &+& 5y &-& 8z &=& 21 \cr \text{II} & -2x &+& 3y &-& 6z &=& -17 \cr \text{III} & 2x &+& 8y &-& 14z &=& 4 \cr \cr \text{I} & 4x &+& 5y &-& 8z &=& 21 \cr \text{I+2II} & & & 11y &-& 20z &=& -13 \cr \text{II+III} & & & 11y &-& 20z &=& -13 \cr \cr \text{I} & 4x &+& 5y &-& 8z &=& 21 \cr \text{II'} & & & 11y &-& 20z &=& -13 \cr \text{II'-III'} & & & 0y &+& 0z &=& 0 & \end{array}$

Die Gleichung II'+III' ergibt für alle reellen Zahlen $y$ und $z$ eine wahre Aussage. Die Lösung dieses linearen Gleichungssystems hängt also nur von den Gleichungen I und II' ab. Da diese beiden linearen Gleichungen allerdings drei Variablen haben, bekommen wir keine eindeutige Lösung. Wir müssen so tun, als wäre eine Variable aus der Gleichung II' (das ist die, die nur noch zwei Variablen enthält) fix. Wir nehmen hier mal hier mal an, dass $z$ als reelle Zahl festgelegt wäre (mit $y$ würde es aber genauso funktionieren). $z$ wird damit zu einem sogenannten Parameter. Dann können wir Gleichung II' so umformen, dass $y$ alleine auf einer Seite steht:

$\begin{array}{crcrcrcl} \text{II'} & 11y &-& 20z &=& -13 & \vert & +20z \cr & 11y & & &=& -13+20z & \vert & :11 \cr\cr&&& y &=& -\dfrac{13}{11}+\dfrac{20}{11}z \end{array}$

Damit wissen wir, wie sich $y$ berechnet lässt, vorausgesetzt wir haben einen Wert für $z$. Bleibt die Frage, was mit $x$ ist. Dafür nehmen wir die dritte Gleichung dieses Gleichungssystems, also Gleichung I, und setzten $y = -\frac{13}{11}+\frac{20}{11}z$ und $z$ ein:

$\begin{array}{rcrcrcrcrl} \text{I} & 4x &+& 5y &-& 8z &=& 21 \cr \cr & 4x &+& 5\left(-\dfrac{13}{11}+\dfrac{20}{11}z\right) &-& 8z &=& 21 \cr \cr &4x &-& \dfrac{65}{11}+\dfrac{100}{11}z &-& 8z &=& 21 & \vert &+\dfrac{65}{11} \cr \cr & 4x & & &+& \dfrac{12}{11}z &=& 21+\dfrac{65}{11} & \vert & -\dfrac{12}{11}z \cr \cr & 4x& & & & &=& \dfrac{296}{11}-\dfrac{12}{11}z & \vert & :4 \cr \cr & & & & & x &=& \dfrac{74}{11}-\dfrac{3}{11}z & \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \left\{\left(\dfrac{74}{11}-\dfrac{3}{11}z; -\dfrac{13}{11}+\dfrac{20}{11}z; z\right) \text{ mit } z \in \mathbb{R} \right\}$

10)
$\begin{array}{crcrcrcrl} \text{I} & 3x_1 &-& 6x_2 &+& 9x_3 &=& 21 \cr \text{II} & -x_1 &+& 2x_2 &+& 4x_3 &=& 21 \cr \text{III} & -x_1 & & &+& 5x_3 &=& 21 \cr \cr \text{I} & 3x_1 &-& 6x_2 &+& 9x_3 &=& 21 \cr \text{I + 3II} & & & & & 21x_3 &=& 84 &\Rightarrow x_3=4 \cr \text{III} & -x_1 & & &+& 5x_3 &=& 21 \cr\cr x_3=4 \text{ in III} & -x_1 & & &+& 5\cdot 1 &=& 21 &\Rightarrow x_1=-1 \cr x_1=-1 \text{ und } x_3=4 \text{ in I} & 3\cdot (-1) &-& 6 \cdot x_2 &+& 9\cdot 4 &=& 21 &\Rightarrow x_2=2 \end{array}$

Die Lösungsmenge lautet also $\mathbb{L} = \{\left(-1; 2; 4\right)\}$