Lernmodul Mathematik

Übersicht:

10.1 Quadratische Funktionen - Aufgaben

1. Aufgabe

Zeichnen Sie eine Normalparabel, d. h. die Funktion $f(x)=x^2$ , in ein Koordinatensystem!

Skizzieren Sie - ausgehend von diesem Graphen - die Graphen zu folgenden Funktionen! Gemeint ist diese Aufgabe so, dass Sie überlegen, wie die Funktionen sich von der Normalparabel unterscheiden und daraus ableiten, wie der Graph aussehen muss. Eine ausführliche Wertetabelle ist nicht nötig.

1) $f_1(x) = x^2+4$		5) $f_5(x) = 4 x^2$
2) $f_2(x) = x^2-4$		6) $f_6(x) = -4x^2$
3) $f_3(x) = (x+4)^2$		7) $f_7(x) = \dfrac{1}{4}x^2$
4) $f_4(x) = (x-4)^2$		8) $f_8(x) = -\dfrac{1}{4}x^2$

Skizzieren Sie auch die folgenden Graphen in einem Koordinatensystem - auch hier nicht über eine Wertetabelle, sondern über Überlegungen zum Scheitelpunkt und zur Streckung/Stauchung.

1) $f_1(x) = \dfrac{1}{2}x^2-12$		6) $f_6(x) = x^2-8$
2) $f_2(x) = -2(x-3)^2$		7) $f_7(x) = -\dfrac{7}{13}(x-9)^2$
3) $f_3(x) = (x-5)^2+5$		8) $f_8(x) = -(x+6)^2+4$
4) $f_4(x) = \dfrac{10}{3} \left(x+10 \right)^2+2$		9) $f_9(x) = -x^2+2$
5) $f_5(x) = \left(x+\dfrac{1}{2}\right)^2-4$		10) $f_{10}(x) = (x-3{,}5)^2$

2. Aufgabe

Beantworten Sie zu den quadratischen Funktionen jeweils die folgenden Fragen:

Wie viele Nullstellen hat die Funktion?
Ist die Parabel nach oben oder nach unten geöffnet?
Ist die Parabel symmetrisch zur y-Achse oder zu einer Parallelen der y-Achse?
Ist der Funktionsgraph steiler als, weniger steil als oder genauso steil wie eine Normalparabel?

Und das Alles: Ohne zu rechnen! Es geht nämlich bei dieser Aufgabe darum, den Funktionsterm zu verstehen und daraus Informationen über den Funktionsgraphen abzulesen, um z. B. Rechnungen plausibilisieren zu können.

1) $g(x)=-x^2+6$		11) $s(t)=-\dfrac{2}{3}t^2-\dfrac{2}{3}$
2) $h(x)=26x^2-13x+5$		12) $f(x)=(x+2)^2$
3) $f(x)=-5x^2-2x$		13) $u(x)=17(518+x)(x-96)$
4) $f(x)=30(x+5)(x-10)$		14) $v(x)=\left(-\dfrac{1}{2}x-2\right)^2$
5) $f(z)=-\dfrac{1}{25}z^2$		15) $f(x)=-\dfrac{2}{3}x^2-\dfrac{2}{3}x-\dfrac{2}{3}$
6) $f(x)=-\dfrac{1}{2}x^2+\dfrac{1}{4}x-\dfrac{1}{3}$		16) $y(x)=5x^2+50x-500$
7) $f(x)=\dfrac{1}{2}x^2+2$		17) $z(x)=-22x^2-12x+2$
8) $f(x)=x^2+2x-3$		18) $f(x)=-(25x-201)^2$
9) $f(x)=\dfrac{1}{3}x^2-\dfrac{1}{9}x$		19) $f(x)=x^2+4\pi x+\pi$
10) $f(x)=-x^2+\dfrac{4}{5}x-1$		20) $f(x)=-\sqrt{2}x^2-\sqrt{112}$

3. Aufgabe

Bestimmen Sie zu den eingezeichneten Graphen jeweils die Funktionsgleichung! Es sind quadratische Funktionen gesucht.

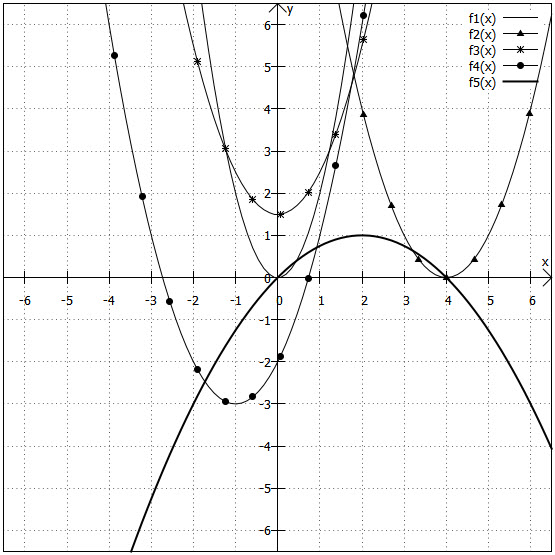4. Aufgabe

1) Gegeben sei die Funktion $f(x)=7x^2-14x+49$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=7$ b) wenn $y=105$		6) Gegeben sei die Funktion $f(x)=2(x-1)^2-\dfrac{4}{3}$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=17$ b) wenn $y=-\dfrac{4}{3}$
2) Gegeben sei die Funktion $f(x)=-x^2-24x+2$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=-11{,}5$ b) wenn $y=25$		7) Gegeben sei die Funktion $f(a)=(-3+a)^2-6$ mit $a\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(a\mid y)$ , a) wenn $a=\dfrac{15}{4}$ b) wenn $y=-43$
3) Gegeben sei die Funktion $f(x)=32x^2-x$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=8$ b) wenn $y=-4$		8) Gegeben sei die Funktion $f(x)=(4x+12)^2+8$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=5$ b) wenn $y=8$
4) Gegeben sei die Funktion $f(x)=-3x^2+7x$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=6$ b) wenn $y=4$		9) Gegeben sei die Funktion $f(x)=\dfrac{1}{10}(x-7)^2$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=18$ b) wenn $y=0$
5) Gegeben sei die Funktion $g(x)=6x^2-17$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=-\dfrac{5}{6}$ b) wenn $y=0$		10) Gegeben sei die Funktion $f(x)=100x^2-50x+25$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=\dfrac{1}{2}$ b) wenn $y=775$

5. Aufgabe

Bestimmen Sie jeweils den Scheitelpunkt der Parabel! Anders formuliert: Formen Sie die Funktionsgleichungen so um: $f(x) = a(x-d)^2+e$

1) $f(x) = x^2-6x+16$		6) $f(x)= -9x^2 - 90x - 225$
2) $f(x) = 2x^2-4x+2$		7) $f(x)= 4x^2 -4x +3$
3) $f(x) = -13x^2-8$		8) $f(x) = 3x^2-4x-\dfrac{14}{3}$
4) $f(x) = \frac{1}{4} x^2-6x+32$		9) $f(x) = \dfrac12 x^2 +4x -7$
5) $f(x) = -11x^2-44x-34$		10) $f(x) = -x^2 +26x -99$

6. Aufgabe

Stellen Sie sich eine Gerade und eine Parabel vor. Wie können diese beiden Graphen zueinander liegen und wie viele Schnittpunkte kann es zwischen ihnen geben?

Stellen Sie sich zwei Parabeln vor. Wie können diese beiden Graphen zueinander liegen und wie viele Schnittpunkte kann es zwischen ihnen geben?

7. Aufgabe

Berechnen Sie jeweils den Schnittpunkt bzw. die Schnittpunkte der folgenden zwei Funktionen!

1) $f(x) = 2x^2-4x+2$ und $g(x) = \dfrac{1}{2}x+1$		6) $f(x) = -5x^{2} + x + 2$ und $g(x) = -x^{2} + x + 1$
2) $f(x) = -9x^2+8x-1$ und $g(x) = -10x^2-\dfrac{6}{5}x+7$		7) $f(x) = -x + 4$ und $g(x) = -x^2 + 4{,}5x + 4$
3) $f(x) = \dfrac{3}{2}x^2+5x+15$ und $g(x) = x^2-x-20$		8) $f(x) = 1{,}5x^2 + 3x$ und $g(x) = 1{,}5x^2 + 10x + 14$
4) $f(x) = 4x^2-11$ und $g(x) = 12x-11$		9) $f(x) = 3x + 7$ und $g(x) = -x^2 + 10x + 1$
5) $f(x) = -3x^2-100x+300$ und $g(x) = -15x^2+20x$		10) $f(x) = \dfrac12 x^2-13x-15$ und $g(x) = -8x-15$

8. Aufgabe

Bestimmen Sie jeweils die Schnittpunkte der Funktion mit den Koordinatenachsen!

1) $f(x) = \dfrac{17}{3}\cdot (x^2-4x-221)$		6) $f(z) = -3z^2+22z-42$
2) $f(a) = -\dfrac{1}{4}a^2+a$		7) $q(t) = \left(\dfrac{t+17}{\sqrt{2}}\right)^2$
3) $h(x) = \left(x+\sqrt{2}\right)^2$		8) $f(x) = x^2+4x-5$
4) $f(x) = -\dfrac{3}{4}x^2+2$		9) $f(x) = \dfrac{a-1}{3}x^2-a$
5) $f(x) = 3x^2-6x-1$		10) $f(x) = 3x^2+(6-6r)x-12r$