Lernmodul Mathematik
Dieses Kapitel enthält die folgenden Themen:
- Ebene Figuren
- Das rechtwinklige Dreieck
- Die Satzgruppe des Pythagoras
- Winkel im Grad- und Bogenmaß
- Dreidimensionale Körper
20.2 Geometrie - Erklärungen
Die Geometrie ist ein ziemlich alter Teil der Mathematik. Schon die "alten Griechen" beschäftigten sich damit - was man bis heute an dem Begriff "euklidische Geometrie" merkt. Euklid war ein griechischer Mathematiker, der vermutlich im dritten Jahrhundert vor Christus in Alexandria lebte und die Mathematik bis in die Neuzeit hinein, u. a. durch seine Lehrbücher, entscheidend geprägt hat.
Übersetzt bedeutet Geometrie so viel wie "Vermessung der Erde". Dazu passt, dass ein wichtiger Bestandteil der Geometrie der Umgang mit Figuren in der Ebene und Körpern im Raum ist.
Ebene Figuren
Zunächst schauen wir uns die wichtigsten ebenen Figuren an und klären, mit welchen Formeln jeweils Umfang und Flächeninhalt berechnet werden können.
Dazu folgende dringende Empfehlung: Bei geometrischen Aufgaben ist immer sinnvoll, eine Skizze mit Beschriftungen anzufertigen. Das hat den Vorteil, dass man sich dadurch plastisch vor Augen führt,
- wie das gesuchte Objekt aussieht und ob die Vorstellung, die man sich "vor dem geistigen Auge" gemacht hat, mit den Angaben aus der Aufgabenstellung übereinstimmt.
Bei einem Quadrat mag es noch ganz gut ohne Skizze gehen. Bei einem Quader mit einem aufgesetzten regelmäßigen, quadratischen Pyramidenstumpf sieht das schon anders aus ... - wie die Abmessungen des Objekts sind.
Vielleicht stellt man dadurch ja fest, dass ein Dreieck gleichseitig ist ... - welche Hilfslinien ggf. gebraucht werden, um das zu berechnen/maximieren/minimieren/..., was berechnet/maximiert/minimiert/... werden soll.
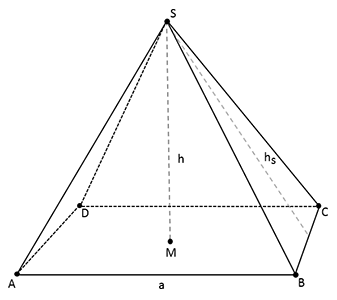
Das kann die Höhe des Quaders mit aufgesetztem Pyramidenstumpf sein, die mit der Diagonalen der Bodenfläche ein rechtwinkliges Dreieck bildet. Damit weiß man auch gleich, wie man weiterrechnen soll, nämlich mit dem Satz des Pythagoras.
Mit sehr viel Übung kann man es natürlich schaffen, sich geometrische Objekte mit allen Rahmenbedingungen so gut zu vorstellen, dass das zum Lösen der Aufgabe reicht. Wer (noch) nicht so weit ist, und das sind wohl die meisten, sollte skizzieren - immer. Eine simple Skizze kann extrem hilfreich sein und dadurch entscheidend zur richtigen Lösung der Aufgabe beitragen!
Und: Damit die Skizze ihren Nutzen erfüllen kann, muss sie so groß und ordentlich sein, dass alle relevanten Details eingetragen und gut wieder abgelesen werden können.
Vorab eine Vokabel: Sagt man, dass zwei Seiten, Diagonalen etc. "senkrecht zueinander" stehen, bedeutet dies, dass sie einen rechten Winkel einschließen.
| Eigenschaften der Figuren | Formeln | |
|---|---|---|
|
Ein Rechteck ist ein Viereck mit folgenden Eigenschaften:
|
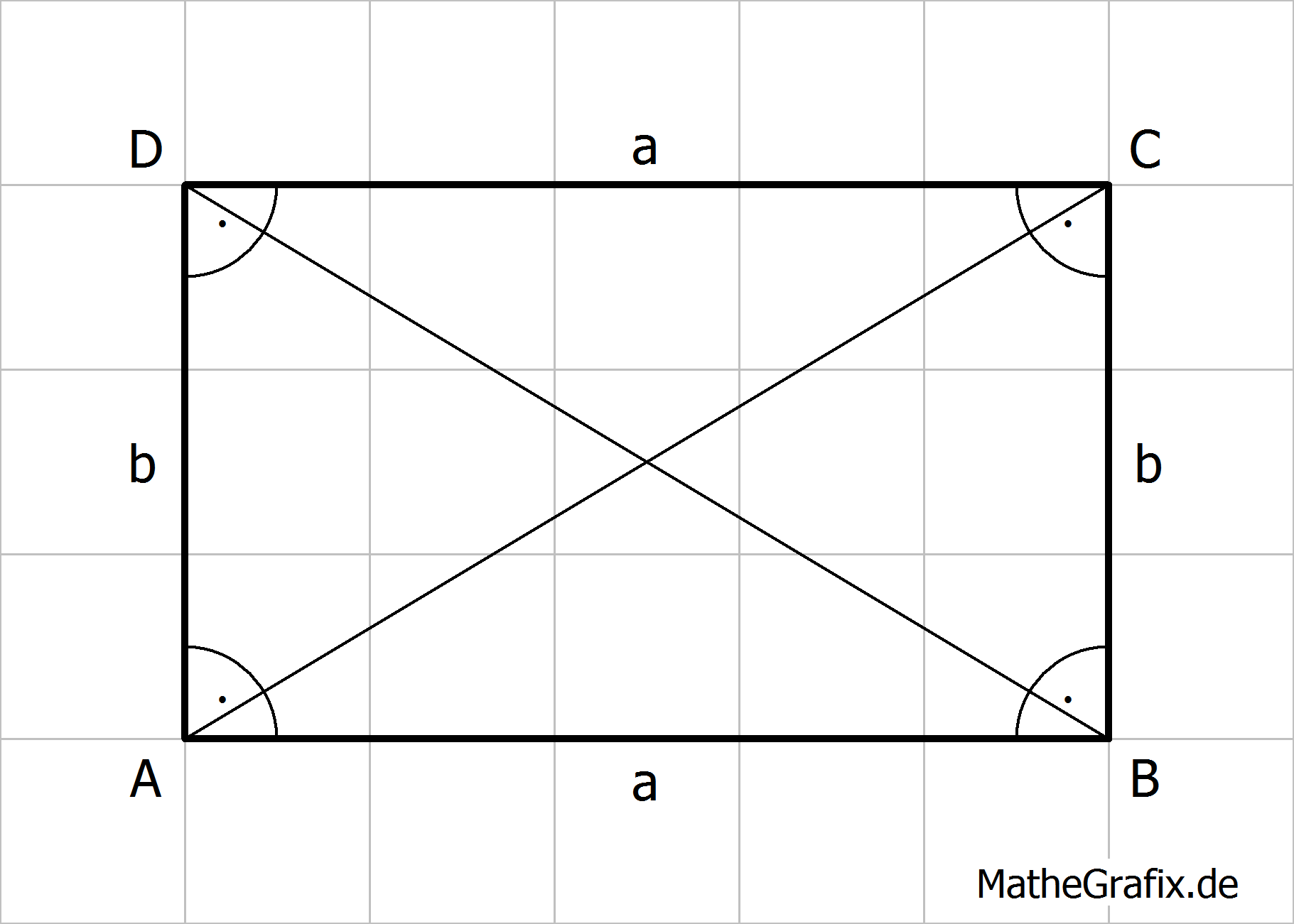 |
Flächeninhalt: Umfang: |
|
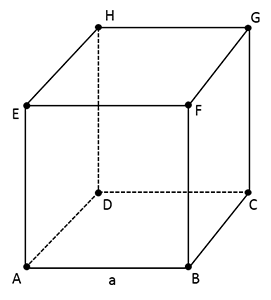
Ein Quadrat ist ein spezielles Rechteck mit folgenden Eigenschaften:
|
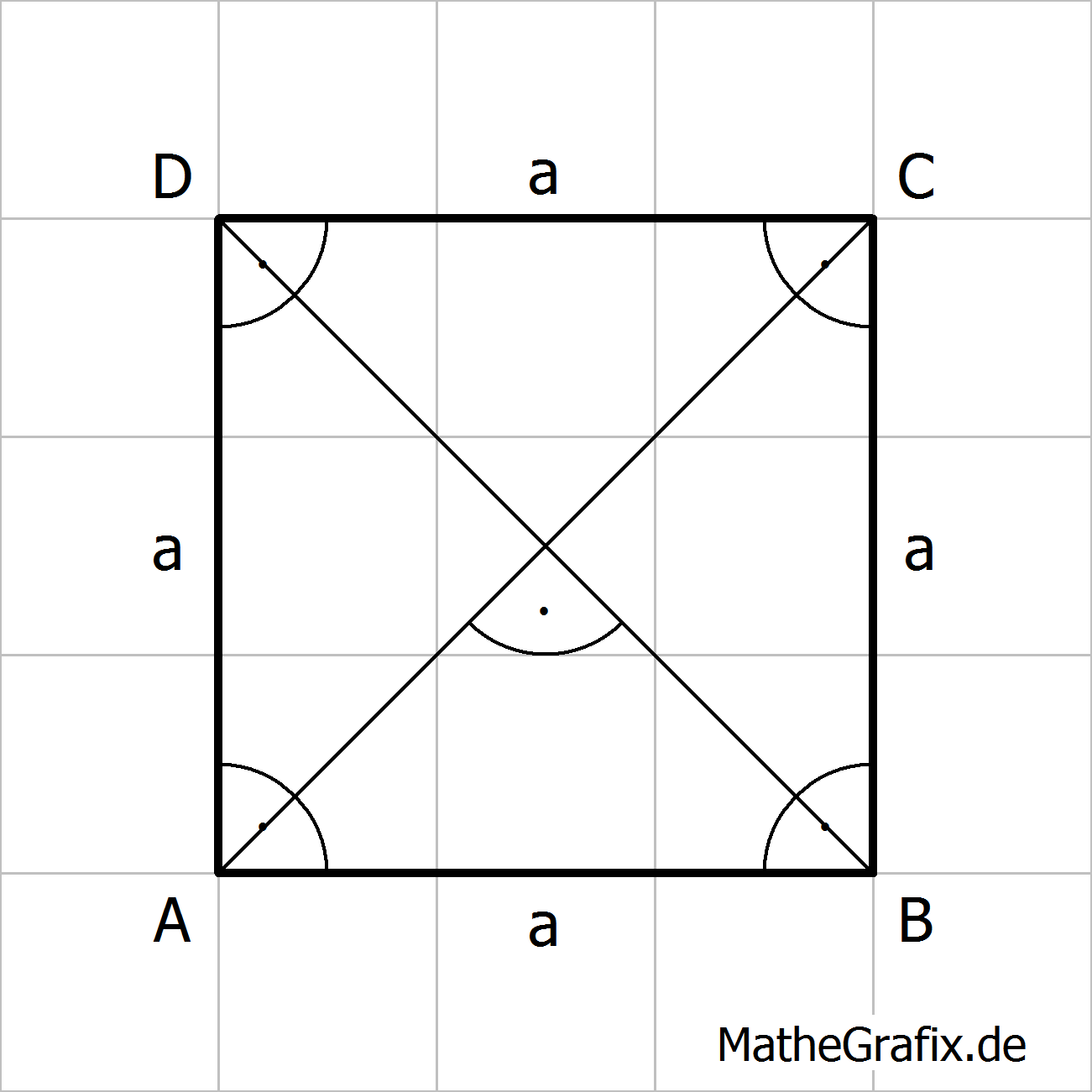 |
Flächeninhalt: Umfang: |
|
Ein Parallelogramm ist ein Viereck mit folgenden Eigenschaften:
|
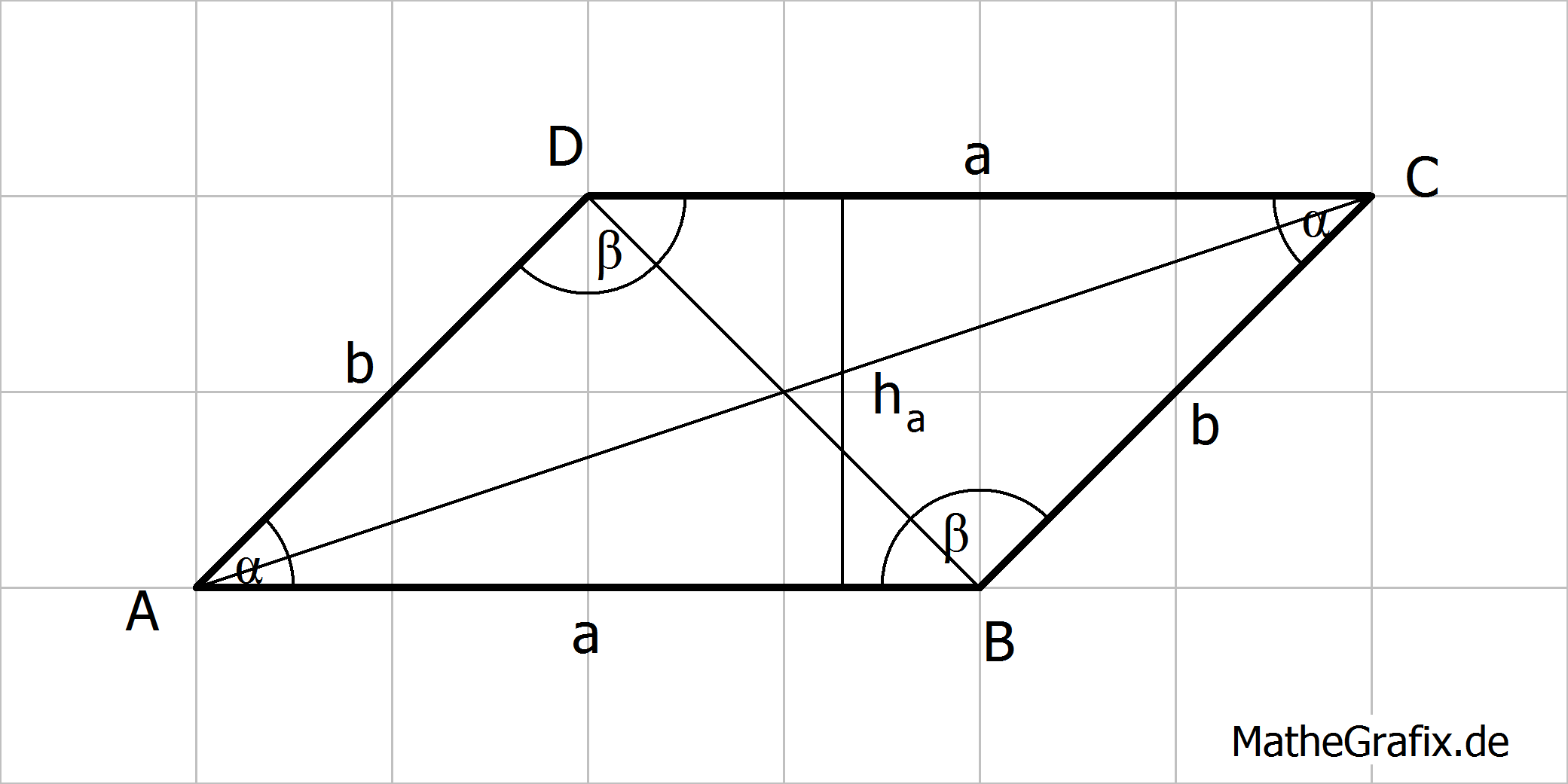 |
Flächeninhalt: Umfang: |
|
Ein/e Raute/Rhombus ist ein Viereck mit folgenden Eigenschaften:
|
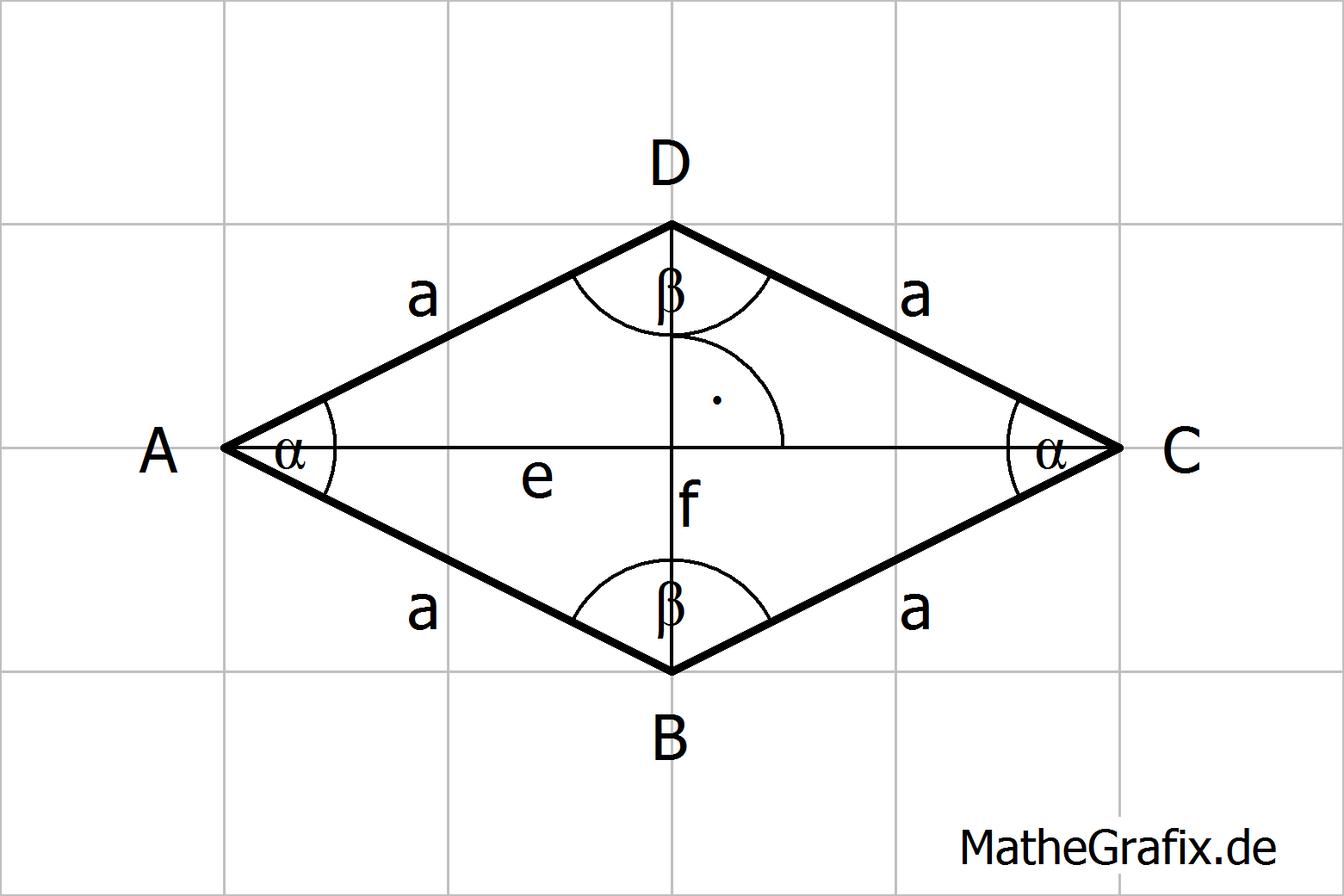 |
Flächeninhalt: Umfang: |
|
Ein Drachen/Drachenviereck ist ein Viereck mit folgenden Eigenschaften:
|
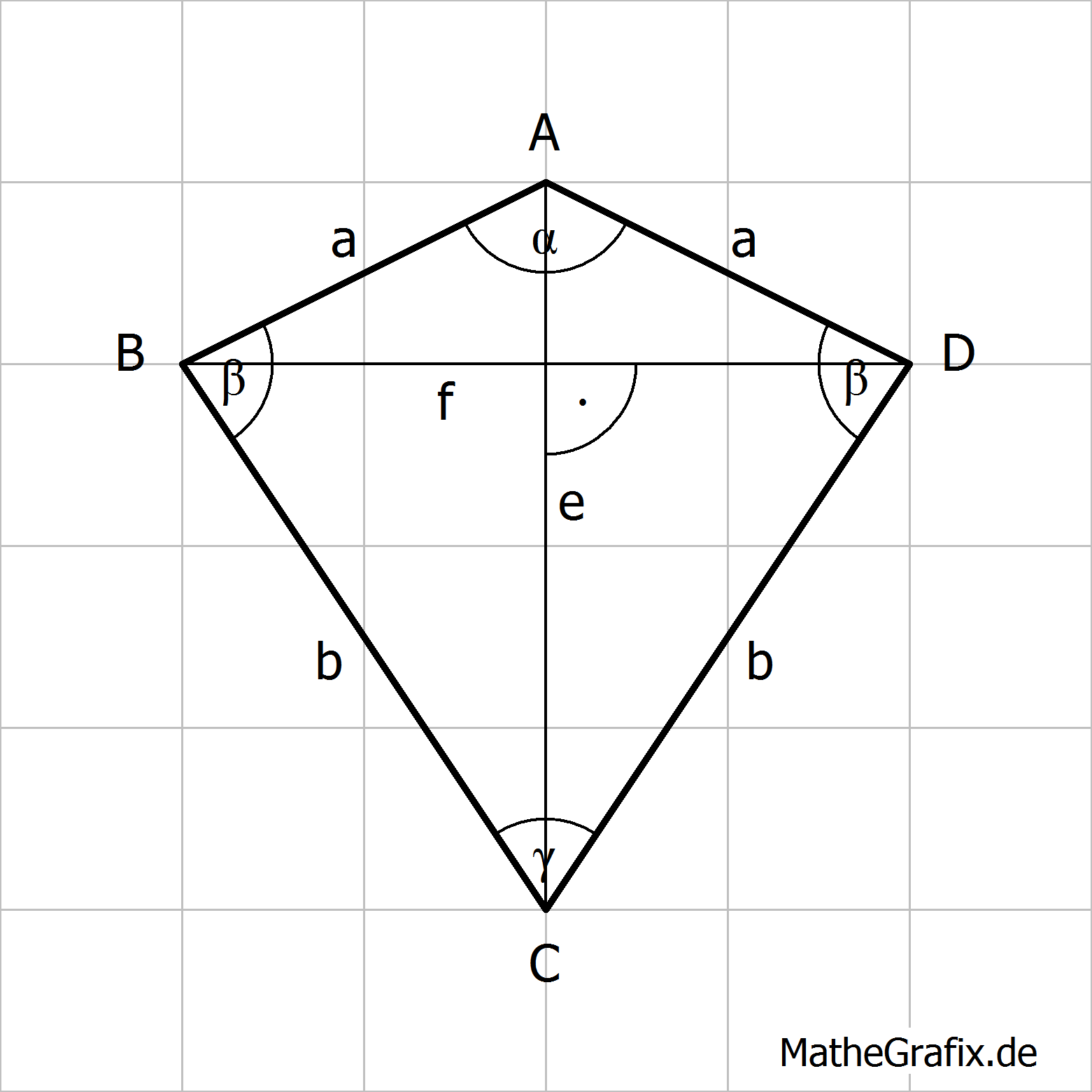 |
Flächeninhalt: Umfang: |
|
Ein Trapez ist ein Viereck mit folgender Eigenschaft:
|
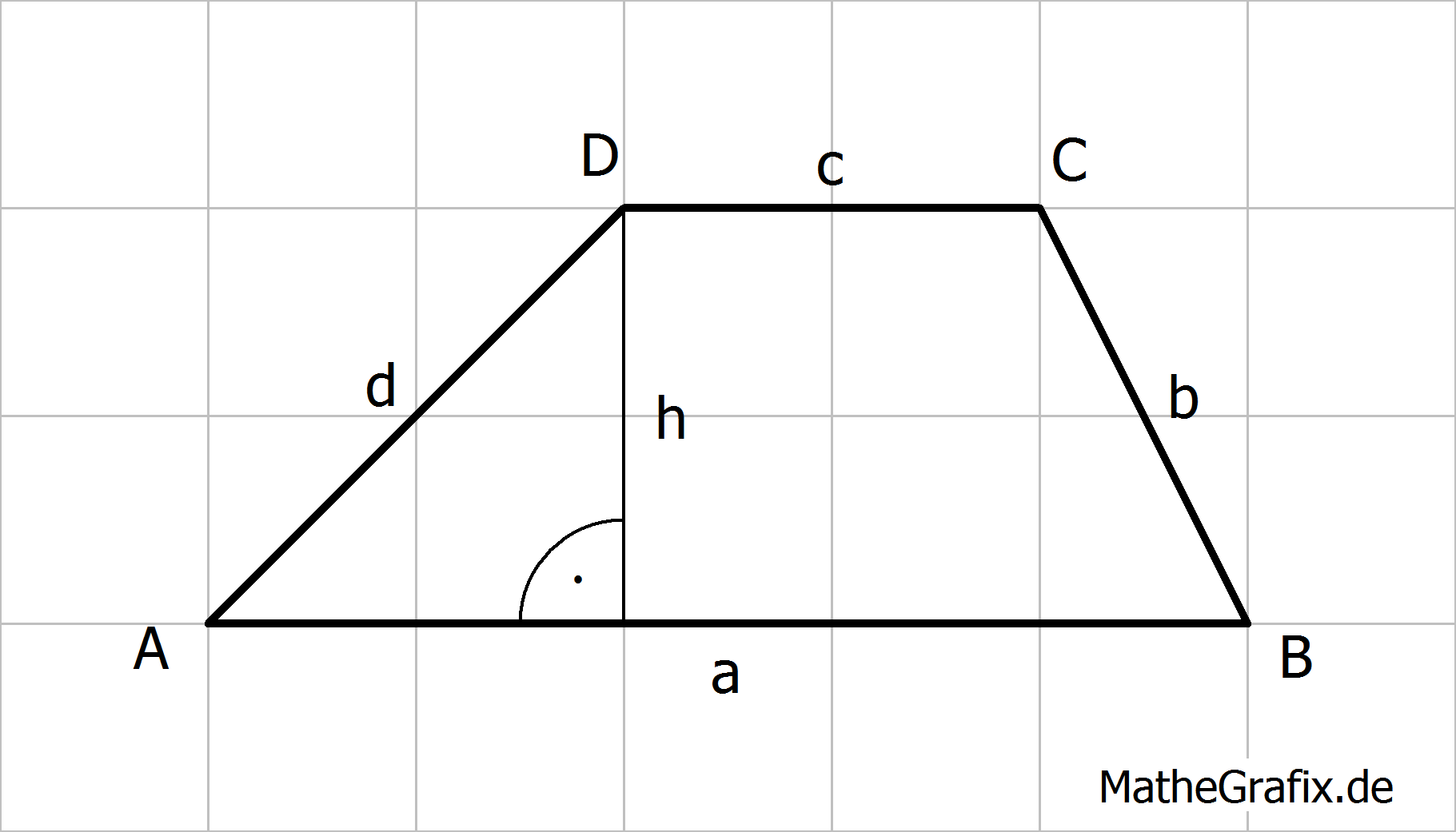 |
Flächeninhalt: Umfang: |
|
Ein gleichschenkliges Dreieck ist ein Dreieck mit folgender Eigenschaft:
|
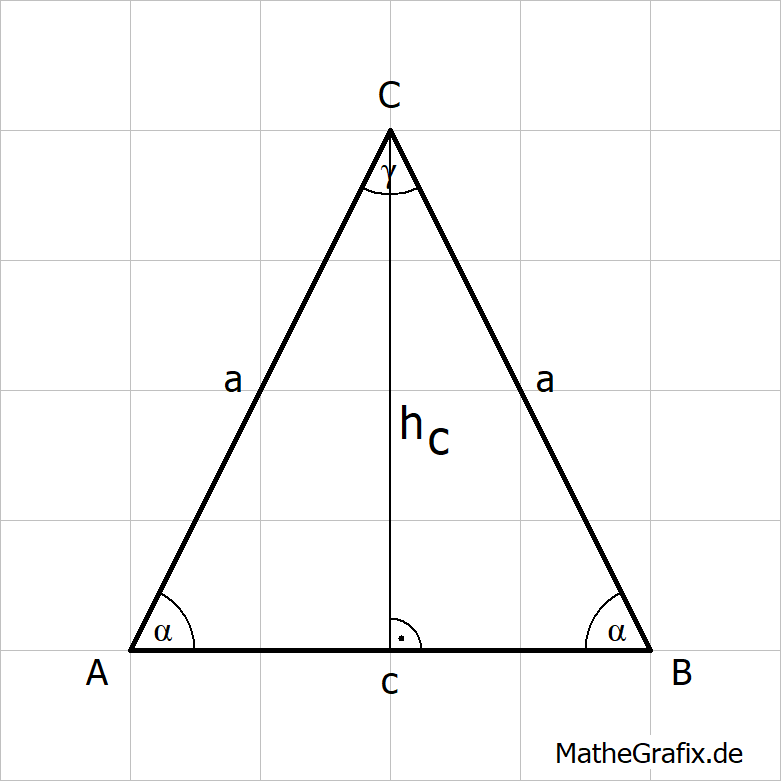 |
Flächeninhalt: Umfang: |
|
Ein gleichseitiges Dreieck ist ein spezielles gleichschenkliges Dreieck mit der folgenden Eigenschaft:
|
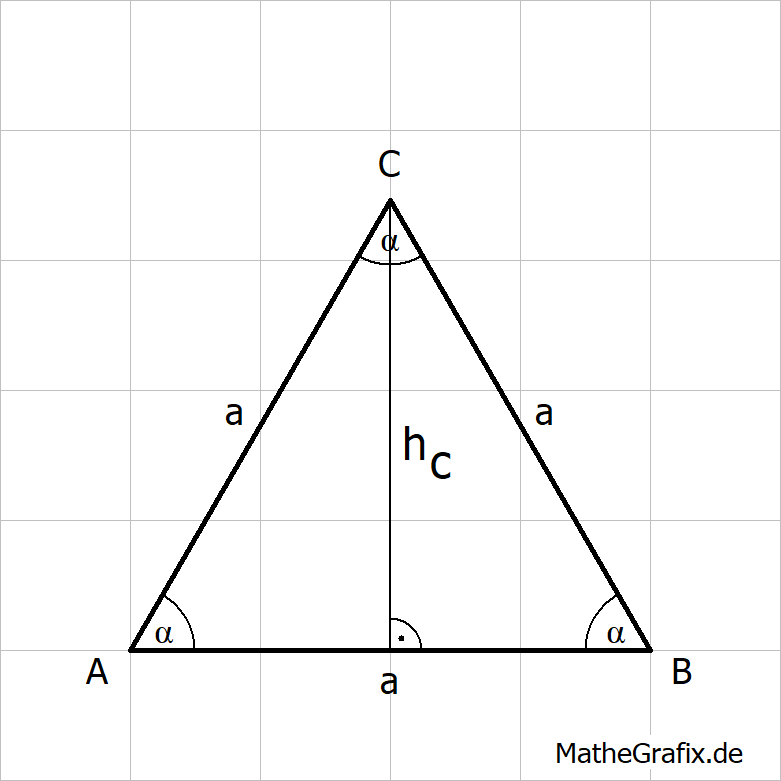 |
Flächeninhalt: Umfang: |
|
Ein rechtwinkliges Dreieck ist ein Dreieck mit folgender Eigenschaft: |
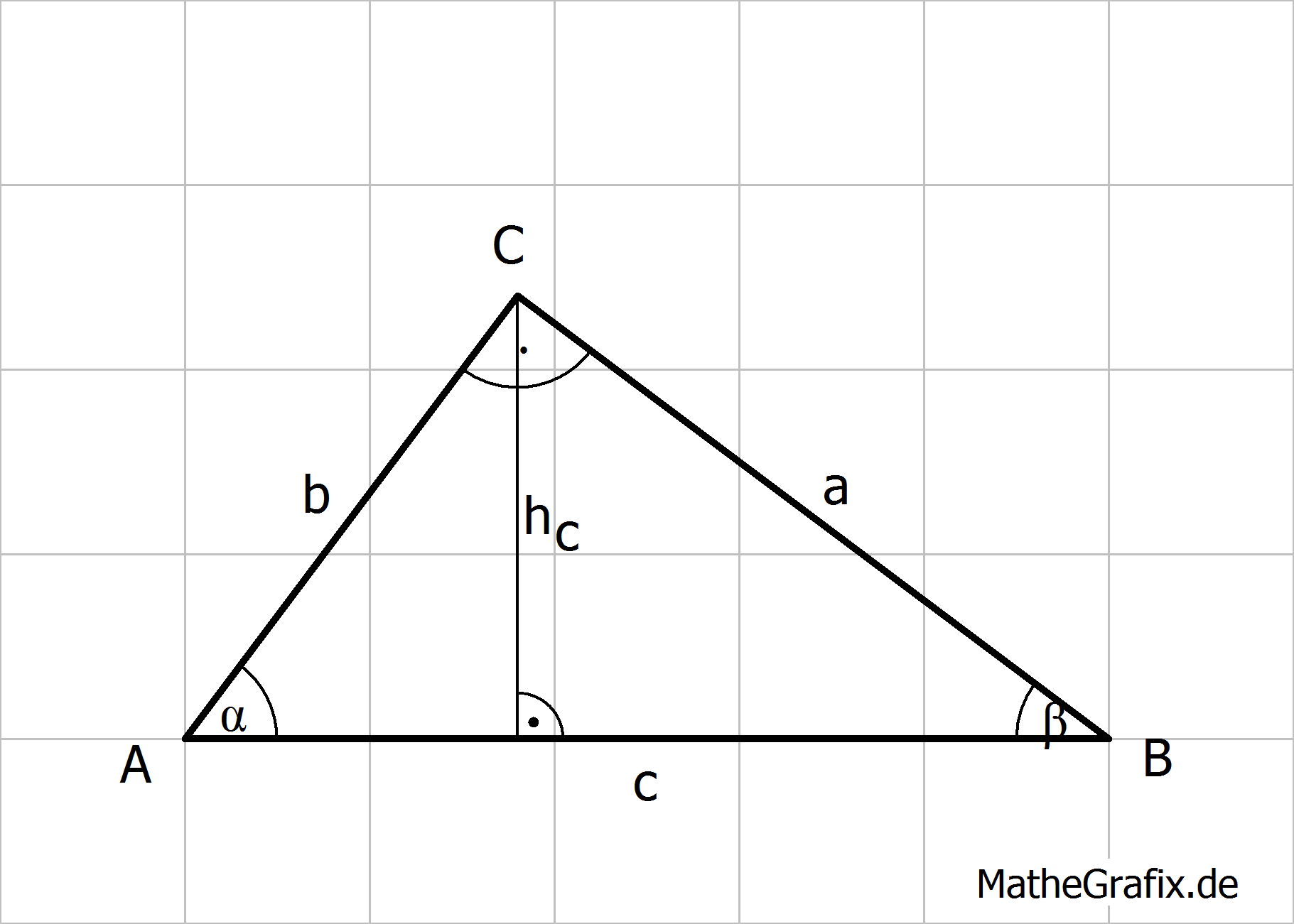 |
Flächeninhalt: Umfang: |
|
Ein Kreis hat folgende Eigenschaft:
|
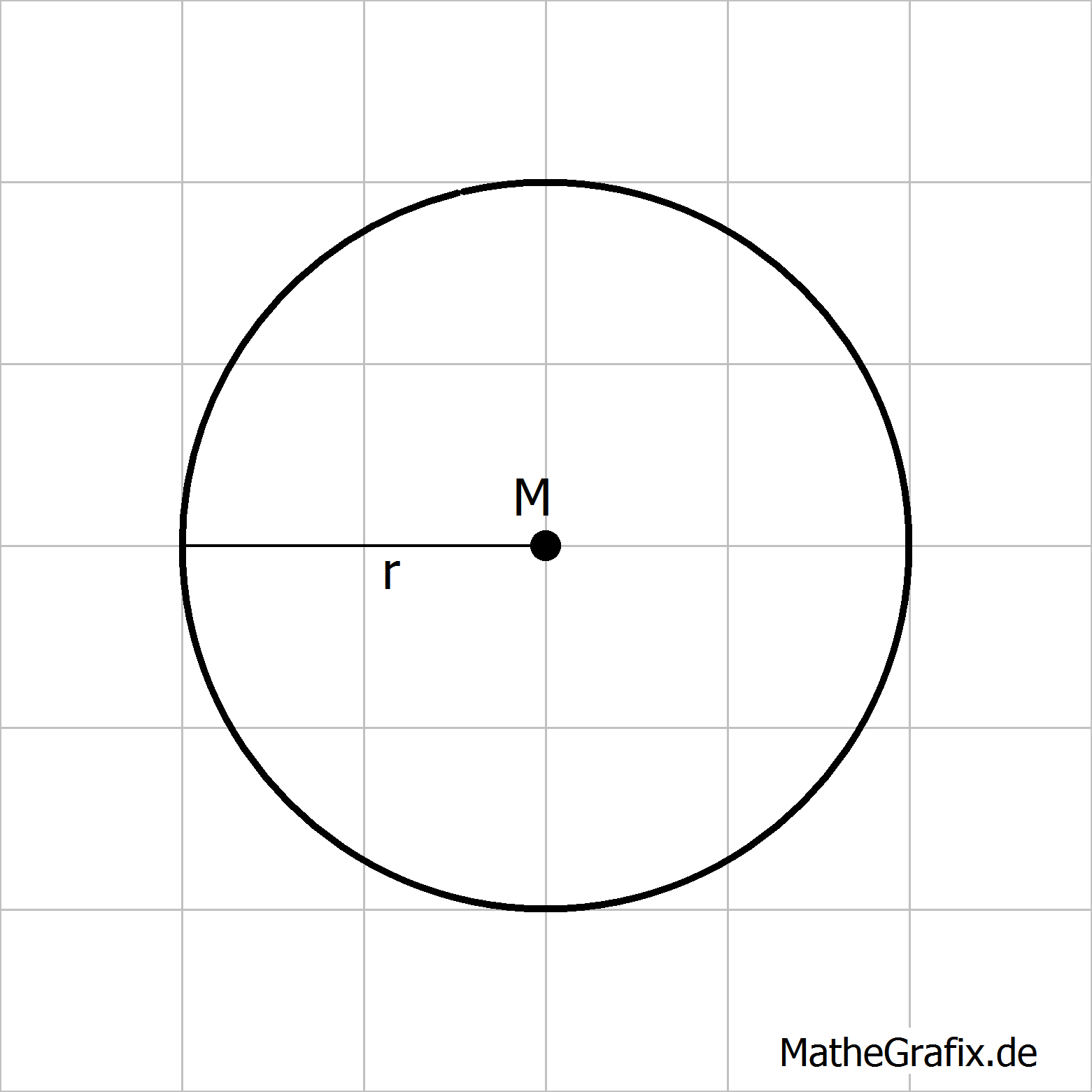 |
Flächeninhalt: Umfang: |
Das rechtwinklige Dreieck
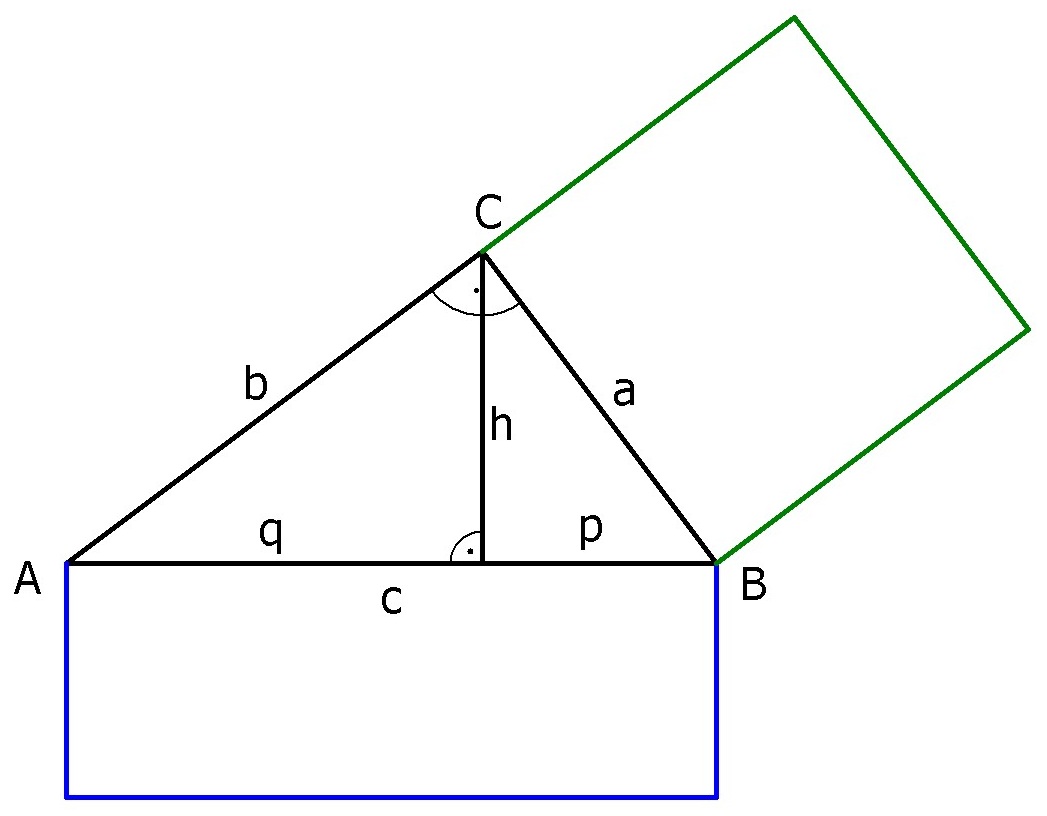
Eine besonders wichtige geometrische Figur ist das rechtwinklige Dreieck. Daher schauen wir es uns im folgenden Abschnitt etwas genauer an. Zunächst mal grafisch:
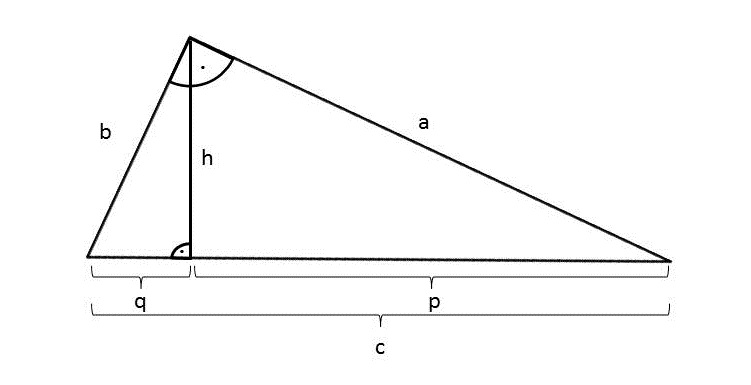
Die verschiedenen Seiten und Linien, die in der Zeichnung mit Buchstaben benannt sind, haben bestimmte Namen. Das macht es einfacher, sich über die Gegebenheiten im Dreieck zu verständigen:
Katheten: die Seiten, die an den rechten Winkel angrenzen, hier und
Hypotenuse: die Seite, die dem rechten Winkel gegenüberliegt, hier
Höhe zur Seite : die Strecke, die senkrecht auf der Dreiecksseite
steht und durch die gegenüberliegende Ecke verläuft, hier
Es gibt natürlich auch die Höhen zu den Seiten und
.
Hypotenusenabschnitte: die Teilstrecken, die durch den Schnittpunkt der Höhe mit der Hypotenuse entstehen, hier und
Wichtig sind diese Bezeichnungen auch deshalb, weil ja nicht gesagt ist, dass die Seiten links und rechts vom rechten Winkel immer und
heißen. Schauen Sie sich in der Zeichnung das Dreieck mit den Seiten
,
und
an: Es ist offensichtlich rechtwinklig, weil die Höhe ja senkrecht zur Hypotenuse stehen muss. Aber die beiden Seiten, die an den rechten Winkel angrenzen, heißen hier
und
.
Das ist vor allem auch für den nächsten Abschnitt entscheidend, denn der Satz des Pythagoras gilt natürlich auch dann, wenn die Dreieckseiten nicht ,
und
heißen ...
Die Satzgruppe des Pythagoras
Kommen wir zu einem der berühmtesten Sätze der Mathematik ... Seine Bekanntheit liegt nicht nur an seiner einfachen und gut merkbaren Form, sondern auch an seiner Geschichte. Bereits ab etwa 1800 vor Christus wurde der Zusammenhang in China und Babylon genutzt. Die "alten Ägypter" wendeten der Satzes des Pythagoras "rückwärts" an: Sie nutzen Dreiecke mit festgelegten Seitenlängen, um Felder mit rechten Winkeln anzulegen, da durch die Nilfluten regelmäßig die vorhandenen Abgrenzungen zerstört wurden.
In ebenen rechtwinkligen Dreiecken gelten die folgenden Beziehungen:
Der Satz des Pythagoras
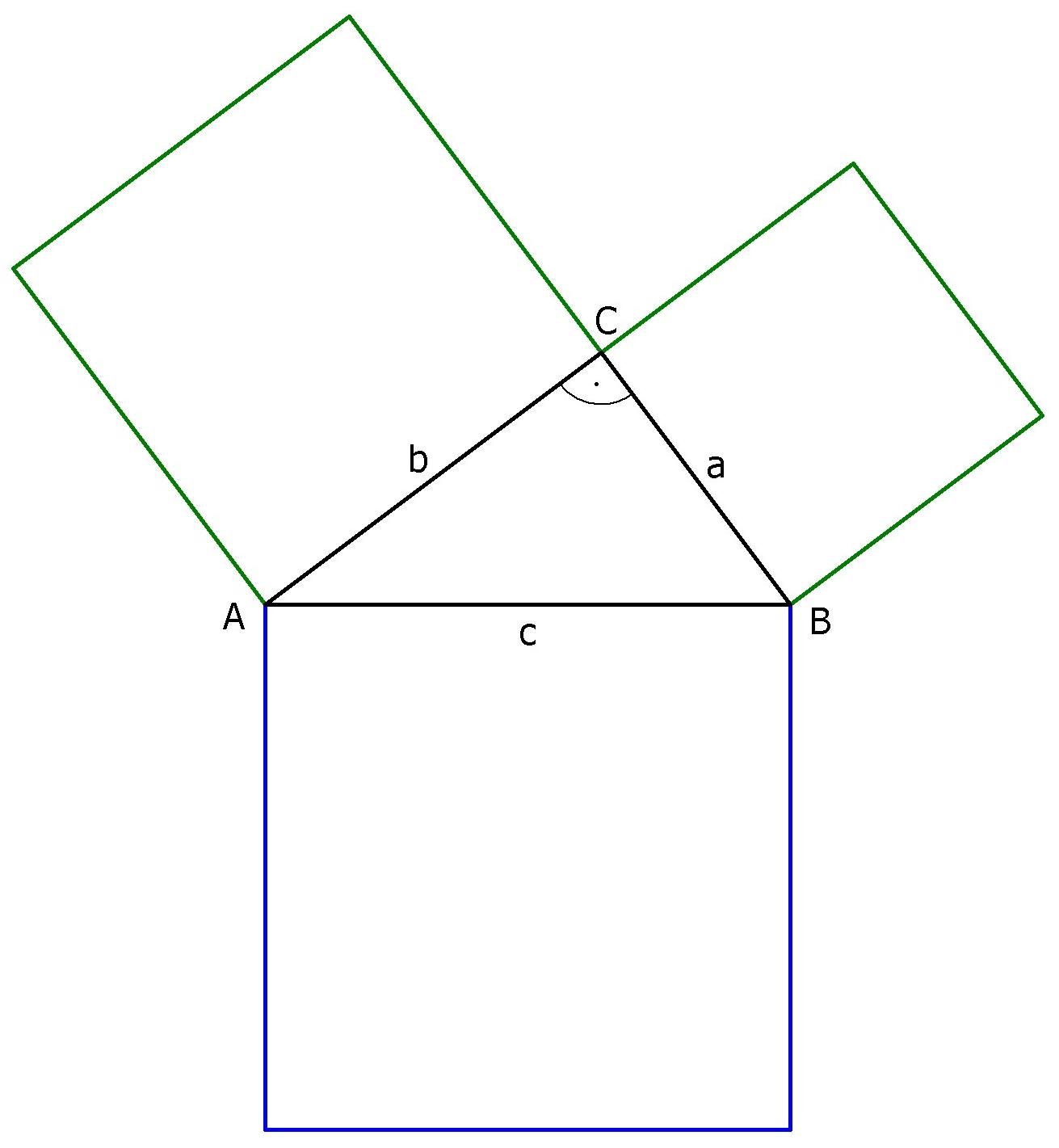
Als Satz formuliert: In ebenen rechtwinkligen Dreiecken entspricht die Summe der Flächeninhalte der Quadrate über den Katheten dem Flächeninhalt des Quadrats über der Hypotenuse. Der Satz des Pythagoras gilt natürlich auch in den beiden Teildreiecken, die sich in der Skizze ergeben, da die Höhe und die Hypotenuse einen rechten Winkel einschließen. Hierbei liegen die Seiten Es gilt also: |
 |
Der Höhensatz
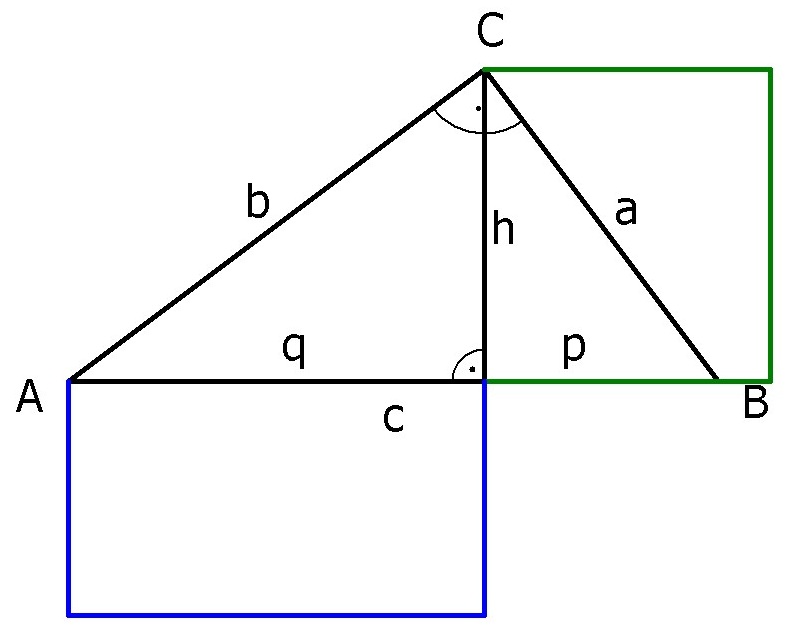
Als Satz formuliert: In ebenen rechtwinkligen Dreiecken entspricht der Flächeninhalt des Quadrats über der Höhe dem Flächeninhalt des Rechtecks, dessen Seiten die Hypotenusenabschnitte sind. |
 |
Die Kathetensätze
Ganz wichtig: Die Formel alleine ist nicht der Satz des Pythagoras! Durch die Formel ohne zusätzliche Informationen ist nämlich nicht festgelegt, welche Größen
,
und
bezeichnen (
und
müssen ja nicht automatisch die Katheten sein ...) bzw. ob es sich bei
,
und
überhaupt um Seiten eines rechtwinkligen Dreiecks handelt. Für irgendwelche beliebigen
,
und
wäre es denn auch eher überraschend, wenn sie die Beziehung
erfüllen würden. Warum sollten sie?
Genauso ist es natürlich auch beim Höhensatz und bei den Kathetensätzen.
Bemerkung: Bei konkreten Berechnungen müssen diese Formeln, die ja letztlich quadratische Gleichungen sind, teilweise umgeformt werden, z. B. um aus dem Höhensatz berechnen zu können.
Winkel im Grad- und Bogenmaß
Bislang haben wir uns nur um die Strecken in ebenen Figuren gekümmert. Winkel sind aber mindestens ebenso wichtig, wenn man sich mit geometrischen Objekten beschäftigt (spätenstens bei der Trigonometrie im nächsten Kapitel ...). Typischerweise werden Winkel mit griechischen Kleinbuchstaben bezeichnet, am liebsten mit (gesprochen: "alpha"),
(gesprochen: "beta"),
(gesprochen: "gamma"),
(gesprochen: "delta"),
(gesprochen: "epsilon") und
(gesprochen: "phi"). Grundsätzlich steht es einem aber frei, auch andere Bezeichnungen zu wählen - das kann allerdings zu Verwirrung führen.
Die Größe von Winkeln kann entweder im Gradmaß oder im Bogenmaß angegeben werden. Das ist ein bisschen so, wie die Länge von Strecken in Kilometern oder Meilen angegeben werden kann. Bei Winkeln wie bei Strecken haben wir also zwei gültige und sinnvolle Maße, und in beiden Fällen muss man wissen, wie man zwischen den Maßen hin- und herrechnet.
Das Gradmaß ist vermutlich den meisten ziemlich vertraut, schon deshalb, weil es eine entsprechende Skala auf jedem Geodreieck gibt. Daher nur kurz und knapp die wichtigsten Fakten:
- Wird ein Winkel im Gradmaß angegeben, wird dies durch die Einheit
gekennzeichnet.
- Ein Vollkreis hat
.
- Ein rechter Winkel hat
.
- Auf dem Taschenrechner wird das Gradmaß meist durch "D" oder "DEG" für "degree" (englisch für "Grad") gekennzeichnet.
Das Bogenmaß ist weniger verbreitet, hat aber in einigen Bereichen ziemliche Vorteile, dazu unten mehr.
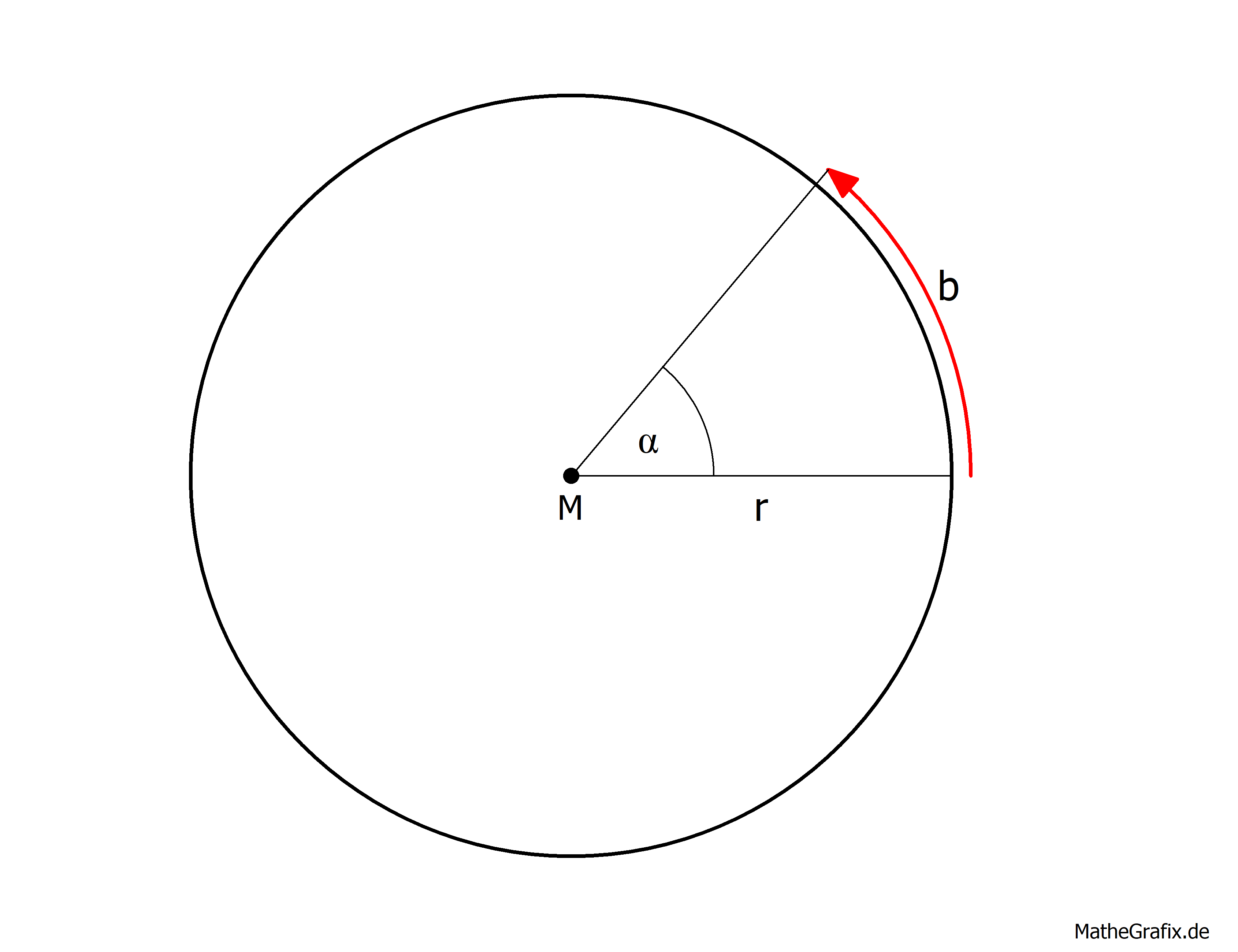
Definition: Das Bogenmaß eines Winkels am Mittelpunkt des Kreises ist das Verhältnis der Länge des Kreisbogens
zum Radius
:
 |
|
Beispiele für die Umrechnung:
Hier ein paar Fakten zum Bogenmaß:
- Winkelgrößen im Bogenmaß sind dimensionslos. Das heißt, sie haben keine Einheit. [Für diejenigen unter Ihnen, die Einheitenbetrachtungen gewöhnt sind: Bei der Berechnung des Bogenmaßes werden zwei Längen durcheinander geteilt: die Länge des Kreisbogens und die Länge des Radius. Da kürzen sich die Einheiten raus.]
- Ein rechter Winkel hat
.
- Meist wird das Bogenmaß als Vielfaches von
angegeben, z. B.
oder
, wodurch es einfach ist, die Winkelgröße z. B. mit einem Vollkreis (
) zu vergleichen.
- Auf dem Taschenrechner wird das Bogenmaß meist durch "R" oder "RAD" für "radiant" (hat mit dem Begriff "Radius" zu tun) gekennzeichnet.
Zu den Vorteilen vom Bogenmaß:
- Auch wenn es auf den ersten Blick vielleicht nicht so aussieht: Vieles wird übersichtlicher, wenn man das Bogenmaß verwendet.
Bei Winkelgrößen unterhaben die meisten genügend Erfahrung, um Größenordnungen abschätzen zu können, beispielsweise:
entspricht einem Dreiviertelkreis.
ist knapp ein rechter Winkel.
Bei Winkelgrößen überwird das schon schwieriger, z. B.
entspricht eineinhalb Kreisumläufen (
für einen Vollkreis und noch einen halben Kreis dazu). Wenn der Winkel mit
angegeben wäre, wäre das nicht so leicht zu erfassen.
- Je größer die Werte werden, desto deutlich wird das: Es ist nicht schwer herauszufinden, dass
dem Winkel für
Kreisumläufe entsprechen.
Kreisumläufe im Gradmaß sind
. Bei Zahlen in dieser Größenordnung erkennt man nicht mehr einfach so, ob dies eine ganze Kreisumdrehung beschreibt ...
- Verwendet man Winkel im Bogenmaß, verhalten sich trigonometrische Funktionen beim Ableiten angenehmer, da man sich nicht um eine Einheit kümmern muss.
- Auch wenn Sinus, Kosinus und Co. ursprünglich den mathematischen Zusammenhang von Seiten und Winkeln an konkreten Dreiecken beschreiben (siehe nächstes Kapitel), ist der Anwendungsbereich von trigonometrischen Funktionen sehr viel größer und auch abstrakter. Eine dimensionslose Variable ist dann deutlich naheliegender, da viele der Anwendungsfälle mit Winkeln rein gar nichts zu tun haben. Beispielsweise werden trigonometrische Funktionen auch benutzt, um die periodische Anteile in wirtschaftlichen Zeitreihendaten zu beschreiben.
- Wenn man Funktionen analysiert, gehört es quasi dazu, dass die Variable auch mal negative Werte annehmen kann. Das funktioniert besser, wenn man mit einer abstrakten Größe wie dem Bogenmaß rechnet und nicht an der Vorstellung eines Winkels hängt.
- In der Physik, wenn es um Kreisbewegungen geht, bietet sich das Bogenmaß geradezu an, weil man dort ja sowieso mit Kreisbögen und Radien zu tun hat.
Winkelsummen
Für Drei- und Vierecke gelten bestimmte Gesetzmäßigkeiten für die Summen der Winkel, die innerhalb der Figur liegen:
Winkelsummensatz für Dreiecke:
In jedem Dreieck beträgt die Summe der Innenwinkel bzw.
.
Winkelsummensatz für Vierecke:
In jedem Viereck beträgt die Summe der Innenwinkel bzw.
.
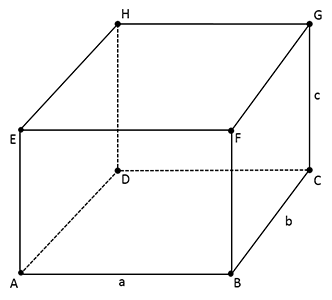
Dreidimensionale Körper
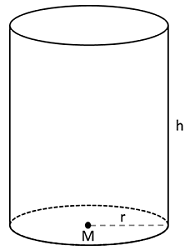
Definition: Die Mantelfläche ist die Oberfläche eines Körpers ohne die Grund- und (soweit vorhanden) Deckfläche.