Dieses Kapitel enthält die folgenden Themen:

• Bezeichnungen
• Rechnen mit rationalen Zahlen
• Quadratzahlen
• Teilbarkeitsregeln
• Runden

2.2 Grundlagen - Grundrechenarten

Wie der Name schon sagt, sind die Grundrechenarten die Grundlage aller weiteren Rechenoperationen. Daher lohnt es sich, einen Blick drauf zu werfen ... 

Bezeichnungen 

Die folgenden Bezeichnungen helfen, wenn über Rechnungen und Aufgaben gesprochen wird. Beispielsweise ist die Aussage "Einer der Summanden ist $3$." eindeutig und deutlich weniger umständlich als "Eine der Zahlen, die vor oder hinter dem Pluszeichen steht, ist $3$." Ebenso ist es bei "der Quotient aus $x$ und $y$" im Vergleich zu "das Ergebnis, das ich erhalte, wenn ich $x$ durch $y$ teile".
Die Bezeichnungen Minuend, Subtrahend, Dividend und Divisor werden weniger häufig verwendet. Man sollte aber zumindest wissen, zu welcher Rechenart sie gehören:

Dass man durch $0$ nicht teilen darf, ist hinlänglich bekannt. Warum ist das so? Die Division beantwortet die Frage "Wie oft muss man den Divisor vom Dividend abziehen, damit das Ergebnis $0$ ist?" Beispiel: $10 : 5$ Wir rechnen $10-5-5 = 0$. Die Antwort ist also $2$. Hätten wir $10 : 0$, kämen wir nie zu einer Antwort.
Ein praxisnäheres Beispiel: Wie verteilt man $10$ Objekte auf $5$ Plätze? Die Antwort: Auf jeden Platz kommen $2$ Objekte. Die Frage "Wie verteilt man $10$ Objekte auf $0$ Plätze?" lässt sich hingegen nicht sinnvoll beantworten.

Wichtig: Sobald Variablen ins Spiel kommen, sieht man manchmal nicht mehr so leicht, ob ein Divisor $0$ ist. Dann müssen spezielle Überlegungen angestellt werden, um diese Fälle auszuschließen.

Manchmal darf man auch ein bisschen faul sein bei der Notation: Solange Missverständnisse ausgeschlossen sind, darf der "Malpunkt" weggelassen werden:

• Beispielsweise meinen $a(b+c)$ und $a \cdot (b+c)$ dasselbe. Bei $5 \, t$ und $5 \cdot t$ ist das ebenso. Logischerweise muss bei Aufgaben wie $4 \cdot 7$ der "Malpunkt" immer hingeschrieben werden ...
• Auch kann der Faktor $1$ bei der Multiplikation weggelassen werden, z. B. ist $x = 1x = 1 \cdot x$.

Es ist in beiden Fällen natürlich nie falsch, den "Malpunkt" einfach mit hinzuschreiben.

Weitere Begriffe

Definition: Die Gegenzahl bzw. das Negative einer Zahl $a$ ist $-a$ . Es gilt: $a+(-a)=0$.
Bemerkung: $-a$ muss nicht kleiner $0$ sein. Im Gegenteil: Für alle negativen Zahlen ist die Gegenzahl positiv, z. B. ist $4$ die Gegenzahl zu $-4$.

Definition: Der Betrag einer Zahl $a$ , in einer Formel: $\left| a\right|$, ist ihr absoluter Wert. D. h. für positive Zahlen und $0$ entspricht der Betrag einer Zahl $a$ der Zahl selber, also $\left| a \right| = a$. Für negative Zahlen entspricht der Betrag einer Zahl $a$ ihrer Gegenzahl, also $\left| a \right| = -a$. Wichtig ist der Betrag z. B. bei Abstandsberechnungen, weil es dabei ja nur auf die absolute Entfernung ankommt und nicht auf die Richtung, in der diese Entfernung durchlaufen wird. Der Betrag, so wie er hier definiert ist, liefert für jede Zahl ihren Abstand vom Nullpunkt.

Definition: Der Kehrwert zu einer Zahl $a$ ist $\dfrac{1} {a}$. Man sagt auch $a$ und $\dfrac{1} {a}$ sind reziprok zueinander. Es gilt: $a \cdot \dfrac{1}{a}=1$.
Bemerkung 1: Da durch $0$ nicht geteilt werden darf, muss hierbei $a \neq 0$ gelten.
Bemerkung 2: $\frac {1}{a}$ muss nicht kleiner $1$ sein, z. B. ist $2$ der Kehrwert zu $\frac{1} {2}$.

Rechnen mit rationalen Zahlen

Es ist sehr wichtig, die folgenden Rechenregeln zu kennen, auch wenn in vielen Fällen natürlich der Taschenrechner weiterhilft. Sobald nämlich Variablen in den Rechnungen auftauchen, stoßen Taschenrechner sehr schnell an ihre Grenzen ...

Rechenregeln für die Addition rationaler Zahlen

Haben die beiden Summanden das gleiche Vorzeichen, werden die Beträge addiert. Die Summe bekommt das gemeinsame Vorzeichen.
Haben die beiden Summanden unterschiedliche Vorzeichen, zieht man den betragsmäßig kleineren Summanden vom betragsmäßig größeren ab. Die Summe bekommt das Vorzeichen des Summanden, der den größeren Betrag hat.

Die Subtraktion entspricht der Addition der Gegenzahl.

Das bedeutet konkret:

$\begin{array}{rcrcccc} 20+7 &=& 27 &=& +20+(+7) &=& +20-(-7) \cr \cr 20-7 &=& 13 &=& +20+(-7) &=& +20-(+7) \cr \cr -20+7 &=& -13 &=& -20+(+7) &=& -20-(-7) \cr \cr -20-7 &=& -27 &=& -20+(-7) &=& -20-(+7) \end{array}$

Rechenregeln für die Multiplikation rationaler Zahlen

Haben die beiden Faktoren das gleiche Vorzeichen, werden die Beträge multipliziert. Das Produkt ist positiv.
Haben die beiden Faktoren unterschiedliche Vorzeichen werden die Beträge multipliziert. Das Produkt ist negativ.

Kurze Merkregeln:

• "minus mal minus ist plus" bzw. "plus mal plus ist plus"
• "plus mal minus ist minus" bzw. "minus mal plus ist minus"

Die Division entspricht der Multiplikation mit dem Kehrwert.

Das bedeutet konkret:

$\begin{array}{rcccrcccl} 3 \cdot 9 &=& +3 \cdot (+9) &=& 27 &=& +3 : \left(+\frac{1}{9}\right) &=& 3 : \frac{1}{9} \cr \cr3 \cdot (-9) &=& +3 \cdot (-9) &=& -27 &=& +3 : \left(-\frac{1}{9}\right) &=& 3 : \left(-\frac{1}{9}\right) \cr \cr -3 \cdot 9 &=& -3 \cdot (+9) &=& -27 &=& -3 : \left(+\frac{1}{9}\right) &=& -3 : \frac{1}{9} \cr \cr & & -3 \cdot (-9) &=& 27 &=& -3 : \left(-\frac{1}{9}\right) \end{array}$

Bemerkung 1: "Überzählige" Pluszeichen (also Pluszeichen, die nur eine Vorzeichen- und keine Rechenfunktion haben) müssen nicht hingeschrieben werden.
Bemerkung 2: Immer, wenn ein Rechen- und ein Vorzeichen aufeinandertreffen, werden Klammern gesetzt.

Um die Regel “minus mal plus ist minus” ein bisschen plausibler zu machen, schauen wir uns Addition und Subtraktion auf dem Zahlenstrahl an:
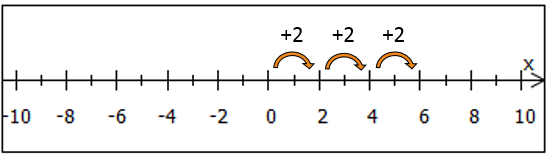
Addiert man eine positive Zahl, beispielsweise $2$, lässt sich dies auf dem Zahlenstrahl als $2$ Schritte nach rechts veranschaulichen. Addiert man die gleiche Zahl mehrfach, wiederholt man diese Schritte. Das kann man als Multiplikation auffassen. Beispiel: $2+2+2 = 6$ ergibt das Gleiche wie $3\cdot 2 = 6$.

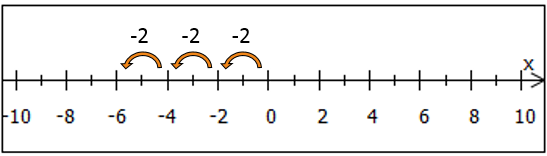
Subtrahiert man eine positive Zahl, beispielsweise $2$, lässt sich dies auf dem Zahlenstrahl als $2$ Schritte nach links veranschaulichen. Subtrahiert man die gleiche Zahl mehrfach, wiederholt man ebenfalls diese Schritte. Auch das kann man als Multiplikation auffassen. Beispiel: $-2-2-2 = -6$ ergibt das Gleiche wie $3\cdot (-2) = -6$. Man sieht also, dass die Multiplikation einer positiven mit einer negativen Zahl zu einem negativen Ergebnis führt.

Wichtig sind auch die Quadrat- und Kubikzahlen:

Bemerkung: In vielen Fällen wird ein Punkt gesetzt, um die einzelnen Tausender voneinander abzugrenzen. Manchmal wird stattdessen auch eine kleine Lücke in der Zahl gelassen. Verpflichtend ist beides nicht. Hauptsache, große Zahlen bleiben übersichtlich ...

Teilbarkeitsregeln

Vorab ein paar Begriffe:
Eine Zahl, die ohne Rest durch $2$ teilbar ist, nennt man gerade Zahl. Bleibt beim Teilen durch $2$ ein Rest, nennt man die Zahl ungerade.
Die Quersumme einer Zahl berechnet man, indem man einfach alle Ziffern addiert, z. B. ist die Quersumme von $123$: $1+2+3=6$

Die folgenden Regeln sind insofern bemerkenswert, weil sie Aussagen über die Teilbarkeit kompletter Zahlen ermöglichen - und dafür nur Teilinformationen heranziehen. Z. B. reicht es für die Aussage "$123.456$ ist durch $2$ teilbar." aus, die letzte Ziffer, nämlich die $6$, zu betrachten. Alle anderen Ziffern müssen gar nicht angeschaut werden. Sie sind nicht relevant. "Teilbar" meint hier immer "teilbar ohne Rest".
Diese Regeln werden sowohl bei der Bruchrechnung als auch bei Potenzen sehr weiterhelfen.

Eine Zahl, die nur durch $1$ und sich selbst teilbar ist, nennt man Primzahl. Jede Zahl ist durch $1$ und sich selbst teilbar - das Besondere an Primzahlen ist, dass sie keine weiteren Teiler haben.

Runden

Gerundet wird u. a., um die Anzahl der Nachkommastellen zu reduzieren oder wenn nur die Größenordnung einer Zahl, nicht aber der exakte Wert wichtig ist. Fürs Runden gibt es folgende Regeln:

• Abrunden: Ist die erste wegzulassende Dezimalstelle kleiner als $5$, wird abgerundet.
• Aufrunden: Ist die erste wegzulassende Dezimalstelle größer oder gleich $5$, wird aufgerundet.

Nach dem Runden ist es wichtig, das Ungefährzeichen $\approx$ anstelle des Gleichheitszeichens $=$ zu verwenden, weil durch das Runden ja Genauigkeit verloren geht.

Ein paar Beispiele:
Beim Runden auf eine Nachkommastelle ist die zweite Nachkommastelle ausschlaggebend. Alle anderen Stellen werden ignoriert.
$\begin{array}{rcl}1{,}44 &\approx& 1{,}4 \cr 2{,}48 &\approx& 2{,}5 \cr 5{,}12693 &\approx& 5{,}1 \end{array}$

Beim Runden auf drei Nachkommastellen ist die vierte Nachkommastelle ausschlaggebend. Alle anderen Stellen werden ignoriert.
$\begin{array}{ccrcl} & & 10{,}12348 &\approx& 10{,}123 \cr & & 8{,}8767 &\approx& 8{,}877 \cr 129{,} \overline3 &=& 129{,}3333 \ldots &\approx& 129{,}333 \end{array}$

Es kann auch auf ganze $100.000$ gerundet werden. Dann ist die $10.000$er Stelle ausschlaggebend. Alle anderen Stellen werden ignoriert.
$\begin{array}{rcl}872.146 &\approx& 900.000 \cr 927.549 &\approx& 900.000 \cr 590.190{,}12 &\approx& 600.000 \end{array}$

Natürlich könnte man auch auf andere Stellen runden.

Wichtig: Runden Sie bei komplexeren Aufgaben nicht zu früh, sondern rechnen Sie so lange wie möglich mit den exakten Werten, weil sich sonst die Rundungsfehler sehr schnell zu problematischen Größenordnungen anhäufen. Ein (zugegebenermaßen leicht übertriebenes) Beispiel:
$1.200\cdot 0{,}003 = 3{,}6$
Rundet man die $0{,}003$ korrekt auf zwei Stellen nach dem Komma, erhält man $0$. Aus unserer Rechnung würde dann $1.200\cdot 0 = 0$
Dass dies kein geschicktes Vorgehen ist, wird spätestens dann deutlich, wenn man sich überlegt, was in dieser Rechnung mit anderen Faktoren passieren würde: Es ist nun völlig egal, ob man $1.200$ mit der "gerundeten $0{,}003$" multipliziert oder $-10.819$ oder $6{,}841841$ - das Ergebnis ist immer $0$.