Übersicht:

• Lösung zur 1. Aufgabe
• Lösung zur 2. Aufgabe
• Lösung zur 3. Aufgabe
• Lösung zur 4. Aufgabe
• Lösung zur 5. Aufgabe
• Lösung zur 6. Aufgabe
• Lösung zur 7. Aufgabe
• Lösung zur 8. Aufgabe
• Lösung zur 9. Aufgabe
• Lösung zur 10. Aufgabe

10.3 Quadratische Funktionen - Lösungen

1. Aufgabe

Der Übersichtlichkeit wegen sind die Graphen von Aufgabe 1a) in zwei Koordinatensysteme aufgeteilt. Bitte achten Sie bei den Grafiken auf die unterschiedliche Skalierung der Achsen!

a)

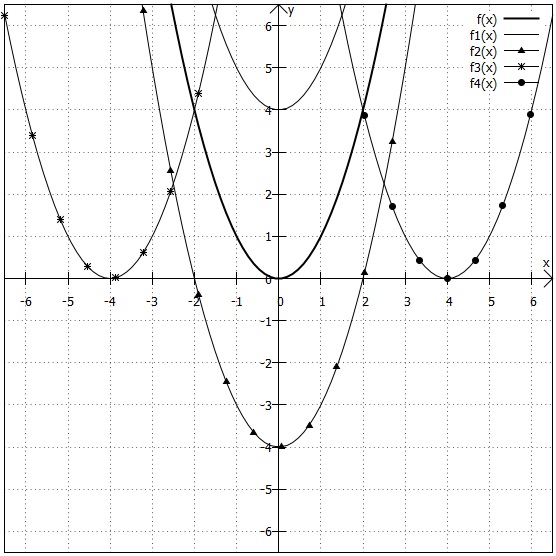
b)

1)
Der Graph von $f_1(x)$ ist nach oben geöffnet und gestaucht, da der Koeffizient von $x^2$ ein positiver, echter Bruch ist. Zusätzlich wird von den Funktionswerten jeweils $12$ subtrahiert, sodass der Scheitelpunkt bei $S(0 \mid -12)$ liegt.

2)
Der Graph von $f_2(x)$ ist nach unten geöffnet und gestreckt, da der Koeffizient von $x^2$ kleiner als $-1$ ist. Die Funktionsgleichung liegt in Scheitelpunktform vor, sodass man den Scheitelpunkt ablesen kann: $S(3 \mid 0)$.

3)
Der Graph von $f_3(x)$ ist nach oben geöffnet und weder gestreckt noch gestaucht (Normalparabel), da der Koeffizient von $x^2$ exakt $1$ ist. Die Funktionsgleichung liegt in Scheitelpunktform vor, sodass man den Scheitelpunkt ablesen kann: $S(5 \mid 5)$.

4)
Der Graph von $f_4(x)$ ist nach oben geöffnet und gestreckt, da der Koeffizient von $x^2$ ein positiver, unechter Bruch ist. Die Funktionsgleichung liegt in Scheitelpunktform vor, sodass man den Scheitelpunkt ablesen kann: $S\left(-10 \mid 2\right)$.

5)
Der Graph von $f_5(x)$ ist nach oben geöffnet und weder gestreckt noch gestaucht (Normalparabel), da der Koeffizient von $x^2$ exakt $1$ ist. Die Funktionsgleichung liegt in Scheitelpunktform vor, sodass man den Scheitelpunkt ablesen kann: $S\left(-\dfrac{1}{2} \mid -4\right)$.

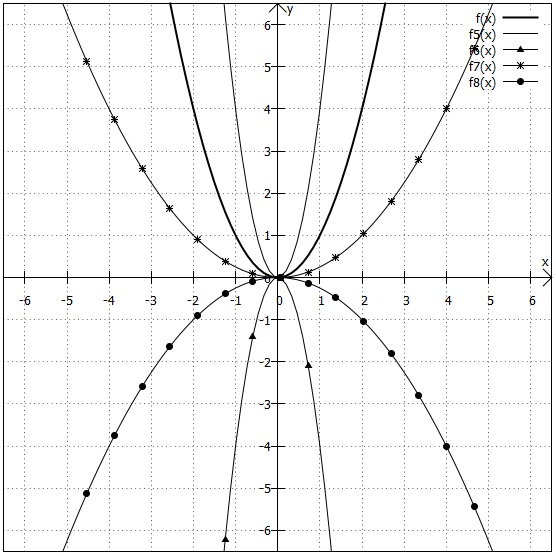
6)
Der Graph von $f_6(x)$ ist nach oben geöffnet und weder gestreckt noch gestaucht (Normalparabel), da der Koeffizient von $x^2$ exakt $1$ ist. Zusätzlich wird von den Funktionswerten jeweils $8$ subtrahiert, sodass der Scheitelpunkt bei $S(0 \mid -8)$ liegt.

7)
Der Graph von $f_7(x)$ ist nach unten geöffnet und gestaucht, da der Koeffizient von $x^2$ ein negativer, echter Bruch ist. Die Funktionsgleichung liegt in Scheitelpunktform vor, sodass man den Scheitelpunkt ablesen kann: $S\left(9 \mid 0\right)$.

8)
Der Graph von $f_8(x)$ ist nach unten geöffnet und weder gestreckt noch gestaucht (Normalparabel), da der Koeffizient von $x^2$ exakt $-1$ ist. Die Funktionsgleichung liegt in Scheitelpunktform vor, sodass man den Scheitelpunkt ablesen kann: $S\left(-6 \mid 4\right)$.

9)
Der Graph von $f_9(x)$ ist nach unten geöffnet und weder gestreckt noch gestaucht (Normalparabel), da der Koeffizient von $x^2$ exakt $-1$ ist. Zusätzlich wird zu den Funktionswerten jeweils $2$ addiert, sodass der Scheitelpunkt bei $S(0 \mid 2)$ liegt.

10)
Der Graph von $f_{10}(x)$ ist nach oben geöffnet und weder gestreckt noch gestaucht (Normalparabel), da der Koeffizient von $x^2$ exakt $1$ ist. Die Funktionsgleichung liegt in Scheitelpunktform vor, sodass man den Scheitelpunkt ablesen kann: $S\left(3{,}5 \mid 0\right)$.

2. Aufgabe

Vorüberlegungen zur Lösung:
Um zu erkennen, wie viele Nullstellen eine Funktion hat, setzen wir den Funktionsterm null und schauen uns die entstehende quadratische Gleichung an. Wichtig: Wir müssen die Gleichung (diesmal) nicht lösen, da ja nur gefragt ist, wie viele Nullstellen die Funktion hat und nicht, wo sie liegen. Dazu folgende Überlegungen:

• Liegt die quadratische Gleichung in faktorisierter Form vor oder kann leicht in diese Form gebracht werden, liefert jeder Faktor eine Lösung. Die Funktion hat also zwei Nullstellen.
• Bei quadratischen Gleichungen, die durch Umformen gelöst werden können, gibt es zwei Möglichkeiten (Beispielrechnungen siehe hier: 1. Fall und 3. Fall):
  
  • Haben der quadratische und der absolute Term verschiedene Vorzeichen, hat die Gleichung zwei Lösungen und die Funktion somit zwei Nullstellen.
  • Hat der quadratische Term das gleiche Vorzeichen wie der absolute, ist die Gleichung im Bereich der reellen Zahlen nicht lösbar. Die Funktion hat somit keine Nullstellen.
• Ist in der Gleichung nur ein quadratischer Term enthalten, gibt es eine Nullstelle. 
• Auch wenn der Funktionsterm in Form einer binomischen Formel vorliegt, hat die Funktion eine Nullstelle (Beispielrechnung siehe hier: 2. Fall).
• Liegen Funktionsterme in Normal- oder allgemeiner Form vor, kommen wir mit diesen Überlegungen nicht weiter. Dann müssten wir doch rechnen ...

Parabeln dieser Art sind alle achsensymmetrisch (Genauer schauen wir uns dieses Thema im nächsten Kapitel an ...). Die Frage, die sich hier dahinter verbirgt, ist eigentlich "nur", ob die Parabel in x-Richtung verschoben ist.
Ist sie nicht in x-Richtung verschoben, liegt also ihr Scheitelpunkt bei $x=0$, ist die Parabel symmetrisch zur y-Achse. 
In allen anderen Fällen (egal, in welche Richtung und wie viel sie verschoben ist) ist die Parabel symmetrisch zu einer Parallelen der y-Achse. Das ist auch dann der Fall, wenn der Funktionsterm faktorisiert vorliegt und durch Ausmultiplizieren in allgemeine Form gebracht werden kann. Nur wenn die Nullstellen symmetrisch zur y-Achse liegen, also z. B. bei $f(x)=(x-4)(x+4)$, ergibt sich keine Verschiebung in x-Richtung.

Nun die Lösungen der einzelnen Aufgaben:

1)
Da die entstandene Gleichung durch Umformen gelöst werden kann und die beiden Terme unterschiedliche Vorzeichen haben, hat die Funktion zwei Nullstellen.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm in der Form $f(x)=x^2+e$ vorliegt, ist der Graph nur nach oben verschoben. Damit ist er achsensymmetrisch zur y-Achse.
Da der Koeffizient von $x^2$ einen Betrag von $1$ hat, ist diese Parabel genauso steil wie eine Normalparabel.

2)
Da die entstandene Gleichung in allgemeiner Form vorliegt, kann die Anzahl der Nullstellen ohne Rechnung nicht bestimmt werden.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet.
Da der Funktionsterm in allgemeiner Form vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag größer als $1$ hat, ist diese Parabel steiler als eine Normalparabel.

3)
Da die entstandene Gleichung durch Ausklammern faktorisiert werden kann, hat die Funktion zwei Nullstellen.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm in allgemeiner Form vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag größer als $1$ hat, ist diese Parabel steiler als eine Normalparabel.

4)
Da die entstandene Gleichung faktorisiert vorliegt, hat die Funktion zwei Nullstellen.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet.
Da der Funktionsterm durch Ausmultiplizieren in allgemeine Form gebracht werden kann, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag größer als $1$ hat, ist diese Parabel steiler als eine Normalparabel.

5)
Da die entstandene Gleichung nur einen quadratischen Term enthält, hat die Funktion eine Nullstelle.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm in der Form $f(x)=ax^2$ vorliegt, ist der Graph nur gestreckt/gestaucht. Damit ist er achsensymmetrisch zur y-Achse.
Da der Koeffizient von $x^2$ einen Betrag kleiner als $1$ hat, ist diese Parabel weniger steiler als eine Normalparabel.

6)
Da die entstandene Gleichung in allgemeiner Form vorliegt, kann die Anzahl der Nullstellen ohne Rechnung nicht bestimmt werden.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm in allgemeiner Form vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag kleiner als $1$ hat, ist diese Parabel weniger steiler als eine Normalparabel.

7)
Da die entstandene Gleichung durch Umformen gelöst werden kann und die beiden Terme das gleiche Vorzeichen haben, hat die Funktion keine Nullstellen.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet.
Da der Funktionsterm in der Form $f(x)=ax^2+e$ vorliegt, ist der Graph nur gestreckt/gestaucht und nach oben verschoben. Damit ist er achsensymmetrisch zur y-Achse.
Da der Koeffizient von $x^2$ einen Betrag kleiner als $1$ hat, ist diese Parabel weniger steiler als eine Normalparabel.

8)
Da die entstandene Gleichung in Normalform vorliegt, kann die Anzahl der Nullstellen ohne Rechnung nicht bestimmt werden.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet.
Da der Funktionsterm in Normalform vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag von $1$ hat, ist diese Parabel genauso steil wie eine Normalparabel.

9)
Da die entstandene Gleichung durch Ausklammern faktorisiert werden kann, hat die Funktion zwei Nullstellen.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet.
Da der Funktionsterm in allgemeiner Form vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag kleiner als $1$ hat, ist diese Parabel weniger steiler als eine Normalparabel.

10)
Da die entstandene Gleichung in allgemeiner Form vorliegt, kann die Anzahl der Nullstellen ohne Rechnung nicht bestimmt werden.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm in allgemeiner Form vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag von $1$ hat, ist diese Parabel genauso steil wie eine Normalparabel.

11)
Da die entstandene Gleichung durch Umformen gelöst werden kann und die beiden Terme das gleiche Vorzeichen haben, hat die Funktion keine Nullstellen.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm in der Form $f(x)=ax^2-e$ vorliegt, ist der Graph nur gestreckt/gestaucht und nach unten verschoben. Damit ist er achsensymmetrisch zur y-Achse.
Da der Koeffizient von $x^2$ einen Betrag kleiner als $1$ hat, ist diese Parabel weniger steiler als eine Normalparabel.

12)
Da die entstandene Gleichung in Form einer binomischen Formel vorliegt, hat die Funktion eine Nullstelle.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet.
Da der Funktionsterm durch Ausmultiplizieren in allgemeine Form gebracht werden kann, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag von $1$ hat, ist diese Parabel genauso steil wie eine Normalparabel.

13)
Da die entstandene Gleichung faktorisiert vorliegt, hat die Funktion zwei Nullstellen.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet.
Da der Funktionsterm durch Ausmultiplizieren in allgemeine Form gebracht werden kann, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag größer als $1$ hat, ist diese Parabel steiler als eine Normalparabel.

14)
Da die entstandene Gleichung in Form einer binomischen Formel vorliegt, hat die Funktion eine Nullstelle.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet.
Da der Funktionsterm durch Ausmultiplizieren in allgemeine Form gebracht werden kann, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag kleiner als $1$ hat, ist diese Parabel weniger steiler als eine Normalparabel.

15)
Da die entstandene Gleichung in allgemeiner Form vorliegt, kann die Anzahl der Nullstellen ohne Rechnung nicht bestimmt werden.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm in allgemeiner Form vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag kleiner als $1$ hat, ist diese Parabel weniger steiler als eine Normalparabel.

16)
Da die entstandene Gleichung in allgemeiner Form vorliegt, kann die Anzahl der Nullstellen ohne Rechnung nicht bestimmt werden.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet. Da der Funktionsterm in allgemeiner Form vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag größer als $1$ hat, ist diese Parabel steiler als eine Normalparabel.

17)
Da die entstandene Gleichung in allgemeiner Form vorliegt, kann die Anzahl der Nullstellen ohne Rechnung nicht bestimmt werden.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm in allgemeiner Form vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag größer als $1$ hat, ist diese Parabel steiler als eine Normalparabel.

18)
Da die entstandene Gleichung in Form einer binomischen Formel vorliegt, hat die Funktion eine Nullstelle.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm durch Ausmultiplizieren in allgemeine Form gebracht werden kann, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag größer als $1$ hat, ist diese Parabel steiler als eine Normalparabel.

19)
Da die entstandene Gleichung in Normalform vorliegt, kann die Anzahl der Nullstellen ohne Rechnung nicht bestimmt werden.
Da der Koeffizient von $x^2$ größer als $0$ ist, ist diese Parabel nach oben geöffnet.
Da der Funktionsterm in allgemeiner Form vorliegt, ist der Graph auch in x-Richtung verschoben. Damit ist er achsensymmetrisch zu einer Parallelen der y-Achse.
Da der Koeffizient von $x^2$ einen Betrag von $1$ hat, ist diese Parabel genauso steil wie eine Normalparabel.

20)
Da die entstandene Gleichung durch Umformen gelöst werden kann und die beiden Terme das gleiche Vorzeichen haben, hat die Funktion keine Nullstellen.
Da der Koeffizient von $x^2$ kleiner als $0$ ist, ist diese Parabel nach unten geöffnet.
Da der Funktionsterm in der Form $f(x)=ax^2-e$ vorliegt, ist der Graph nur gestreckt/gestaucht und nach unten verschoben. Damit ist er achsensymmetrisch zur y-Achse.
Da der Koeffizient von $x^2$ einen Betrag größer als $1$ hat, ist diese Parabel steiler als eine Normalparabel.

3. Aufgabe

Vorgehen:

1. Ablesen der Koordinaten des Scheitelpunkts aus der Grafik und einsetzen der Koordinaten in die Scheitelpunktform der Parabel $f(x)=a(x-d)^2+e$, um $d$ und $e$ zu bestimmen
2. Feststellen, ob die Parabel nach oben oder nach unten geöffnet ist, um zu bestimmen, ob $a$ positiv oder negativ ist
3. Ermitteln des Streckungs-/Stauchungsfaktors $a$
4. Wenn man möchte: Ausmultiplizieren des Terms

Zur Vorbereitung ist es hilfreich, Aufgabe 1 und Aufgabe 6 bei den linearen Funktionen bearbeitet zu haben.

$f_1(x) = 2x^2$
Begründung:
Die Funktion hat ihren Scheitel im Punkt $\left(0\mid 0\right)$, ist also weder nach links/rechts noch nach oben/unten verschoben.
Sie ist um den Faktor $2$ gestreckt, weil sie nicht (wie eine Normalparabel) durch den Punkt $\left(1\mid 1\right)$ , sondern durch den Punkt $\left(2\mid 1\right)$ verläuft.

$f_2(x) = (x-4)^2$
Begründung:
Die Funktion hat ihren Scheitel im Punkt $\left(4\mid 0\right)$ , ist also um $4$ Einheiten nach rechts, aber nicht nach oben/unten verschoben.
Es handelt sich um eine Normalparabel, weil sie durch den Punkt $\left(5\mid 1\right)$ verläuft.

$f_3(x) = x^2+\dfrac{3}{2}$
Begründung:
Die Funktion hat ihren Scheitel im Punkt $\left(0\mid \frac{3}{2}\right)$, ist also nicht nach links/rechts, aber um $1{,}5$ Einheiten nach oben verschoben.
Es handelt sich um eine Normalparabel, weil sie durch den Punkt $\left(1\mid \frac{5}{2}\right)$ verläuft.

$f_4(x) = (x+1)^2-3$
Begründung:
Die Funktion hat ihren Scheitel im Punkt $\left(-1\mid -3\right)$, ist also um $1$ Einheit nach links und um $3$ Einheiten nach unten verschoben.
Es handelt sich um eine Normalparabel, weil sie durch den Punkt $\left(0\mid -2\right)$ verläuft.

$f_5(x) = -\dfrac{1}{4}(x-2)^2+1$
Begründung:
Die Funktion hat ihren Scheitel im Punkt $\left(2 \mid 1\right)$, ist also um $2$ Einheiten nach rechts und um $1$ Einheit nach oben verschoben.
Sie ist um den Faktor $\frac{1} {4}$ gestaucht, weil sie nicht (wie eine Normalparabel) durch den Punkt $\left(4\mid -3\right)$, sondern durch den Punkt $\left(4\mid 0\right)$ verläuft.
Das Minuszeichen nicht vergessen; schließlich ist die Parabel nach unten geöffnet.

4. Aufgabe

1)
a)
$\begin{array}{rclll} f(7) &=& 7 \cdot 7^2-14 \cdot 7+49 &=& 294 \quad \rightarrow \quad P_1(7 \mid 294) \end{array}$

b)
$\begin{array}{rclcll} 105 &=& 7x^2-14x+49 & \vert & -105 \cr 0 &=& 7x^2-14x-56 & \vert & :7 \cr 0 &=& x^2-2x-8 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& 1 \pm \sqrt{(-1)^2+8} \cr x_{1,2} &=& 1 \pm \sqrt{9} \cr\cr x_1 &=& 1+3 = 4 & \rightarrow \quad P_2(4 \mid 105) \cr x_2 &=& 1-3 = -2 & \rightarrow \quad P_3(-2 \mid 105) \end{array}$

2)
a)
$\begin{array}{rclll} f(-11{,}5) &=& -(-11{,}5)^2-24 \cdot (-11{,}5)+2 &=& 145{,}75 \quad \rightarrow \quad P_1(-11{,}5 \mid 145{,}75) \end{array}$

b)
$\begin{array}{rclcll} 25 &=& -x^2-24x+2 &\vert & -25 \cr 0 &=& -x^2-24x-23 &\vert & \cdot(-1) \cr 0 &=& x^2+24x+23 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& -12 \pm \sqrt{12^2-23} \cr x_{1,2} &=& -12 \pm \sqrt{121} \cr\cr x_1 &=& -12+11 = -1 & \rightarrow \quad P_2(-1 \mid 25) \cr x_2 &=& -12-11 = - 23 & \rightarrow \quad P_3(-23 \mid 25) \end{array}$

3)
a)
$\begin{array}{rclll} f(8) &=& 32 \cdot 8^2-8 &=& 2040 \quad \rightarrow \quad P_1(8 \mid 2.040) \end{array}$

b)
$\begin{array}{rclcl} -4 &=& 32x^2-x &\vert & +4 \cr 0 &=& 32x^2-x+4 &\vert & :32 \cr 0 &=& x^2-\dfrac{1}{32}x+\dfrac{1}{8} &\vert& \text{p-q-Formel} \cr x_{1,2} &=& \dfrac{1}{64} \pm \sqrt{\left(-\dfrac{1}{64}\right)^2-\dfrac{1}{8}} \cr x_{1,2} &=& \dfrac{1}{64} \pm \sqrt{-\dfrac{511}{4.096}}\end{array}$

Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Gleichung keine Lösung: Das bedeutet, dass die Funktion nirgends den Funktionswert $-4$ annimmt.

4)
a)
$\begin{array}{rclll} f(6) &=& -3 \cdot 6^2+7 \cdot 6 &=& -66 \quad \rightarrow \quad P_1(6 \mid -66) \end{array}$

b)
$\begin{array}{rclcll} 4 &=& -3x^2+7x &\vert & -4 \cr 0 &=& -3x^2+7x-4 &\vert & :(-3) \cr 0 &=& x^2-\dfrac{7}{3}x+\dfrac{4}{3} &\vert& \text{p-q-Formel} \cr x_{1,2} &=& \dfrac{7}{6} \pm \sqrt{\left(-\dfrac{7}{6}\right)^2-\dfrac{4}{3}} \cr x_{1,2} &=& \dfrac{7}{6} \pm \sqrt{\dfrac{1}{36}} \cr\cr x_1 &=& \dfrac{7}{6}+\dfrac{1}{6} = \dfrac{4}{3} & \rightarrow \quad P_2\left(\dfrac{4}{3} \mid 4\right) \cr x_2 &=& \dfrac{7}{6}-\dfrac{1}{6} = 1 & \rightarrow \quad P_3(1 \mid 4) \end{array}$

5)
a)
$\begin{array}{rclll} g\left(-\dfrac{5}{6}\right) &=& 6 \cdot \left(-\dfrac{5}{6}\right)^2-17 &=& -\dfrac{77}{6} \quad \rightarrow \quad P_1\left(-\dfrac{5}{6} \mid -\dfrac{77}{6}\right) \end{array}$

b)
$\begin{array}{rclcl} 0 &=& 6x^2-17 &\vert & :6 \cr 0 &=& x^2-\dfrac{17}{6} &\vert & -x^2 \cr -x^2 &=& -\dfrac{17}{6} &\vert & :(-1) \cr x^2 &=& \dfrac{17}{6} &\vert & \pm\sqrt{} \cr\cr x_1 &=& -\sqrt{\dfrac{17}{6}} & \rightarrow \quad P_2\left(-\sqrt{\dfrac{17}{6}} \mid 0\right) \cr x_2 &=& \sqrt{\dfrac{17}{6}} & \rightarrow \quad P_3\left(\sqrt{\dfrac{17}{6}} \mid 0\right) \end{array}$

6)
a)
$\begin{array}{rclll} f(17) &=& 2(17-1)^2-\dfrac{4}{3} &=& \dfrac{1.532}{3} \quad \rightarrow \quad P_1\left(17 \mid \dfrac{1.532}{3}\right) \end{array}$

b)
$\begin{array}{rclcll} -\dfrac{4}{3} &=& 2(x-1)^2-\dfrac{4}{3} &\vert & +\dfrac{4}{3} \cr 0 &=& 2(x-1)^2 &\vert & :2 \cr 0 &=& (x-1)^2 &\vert & \sqrt{} \cr 0 &=& x-1 &\vert& +1 \cr 1 &=& x & & \rightarrow \quad P_2\left(1 \mid -\dfrac{4}{3}\right) \end{array}$

7)
a)
$\begin{array}{rclll} f\left(\dfrac{15}{4}\right) &=& \left(-3+\dfrac{15}{4}\right)^2-6 &=& -\dfrac{87}{16} \quad \rightarrow \quad P_1\left(\dfrac{15}{4} \mid -\dfrac{87}{16}\right) \end{array}$

b)
$\begin{array}{rclcl} -43 &=& (-3+a)^2-6 &\vert & +43 \cr 0 &=& (3-a)^2+37 \cr 0 &=& a^2-6a+46 &\vert& \text{p-q-Formel} \cr a_{1,2} &=& 3 \pm \sqrt{(-3)^2-46} \cr a_{1,2} &=& 3 \pm \sqrt{-37}\end{array}$

Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Gleichung keine Lösung: Das bedeutet, dass die Funktion nirgends den Funktionswert $-43$ annimmt.

8)
a)
$\begin{array}{rclll} f(5) &=& (4\cdot 5+12)^2+8 &=& 1.032 \quad \rightarrow \quad P_1(5 \mid 1.032) \end{array}$

b)
$\begin{array}{rclll} 8 &=& (4x+12)^2+8 &\vert & -8 \cr 0 &=& (4x+12)^2 &\vert & \sqrt{} \cr 0 &=& 4x+12 &\vert & -4x \cr -4x &=& 12 &\vert & :(-4) \cr x &=& -3 & & \rightarrow \quad P_2(-3 \mid 8) \end{array}$

9)
a)
$\begin{array}{rclll} f(18) &=& \dfrac{1}{10}(18-7)^2 &=& \dfrac{121}{10} \quad \rightarrow \quad P_1\left(18 \mid \dfrac{121}{10}\right) \end{array}$

b)
$\begin{array}{rclll} 0 &=& \dfrac{1}{10}(x-7)^2 &\vert & \cdot 10 \cr 0 &=& (x-7)^2 &\vert& \sqrt{} \cr 0 &=& x-7 &\vert & +7 \cr 7 &=& x & & \rightarrow \quad P_2(7 \mid 0) \end{array}$

10)
a)
$\begin{array}{rclll} f(0{,}5) &=& 100 \cdot 0{,}5^2-50 \cdot 0{,}5+25 &=& 25 \quad \rightarrow \quad P_1(0{,}5 \mid 25) \end{array}$

b)
$\begin{array}{rclcll} 775 &=& 100x^2-50x+25 &\vert & -775 \cr 0 &=& 100x^2-50x-750 &\vert & :100 \cr 0 &=& x^2-\dfrac{1}{2}x-\dfrac{15}{2} &\vert& \text{p-q-Formel} \cr x_{1,2} &=& \dfrac{1}{4} \pm \sqrt{\left(-\dfrac{1}{4}\right)^2+\dfrac{15}{2}} \cr x_{1,2} &=& \dfrac{1}{4} \pm \sqrt{\dfrac{121}{16}} \cr\cr x_1 &=& \dfrac{1}{4}+\dfrac{11}{4} = 3 & \rightarrow \quad P_2(3 \mid 775) \cr x_2 &=& \dfrac{1}{4}-\dfrac{11}{4} = -\dfrac{5}{2} & \rightarrow \quad P_3\left(-\dfrac{5}{2} \mid 775\right) \end{array}$

5. Aufgabe

1)
$\begin{array}{rcl} f(x) &=& x^2-6x+16 \cr &=& x^2-6x+9+7 \cr &=& x^2-2 \cdot 3x+3^2+7 \cr &=& (x-3)^2+7 \end{array}$

Der Scheitelpunkt liegt bei $S(3\mid 7)$.

2)
$\begin{array}{rcl} f(x) &=& 2x^2-4x+2 \cr &=& 2(x^2-2x+1) \cr &=& 2(x^2-2 \cdot 1x+1^2) \cr &=& 2(x-1)^2 \end{array}$

Der Scheitelpunkt liegt bei $S(1\mid 0)$.

3)
$\begin{array}{rcl} f(x) &=& -13x^2-8 \cr &=& -13(x-0)^2-8 \end{array}$

Der Scheitelpunkt liegt bei $S(0 \mid -8)$. Die Parabel ist nach unten geöffnet.

4)
$\begin{array}{rcl} f(x) &=& \dfrac{1}{4}x^2-6x+32 \cr \cr &=& \dfrac{1}{4}(x^2-24x+128) \cr \cr &=& \dfrac{1}{4}(x^2-24x+144-16) \cr \cr &=& \dfrac{1}{4}(x^2-2 \cdot 12x+12^2-16) \cr \cr &=& \dfrac{1}{4}((x-12)^2 -16) \cr \cr &=& \dfrac{1}{4}(x-12)^2-4 \end{array}$

Der Scheitelpunkt liegt bei $S(12 \mid -4)$.

5)
$\begin{array}{rcl} f(x) &=& -11x^2-44x-34 \cr &=& -11 \left(x^2+4x+\dfrac{34}{11} \right) \cr &=& -11 \left(x^2+2 \cdot 2x +4- \dfrac{10}{11} \right) \cr &=& -11 \left(x^2+2 \cdot 2x +2^2- \dfrac{10}{11} \right) \cr &=& -11 \left((x+2)^2- \dfrac{10}{11} \right) \cr &=& -11(x+2)^2+10 \end{array}$

Der Scheitelpunkt liegt bei $S(-2 \mid 10)$.

6)
$\begin{array}{rcl} f(x) &=& -9x^2 -90x -225 \cr &=& -9(x^2+10x+25) \cr &=& -9(x^2+2 \cdot 5x+ 5^2) \cr &=& -9(x+5)^2 \end{array}$

Der Scheitelpunkt liegt bei $S(-5 \mid 0)$.

7)
$\begin{array}{rcl} f(x) &=& 4x^2 -4x+3 \cr\cr &=& 4 \left(x^2- 1x+ \dfrac{3}{4} \right) \cr\cr &=& 4 \left(x^2 -1x+ \dfrac14 +\dfrac12 \right) \cr\cr &=& 4 \left(x^2 - 2 \cdot \dfrac12 x + \left(\dfrac12 \right)^2 + \dfrac12 \right) \cr\cr &=& 4 \left(\left(x- \dfrac12 \right)^2 +\dfrac{1}{2}\right) \cr\cr &=& 4 \left(x- \dfrac12 \right)^2 +2 \end{array}$

Der Scheitelpunkt liegt bei $S \left(\dfrac12 \mid 2 \right)$.

8)
$\begin{array}{rcl} f(x) &=& 3x^2 -4x - \dfrac{14}{3} \cr\cr &=& 3 \left(x^2 - \dfrac{4}{3} x- \dfrac{14}{9} \right) \cr\cr &=& 3 \left(x^2 - 2 \cdot \dfrac{2}{3}x + \left(\dfrac{2}{3} \right)^2 - \left(\dfrac{2}{3} \right)^2 - \dfrac{14}{9} \right) \cr\cr &=& 3 \left(x^2-2\cdot \dfrac{2}{3}x+ \left(\dfrac{2}{3} \right)^2 -2 \right) \cr\cr &=& 3 \left(x-\dfrac{2}{3} \right)^2 -6 \cr\cr &=& 3 \left(\left(x-\dfrac{2}{3} \right)^2 -2\right) \end{array}$

Der Scheitelpunkt liegt bei $S \left(\dfrac{2}{3} \mid -6 \right)$.

9)
$\begin{array}{rcl} f(x) &=& \dfrac12 x^2 +4x-7 \cr\cr &=& \dfrac12 \left(x^2 +8x-14 \right) \cr\cr &=& \dfrac12 (x^2 +2 \cdot 4x +4^2 -4^2 -14) \cr\cr &=& \dfrac12 (x^2 +2 \cdot 4x+4^2-30) \cr\cr &=& \dfrac12 (x+4)^2 -15 \cr\cr &=& \dfrac12\left( (x+4)^2 -30\right) \end{array}$

Der Scheitelpunkt liegt bei $S(-4 \mid -15)$.

10)
$\begin{array}{rcl} f(x) &=& -x^2+26x-99 \cr &=& -(x^2-26x+99) \cr &=& -(x^2-2 \cdot 13x +13^2 -13^2 +99) \cr &=& -(x^2 -2 \cdot 13x +13^2 -70) \cr &=& -(x-13)^2 +70 \cr &=& -\left((x-13)^2 -70\right) \end{array}$

Der Scheitelpunkt liegt bei $S(13 \mid 70)$.

6. Aufgabe

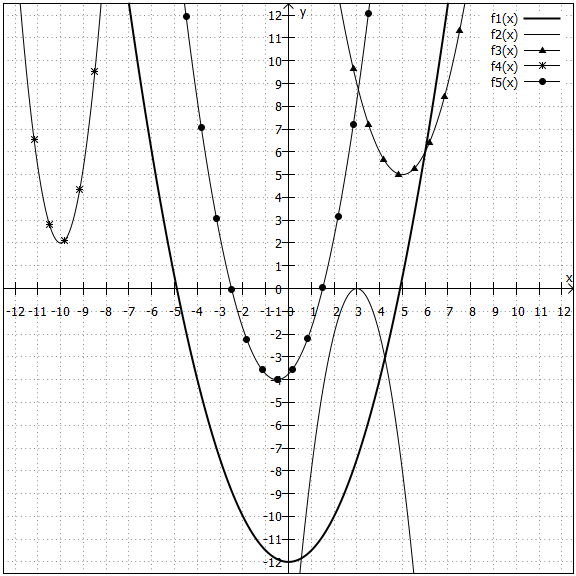
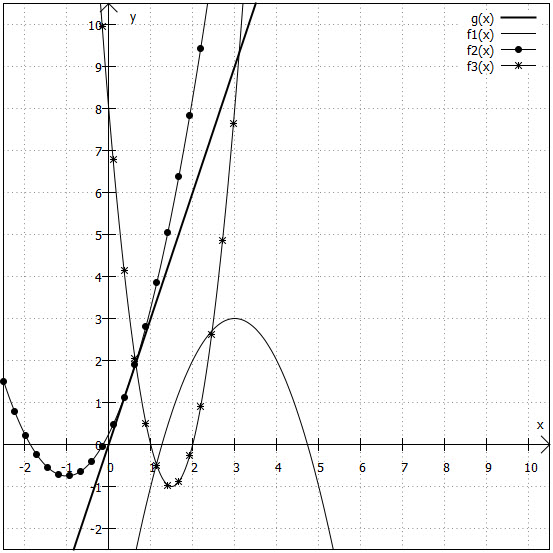
Gerade und Parabel:
1. Möglichkeit: Die Gerade und die Parabel laufen aneinander vorbei. Es gibt also keinen Schnittpunkt, z. B. in der unteren Grafik $g(x)$ und $f_1(x)$.

2. Möglichkeit: Die Gerade und die Parabel berühren sich. Es gibt also einen Schnittpunkt, z. B. in der unteren Grafik $g(x)$ und $f_2(x)$.

3. Möglichkeit: Die Gerade und die Parabel schneiden sich in zwei Punkten, z. B. in der unteren Grafik $g(x)$ und $f_3(x)$.

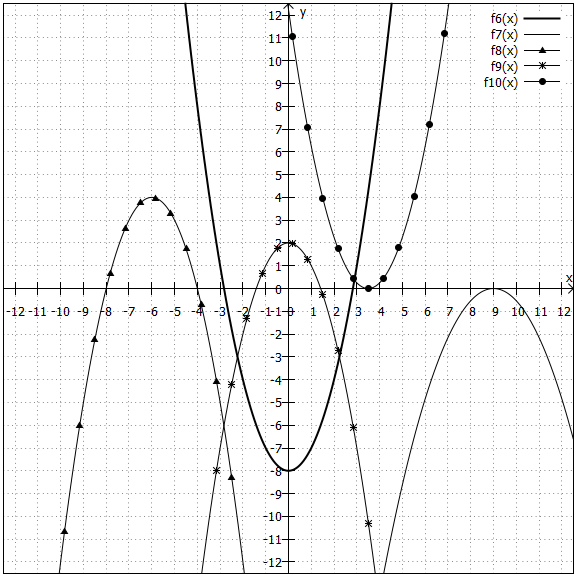
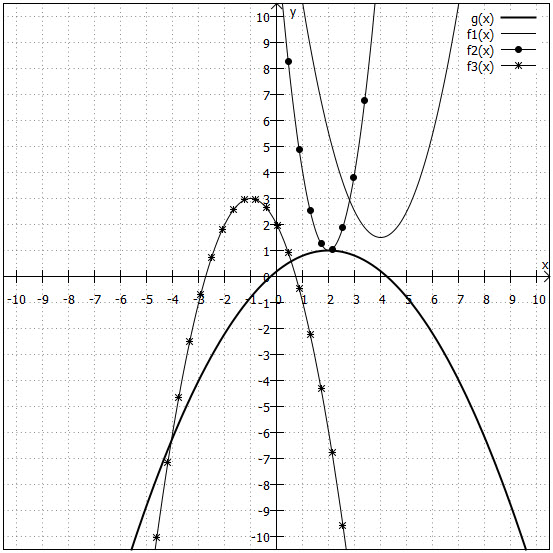
Zwei Parabeln:
1. Möglichkeit: Die beiden Parabeln laufen aneinander vorbei. Es gibt also keinen Schnittpunkt, z. B. in der unteren Grafik $g(x)$ und $f_1(x)$.

2. Möglichkeit: Die beiden Parabeln berühren sich. Es gibt also einen Schnittpunkt, z. B. in der unteren Grafik $g(x)$ und $f_2(x)$.

3. Möglichkeit: Die beiden Parabeln schneiden sich in zwei Punkten, z. B. in der unteren Grafik $g(x)$ und $f_3(x)$.

7. Aufgabe

Vorgehen: Man setzt die beiden Funktionsterme gleich, da die Funktionswerte beider Funktionen gleich sein müssen, damit ein Schnittpunkt vorliegt. Es ergibt sich eine quadratische Gleichung, die (nach etwas Umformen) z. B. mithilfe der p-q-Formel gelöst werden kann.
Anschließend setzt man den ermittelten x-Wert in eine der beiden Funktionsgleichung ein, um den zugehörigen y-Wert zu ermitteln. Es ist egal, in welche Funktionsgleichung der x-Wert eingesetzt wird, da der Punkt ja bei beiden Funktionen identisch sein muss, sonst würden sie sich dort ja nicht schneiden ... Üblicherweise nimmt man daher die einfachere Funktion. Die andere Funktion kann zur Probe genutzt werden.

1)
x-Werte ausrechnen:
$\begin{array}{rclcl} 2x^2-4x+2 &=& \dfrac{1}{2}x+1 & \vert & -\dfrac{1}{2}x -1 \cr 2x^2-\dfrac{9}{2}x+1 &=& 0 & \vert & :2 \cr x^2-\dfrac{9}{4}x+\dfrac{1}{2} &=& 0 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& \dfrac{9}{8} \pm \sqrt{\left(-\dfrac{9}{8}\right)^2-\dfrac{32}{64}} \cr x_{1,2} &=& \dfrac{9}{8} \pm \sqrt{\dfrac{49}{64}} \cr \cr x_1 &=& \dfrac{9}{8}+\dfrac{7}{8} = 2 \cr x_2 &=& \dfrac{9}{8}-\dfrac{7}{8} = \dfrac{1}{4} \end{array}$

y-Werte ausrechnen:
$\begin{array}{rcl}g\left(x_1\right) &=& g\left(2\right) \cr &=& \dfrac{1}{2}\cdot 2+1 \cr &=& 2 \cr\cr g\left(x_2\right) &=& g\left(\dfrac{1}{4}\right) \cr &=& \dfrac{1}{2}\cdot \dfrac{1}{4}+1 \cr &=& \dfrac{9}{8}\end{array}$

Die Schnittpunkte von $f$ und $g$ liegen also bei $S_1 \left( 2 \mid 2 \right)$ und $S_2 \left( \dfrac{1}{4} \mid \dfrac{9}{8} \right)$.

2)
x-Werte ausrechnen:
$\begin{array}{rclcl} -9x^2+8x-1 &=& -10x^2-\dfrac{6}{5}x+7 & \vert & +10x^2+\dfrac{6}{5}x-7 \cr x^2+\dfrac{46}{5}x-8 &=& 0 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& -\dfrac{46}{10} \pm \sqrt{\left(\dfrac{46}{10}\right)^2-(-8)} \cr x_{1,2} &=& -\dfrac{46}{10} \pm \sqrt{\dfrac{2.916}{100}} \cr \cr x_1 &=& -\dfrac{46}{10} + \dfrac{54}{10} = \dfrac{4}{5} \cr x_2 &=& -\dfrac{46}{10} - \dfrac{54}{10} = -10 \end{array}$

y-Werte ausrechnen:
$\begin{array}{rcl}g\left(x_1\right) &=& g\left(\dfrac{4}{5}\right) \cr&=& -9\cdot\left(\dfrac{4}{5}\right)^2+8\cdot\dfrac{4}{5}-1\cr&=& -\dfrac{9}{25} \cr\cr g\left(x_2\right) &=& g\left(-10\right) \cr&=& -9\cdot\left(-10\right)^2+8\cdot\left(-10\right)-1\cr&=& -981\end{array}$

Die Schnittpunkte von $f$ und $g$ liegen also bei $S_1 \left( -10 \mid -981 \right)$ und $S_2 \left( \dfrac{4}{5} \mid -\dfrac{9}{25} \right)$.

3)
x-Werte ausrechnen:
$\begin{array}{rclcl} \dfrac{3}{2}x^2+5x+15 &=& x^2-x-20 & \vert & -x^2+x+20 \cr \dfrac{1}{2}x^2+6x+35 &=& 0 & \vert & \cdot 2 \cr x^2+12x+70 &=& 0 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& -\dfrac{12}{2} \pm \sqrt{\left(\dfrac{12}{2}\right)^2-70} \cr x_{1,2} &=& -6 \pm \sqrt{-34} \end{array}$

Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Gleichung keine Lösung: $f$ und $g$ haben also keine Schnittpunkte.

4)
x-Werte ausrechnen:
$\begin{array}{crclcl} & 4x^2-11 &=& 12x-11 & \vert & -12x+11 \cr & 4x^2-12x &=& 0 \cr & 4x(x-3) &=& 0 & \vert & :4 \cr & x(x-3) &=& 0 & \vert & \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & x_1 &=& 0 \cr\cr \text{Faktor 2:} & x_2-3 &=& 0 & \vert & +3 \cr & x_2 &=& 3 \end{array}$

y-Werte ausrechnen:
$\begin{array}{rcl}g\left(x_1\right) &=& g\left(0\right) \cr&=& 12\cdot 0-11 \cr&=& -11 \cr\cr g\left(x_2\right) &=& g\left(\dfrac{1}{2}\right) \cr&=& 12\cdot 3-11 \cr&=& 25\end{array}$

Die Schnittpunkte von $f$ und $g$ liegen also bei $S_1 \left( 0 \mid -11 \right)$ und $S_2 \left( 3 \mid 25 \right)$.

5)
x-Werte ausrechnen:
$\begin{array}{rclcl} -3x^2-100x+300 &=& -15x^2+20x &\vert & 15x^2-20x \cr 12x^2-120x+300 &=& 0 & \vert & :12 \cr x^2-10x+25 &=& 0 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& \dfrac{10}{2} \pm \sqrt{\left(-\dfrac{10}{2}\right)^2-25} \cr x_{1,2} &=& 5 \pm \sqrt{0} \cr \cr x_1 &=& 5 \end{array}$

y-Werte ausrechnen:
$\begin{array}{rcl}g\left(x_1\right) &=& g\left(5\right) \cr&=& -15\cdot 5^2+20 \cdot 5 \cr&=& -275\end{array}$

Der Schnittpunkt von $f$ und $g$ liegt also bei $S_1 \left( 5 \mid -275 \right)$.

6)
x-Werte ausrechnen:
$\begin{array}{rclcll}-5x^{2} + x + 2 &=& -x^{2} + x + 1 &\vert & +5x^{2} -x -2 \cr 0 &=& 4x^2 - 1 &\vert & +1 \cr 1 &=& 4x^2 &\vert & :4 \cr \dfrac{1}{4} &=& x^2 &\vert & \pm\sqrt{} \cr x_1 &=& \dfrac{1}{2} \cr x_2 &=& -\dfrac{1}{2} \end{array}$

y-Werte ausrechnen:
$\begin{array}{rcl}g\left(x_1\right) &=& g\left(\dfrac{1}{2}\right) \cr&=& -1\cdot\left(\dfrac{1}{2}\right)^2 + 1\cdot\dfrac{1}{2} + 1 \cr &=& \dfrac{5}{4} \cr\cr g\left(x_2\right) &=& g\left(-\dfrac{1}{2}\right) \cr&=& -1\cdot\left(-\dfrac{1}{2}\right)^2 + 1\cdot\left(-\dfrac{1}{2}\right) + 1 \cr &=& \dfrac{1}{4} \end{array}$

Die Schnittpunkte von $f$ und $g$ liegen also bei $S_1 \left(\dfrac{1}{2} \mid \dfrac{5}{4}\right)$ und $S_2 \left(-\dfrac{1}{2} \mid \dfrac{1}{4}\right)$.

7)
x-Werte ausrechnen:
$\begin{array}{crclcll}& -x + 4 &=& -x^2 + 4{,}5x + 4 &\vert & +x^2-4{,}5x-4 \cr & x^2-5{,}5x &=& 0 \cr & x\left(x-5{,}5\right) &=& 0 &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & x_1 &=& 0 \cr\cr \text{Faktor 2:} & x_2-5{,}5 &=& 0 &\vert& +5{,}5 \cr & x_2 &=& 5{,}5 \end{array}$

y-Werte ausrechnen:
$\begin{array}{rcl}f\left(x_1\right) &=& f\left(0\right) \cr&=& -0 + 4 \cr &=& 4 \cr\cr f\left(x_2\right) &=& f\left(5{,}5\right) \cr&=& -5{,}5+ 4 \cr &=& -1{,}5 \end{array}$

Die Schnittpunkte von $f$ und $g$ liegen also bei $S_1 \left(0 \mid 4\right)$ und $S_2 \left(5{,}5 \mid -1{,}5\right)$.

8)
x-Werte ausrechnen:
$\begin{array}{rclcll}1{,}5x^2 + 3x &=&1{,}5x^2 + 10x + 14 &\vert & -1{,}5x^2 -3x \cr0 &=& 7x + 14 &\vert & -14 \cr-14 &=& 7x &\vert & :7 \cr x_1 &=& -2 \end{array}$

y-Wert ausrechnen:
$\begin{array}{rcl}f\left(x_1\right) &=& f\left(-2\right) \cr &=& 1{,}5\cdot\left(-2\right)^2 + 3\cdot\left(-2\right) \cr &=& 0 \end{array}$

Der Schnittpunkt von $f$ und $g$ liegt also bei $S_1 \left(-2 \mid 0\right)$.

9)
x-Werte ausrechnen:
$\begin{array}{rclcll}3x + 7 &=& -x^2 + 10x + 1 &\vert & +x^2-10x-1 \cr x^2-7x+6 &=& 0 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& \dfrac{7}{2} \pm \sqrt{\left(-\dfrac{7}{2}\right)^2- 6} \cr x_{1,2} &=& \dfrac{7}{2} \pm \sqrt{\dfrac{25}{4}} \cr\cr x_1 &=& \dfrac{7}{2} + \dfrac{5}{2} = 6 \cr x_2 &=& \dfrac{7}{2} - \dfrac{5}{2} = 1 \end{array}$

y-Werte ausrechnen:
$\begin{array}{rcl}f\left(x_1\right) &=& f\left(6\right) \cr &=& 3\cdot 6 + 7 \cr &=& 25 \cr\cr f\left(x_2\right) &=& f\left(1\right) \cr &=& 3\cdot 1 + 7 \cr &=& 10 \end{array}$

Die Schnittpunkte von $f$ und $g$ liegen also bei $S_1 \left(1 \mid 10\right)$ und $S_2 \left(6 \mid 25\right)$.

10)
x-Werte ausrechnen:
$\begin{array}{crclcll} & \dfrac12 x^2-13x-15 &=& -8x-15 & \vert & (+8x+15) \cr & \dfrac12 x^2 -5x &=& 0 & \vert & \cdot 2 \cr & x^2-10x &=& 0 & \vert & \text{Satz vom Nullprodukt} \cr & x(x-10) &=& 0 \cr \text{Faktor 1:} & x_1 &=& 0 \cr\cr \text{Faktor 2:} & x_2-10 &=& 0 &\vert& +10 \cr & x_2 &=& 10 \end{array}$

y-Werte ausrechnen:
$\begin{array}{rcl} g(x_1) &=& g(0) \cr &=& -8 \cdot 0 -15 \cr &=& -15\cr\cr g(x_2) &=& g(10) \cr &=& -8 \cdot 10 -15 \cr &=& -95 \end{array}$

Die Schnittpunkte von $f$ und $g$ liegen also bei $S_1 \left( 0 \mid -15 \right)$ und $S_2 \left( 10 \mid -95 \right)$.

8. Aufgabe

1)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} 0 &=& \dfrac{17}{3}\cdot (x^2-4x-221) &\vert& :\dfrac{17}{3} \cr\cr 0 &=& x^2-4x-221 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& 2 \pm \sqrt{\left(-2\right)^2+221} \cr x_{1,2} &=& 2 \pm \sqrt{225} \cr\cr x_1 &=& 2+15 = 17 \cr x_2 &=& 2-15 = -13 \end{array}$

Die Schnittpunkte mit der x-Achse sind also $S_{x1}\left(17 \mid 0\right)$ und $S_{x2}\left(-13 \mid 0\right)$.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& \dfrac{17}{3}\cdot\left(0^2-4\cdot 0-221\right)\\f(0) &=& -\dfrac{3.757}{3} \approx -1.252{,}33\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0 \mid -\dfrac{3.757}{3}\right)$.

2)
Schnittpunkt mit der a-Achse:
$\begin{array}{crclcl} & 0 &=& -\dfrac{1}{4}a^2+a \cr & 0 &=& a \left(-\dfrac{1}{4}a+1\right) & \vert & \text{Satz vom Nullprodukt} \cr\cr \text{Faktor 1:} & a_1 &=& 0 \cr\cr \text{Faktor 2:} & 0 &=& -\dfrac{1}{4}a_2+1 &\vert& -1 \cr & -1 &=& -\dfrac{1}{4}a_2 &\vert& : \left(-\dfrac{1}{4}\right) \cr & a_2 &=& 4 \end{array}$

Die Schnittpunkte mit der a-Achse sind also $S_{a1}\left(0 \mid 0\right)$ und $S_{a2}\left(4 \mid 0\right)$.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& -\dfrac{1}{4}\cdot 0^2+0\\f(0) &=& 0\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0 \mid 0\right)$.

3)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} 0 &=& \left(x+\sqrt{2}\right)^2 &\vert& \sqrt{} \cr 0 &=& x+\sqrt{2} &\vert& -\sqrt{2} \cr x &=& -\sqrt{2} \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_{x}\left(-\sqrt{2} \mid 0\right)$.

Bemerkung: Da auf der linken Seite $0$ steht, dürfen wir hier - ausnahmsweise - beim Wurzelziehen auf das $\pm$ verzichten. $0$ ist ja weder positiv noch negativ.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& \left(0+\sqrt{2}\right)^2\\f(0) &=& 2\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0\;\vert\; 2\right)$.

4)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} 0 &=& -\dfrac{3}{4}x^2+2 &\vert& -2 \cr\cr -2 &=& -\dfrac{3}{4}x^2 &\vert& : \left(-\dfrac{3}{4}\right) \cr\cr x^2 &=& \dfrac{8}{3} &\vert& \pm\sqrt{} \cr\cr x &=& \pm \sqrt{\dfrac{8}{3}} \end{array}$

Die Schnittpunkte mit der x-Achse sind also $S_{x1}\left(\sqrt{\dfrac{8}{3}} \mid 0\right)$ und $S_{x2}\left(-\sqrt{\dfrac{8}{3}} \mid 0\right)$.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& -\dfrac{3}{4}\cdot 0^2+2\\f(0) &=& 2\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0 \mid 2\right)$.

5)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} 0 &=& 3x^2-6x-1 &\vert& :3 \cr 0 &=& x^2-2x-\dfrac{1}{3} &\vert& \text{p-q-Formel} \cr\cr x_{1,2} &=& 1\pm \sqrt{(-1)^2+\dfrac{1}{3}} \cr\cr x_1 &=& 1+\sqrt{\dfrac{4}{3}} \approx 2{,}15 \cr\cr x_2 &=& 1-\sqrt{\dfrac{4}{3}} \approx -0{,}15 \end{array}$

Die Schnittpunkte mit der x-Achse sind also $S_{x1}\left(1+\sqrt{\dfrac{4}{3}} \mid 0\right)$ und $S_{x2}\left(1-\sqrt{\dfrac{4}{3}} \mid 0\right)$.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& 3\cdot 0^2-6\cdot 0 -1 \\f(0) &=& -1\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0 \mid -1\right)$.

6)
Schnittpunkt mit der z-Achse:
$\begin{array}{rclcl} 0 &=& -3z^2+22z-42 &\vert& :(-3) \cr 0 &=& z^2-\dfrac{22}{3}z+14 &\vert& \text{p-q-Formel} \cr\cr z_{1,2} &=& \dfrac{11}{3} \pm \sqrt{\left(-\dfrac{11}{3}\right)^2-14} \cr z_{1,2} &=& \dfrac{11}{3}\pm\sqrt{-\dfrac{5}{9}} \end{array}$

Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Funktion keine Schnittpunkte mit der z-Achse.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& 3\cdot 0^2+22\cdot 0-42 \\f(0) &=& -42\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0 \mid -42\right)$.

7)
Schnittpunkt mit der t-Achse:
$\begin{array}{rclcl} 0 &=& \left(\dfrac{t+17}{\sqrt{2}}\right)^2 &\vert& \sqrt{} \cr\cr 0 &=& \dfrac{t+17}{\sqrt{2}} &\vert& \cdot \sqrt{2} \cr 0 &=& t+17 &\vert& -17 \cr t &=& -17 \end{array}$

Der Schnittpunkt mit der t-Achse ist also $S_{t}\left(-17\;\vert\; 0\right)$.

Bemerkung: Da auf der linken Seite $0$ steht, dürfen wir hier - ausnahmsweise - beim Wurzelziehen auf das $\pm$ verzichten.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& \left(\dfrac{0+17}{\sqrt{2}}\right)^2\\f(0) &=& \dfrac{289}{2} = 144{,}5\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0\;\vert\; \dfrac{289}{2}\right)$.

8)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} 0 &=& x^2+4x-5 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& -2 \pm \sqrt{2^2+5} \cr &=& -2 \pm \sqrt{9} \cr\cr x_1 &=& -2+3 = 1 \cr x_2 &=& -2-3 = -5 \end{array}$

Die Schnittpunkte mit der x-Achse sind also $S_{x1}\left(1 \mid 0\right)$ und $S_{x2}\left(-5 \mid 0\right)$.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& 0^2+4\cdot 0-5\\f(0) &=& -5\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0 \mid -5\right)$.

9)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} 0 &=& \dfrac{a-1}{3}x^2-a &\vert& -\dfrac{a-1}{3}x^2 \cr\cr -\dfrac{a-1}{3}x^2 &=& -a &\vert& \cdot (-3) \cr\cr (a-1)x^2 &=& 3a &\vert& :(a-1) \cr x^2 &=& \dfrac{3a}{a-1} \cr\cr x_{1,2} &=& \pm \sqrt{\dfrac{3a}{a-1}} \end{array}$

Die Schnittpunkte mit der x-Achse sind also $S_{x1}\left(-\sqrt{\dfrac{3a}{a-1}} \mid 0\right)$ und $S_{x2}\left(\sqrt{\dfrac{3a}{a-1}} \mid 0\right)$.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& \dfrac{a-1}{3}\cdot 0^2-a\\f(0) &=& -a\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0 \mid -a\right)$.

Bemerkung: Wie immer, wenn ein Parameter in einer Aufgabe enthalten ist, wie hier das $a$, sollte man kurz überlegen, ob es Werte von $a$ gibt, bei denen sich die Funktion anders verhält als sonst, bzw. Werte, die $a$ nicht annehmen darf, wenn die Rechnung funktionieren soll. Schaut man sich den Funktionsterm von $f(x)$ an, stellt man fest, dass die Funktion bei $a=1$ nicht mehr quadratisch ist: Für $a=1$ würde der Funktionsterm nämlich zu $f(x) = \dfrac{1-1}{3}x^2-1 = 0x^2-1 = -1$. Da erübrigt sich die Suche nach den Schnittpunkten mit der x-Achse ...
Problematisch wird $a=1$ auch dort, wo durch $a-1$ geteilt werden muss, denn $1-1$ ist ja nun mal $0$.
Bei allen anderen Werten passiert das nicht: Die Funktion bleibt quadratisch und teilen dürfen wir auch. Halten wir also fest: $a\in\mathbb{R}\setminus_{\{1\}}$

10)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} 0 &=& 3x^2+(6-6r)x-12r \cr 0 &=& 3x^2+6(1-r)x-12r &\vert& :3 \cr 0 &=& x^2+2(1-r)x-4r &\vert& \text{p-q-Formel} \cr x_{1,2} &=& -\dfrac{2(1-r)}{2} \pm \sqrt{(1-r)^2+4r} \cr x_{1,2} &=& -(1-r) \pm \sqrt{1-2r+r^2+4r} \cr x_{1,2} &=& -1+r \pm \sqrt{r^2+2r+1} \cr x_{1,2} &=& -1+r \pm \sqrt{(r+1)^2} \cr\cr x_1 &=& -1+r+r+1 = 2r \cr x_2 &=& -1+r-r-1 = -2 \end{array}$

Die Schnittpunkte mit der x-Achse sind also $S_{x1}\left(2r \mid 0\right)$ und $S_{x2}\left(-2 \mid 0\right)$.

Schnittpunkt mit der y-Achse:
$\begin{array}{rclcll}f(0) &=& 3\cdot 0^2+\left(6-6r\right)\cdot 0-12r\\f(0) &=& -12r\end{array}$

Der Schnittpunkt mit der y-Achse ist also $S_{y}\left(0 \mid -12r\right)$.

Bemerkung: Auch hier noch eine kurze Überlegung zum Parameter $r$: Für $r$ gibt es keine Einschränkungen - aus zwei Gründen.
1. $r$ hat nur Auswirkungen auf den linearen und konstanten Teil des Funktionsterms. Das ist problemlos, da sowohl der Koeffizient des linearen Terms als auch der konstante Term jeden Wert (einschließlich $0$) annehmen dürfen.
2. Es wird nirgends durch $r$ geteilt oder die Wurzel aus $r$ gezogen. Dort, wo $r$ unter der Wurzel steht, lässt sich der Radikand zu $(r+1)^2$ umformen, was immer nichtnegativ ist. Hier können also auch keine Probleme entstehen.
Zusammengefasst: $r\in\mathbb{R}$

9. Aufgabe

Wir beginnen einfach mal so, wie man immer beginnt, wenn man Nullstellen berechnen möchte:
$\begin{array}{rclcll}0 &=& 2x^2+ax-1 &\vert& :2 \cr0 &=& x^2+\dfrac{a}{2}x-\dfrac12 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& -\dfrac{a}{4}\pm\sqrt{\left(\dfrac{a}{4}\right)^2+\dfrac12} \cr x_{1,2} &=& -\dfrac{a}{4}\pm\sqrt{\dfrac{a^2}{16}+\dfrac{8}{16}} \cr x_{1,2} &=& -\dfrac{a}{4}\pm\sqrt{\dfrac{a^2+8}{16}} \cr x_{1,2} &=& \dfrac{-a\pm\sqrt{a^2+8}}{4}\end{array}$

a)
Die Funktion hat genau eine Nullstelle, wenn der Wurzelterm in der letzten Zeile der Rechnung oben $0$ ist:
$\begin{array}{crclcl} \sqrt{a^2+8} &=& 0 \cr a^2+8 &=& 0 \cr a^2 &=& -8\end{array}$

Da Quadrate niemals negativ sein können, gibt es keinen Wert für $a$, bei dem der Wurzelterm $0$ ist. Die Funktion $f(x)$ kann also nicht genau eine Nullstelle haben.

b)
Die Parabel schneidet die y-Achse im Punkt $(0\mid -1)$ (kann man einfach ausrechnen, indem man $x=0$ in die Funktionsgleichung einsetzt) und ist nach oben geöffnet (der Koeffizient vor $x^2$ ist ja positiv). Daher besitzt sie immer genau zwei Nullstellen. Es gibt deswegen keinen Wert für $a$, für den die Funktion $f(x)$ keine Nullstelle hat.

Anmerkung: Wer gleich so argumentiert wie bei b), kann sich die Rechnung bei a) sparen ...

10. Aufgabe

Vorbemerkung: Für quadratische Funktionen gilt immer $f(x)=ax^2+bx+c$ mit $a,b,c \in\mathbb{R}$. Normalerweise kennen wir $a$, $b$ und $c$ schon - diesmal müssen wir sie bestimmen. Was wir stattdessen kennen, sind die Funktionswerte von $f(x)$ für die Punkte $P_1$, $P_2$ und $P_3$. Damit können wir starten.

1)
Wir beginnen damit, die gegebenen Punkte in die allgemeine Funktionsgleichung einzusetzen:
$\begin{array}{lcrcrcrcr} f(0) &=& a\cdot 0^2 &+& b\cdot 0 &+& c &=& -16 \cr f(1) &=& a\cdot 1^2 &+& b\cdot 1 &+& c &=& -10 \cr f(3) &=& a\cdot 3^2 &+& b\cdot 3 &+& c &=& 14 \end{array}$

Etwas vereinfacht und zusammengefasst erhalten wir ein lineares Gleichungssystem mit den Variablen $a$, $b$ und $c$:
$\begin{array}{crcrcrcr} \text{I} & & & & & c &=& -16 \cr \text{II} & a &+& b &+& c &=& -10 \cr \text{III} & 9a &+& 3b &+& c &=& 14 \end{array}$

In Zeile I müssen wir gar nicht rechnen, sondern sehen sofort $c=-16$. Das setzen wir im nächsten Schritt in die anderen Zeilen ein, damit das lineare Gleichungssystem handlicher wird, nämlich:
$\begin{array}{crcrcrcrcl} \text{II} & a &+& b &-& 16 &=& -10 &\vert& +16 \cr \text{III} & 9a &+& 3b &-& 16 &=& 14 &\vert& +16 \cr \cr \text{II} & a &+& b & & &=& 6 \cr \text{III} & 9a &+& 3b & & &=& 30 \end{array}$

Nun ist ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten entstanden, welches z. B. mithilfe des Einsetzungsverfahrens gelöst werden kann:
$\begin{array}{crcrcl} \text{II} & a+b &=& 6 &\vert& -b \cr \text{III} & 9a+3b &=& 30 \cr \cr \text{II} & a &=& 6-b \cr \text{III} & 9a+3b &=& 30 \cr \cr \text{II in III} & 9(6-b)+3b &=& 30 \cr & 54-9b+3b &=& 30 \cr & 54-6b &=& 30 &\vert& -54 \cr & -6b &=& -24 &\vert& :\left(-6\right) \cr & b &=& 4 \cr \cr \text{b in II} & a &=& 6-4 \cr & a &=& 2 \end{array}$

Das Gleichungssystem hat also die Lösung $a=2$, $b=4$ und $c=-16$. Um die gesuchte quadratische Funktion zu bestimmen, setzen wir diese Werte nun in die allgemeine Funktionsgleichung ein: $f(x)=2x^2+4x-16$

Wer möchte, kann zur Probe die gegebenen Punkte in die gefundene Funktionsgleichung einsetzen:
$\begin{array}{rclcl}f(0) &=& 2\cdot 0^2+4\cdot 0-16 &=& -16 \cr f(1) &=& 2\cdot 1^2+4\cdot 1-16 &=& -10 \cr f(3) &=& 2\cdot 3^2+4\cdot 3-16 &=& 14 \end{array}$

Alles richtig!

2)
Wir beginnen damit, die gegebenen Punkte in die allgemeine Funktionsgleichung einzusetzen:
$\begin{array}{lcrcrcrcr} f(2) &=& a\cdot 2^2 &+& b\cdot 2 &+& c &=& 1 \cr f(1) &=& a\cdot 1^2 &+& b\cdot 1 &+& c &=& 2 \cr f(0) &=& a\cdot 0^2 &+& b\cdot 0 &+& c &=& 1 \end{array}$

Etwas vereinfacht und zusammengefasst erhalten wir ein lineares Gleichungssystem mit den Variablen $a$, $b$ und $c$:
$\begin{array}{crcrcrcr} \text{I} & 4a &+& 2b &+& c &=& 1 \cr \text{II} & a &+& b &+& c &=& 2 \cr \text{III} & & & & & c &=& 1 \end{array}$

In Zeile III müssen wir gar nicht rechnen, sondern sehen sofort $c=1$. Das setzen wir im nächsten Schritt in die anderen Zeilen ein, damit das lineare Gleichungssystem handlicher wird, nämlich:
$\begin{array}{crcrcrcrcl} \text{I} & 4a &+& 2b &+& 1 &=& 1 &\vert& -1 \cr \text{II} & a &+& b &+& 1 &=& 2 &\vert& -1 \cr \cr \text{I} & 4a &+& 2b & & &=& 0 \cr \text{II} & a &+& b & & &=& 1 \end{array}$

Nun ist ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten entstanden, welches z. B. mithilfe des Einsetzungsverfahrens gelöst werden kann:
$\begin{array}{crcrcl} \text{I} & 4a+2b &=& 0 \cr \text{II} & a+b &=& 1 &\vert& -b \cr \cr \text{I} & 4a+2b &=& 0 \cr \text{II} & a &=& 1-b \cr \cr \text{II in I} & 4(1-b)+2b &=& 0 \cr & 4-4b+2b &=& 0 \cr & 4-2b &=& 0 &\vert& -4 \cr & -2b &=& -4 &\vert& :\left(-2\right) \cr & b &=& 2 \cr \cr \text{b in II} & a &=& 1-2 \cr & a &=& -1 \end{array}$

Das Gleichungssystem hat also die Lösung $a=-1$, $b=2$ und $c=1$. Um die gesuchte quadratische Funktion zu bestimmen, setzen wir diese Werte nun in die allgemeine Funktionsgleichung ein: $f(x)=-x^2+2x+1$

Die Probe:
$\begin{array}{rclcl}f(2) &=& -2^2+2\cdot 2+1 &=& 1 \cr f(1) &=& -1^2+2\cdot 1+1 &=& 2 \cr f(0) &=& -0^2+2\cdot 0+1 &=& 1 \end{array}$

Alles richtig!

3)
Wir beginnen damit, die gegebenen Punkte in die allgemeine Funktionsgleichung einzusetzen:
$\begin{array}{lcrcrcrcr} f(0) &=& a\cdot 0^2 &+& b\cdot 0 &+& c &=& 0 \cr f\left(\dfrac{1}{3}\right) &=& a\cdot \left(\dfrac{1}{3}\right)^2 &+& b\cdot \dfrac{1}{3} &+& c &=& -\dfrac{1}{3} \cr f\left(\dfrac{2}{3}\right) &=& a\cdot \left(\dfrac{2}{3}\right)^2 &+& b\cdot \dfrac{2}{3} &+& c &=& 0 \end{array}$

Etwas vereinfacht und zusammengefasst erhalten wir ein lineares Gleichungssystem mit den Variablen $a$, $b$ und $c$:
$\begin{array}{crcrcrcr} \text{I} & & & & & c &=& 0 \cr \text{II} & \dfrac{1}{9}a &+& \dfrac{1}{3}b &+& c &=& -\dfrac{1}{3} \cr \text{III} & \dfrac{4}{9}a &+& \dfrac{2}{3}b &+& c &=& 0 \end{array}$

In Zeile I müssen wir gar nicht rechnen, sondern sehen sofort $c=0$. Das setzen wir im nächsten Schritt in die anderen Zeilen ein, damit das lineare Gleichungssystem handlicher wird, nämlich:
$\begin{array}{crcrcrcrcl} \text{II} & \dfrac{1}{9}a &+& \dfrac{1}{3}b &+& 0 &=& -\dfrac{1}{3} \cr \text{III} & \dfrac{4}{9}a &+& \dfrac{2}{3}b &+& 0 &=& 0 \cr \cr \text{II} & \dfrac{1}{9}a &+& \dfrac{1}{3}b & & &=& -\dfrac{1}{3} \cr \text{III} & \dfrac{4}{9}a &+& \dfrac{2}{3}b & & &=& 0 \end{array}$

Nun ist ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten entstanden, welches z. B. mithilfe des Additionsverfahrens gelöst werden kann:
$\begin{array}{crclllcc} \text{II} & \dfrac{1}{9}a+\dfrac{1}{3}b &=& -\dfrac{1}{3} &\vert& \cdot (-2)\cr \text{III} & \dfrac{4}{9}a+\dfrac{2}{3}b &=& 0 \cr\cr \text{II} & -\dfrac{2}{9}a-\dfrac{2}{3}b &=& \dfrac{2}{3} \cr \text{III} & \dfrac{4}{9}a+\dfrac{2}{3}b &=& 0 \cr\cr \text{II+III} & \dfrac{2}{9}a-0b &=& \dfrac{2}{3} \cr & \dfrac{2}{9}a &=& \dfrac{2}{3} &\vert& : \dfrac{2}{9} \cr & a &=& 3 \cr\cr \text{a in III} & \dfrac{4}{9}\cdot 3+\dfrac{2}{3}b &=& 0 &\vert& -\dfrac{4}{3} \cr & \dfrac{2}{3}b &=& -\dfrac{4}{3} &\vert& :\dfrac{2}{3} \cr & b &=& -2 \end{array}$

Das Gleichungssystem hat also die Lösung $a=3$, $b=-2$ und $c=0$. Um die gesuchte quadratische Funktion zu bestimmen, setzen wir diese Werte nun in die allgemeine Funktionsgleichung ein: $f(x)=3x^2 - 2x$

Die Probe:
$\begin{array}{rclcl}f(0) &=& 3\cdot 0^2 - 2\cdot 0 &=& 0 \cr f\left(\dfrac{1}{3}\right) &=& 3\cdot\left(\dfrac{1}{3}\right)^2 - 2\cdot\dfrac{1}{3} &=& -\dfrac{1}{3} \cr f\left(\dfrac{2}{3}\right) &=& 3\cdot\left(\dfrac{2}{3}\right)^2 - 2\cdot\dfrac{2}{3} &=& 0 \end{array}$

Alles richtig!

4)
Wir beginnen damit, die gegebenen Punkte in die allgemeine Funktionsgleichung einzusetzen:
$\begin{array}{lcrcrcrcr} f(4) &=& a\cdot 4^2 &+& b\cdot 4 &+& c &=& 3 \cr f(2) &=& a\cdot 2^2 &+& b\cdot 2 &+& c &=& 0 \cr f(-5) &=& a\cdot \left(-5\right)^2 &+& b\cdot (-5) &+& c &=& 5{,}25 \end{array}$

Etwas vereinfacht und zusammengefasst erhalten wir ein lineares Gleichungssystem mit den Variablen $a$, $b$ und $c$:
$\begin{array}{crcrcrcr} \text{I} & 16a &+& 4b &+& c &=& 3 \cr \text{II} & 4a &+& 2b &+& c &=& 0 \cr \text{III} & 25a &-& 5b &+& c &=& 5{,}25\end{array}$

Hier tut uns leider keine der Gleichungen den Gefallen, die Lösung sofort bereit zu halten. Wir müssen das Gleichungssystem (drei Gleichungen mit drei Unbekannten) also klassisch mit dem Additionsverfahren lösen:
$\begin{array}{crcrcrcrl} \text{I} & 16a &+& 4b &+& c &=& 3 \cr \text{II} & 4a &+& 2b &+& c &=& 0 \cr \text{III} & 25a &-& 5b &+& c &=& 5{,}25 \cr \cr \text{I} & 16a &+& 4b &+& c &=& 3 \cr \text{I-II} & 12a &+& 2b & & &=& 3 \cr \text{I-III} & -9a &+& 9b & & &=& -2{,}25 \cr \cr \text{I} & 16a &+& 4b &+& c &=& 3 \cr \text{II'} & 12a &+& 2b & & &=& 3 \cr \text{3 II'+4 III'} & & & 42b & & &=& 0 & \Rightarrow b = 0 \cr \cr b = 0 \text{ in II'} & 12a &+& 2\cdot 0 & & &=& 3 & \Rightarrow a = \dfrac{1}{4} \cr b = 0 \text{ und } a = \dfrac{1}{4} \text{ in II} & 4\cdot\dfrac{1}{4} &+& 2 \cdot 0 &+& c &=& 0 & \Rightarrow c = -1 \end{array}$

Das Gleichungssystem hat also die Lösung $a=\dfrac{1}{4}$, $b=0$ und $c=-1$. Um die gesuchte quadratische Funktion zu bestimmen, setzen wir diese Werte nun in die allgemeine Funktionsgleichung ein: $f(x)=\dfrac{1}{4}x^2 - 1$

Die Probe:
$\begin{array}{rclcl}f(4) &=& \dfrac{1}{4} \cdot 4^2 - 1 &=& 3 \cr f(2) &=& \dfrac{1}{4} \cdot 2^2 - 1 &=& 0 \cr f(-5) &=& \dfrac{1}{4} \cdot (-5)^2 - 1 &=& 5{,}25 \end{array}$

Alles richtig!

5)
Wir beginnen damit, die angegebenen Punkte in die allgemeine Funktionsgleichung einzusetzen:
$\begin{array}{lcrcrcrcr} f(-1) &=& a \cdot (-1)^2 &+& b \cdot (-1) &+& c &=& 2 \cr f(0) &=& a \cdot 0^2 &+& b \cdot 0 &+& c &=& 4 \cr f(2) &=& a \cdot 2^2 &+& b \cdot 2 &+& c &=& 12 \end{array}$

Etwas vereinfacht und zusammengefasst erhalten wir ein lineares Gleichungssystem mit den Variablen $a$, $b$ und $c$:
$\begin{array}{crcrcrcr} \text{I} & a &-& b &+& c &=& 2 \cr \text{II} & & & & & c &=& 4 \cr \text{III} & 4a &+& 2b &+& c &=& 12 \end{array}$

In Zeile $\text{II}$ müssen wir gar nicht rechnen, sondern sehen sofort $c=4$. Das setzen wir im nächsten Schritt in die anderen beiden Zeilen ein, damit das lineare Gleichungssystem handlicher wird, nämlich:
$\begin{array}{crcrcrcrcl} \text{I} & a &-& b &+& 4 &=& 2 &\vert& -4 \cr \text{III} & 4a &+& 2b &+& 4 &=& 12 &\vert& -4 \cr\cr \text{I} & a &-& b & & &=& -2 \cr \text{III} & 4a &+& 2b & & &=& 8 \end{array}$

Nun ist ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten entstanden, welches z. B. mithilfe des Einsetzungsverfahrens gelöst werden kann:
$\begin{array}{crcrcl} \text{I} & a - b &=& -2 &\vert& +b \cr \text{III} & 4a + 2b &=& 8 \cr\cr \text{I} & a &=& -2 + b \cr \text{III} & 4a + 2b &=& 8 \cr \cr \text{I in III} & 4\left(-2 +b \right) +2b &=& 8 \cr & -8 + 4b + 2b &=& 8 &\vert& +8 \cr & 6b &=& 16 &\vert& :6 \cr & b &=& \dfrac{8}{3} \cr\cr \text{b in I} & a &=& -2 + \dfrac83 \cr & a &=& \dfrac{2}{3} \end{array}$

Das Gleichungssystem hat also die Lösung $a=\dfrac23$, $b=\dfrac83$ und $c=4$. Um die gesuchte quadratische Gleichung zu bestimmen, setzen wir diese Werte nun in die allgemeine Funktionsgleichung ein: $f(x)=\dfrac23 x^2 + \dfrac83 x + 4$

Die Probe:
$\begin{array}{rclcl} f(-1) &=& \dfrac23 \cdot (-1)^2 + \dfrac83 \cdot (-1) +4 &=& 2 \cr\cr f(0) &=& \dfrac23 \cdot 0^2 + \dfrac83 \cdot 0 + 4 &=& 4 \cr\cr f(2) &=& \dfrac23 \cdot 2^2 + \dfrac83 \cdot 2 + 4 &=& 12 \end{array}$

Alles richtig!