Dieses Kapitel enthält die folgenden Themen:

• Definition
• Exponentialgleichungen
• Exponentialfunktionen

16.2 Exponentialgleichungen und -funktionen - Erklärungen

Im Kapitel Polynomgleichungen und -funktionen haben wir uns Gleichungen und Funktionen angeschaut, bei denen die Variable in der Basis eines Potenzterms steht. Möglich ist aber natürlich auch, dass die Variable im Exponenten steht. Diese sogenannten Exponentialgleichungen bzw. -funktionen spielen in ganz unterschiedlichen Kontexten eine wichtige Rolle. Charakteristisch für diesen Gleichungs- und Funktionstyp sind Vorgänge, bei denen sich in gleich großen Intervallen der Wert um den gleichen Faktor ändert. Beispiele dafür sind:

• Wachstumsvorgänge, z. B. bei Bakterien oder der Zinsentwicklung: Dabei ist die Basis größer als $1$. Man sagt in diesem Fall auch "exponentielles Wachstum".
• Zerfallsprozesse, z. B. bei radioaktiven Materialien: Hierbei tritt eine Basis zwischen $0$ und $1$ auf.

Auch in der Wahrscheinlichkeitsrechnung und bei Differentialgleichungen trifft man auf Exponentialgleichungen bzw. Exponentialfunktionen.
Wie schon im vorherigen Kapitel gilt auch hier: Wer sich (noch) nicht mit den Rechenregeln für Potenzen und Co. vertraut gemacht hat, sollte dies nun nachholen. Wir werden diese Rechenregeln und -gesetze im nun folgenden Kapitel brauchen.

Definition

Definition einer Exponentialgleichung: Exponentialgleichungen sind Gleichungen, bei denen die Variable als Exponent einer konstanten Basis $a$ mit $a\in\mathbb{R}^+\setminus_{\{1\}}$ auftritt.
Definition einer Exponentialfunktion: Exponentialfunktionen sind Funktionen, bei denen die Variable als Exponent einer konstanten Basis $a$ mit $a\in\mathbb{R}^+\setminus_{\{1\}}$ auftritt.

Definitionsbereich: Der Definitionsbereich von Exponentialgleichungen und Exponentialfunktionen umfasst die gesamten reellen Zahlen.

Exkurs: Schauen wir uns an, warum für die Basis nur positive reelle Zahlen mit Ausnahme der $1$ zugelassen sind:
$1$ als Basis einer Exponentialgleichung oder -funktion wäre eine ziemlich langweilige Angelegenheit, denn $1^x = 1$, egal für welche reelle Zahl die Variable $x$ steht. Wenn man die Konstante $1$ mal braucht, kann man sie ja einfach so hinschreiben, ohne Potenz ...
Ähnlich ist es mit der Basis $0$: $0^x = 0$ für alle reellen Zahlen $x$ mit Ausnahme von $x=0$. $0^0$ ist nämlich nicht definiert, sodass wir in diesem Fall den Definitionsbereich einschränken müssten. Diese Mühe lohnt sich nicht, wenn mit der Funktion ansonsten sowieso nichts passiert ...
Negative Basen würden uns insofern Schwierigkeiten machen, da gebrochene Exponenten (die laut Definitionsbereich zulässig sind) ja zu Wurzeltermen führen. Ein solcher Wurzelterm hätte einen negativen Radikanden, was in Kombination mit einem geraden Wurzelexponenten im Bereich der reellen Zahlen nicht berechnet werden kann. Man hätte bei negativen Basen also den Fall, dass einige Kombinationen von Basis und Exponent funktionieren ($(-3)^2 = 9$) und andere nicht ($(-3)^{\frac{1}{2}} = \sqrt[2]{-3}$). Da das nicht sinnvoll ist, schließt man negative Basen bei Exponentialgleichungen oder -funktionen grundsätzlich aus.

Ganz wichtig: Bitte beachten Sie den Unterschied zwischen Polynomen und Exponentialgleichungen/-funktionen: Während wir uns in diesem Kapitel um Gleichungen und Funktionen kümmern, bei denen die unabhängige Variable im Exponenten steht, ist es bei Polynomen die Basis, die variabel ist.

Exponentialgleichungen

Auch in diesem Kapitel einige Beispiele zum Start:

• $e^{8x+2} = 119$
  Die eulersche Zahl $e$ ist eine typische Basis für Exponentialgleichungen.
  
  
• $10.240 = 10\cdot 2^{x-3}$
  
  
• $10^{y^2-10} \cdot 100^{y} = 10^{y-7}$

Lösungsweg

Einige Exponentialgleichungen sind nur auf den ersten Blick wirklich schwierig. Häufig lassen sie sich nämlich mit wenigen Umformungen auf einfache Polynomgleichungen zurückführen. Logarithmieren als eine Umkehroperation zum Potenzieren hilft auf dem Weg zur Lösung oft weiter. Grundsätzlich ist es immer eine gute Idee, die Bestandteile der Gleichung zunächst so weit wie möglich zusammenzufassen. Dabei helfen u. a. die Potenz- und Logarithmengesetze.
Zur Lösbarkeit von Exponentialgleichungen kann man leider nicht so präzise Aussagen machen, weil dies ganz stark von der Struktur der Gleichung abhängt. Wie auch bei Polynomgleichungen ist es möglich, dass Exponentialgleichungen nur numerisch lösbar sind. Dies passiert vor allem dann, wenn eine Gleichung Exponentialterme und zugleich Polynome enthält, z. B. $e^{2x} \cdot e^6 = x+12$. Um die Exponentialterme auf der linken Seite aufzulösen, müsste man die Gleichung logarithmieren - dann würden aber auf der rechten Seite Logarithmusterme entstehen, sodass man exponenzieren müsste. Das würde aber direkt wieder zur Ausgangsgleichung führen. Daher bleiben in solchen Fällen bloß numerische Verfahren, um eine Lösung zu finden. Dieses Thema werden wir in diesem Lernmodul aber nicht behandeln. Das wird im Studium thematisiert werden, wenn Sie es benötigen.

Zur Schreibweise: Mit $\ln()$ hinter dem senkrechten Strich am Ende einer Zeile ist gemeint, dass der natürliche Logarithmus auf beiden Seiten der Gleichung angewendet wird; analog für Logarithmen zu anderen Basen.

Schauen wir uns - wie schon in den vorangegangenen Kapiteln - einige Beispiele an:

Beispiel 1:
$\begin{array}{crclcl} & \mathbb{D} &=& \mathbb{R} \cr \cr \text{1. Zeile:} & 1{,}1^{x+1} &=& 1{,}2^x &\vert& \ln() \cr \text{2. Zeile:} & \ln\left(1{,}1^{x+1}\right) &=& \ln\left(1{,}2^x\right) \cr \text{3. Zeile:} & (x+1)\ln(1{,}1) &=& x\ln(1{,}2) \cr & x\ln(1{,}1)+\ln(1{,}1) &=& x\ln(1{,}2) &\vert&\ -\ln(1{,}1)-x\ln(1{,}2) \cr & x\ln(1{,}1)-x\ln(1{,}2) &=& -\ln(1{,}1) \cr & x\left(\ln(1{,}1)-\ln(1{,}2)\right) &=& -\ln(1{,}1) &\vert& : \left(\ln(1{,}1)-\ln(1{,}2)\right) \cr & x &=& -\dfrac{\ln(1{,}1)}{\ln(1{,}1)-\ln(1{,}2)} \cr \cr & \mathbb{L} &=& \left\{-\dfrac{\ln(1{,}1)}{\ln(1{,}1)-\ln(1{,}2)}\right\} \end{array}$

Zur 1. Zeile: Die Gleichung wird logarithmiert. Das ist bei vielen Exponentialgleichungen, die nur Exponentialterme enthalten, eine gute Idee. Ob man dabei lieber mit dem natürlichen Logarithmus oder einem Logarithmus zu einer anderen Basis rechnet, hat keinen Einfluss auf das Ergebnis. Wichtig ist hingegen, dass auf beiden Seiten der Gleichung logarithmiert wird - so wie es bei linearen Gleichungen wichtig ist, beim Multiplizieren mit einem Faktoren immer beide Seiten der Gleichung zu berücksichtigen.

Zur 2. Zeile: In diesem Schritt wird das 3. Logarithmengesetz angewendet. Achten Sie dabei auf der linken Seite unbedingt darauf, den Exponenten in Klammern zu setzen, weil er ja aus einer Summe besteht, die als Ganzes multipliziert werden soll.

Ab der 3. Zeile: Auch wenn es vielleicht auf den ersten Blick überrascht, ist die Gleichung nun linear. $\ln(1{,}1)\approx 0{,}0953$ und $\ln(1{,}2)\approx 0{,}1823$ sind nämlich einfach nur Zahlen, wenn sie auch erstmal nicht so aussehen ...
Der restliche Lösungsweg verläuft so wie bei anderen linearen Gleichungen auch: Klammer auf der linken Seite der Gleichung ausmultiplizieren - Terme sortieren - auf der linken Seite $x$ ausklammern - durch den Koeffizienten von $x$ teilen - fertig!

Bemerkung: $-\frac{\ln(1{,}1)}{\ln(1{,}1)-\ln(1{,}2)} \approx 1{,}095$
Warum ist das Ergebnis positiv, wo doch ein Minuszeichen vor dem Bruch steht? Ohne genaue Zahlenwerte für die Logarithmen zu ermitteln, kann man sich Folgendes überlegen: Der Logarithmus ist eine Funktion, bei der größere Argumente zu größeren Funktionswerten führen (Mathematisch sagt man: Die Funktion ist streng monoton steigend.). Da $\ln(1)=0$ ist, muss $\ln(1{,}1)$ etwas größer als $0$ sein. Außerdem muss $\ln(1{,}2)$ etwas größer als $\ln(1{,}1)$ sein (die beiden genauen Werte stehen weiter oben - aber ganz genau braucht man die für diese Überlegungen gar nicht). Daraus folgt, dass im Nenner des Bruches eine negative Zahl steht. Da der Zähler positiv ist, ist der gesamte Bruch also negativ. Zusammen mit dem Minuszeichen davor ergibt sich also ein positiver Wert.
Man kann natürlich auch den Taschenrechner fragen ...

Beispiel 2:
$\begin{array}{ccrclcl}& & \mathbb{D} &=& \mathbb{R} \\\\\text{1. Zeile:} & & \dfrac{2}{e^{-x+1}} \left(x^2-x\right) &=& 40e^{x-1} \\\\\text{2. Zeile:} & & 2\left(x^2-x\right)e^{-(-x+1)} &=& 40e^{x-1} \\\\\text{3. Zeile:} & & \left(2x^2-2x\right)e^{x-1} &=& 40e^{x-1} & \vert & -40e^{x-1} \\\\\text{4. Zeile:} & & \left(2x^2-2x\right)e^{x-1}-40e^{x-1} &=& 0 \\\\\text{5. Zeile:} & & e^{x-1}\left(2x^2-2x-40\right) &=& 0 &\vert& \text{Satz vom Nullprodukt}\\\\\text{6. Zeile:} & \text{Faktor 1:} & e^{x-1} &=& 0 \\\\\\\text{7. Zeile:} & \text{Faktor 2:} & 2x^2-2x-40 &=& 0 & \vert& :2 \\\\& & x^2-x -20 &=& 0 & \vert& \text{p-q-Formel} \\\\& & x_{1,2}&=&\dfrac{1}{2}\pm\sqrt{\left(-\dfrac{1}{2}\right)^2+20}\\\\& & x_{1,2}&=&\dfrac{1}{2}\pm\sqrt{\dfrac{81}{4}}\\\\& & x_{1}&=&\dfrac{1}{2}+\dfrac{9}{2} = 5 \\\\ & & x_{2}&=&\dfrac{1}{2}-\dfrac{9}{2} = -4 \\\\\\& & \mathbb{L} &=& \{-4;5\}\end{array}$

Zur 1. Zeile: Zunächst vereinfachen wir die Gleichung, weil der Term $e^{-x+1}$ im Nenner ungünstig ist. Um den Term in den Zähler zu ziehen, müssen wir den Exponenten mit $-1$ multiplizieren. Dies hatten wir uns im Kapitel Potenzen, Wurzeln, Logarithmen angeschaut. Angenehme Folge: Wir können nun ohne Bruch weiterrechnen.

Zur 2. Zeile: Nun wird die Minusklammer im Exponenten aufgelöst und man erhält $e^{x-1}$. Außerdem werden die $2$ und die Klammer vor dem Exponentialterm zusammengefasst (Distributivgesetz).

Zur 3. Zeile: Als nächstes subtrahiert man auf beiden Seiten der Gleichung $40e^{x-1}$, damit auf der rechten Seite $0$ steht.

Zur 4. Zeile: Da der Faktor $e^{x+1}$ in beiden Summanden vorhanden ist, kann dieser ausgeklammert werden. Somit entsteht ein Produkt aus zwei Faktoren.

Zur 5. Zeile: Bei einem Produkt reeller Zahlen, das $0$ ergeben muss, kann der Satz vom Nullprodukt angewendet werden. Es werden im Folgenden also die beiden Faktoren einzelnen betrachtet.

Zur 6. Zeile: Der erste Faktor wird betrachtet: Dieser Faktor liefert keine Lösung der Gleichung, da der Term $e^{x-1}$ nie $0$ werden kann. 
Warum kann $e^{x-1}$ nicht $0$ werden? Laut der Definition einer Potenz handelt es sich hierbei um ein Produkt, bei dem $x-1$-mal der Faktor $e$ multipliziert wird. Ein Produkt kann aber nur dann $0$ werden, wenn einer der Faktoren $0$ ist. Da bei uns der Faktor $e$ ist, kann das Produkt also nie $0$ werden. Das gilt im Übrigen auch für die meisten anderen Potenzterme, da eine Potenz mit der Basis $0$ eine ziemlich langweilige Angelegenheit wäre. Daher gibt es ja die oben diskutierten Einschränkungen für die Basis. 

Ab der 7. Zeile: Der zweite Faktor ergibt eine quadratische Gleichung: Wird auf beiden Seiten durch $2$ dividiert, liegt sie in Normalform vor. Das ist die Voraussetzungen zur Anwendung der p-q-Formel. Dann kann die Gleichung wie gewohnt gelöst werden.

Bemerkung: Wenn Sie auf die Idee kommen, gleich die erste Zeile mit dem Faktor $e^{-(x-1)}$ zu multiplizieren, ist das auch völlig in Ordnung, da dieser Faktor nicht $0$ sein kann (siehe Kommentar zur 6. Zeile). Auf der linken Seite kürzen sich dann dieser Faktor und der Nenner weg. Auf der rechten Seite ergibt sich $e^{x-1}\cdot e^{-(x-1)}= e^{x-1-x+1}=e^0=1$. Damit sind die Exponentialterme "verschwunden" und man kann gleich in Zeile 7 weiterrechnen.

Beispiel 3:
$\begin{array}{crclcl}&\mathbb{D} &=& \mathbb{R} \\\\\text{1. Zeile:} & 100^t-3 &=& -\dfrac{11}{2}\cdot 10^t & \vert & + \dfrac{11}{2}\cdot 10^t \\\text{2. Zeile:} & 10^{2t}+ \dfrac{11}{2}\cdot 10^t-3 &=& 0 \\\text{3. Zeile:} & \left(10^t\right)^2+ \dfrac{11}{2}\cdot 10^t-3 &=& 0\end{array}$

Substitution: $u=10^t$
$\begin{array}{crclcl}\text{4. Zeile:} & u^{2}+ \dfrac{11}{2} u-3 &=& 0 & \vert & \text{p-q-Formel} \\\text{5. Zeile:} & u_{1,2} &=& -\dfrac{11}{4}\pm\sqrt{\left(\dfrac{11}{4}\right)^2+3} \\\\\text{6. Zeile:} & u_{1,2} &=& -\dfrac{11}{4}\pm\sqrt{\dfrac{169}{16}} \\\\\text{7. Zeile:} & u_1 &=& -\dfrac{11}{4}+\dfrac{13}{4} = \dfrac{1}{2} \\\text{8. Zeile:} & u_2 &=& -\dfrac{11}{4}-\dfrac{13}{4} = -6\end{array}$

Rücksubstitution:
$\begin{array}{rrclcl}\text{9. Zeile:} & u_1 = 10^t &=& -6 &\vert& \lg() \\\\\text{10. Zeile:} & t_1 &=& \lg\left(-6\right) \\\\\text{11. Zeile:} & u_2 = 10^t &=& \dfrac{1}{2} &\vert& \lg() \\\text{12. Zeile:} & t_2 &=& \lg\left(\dfrac{1}{2}\right) \\\\& \mathbb{L} &=& \left\{\lg\left(\dfrac{1}{2}\right)\right\}\end{array}$

Zur 1. Zeile: In dieser Exponentialgleichung sind nur Terme enthalten, die "Varianten" des Terms $10^t$ sind. Daher hat die Gleichung die benötigte Struktur, um sie mithilfe der Substitution lösen zu können. Dafür formen wir $100^t$ zu $10^{2t}$ um, denn $100$ ist ja nichts anderes als $10^2$. Des Weiteren addieren wir auf beiden Seiten $\dfrac{11}{2}\cdot 10^t$.

Zur 2. Zeile: Nun wenden wir das 3. Potenzgesetz auf $10^{2t}$ an und formen den Term zu $\left(10^t\right)^2$ um.

Zur 3. Zeile: Um jetzt eine quadratische Gleichung zu erhalten, wird $10^t$ durch $u$ substituiert.

Zur 4. bis 8. Zeile: Die substituierte Gleichung wird nun mit der p-q-Formel gelöst.

Zur 9. Zeile: Nun werden die beiden zuvor ausgerechneten Zwischenlösungen rücksubstituiert: Es wird also $u_1$ genommen und mit dem Ursprungsterm, in diesem Fall $10^t$, gleichgesetzt. Um die Gleichung zu lösen, wird der dekadische Logarithmus benötigt.

Zur 10. Zeile: Dieser Schritt bringt uns im Normalfall zu unserer ersten Lösung $t_1$. Hier ist es allerdings so, dass $-6$ nicht im Definitionsbereich des dekadischen Logarithmus liegt und daher keine Lösung berechnet werden kann.

Zur 11. Zeile: Das gleiche Vorgehen nun für $u_2$: Nach dem Aufstellen der Gleichung zur Rücksubstitution wird wieder der dekadische Logarithmus benötigt.

Zur 12. Zeile: Hier erhalten wir direkt die Lösung für $t_2$, da $\dfrac{1}{2}$ als positive Zahl ein erlaubtes Argument für den Logarithmus ist.

Bemerkung: Substitution ist ein recht häufiges Lösungsverfahren bei Exponentialgleichungen. Man erreicht dadurch, dass zwischenzeitlich keine Exponentialterme in der Gleichung mehr enthalten sind und man es (in diesem Fall) "ganz gemütlich" mit einer quadratischen Gleichung zu tun hat. Es kann natürlich passieren, dass z. B. eine kubische oder eine biquadratische Gleichung entsteht, aber auch dafür haben wir schon Lösungswege kennengelernt.

Exponentialfunktionen

Für Exponentialfunktionen gibt es natürlich ebenfalls typische Beispiele, die wir anhand verschiedener Fälle betrachten wollen. Anders als bei den gebrochen rationalen und Wurzelfunktionen spielt es hier bei der Unterscheidung der Fälle keine Rolle, ob die Zahlenwerte im Funktionsterm gerade bzw. ungerade sind, sondern ob die (immer positive) Basis größer oder kleiner als $1$ sind.

Eine Bemerkung vorab: Der Begriff "Exponentialfunktion" hat mehrere Bedeutungen: Manchmal wird er als Oberbegriff für alle Funktionen, bei denen die Variable im Exponenten steht, verwendet. Teilweise meint man damit konkret die Funktion $f(x)=e^x$, wobei $e\approx 2{,}7182$ die eulersche Zahl ist. Die Basis $e$ hat nämlich angenehmere Eigenschaften als andere Basen, wie wir beispielsweise bei Ableitungen sehen werden. Wirklich schlimm ist diese Mehrdeutigkeit allerdings nicht: Mit der Basistransformation können wir (wenn nötig) jede andere Exponentialfunktion so umformen, dass sie $e$ als Basis hat.

1. Fall

Wir beginnen mit Funktionsbeispielen, die eine Basis größer als $1$ haben. Das passt insofern, dass die typischen Basen für Exponentialfunktionen $2$, $e$ und $10$ sind. Schauen wir uns diesen Funktionen nun grafisch an: 

• $f_1(x)=e^x$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_2(x)=2^x$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_3(x) =10^x$ mit $\mathbb{D}=\mathbb{R}$

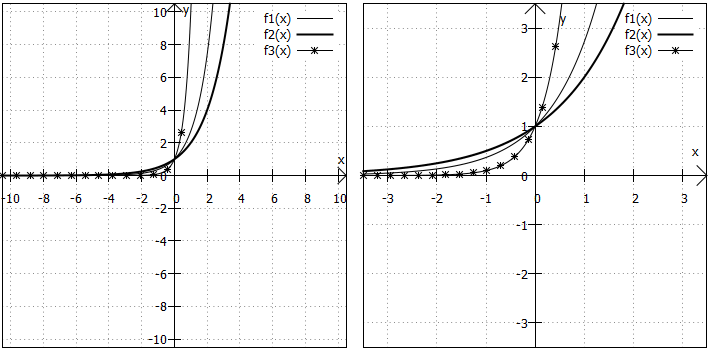
Wertebereich: Der Wertebereich dieser Exponentialfunktionen ist $\mathbb{D}=\mathbb{R}^+$. Wir hatten uns schon im Kapitel Potenzen, Wurzeln, Logarithmen überlegt, dass Potenzen mit positiver Basis immer positiv sein müssen. Da für Exponentialfunktionen laut Definition oben nur positive Basen (mit Ausnahme der $1$) infrage kommen, können die Funktionswerte folglich nie negativ oder $0$ werden.

Randverhalten: Für sehr kleine x-Werte nähert sich der Graph der $0$ an. Für sehr große x-Werte werden auch die Funktionswerte sehr groß. Exponentielles Wachstum ist dabei immer schneller als polynomiales Wachstum.

Symmetrie: Exponentialfunktionen sind nicht symmetrisch.

"Besondere Punkte": Exponentialfunktionen haben keine Nullstellen, Extrempunkte, Wende- und Polstellen.

Weitere Besonderheiten: 
Alle dieser einfachen Exponentialfunktionen verlaufen durch den Punkt $(0 \mid 1)$, denn $x^0 = 1$ für alle $x\in\mathbb{R}^+\setminus_{\{1\}}$.

Je größer die Basis im Funktionsterm ist, desto steiler verläuft der Graph im positiven x-Bereich und desto flacher verläuft der Graph im negativen x-Bereich.

2. Fall

Als Beispiele für Exponentialfunktionen mit einer Basis kleiner als $1$ betrachten wir die Kehrwerte der Funktionen aus dem 1. Fall:

• $f_4(x)=\dfrac{1}{e^x}=\left(\dfrac{1}{e}\right)^x$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_5(x)=\dfrac{1}{2^x}=\left(\dfrac{1}{2}\right)^x$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_6(x) =\dfrac{1}{10^x}=\left(\dfrac{1}{10}\right)^x$ mit $\mathbb{D}=\mathbb{R}$

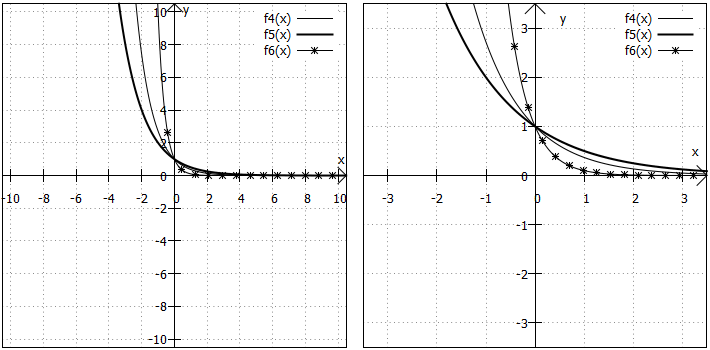
Wertebereich: Da die Basen bei diesen Funktionen zwar gebrochen, aber trotzdem positiv sind (sonst würden wir ja gegen die Definition der Exponentialfunktion verstoßen), bleibt es dabei: Der Wertebereich ist $\mathbb{D}=\mathbb{R}^+$.

Randverhalten: Bei Basen zwischen $0$ und $1$ verläuft die Funktion umgekehrt: Für sehr kleine x-Werte werden die Funktionswerte sehr groß und für sehr große x-Werte nähert sich der Graph der $0$ an.

Symmetrie: Auch in diesem Fall sind die Exponentialfunktionen nicht symmetrisch.

"Besondere Punkte": Exponentialfunktionen haben keine Nullstellen, Extrempunkte, Wende- und Polstellen.

Weitere Besonderheiten:
Wieder verlaufen alle Graphen durch den Punkt $(0 \mid 1)$.

Betrachtet man die Funktionen aus dem 1. und 2. Fall gemeinsam, fällt auf: Sind die Basen reziprok zueinander, sind die Graphen achsensymmetrisch zur y-Achse. Beispielsweise ist $f_1(x)$ mit der Basis $e$ spiegelbildlich zu $f_4(x)$ mit der Basis $\frac{1}{e}$ usw. Daraus folgt: Je größer die Basis, desto steiler der Graph - allerdings diesmal im negativen x-Bereich. Im positiven x-Bereich verlaufen Graphen von Funktionen mit großer Basis flacher.

3. Fall

Auch hier natürlich noch ein paar spannendere Beispielfunktionen:

• $f_7(x)=\dfrac{e^{(x+6)^2}}{15}$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_8(x)=5^{2x}-4\cdot 5^x$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_9(x)=e^{-x^2}$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_{10}(x)=e^x-e^{-x}$ mit $\mathbb{D}=\mathbb{R}$

Wertebereich: Der Wertebereich bei allgemeinen Exponentialfunktionen kann alle reellen Zahlen umfassen, siehe $f_{10}(x)$, oder einseitig unbeschränkt sein, was dem Normalfall bei Exponentialfunktionen entspricht. Bei $f_9(x)$ entspricht der Wertebereich dem halboffenen Intervall $]0; 1]$ und ist damit beidseitig beschränkt.

Randverhalten: Die Funktionen können sich an einer Seite des Definitionsbereichs einer festen Zahl annähern (z. B. $f_8(x)$), wie das für Exponentialfunktionen typisch ist. Bei $f_7(x)$ werden - aufgrund des quadratischen Exponenten - die Funktionswerte an beiden Rändern des Definitionsbereichs unbeschränkt groß. Die Kombination zweier Exponentialterme, von denen einer einen positiven und einer einen negativen Exponenten hat, führt dazu, dass die Funktionswerte bei $f_{10}(x)$ für große x-Werte sehr groß und für kleine x-Werte sehr klein werden.

Symmetrie: $f_7(x)$ ist achsensymmetrisch zu einer senkrechten Gerade durch $x=-6$. $f_9(x)$ ist achsensymmetrisch zur y-Achse. $f_{10}(x)$ ist punktsymmetrisch zum Koordinatenursprung. Die letzte Funktion folgt eher dem typischen Verlauf und ist daher nicht symmetrisch.

Weitere Besonderheiten:
Was Sie bei diesen Funktionen (mit Ausnahme von $f_9(x)$, wo der Exponentialterm im Nenner steht) sehen, ist ein ziemlich rasantes Wachstum. Das ist charakteristisch für Exponentialfunktionen.
Bitte beachten Sie, dass $f_9(x)=e^{-x^2} = \dfrac{1}{e^{x^2}}$ ist. Das ist nicht das gleiche wie $\dfrac{e}{x^2}$. Bei der alternativen Schreibweise für Potenzen mit negativen Exponenten muss die gesamte Potenz (dann mit positivem Exponenten) im Nenner stehen, nicht nur Teile davon. Basis und Exponent einer Potenz "verwandeln" sich nicht einfach so in Zähler und Nenner eines Bruches!