Dieses Kapitel enthält die folgenden Themen:

• Was ist eine Komplexe Zahl?
• Die gaußsche Zahlenebene 
• Darstellungsformen 
• Die eulersche Formel 
• Rechnen in C: Strichrechnung
• Rechnen in C: Punktrechnung 
• Rechnen in C: Potenzen 

25.2 Komplexe Zahlen - Erklärungen

Ein Hinweis vorab: In der Elektrotechnik und damit in vielen Ingenieurwissenschaften wird die imaginäre Einheit nicht mit $i$ sondern mit $j$ bezeichnet, weil dort $I$ und $i$ bereits für die Stromstärke vergeben sind. Bitte lassen Sie sich nicht davon irritieren, dass in diesem Text $i$ verwendet wird, wie es in der Mathematik üblich ist.

Warum komplexe Zahlen?

Vielfach taucht bei quadratischen Gleichungen und Polynomen die Begründung auf "... Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können ..." - natürlich kann man das! Um diese Einschränkung zu überwinden, haben Mathematiker nämlich die komplexen Zahlen "erfunden". Ganz wichtig zu nennen sind hierbei Carl Friedrich Gauß und Leonhard Euler. Die komplexen Zahlen haben sich in der Folge in vielen weiteren Bereichen und Zusammenhängen als sehr nützlich erwiesen, z. B. in der Elektrotechnik oder bei der Beschreibung von Schwingungen.
Die Bezeichnung "komplexe Zahlen" und damit ihr Symbol $\mathbb{C}$ leiten sich von dem lateinischen Wort "complexus" ab, welches "umfassend" bedeutet. Damit ist nicht gemeint, dass komplexe Zahlen besonders kompliziert wären ...

Die Eigenschaft, dass Wurzeln nun nicht mehr vor negativen Zahlen haltmachen, gipfelt in einem Satz, bei dem schon der Name auf seine Bedeutung hinweist, nämlich dem Fundamentalsatz der Algebra:
Es seien $n\in\mathbb{N}$ und $a_0, a_1,\dots , a_n\in\mathbb{C}$. Dann hat jedes Polynom $a_nx^n+a_{n-1}x^{n-1}+\dots +a_1x+a_0=0$ genau $n$ Lösungen $z_1, z_2,\dots ,z_n\in\mathbb{C}$ . Diese Lösungen müssen allerdings nicht alle verschieden sein.
Vielleicht erinnern Sie sich an den folgenden Satz im Kapitel Polynome: Die Anzahl der Nullstellen eines Polynoms ist im Bereich der reellen Zahlen maximal so groß wie der Grad des Polynoms. Dieses "maximal so groß" gibt zwar eine obere Grenze vor, lässt aber nach unten Spielraum. Diesen Spielraum gibt es im Bereich der komplexen Zahlen nicht mehr. Hier weiß man eindeutig: Ein Polynom vom Grade $3$ hat $3$ Nullstellen; ein Polynom vom Grad $17$ hat $17$ Nullstellen, vorausgesetzt man zählt die Häufigkeit dieser Nullstellen mit (man sagt mathematisch: ihre Vielfachheit). Und Eindeutigkeit ist etwas, was in der Mathematik ja bekanntermaßen sehr geschätzt wird ...

Was sind komplexe Zahlen?

Da es in dem Zahlenvorrat, den wir bislang kennen, kein Symbol gibt, mit dem man "Wurzel aus negativer Zahl" darstellen kann (sonst hätten wir es ja schon gefunden ...), musste man ein neues einführen. Es ist die imaginäre Einheit $i$ mit der Eigenschaft $i^2=-1$.

Betrachten wir eine quadratische Gleichung, die wir bislang nicht lösen konnten, z. B.:
$\begin{array}{rcl} x^2-4x+13 &=& 0 \cr &\dots & \cr x_{1,2} &=& 2\pm \sqrt{-9} \cr x_{1,2} &=& 2\pm \sqrt{9\cdot (-1)} \cr x_{1,2} &=& 2\pm 3\sqrt{-1} \cr x_{1,2} &=& 2\pm 3i \end{array}$

Komplexe Zahlen (man nennt sie üblicherweise $z$, manchmal auch $w$) lassen sich also schreiben als: $z=a+bi$ bzw. $z=(a,b)$ und die Menge der komplexen Zahlen als $\mathbb{C}=\{z \vert z=a+bi \,\text{mit}\; a,b\in\mathbb{R}\}$

Eine komplexe Zahl ist also ein geordnetes Paar reeller Zahlen. $a= \textit{Re}(z)$ nennt man den Realteil von $z$ und $b=\textit{Im}(z)$ den Imaginärteil von $z$. Ist $\textit{Im}(z)=0$, so erhalten wir eine reelle Zahl. Die reellen Zahlen sind also in den komplexen enthalten. Ist $\textit{Re}(z)=0$ , so nennen wir die Zahl rein imaginär.
Bemerkung: Sowohl Real- als auch Imaginärteil sind reelle Zahlen! Die imaginäre Einheit $i$ "gehört" also nicht zum Imaginärteil selbst dazu.

Ein Beispiel: $\sqrt{-4}=\sqrt{4\cdot (-1)}=\sqrt{4}\cdot\sqrt{-1}=2i=0+2i$
Der Realteil ist hier $0$ und der Imaginärteil $2$.

Ein einfacher Satz zu komplexen Zahlen: Zwei komplexe Zahlen sind dann gleich, wenn ihre Realteile und ihre Imaginärteile gleich sind.

Darstellung in der gaußschen Zahlenebene

Von den reellen Zahlen sind wir die Darstellung auf dem Zahlenstrahl gewöhnt. Für komplexe Zahlen ist dort aber "kein Platz" mehr, da die reellen Zahlen den Zahlenstrahl bereits vollständig ausfüllen. Die naheliegende Lösung ist, statt eines Zahlenstrahls ein Koordinatensystem zu verwenden - naheliegend deshalb, weil wir auch schon früher Paare reeller Zahlen in ein Koordinatensystem eingetragen haben, nämlich bei Punkten. In Abgrenzung zu Funktionen und Graphen nennt man dieses Koordinatensystem komplexe Ebene oder (vielleicht sogar noch üblicher) gaußsche Zahlenebene. Die Achsen heißen hier nicht x-Achse und y-Achse, sondern reelle Achse (horizontal - hier finden wir, wie wir das vom Zahlenstrahl gewöhnt sind, die reellen Zahlen) und imaginäre Achse (senkrecht - auf dieser Achse befinden sich die rein imaginären Zahlen).

Ein paar Beispiele:
$z_1=4+3i$
$z_2=-7+6i$
$z_3=-3-5i$
$z_4=2-8i$

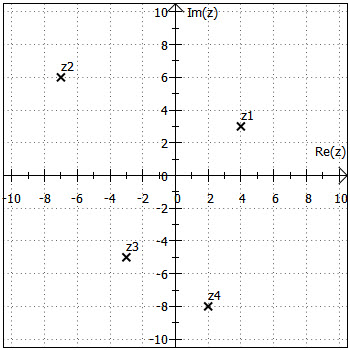
Das Ziel, das grundsätzlich bei jeder Zahlenbereichserweiterung verfolgt wird, ist, dass alle bisherigen Rechenregeln und -gesetze erhalten bleiben, dass sich also die "neuen" Zahlen möglichst gut in das Gewohnte und Bewährte einpassen, sonst müsste man ja jeweils alles neu "erfinden", auch Zusammenhänge, die sich bereits bewährt haben. Oder man würde für jeden Zahlenbereich eigene Rechengesetze erhalten, was ja nun auch unpraktisch wäre, z. B. addiert man natürliche und rationale Zahlen auf gleiche Weise. Dass man bei rationalen Zahlen ggf. vor der Addition erweitern muss und bei natürlichen Zahlen nicht, liegt ja nur daran, dass natürliche Zahlen definitionsgemäß den gleichen "Nenner" haben, nämlich $1$. Fast noch wichtiger als einzelne Rechentechniken sind die grundlegenden Rechengesetze, insbesondere Assoziativ-, Kommutativ- und Distributivgesetz, die natürlich auch für komplexe Zahlen gelten.
Bei den komplexen Zahlen ist dies weitgehend gelungen, mit einer Ausnahme: Die Anordnung geht verloren. Anders als auf dem Zahlenstrahl, wo bei zwei Zahlen $x$ und $y$ immer entschieden werden kann, ob $x$ größer ist als $y$, ob $x$ und $y$ gleich sind oder ob $x$ kleiner ist als $y$, geht dies bei komplexen Zahlen nicht, wie bei Darstellung in der gaußschen Zahlenebene deutlich wird. Nach welchen Kriterien sollte beispielsweise entschieden werden, ob $z_1$ oder $z_2$ aus der Grafik oben "größer" ist? Aus diesem Grund gibt es auch keine positiven und negativen komplexen Zahlen, denn die Konzepte "positiv" und "negativ" geben ja Auskunft über die Lage einer Zahl bezogen auf die $0$.

Darstellungsformen

Es gibt verschiedene Darstellungsmöglichkeiten komplexer Zahlen. Sie haben insofern alle eine Berechtigung, da in den einzelnen Darstellungsformen jeweils andere Rechenoperationen und mathematische Zusammenhänge gut durchzuführen bzw. zu erklären sind.

Kartesische Form

Wie oben schon eingeführt, können komplexe Zahlen in der Form
$z=a+bi$ oder $z=(a,b)$ mit $a,b \in \mathbb{R}$
dargestellt werden. Dies nennt man auch Komponenten- oder algebraische Form.

Trigonometrische Form

Alternativ zur Festlegung über $a=\textit{Re}(z)$ und $b=\textit{Im}(z)$ ist eine komplexe Zahl auch dann eindeutig bestimmt, wenn man ihren Abstand vom Ursprung, Betrag genannt, $\vert z \vert=r$ und den zugehörigen Winkel $\varphi$ kennt. $\varphi$ ist der griechische Buchstabe "phi" und wird gerne für die Winkel komplexer Zahlen verwendet. Diese Schreibweise nennt man auch Polarkoordinaten. Für zwei Beispielzahlen sind ihre Polarkoordinaten in der linken Grafik dargestellt. Die "Linie" bzw. der "Pfeil" vom Ursprung hin zu der komplexen Zahl wird dabei auch Zeiger, der Winkel einer komplexen Zahl Argument oder Phase genannt.

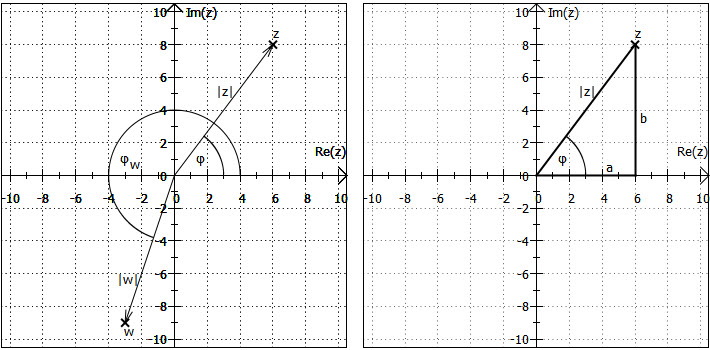
Berechnung: Wie die rechte Grafik zeigt, gilt:
für den Betrag (über den Satz des Pythagoras): $r=\vert z \vert=\sqrt{a^2+b^2}$
für das Argument (mit ein bisschen Trigonometrie): $\varphi=\arctan\left(\dfrac{b}{a}\right)$

Bemerkung: Bitte beachten Sie, dass die Berechnung des Arguments in dieser Form nur funktioniert, wenn sich die komplexe Zahl im ersten Quadranten befindet. Liegt $z$ im zweiten Quadranten (siehe Beispiel 2 etwas weiter unten), kann man ausnutzen, dass es auch hier ein Dreieck gibt, das Katheten mit den Längen $a$ und $b$ hat. Der hieraus berechnete Winkel $\varphi '$ beschreibt aber nicht das gesuchte Argument, da es zwischen dem Zeiger und der negativen x-Achse liegt. Da sich $\varphi '$ und $\varphi$ aber gerade zu $180^\circ$ bzw. $\pi$ ergänzen, hilft einfaches Subtrahieren weiter. Nach dieser Methode muss bei komplexen Zahlen im dritten Quadranten $180^\circ$ bzw. $\pi$ zu $\varphi '$ addiert werden und im vierten Quadranten $\varphi '$ von $360^\circ$ bzw. $2\pi$ subtrahiert werden. Liegt eine komplexe Zahl direkt auf einer der Achsen, muss ohnehin nicht weiter gerechnet werden, weil diese Winkel bekannt sind. Für diese Rechnung ist es also nötig, sich vorab Klarheit darüber zu verschaffen, mit welchem Quadranten man es zu tun hat. Eine kleine Skizze wirkt hier - wie immer - Wunder ...


Wie sieht die trigonometrische Form nun also aus?
Vorausgesetzt $r\neq0$ lässt sich jede komplexe Zahl schreiben als: $z=r(\cos(\varphi)+i\sin(\varphi))$, wobei $\varphi \; \in \; [0 \, ; \, 2\pi[$

Bemerkung: Wenn der Betrag $r$ einer komplexen Zahl $0$ ist, liegt diese Zahl im Ursprung. Dann braucht man auch kein Argument ...

Aus der rechten Grafik oben kann man ableiten, dass $a=r\cos(\varphi)$ und $b=r\sin(\varphi)$ gilt (Wer damit Schwierigkeiten hat, sollte sich noch mal das Trigonometrie-Kapitel anschauen.). Setzt man diese Beziehungen in die allererste Definition komplexer Zahlen ein, erhält man ohne viel zu rechnen die trigonometrische Darstellungsform:
$z=a+bi=r\cos(\varphi)+r\sin(\varphi) \cdot i=r(\cos(\varphi)+i\sin(\varphi))$
Damit haben wir diese Form auch schon hergeleitet.


Warum wird das Argument von $z$ auf das Intervall $[0 \, ; \, 2\pi[$ eingeschränkt?
Hier kommt wieder die Eindeutigkeit ins Spiel: Würde man ein größeres Intervall zulassen, wäre die Darstellung in Polarkoordinaten mehrdeutig - weitere komplexe Zahlen würden hingegen nicht entstehen. Betrachten wir beispielsweise das Argument $\varphi=\dfrac{\pi}{3}$. Bezüglich der Position seines Zeigers unterscheidet es sich nicht von $\dfrac{7\pi}{3}=2\pi+\dfrac{\pi}{3}$ (etwas unmathematisch formuliert: erst einmal im Kreis rum und dann noch $\dfrac{\pi}{3}$ dazu) und auch nicht von $\dfrac{13\pi}{3}=4\pi+\dfrac{\pi}{3}$ (entsprechend: zweimal im Kreis rum und dann noch $\dfrac{\pi}{3}$) etc. Allgemein gesagt: $\varphi=2k\pi+\dfrac{\pi}{3}$ ($k\in\mathbb{Z}$, also k-mal im Kreis rum und dann noch $\dfrac{\pi}{3}$) liefert die gleiche Position des Zeigers wie $\varphi=\dfrac{\pi}{3}$. Daher werden beim Argument einer komplexen Zahl Vielfache von $2\pi$ außer Acht gelassen, weil dies keine wirkliche Einschränkung ist. Manchmal werden auch andere Intervalle gewählt, z. B. $[-\pi \, ; \, \pi[$ . Letztendlich macht das keinen Unterschied. Hauptsache, ein kompletter Kreis ist abgedeckt; sonst würde man in der Tat komplexe Zahlen "verlieren".


Beispiel 1:
Gegeben sei die komplexe Zahl $z=2+2i$
Ihr Betrag ergibt sich zu: $r=\sqrt{2^2+2^2}=\sqrt{8}$
Ihr Argument ist: $\varphi=\arctan\left(\dfrac{2}{2}\right)=\dfrac{\pi}{4}$
In trigonometrischer Darstellung ist also $z=\sqrt{8}\left(\cos\left(\dfrac{\pi}{4}\right)+i\sin\left(\dfrac{\pi}{4}\right)\right)$
Bemerkung: Bei diesen Umrechnungen ist es immer sinnvoll, nicht den Sinus oder Kosinus für die Bestimmung des Arguments zu verwenden, weil dann die Hypotenuse, sprich der Betrag der komplexen Zahl benötigt würde. Diesen müssen wir zwar sowieso auch berechnen, allerdings entstehen hier in den meisten Fällen Rundungsfehler, die man vermeidet, wenn man Tangens bzw. Arkustangens verwendet.

Beispiel 2:
Gegeben sei nun die komplexe Zahl $z=-7+6i$
Ihr Betrag ergibt sich zu: $r=\sqrt{7^2+6^2}=\sqrt{85}$
Ihr Argument ist: $\varphi=180^\circ-\arctan\left(\dfrac{6}{7}\right)\approx 139{,}40^\circ$
In trigonometrischer Darstellung ist also $z\approx\sqrt{85}\left(\cos\left(139{,}40^\circ\right)+i\sin\left(139{,}40^\circ\right)\right)$
Bemerkung 1: Da das Vorzeichen von $-7$ nach dem Quadrieren sowieso keine Rolle mehr spielen würde, wurde es hier gleich weggelassen. Außerdem ist die Länge von Katheten ohnehin positiv.
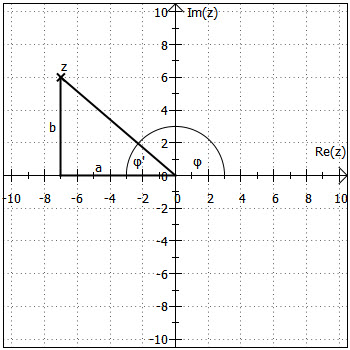
Bemerkung 2: Der über den Arkustangens berechnete Winkel liegt in dem rechtwinkligen Dreieck mit den Katheten $a$ und $b$. In der Grafik unten wurde er mit $\varphi'$ bezeichnet. Das ist nur leider (wie oben schon erläutert) nicht das gesuchte Argument $\varphi$, welches ja zwischen der positiven x-Achse und dem Zeiger liegen muss. Die Summe von $\varphi$ und $\varphi'$ ergibt aber genau $180^\circ$ , sodass es letztendlich reicht, $\varphi'$ zu kennen, um $\varphi$ zu bestimmen.

Exponentialform

Über die eulersche Formel oder auch eulersche Relation $e^{i\varphi}=\cos(\varphi)+i\sin(\varphi)$ gelangt man zur nächsten Darstellungsform, nämlich:
$z=re^{i\varphi}$
mit dem Betrag $r$ und dem Argument $\varphi$, wobei $\varphi \; \in \; [0 \, ; \, 2\pi[$

Umrechnung: Ist die komplexe Zahl in kartesischer Form gegeben, müssen Betrag und Argument berechnet werden. Das wurde oben gerade beschrieben. Wenn die komplexe Zahl in trigonometrischer Form vorliegt, ist nichts weiter zu berechnen.

Beispiel:
Gegeben sei immer noch $z=2+2i$
In Exponentialform sieht diese Zahl dann so aus: $z=\sqrt{8}e^{i \, \frac{\pi}{4}}$


Ganz wichtiger Satz: Die so genannte eulersche Identität: $e^{i\pi}+1=0$
Wenn man die oben genannte eulersche Formel anwendet, ergibt sich dieser Zusammenhang ganz einfach, wenn man betrachtet, was für $\varphi = \pi$ passiert:
$e^{i\pi}=\cos(\pi)+i\sin(\pi)$
Nun ist aber (ganz unabhängig von den komplexen Zahlen) $\cos(\pi)=-1$ und $\sin(\pi) =0$
Fügt man das alles in der Formel zusammen, erhält man $e^{i\pi}=-1+i\cdot 0$ , also $e^{i\pi}+1= 0$

In dieser Formel werden fünf wichtige (die fünf wichtigsten?) mathematische Konstanten in Beziehung zueinander gesetzt, nämlich $0$, $1$, $e$, $\pi$ und $i$. Das ist wirklich nicht wenig! Manche Mathematiker und Mathematikerinnen halten diese Formel für so bestaunenswert wie die Mona Lisa.
Eine Bemerkung am Rande: Die eulersche Identität wurde vor einer Weile in der Zeitschrift "The Mathematical Intelligencer" zum schönsten mathematischen Satz gewählt. Bei der Abstimmung, bei der es explizit um Schönheit und nicht um Anwendungsmöglichkeiten oder die Bedeutung der Sätze ging, setzte sich die eulersche Identität durch u. a. gegen "Es gibt unendlich viele Primzahlen.", "Es gibt keine rationale Zahl, deren Quadrat $2$ ist." und "Jede ebene Landkarte kann mit vier Farben so gefärbt werden, dass aneinandergrenzende Länder nicht gleich gefärbt sind." [vergleiche: Beutelspacher, Albrecht (2001): "In Mathe war ich immer schlecht". Braunschweig/Wiesbaden, S. 49f]

Wie rechnet man mit komplexen Zahlen?

Im diesem Abschnitt schauen wir uns u. a. an, wie die Grundrechenarten mit komplexen Zahlen funktionieren.

Eine Bemerkung vorab: Wir hatten oben schon gesehen, dass für die imaginäre Einheit $i$ manche Sachen anders sind, als wir es aus früheren Kapiteln kennen. Beispielsweise können wir nun mit Zahlen umgehen, deren Quadrat negativ ist. Ganz wichtig ist aber, dass die üblichen Rechenregeln und -gesetze weiterhin ganz normal gelten. Das betrifft neben den Rechengesetzen und den Regeln der Bruch- und Potenzrechnung beispielsweise auch das Gesetz Potenz- vor Punkt- vor Strichrechnung! Lassen Sie sich also nicht davon irritieren, dass $i$ "irgendwie ungewohnt" ist ... Es wäre aus mathematischer Sicht überhaupt nicht sinnvoll, an den bestehenden, bekannten und bewährten Rechenoperationen etwas zu ändern!

Addition und Subtraktion

Komplexe Zahlen kann man nur in der kartesischen Form addieren und subtrahieren. Man addiert / subtrahiert komplexe Zahlen, in dem man die Realteile addiert / subtrahiert und die Imaginärteile addiert / subtrahiert. Um diese Rechenverfahren zu durchschauen, braucht es (hoffentlich) keine Formeln, sondern nur ein paar Beispiele:

Beispiele:
Wir nehmen die komplexen Zahlen $z_1=3+5i$ und $z_2=-2+8i$.

Summe:
$\begin{array}{rcl}z_1+z_2 &=& (3+5i)+(-2+8i) \\ &=& 3-2+5i+8i \\ &=& 1+13i\end{array}$

Differenz:
$\begin{array}{rcl}z_1-z_2 &=& (3+5i)-(-2+8i) \\ &=& 3+2+5i-8i \\ &=& 5-3i\end{array}$

Bemerkung: Einzig die Klammern um $z_2$ bei der Bildung der Differenz waren bei diesen zwei Rechnungen wirklich nötig. Alle anderen hätten auch weggelassen werden können.
Wichtig: Wie immer ändert das Minuszeichen vor der Klammer alle Vor- und Rechenzeichen in der Klammer.

Multiplikation und Division

Multiplizieren und dividieren kann man komplexe Zahlen in allen hier vorgestellten Schreibweisen. Dass auch bei den komplexen Zahlen nicht durch $0$ geteilt werden darf, versteht sich dabei von selbst.

Für die Division benötigen wir gleich ein spezielles Konzept, welches es bei reellen Zahlen noch nicht gab.
Definition: Zu einer komplexen Zahl $z=a+bi$ heißt $\bar{z}=a-bi$ die konjugiert komplexe Zahl.
In der gaußschen Zahlenebene erhält man die konjugiert komplexe einer Zahl $z$, indem man $z$ an der reellen Achse spiegelt.

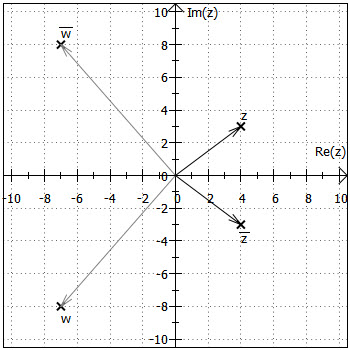
Bemerkung: In der Grafik sind zwei komplexe Zahlen mit ihren konjugiert Komplexen sowie alle zugehörigen Zeiger eingezeichnet.

Es gilt: $\vert z \vert^2=z\cdot \bar{z}$
Das Produkt einer komplexen Zahl mit ihrer konjugiert komplexen ist also ihr Betrag "zum Quadrat" und dieses ist immer reell (kann man einfach nachrechnen). Es entstehen ja keine Summanden, die ein einzelnes $i$ enthalten (3. binomische Formel ...) und das $i^2$ wird (sollte ja inzwischen nicht mehr überraschen ...) zu $-1$.


Multiplikation und Division in kartesischer Form
Für die kartesische Form gibt es wieder "nur" ein paar Beispiele mit Erläuterungen für die Multiplikation und Division:

Beispiele:
Wir nehmen wieder $z_1=3+5i$ und $z_2=-2+8i$.

Produkt:
$\begin{array}{rcl}z_1 \cdot z_2 &=& (3+5i)\cdot(-2+8i) \\ &=& 3\cdot(-2)+3\cdot 8i-5i\cdot 2+5\cdot 8i^2 \\ &=& -6+24i-10i-40 \\ &=& -46+14i\end{array}$
Die Klammern werden ausmultipliziert. Bei der vorletzten Umformung wird benutzt, dass $i^2=-1$ ist, daher ist $5 \cdot 8i^2 = 5\cdot 8 \cdot (-1)=-40$.

Quotient:
$\begin{array}{rcl}\dfrac{z_1}{z_2} &=& \dfrac{3+5i}{-2+8i} \\ \\ &=& \dfrac{(3+5i)(-2-8i)}{(-2+8i)(-2-8i)} \\ \\ &=& \dfrac{-6-24i-10i+40}{4-64i^2} \\ \\ &=& \dfrac{34-34i}{4+64} \\ \\ &=& \dfrac{34}{68}-\dfrac{34i}{68} \\ \\ &=& \dfrac{1}{2}-\dfrac{1}{2}i\end{array}$
Hier ist ein bisschen mehr zu erklären, insbesondere bei der ersten Umformung: Bislang wurde ja nicht definiert, wie man durch das $i$ teilt - und das ist auch gar nicht nötig. Wir stellen uns stattdessen folgende Frage: Mit welchem Term muss der Bruch erweitert werden, damit das $i$ im Nenner "verschwindet"? Hier kommt die gerade definierte konjugiert komplexe Zahl von $z_2$ ins Spiel. Multipliziert man nämlich eine komplexe Zahl mit ihrer konjugiert Komplexen ist das Ergebnis immer reell (siehe oben). Es darf natürlich nicht vergessen werden, dass auch der Zähler mit der konjugiert Komplexen von $z_2$ multipliziert werden muss, sonst wäre es ja kein Erweitern. Anschließend wird ausmultipliziert und zusammengefasst. Zum Abschluss kann die komplexe Zahl im Zähler dann komponentenweise durch den reellen Nenner geteilt werden.
Bemerkung: Ganz ähnlich ist der Rechenweg bei Wurzeltermen, wenn dort Wurzeln im Nenner stehen (siehe z. B. Aufgabe 5.16 im Kapitel Potenzen, Wurzeln, Logarithmen).
Wichtig: Auch beim Rechnen mit komplexen Zahlen darf man natürlich nicht aus Summen kürzen!


Multiplikation und Division in trigonometrischer und exponentieller Form
Bei Multiplikation und Division kommt eine der Stärken der trigonometrischen und exponentiellen Schreibweisen zum Tragen. Es gilt nämlich für $z_1=r_1e^{i\varphi_1}$ und $z_2=r_2e^{i\varphi_2}$:

Multiplikation: $z_1\cdot z_2=r_1e^{i\varphi_1} \cdot r_2e^{i\varphi_2} = r_1r_2e^{i\varphi_1+i\varphi_2} = r_1r_2e^{i(\varphi_1+\varphi_2)}$
Bemerkung: Verwendet wurden einfach die Regeln für die Multiplikation von Potenzen. Es werden also die Beträge multipliziert und die Argumente addiert.

Division: $\dfrac{z_1}{z_2}=\dfrac{r_1e^{i\varphi_1}}{r_2e^{i\varphi_2}}=\dfrac{r_1}{r_2}e^{i\varphi_1-i\varphi_2}=\dfrac{r_1}{r_2}e^{i(\varphi_1-\varphi_2)}$
Bemerkung: Nach den Regeln der Potenzrechnung wird vermutlich nicht verwundern, dass hier nun die Beträge dividiert und die Argumente subtrahiert werden.

Wichtig: Natürlich gilt auch hier Potenz- geht vor Punkt- geht vor Strichrechnung.

Da Betrag und Argument der exponentiellen Schreibweise die gleichen sind wie bei der trigonometrischen, gilt also hier für $z_1=r_1\left(\cos(\varphi_1)+i \sin(\varphi_1)\right)$ und $z_2=r_2\left(\cos(\varphi_2)+i \sin(\varphi_2)\right)$:

$z_1\cdot z_2=r_1r_2\left(\cos(\varphi_1+\varphi_2)+i \sin(\varphi_1+\varphi_2)\right)$ beziehungsweise

$\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}\left(\cos(\varphi_1-\varphi_2)+i \sin(\varphi_1-\varphi_2)\right)$


Beispiele:
Wir nehmen die komplexen Zahlen $z_1=\dfrac{1}{2}e^{i\,\frac{5\pi}{4}}$ und $z_2=10e^{i\,\frac{\pi}{6}}$.

Produkt: 
$\begin{array}{rcl}z_1 \cdot z_2 &=& \dfrac{1}{2}e^{i\,\frac{5\pi}{4}}\cdot 10e^{i\,\frac{\pi}{6}} \\ \\ &=& \dfrac{1}{2}\cdot 10e^{i\,\frac{5\pi}{4}+i\,\frac{\pi}{6}} \\ \\ &=& 5e^{i\,\frac{17\pi}{12}}\end{array}$

Quotient:
$\begin{array}{rcl}\dfrac{z_1}{z_2} &=& \dfrac{\frac{1}{2}e^{i\,\frac{5\pi}{4}}}{10e^{i\,\frac{\pi}{6}}} \\ \\ &=& \dfrac{\frac{1}{2}}{10}e^{i\,\frac{5\pi}{4}-i\,\frac{\pi}{6}} \\ \\ &=& \dfrac{1}{20}e^{i\,\frac{13\pi}{12}}\end{array}$


Wir nehmen nun $z_1=3\left(\cos\left(\dfrac{\pi}{3}\right)+i\sin\left(\dfrac{\pi}{3}\right)\right)$ und $z_2=\dfrac{1}{4}\left(\cos\left(\dfrac{5\pi}{9}\right)+i\sin\left(\dfrac{5\pi}{9}\right)\right)$.

Produkt:
$\begin{array}{rcl}z_1\cdot z_2 &=& 3\left(\cos\left(\dfrac{\pi}{3}\right)+i\sin\left(\dfrac{\pi}{3}\right)\right)\cdot\dfrac{1}{4}\left(\cos\left(\dfrac{5\pi}{9}\right)+i\sin\left(\dfrac{5\pi}{9}\right)\right) \\ \\ &=& 3\cdot \dfrac{1}{4}\left(\cos\left(\dfrac{\pi}{3}+\dfrac{5\pi}{9}\right)+i\sin\left(\dfrac{\pi}{3}+\dfrac{5\pi}{9}\right)\right) \\ \\ &=& \dfrac{3}{4}\left(\cos\left(\dfrac{8\pi}{9}\right)+i\sin\left(\dfrac{8\pi}{9}\right)\right)\end{array}$

Quotient:
$\begin{array}{rcl}\dfrac{z_1}{z_2} &=&\dfrac{3\left(\cos\left(\dfrac{\pi}{3}\right)+i\sin\left(\dfrac{\pi}{3}\right)\right)}{\frac{1}{4}\left(\cos\left(\dfrac{5\pi}{9}\right)+i\sin\left(\dfrac{5\pi}{9}\right)\right)} \\ \\ &=& \dfrac{3}{\frac{1}{4}}\left(\cos\left(\dfrac{\pi}{3}-\dfrac{5\pi}{9}\right)+i\sin\left(\dfrac{\pi}{3}-\dfrac{5\pi}{9}\right)\right) \\ \\ &=&12\left(\cos\left(\dfrac{-2\pi}{9}\right)+i\sin\left(\dfrac{-2\pi}{9}\right)\right) \\ \\ &=& 12\left(\cos\left(\dfrac{16\pi}{9}\right)+i\sin\left(\dfrac{16\pi}{9}\right)\right)\end{array}$
Bemerkung: Die letzte Umformung bewirkt, dass das Argument, wie oben "gefordert", im Intervall $[0;2\pi[$ liegt. Dazu wurde zu dem Argument $\frac{-2\pi}{9}$ einfach $2\pi$ addiert.


In kartesischer Form ist von den vier Grundrechenarten also nur die Division ein bisschen tricky. Bei Addition, Subtraktion und Multiplikation kann man eigentlich genauso rechnen, wie man es intuitiv tun würde und muss sich nur bei der Multiplikation gelegentlich daran erinnern, dass $i^2=-1$ ist. Multiplikation und Division von komplexen Zahlen in trigonometrischer bzw. exponentieller Form erfolgt zwar anders, als man wohl vorab vermutet hätte, ist dafür aber sehr einfach.

Potenzen und Wurzeln

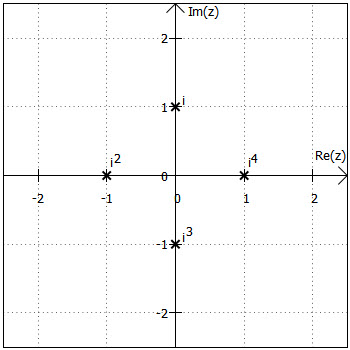
Zunächst ist wichtig, sich die Potenzen von $i$ zu verdeutlichen. Es gilt:
$i^1=i=\sqrt{-1}$
$i^2=i\cdot i=-1$
$i^3=i\cdot i\cdot i=-i$
$i^4=i\cdot i\cdot i\cdot i=1$
$i^5=i\cdot i\cdot i\cdot i\cdot i=\sqrt{-1}$
$i^6=i\cdot i\cdot i\cdot i\cdot i\cdot i=-1$
...
Mehr passiert nicht. Kann auch gar nicht ...

Das Potenzieren komplexer Zahlen ist grundsätzlich auch in allen vorgestellten Schreibweisen möglich. Üblicherweise möchte man aber komplexe Zahlen in kartesischer Schreibweise nicht potenzieren, weil es unglaublich viel komplizierter als in trigonometrischer oder exponentieller Darstellung ist. Es lohnt sich selbst dann noch, wenn man erst umrechnen muss ...


Ähnlich wie beim Multiplizieren und Dividieren gibt es auch hier eine Formel, mit deren Hilfe sich das Potenzieren komplexer Zahlen auf sehr einfache, reelle Rechenoperationen zurückführen lässt. Es gilt für $z=re^{i\varphi}$ und $n\in\mathbb{N}$:
$z^n=\underbrace{re^{i\varphi} \cdot re^{i\varphi} \cdot \ldots \cdot re^{i\varphi}}_n=r\cdot r\cdot \ldots \cdot re^{i\varphi +i\varphi + \ldots +i\varphi}=r^ne^{i n\varphi}$

bzw. für $z=r\left(\cos\left(\varphi\right)+i\sin\left(\varphi\right)\right)$ und $n\in\mathbb{N}$:
$z^n=r^n\left(\cos\left(n\varphi\right)+i\sin\left(n\varphi\right)\right)$

Bemerkung 1: Dieser wichtige Zusammenhang heißt Satz von de Moivre nach dem französischen Mathematiker Abraham de Moivre.
Bemerkung 2: Hier erhält man über die Anwendung der Potenzgesetze eine Rechenvorschrift, in der nur noch der Betrag entsprechend potenziert und das Argument mit dem Exponenten multipliziert werden muss. Überlegen Sie sich jetzt, was man tun müsste, um eine komplexe Zahl in kartesischer Darstellung zu potenzieren. Zu berechnen wäre: $(a+bi)(a+bi)\ldots(a+bi)$. Kann man machen, muss man aber nicht ...

Beispiele:
Bei den komplexen Zahlen $z_1=\dfrac{1}{2}e^{i\,\frac{5\pi}{4}}$ und $z_2=\dfrac{1}{4}\left(\cos\left(\dfrac{5\pi}{9}\right)+i\sin\left(\dfrac{5\pi}{9}\right)\right)$ von oben berechnet man:
$\begin{array}{rcl}z_1^4 &=& \left(\dfrac{1}{2}\right)^4e^{i\,\cdot 4\cdot\frac{5\pi}{4}} \\ \\ &=& \dfrac{1}{16} e^{i\,\cdot 5\pi} \\ \\ &=& \dfrac{1}{16} e^{i\,\pi} \\ \\ &=& -\dfrac{1}{16}\end{array}$


$\begin{array}{rcl}z_2^{12} &=& \left(\dfrac{1}{4}\right)^{12}\left(\cos\left(12\cdot\dfrac{5\pi}{9}\right)+i\sin\left(12\cdot\dfrac{5\pi}{9}\right)\right) \\ \\ &=& \dfrac{1}{16.777.216}\left(\cos\left(\dfrac{20\pi}{3}\right)+i\sin\left(\dfrac{20\pi}{3}\right)\right) \\ \\ &=& \dfrac{1}{16.777.216}\left(\cos\left(\dfrac{2\pi}{3}\right)+i\sin\left(\dfrac{2\pi}{3}\right)\right)\end{array}$


Als letzte Rechenoperation betrachten wir das Radizieren, also das Ziehen von Wurzeln:
Naheliegend, wenn man vom Satz von de Moivre ausgeht, ist der Gedanke, dass sich die $n$-te Wurzel ($n\in\mathbb{N}$) einer komplexen Zahl nach der folgenden Formel berechnen lässt: $\sqrt[n]{z}=\sqrt[n]{r}\left(\cos\left(\dfrac{\varphi}{n}\right)+i\sin\left(\dfrac{\varphi}{n}\right)\right)$
Das ist nicht grundsätzlich falsch, aber auch nicht vollständig richtig. Hierbei wird nämlich außer Acht gelassen, dass Sinus und Kosinus ja nun periodische Funktionen sind mit der Periode $2\pi$. Ersetzt man $\varphi$ durch $\varphi+2k\pi$ mit $k\in\mathbb{Z}$ (addiert man also zum Argument ein Vielfaches von $2\pi$), erhält man das gleiche $z$, aber z. T. unterschiedliche Wurzelwerte. Der Wurzelterm in $\mathbb{C}$ ist also mehrdeutig (im Unterschied zu Wurzeln im Bereich der reellen Zahlen). Man erhält die Formeln:

$\sqrt[n]{z}=\sqrt[n]{r}e^{i \, \frac{\varphi+2k\pi}{n}}$ bzw. $\sqrt[n]{z}=\sqrt[n]{r}\left(\cos\left(\dfrac{\varphi+2k\pi}{n}\right)+i\sin\left(\dfrac{\varphi+2k\pi}{n}\right)\right)$
mit $k=0,1,...,n-1$


Für die restlichen wichtigen Eigenschaften, ein Beispiel:
Wir nehmen die komplexe Zahl $z=8=8\left(\cos\left(0\right)+i\sin\left(0\right)\right)$.
Gesucht sind alle dritten Wurzeln von $z$.

$k=0$:
$\begin{array}{rcl}z_0 &=& \sqrt[3]{8}\left(\cos\left(\dfrac{0+2\cdot 0\cdot\pi}{3}\right)+i\sin\left(\dfrac{0+2\cdot 0\cdot\pi}{3}\right)\right) \\ &=& 2\left(\cos\left(0\right)+i\sin\left(0\right)\right) \\ &=& 2\end{array}$
Diese Wurzel kennen wir schon ...

$k=1$:
$\begin{array}{rcl}z_1 &=& \sqrt[3]{8}\left(\cos\left(\dfrac{0+2\cdot 1\cdot\pi}{3}\right)+i\sin\left(\dfrac{0+2\cdot 1\cdot\pi}{3}\right)\right) \\ \\ &=& 2\left(\cos\left(\dfrac{2\pi}{3}\right)+i\sin\left(\dfrac{2\pi}{3}\right)\right)\end{array}$

$k=2$:
$\begin{array}{rcl}z_2 &=& \sqrt[3]{8}\left(\cos\left(\dfrac{0+2\cdot 2\cdot\pi}{3}\right)+i\sin\left(\dfrac{0+2\cdot 2\cdot\pi}{3}\right)\right) \\ \\ &=&2\left(\cos\left(\dfrac{4\pi}{3}\right)+i\sin\left(\dfrac{4\pi}{3}\right)\right)\end{array}$

Wie bei allen Wurzelrechnungen können wir die Probe machen, indem wir mit dem entsprechenden Wurzelexponenten, hier also $3$, potenzieren. Das ergibt in diesem Beispiel:
$k=0$:
$\begin{array}{rcl}z_0^3 &=& 2^3\left(\cos\left(3\cdot 0\right)+i\sin\left(3\cdot 0\right)\right) \\ &=& 8\left(\cos\left(0\right)+i\sin\left(0\right)\right) \\ &=&8\end{array}$

$k=1$:
$\begin{array}{rcl}z_1^3 &=& 2^3\left(\cos\left(3\cdot\dfrac{2\pi}{3}\right)+i\sin\left(3\cdot\dfrac{2\pi}{3}\right)\right) \\ &=& 8\left(\cos\left(2\pi\right)+i\sin\left(2\pi\right)\right) \\ &=& 8\left(\cos\left(0\right)+i\sin\left(0\right)\right) \\ &=& 8\end{array}$

$k=2$:
$\begin{array}{rcl}z_2^3 &=& 2^3\left(\cos\left(3\cdot\dfrac{4\pi}{3}\right)+i\sin\left(3\cdot\dfrac{4\pi}{3}\right)\right) \\ &=& 8\left(\cos\left(4\pi\right)+i\sin\left(4\pi\right)\right) \\ &=& 8\left(\cos\left(0\right)+i\sin\left(0\right)\right) \\ &=& 8\end{array}$

Bemerkung: Radizieren ist im Großen und Ganzen nur möglich, wenn die komplexe Zahl in trigonometrischer oder exponentieller Darstellungsweise vorliegt. Selbst wenn man, wie in diesem Beispiel, zumindest einen Anfang in kartesischer Form machen kann, besteht immer die große Gefahr, dass nicht alle Wurzeln gefunden werden.

Da diese $n$-ten Wurzeln alle den gleichen Betrag haben (es ändert sich ja nur der Winkel), liegen sie auf einem Kreis um den Ursprung in der gaußschen Zahlenebene. Wenn man sie mit geraden Linien verbindet, bilden sie ein regelmäßiges $n$-Eck. Das "$2$-Eck", das sich für $n=2$ ergibt, ist eine Strecke.

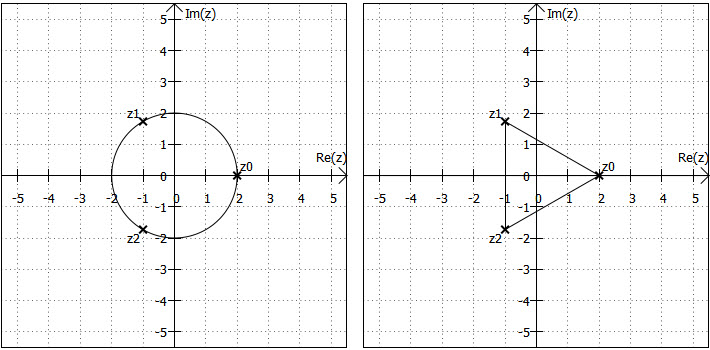
Die erste Wurzel, auf die man stößt, wenn man sich entgegengesetzt des Uhrzeigersinns (mathematisch positiv) durch die gaußsche Zahlenebene bewegt, heißt Hauptwert und wird meist mit $z_0$ bezeichnet. Zwischen den verschiedenen Wurzelwerten liegt jeweils der Winkel $\dfrac{2\pi}{n}$, wobei mit $n$ der Wurzelexponenten gemeint ist.


Bleibt die Frage, warum es ausreicht $k=0,1,...,n-1$ zu betrachten. Der Grund ist, dass sich für $k\geq n$ wieder die gleichen Werte ergeben. Schauen wir uns an, was im obigen Beispiel passieren würde:
$k=3$:
$\begin{array}{rcl}z_3 &=& \sqrt[3]{8}\left(\cos\left(\dfrac{0+2\cdot 3\cdot\pi}{3}\right)+i\sin\left(\dfrac{0+2\cdot 3\cdot\pi}{3}\right)\right) \\ &=& 2\left(\cos\left(2\pi\right)+i\sin\left(2\pi\right)\right) \\ &=& 2\left(\cos\left(0\right)+i\sin\left(0\right)\right) \\ &=& z_0\end{array}$

$k=4$:
$\begin{array}{rcl} z_4 &=& \sqrt[3]{8}\left(\cos\left(\dfrac{0+2\cdot 4\cdot\pi}{3}\right)+i\sin\left(\dfrac{0+2\cdot 4\cdot\pi}{3}\right)\right) \\ \\ &=& 2\left(\cos\left(\dfrac{8\pi}{3}\right)+i\sin\left(\dfrac{8\pi}{3}\right)\right) \\ \\ &=& 2\left(\cos\left(\dfrac{2\pi}{3}\right)+i\sin\left(\dfrac{2\pi}{3}\right)\right) \\ \\ &=& z_1\end{array}$

$k=5$:
$\begin{array}{rcl}z_5 &=& \sqrt[3]{8}\left(\cos\left(\dfrac{0+2\cdot 5\cdot\pi}{3}\right)+i\sin\left(\dfrac{0+2\cdot 5\cdot\pi}{3}\right)\right) \\ \\ &=& 2\left(\cos\left(\dfrac{10\pi}{3}\right)+i\sin\left(\dfrac{10\pi}{3}\right)\right) \\ \\ &=& 2\left(\cos\left(\dfrac{4\pi}{3}\right)+i\sin\left(\dfrac{4\pi}{3}\right)\right) \\ \\ &=& z_2\end{array}$

Sie können sich vermutlich vorstellen, wie es weitergeht ...


Fazit: Die Zahl $z$ hat also genau $n$ komplexe $n$-te Wurzeln. Damit schließt sich der Kreis zum Anfang des Kapitels und dem dort erwähnten Fundamentalsatz der Algebra.

Zum Abschluss

Sie haben (hoffentlich) gemerkt, dass komplexe Zahlen, wenn man einmal dieses $i$ in der Zahl akzeptiert hat, sooooo geheimnisvoll dann auch wieder nicht sind. Natürlich ist dies nur eine ganz grundlegende Einführung, aber der Grundsatz bei Zahlenbereichserweiterungen, dass gewohnte Rechengesetze weiter gelten sollen, bedeutet hier eben auch, dass z. B. der Satz des Pythagoras oder die Definitionen der Trigonometrie hier genauso und unter den gleichen Bedingungen angewendet werden dürfen wie vorher. Warum hätte man das auch ändern sollen?