Dieses Kapitel enthält die folgenden Themen:

• Potenzen - die grundlegende Definition
• Binomische Formeln
• Rechnen mit Potenzen
• Rechnen mit Wurzeln
• Rechnen mit Logarithmen
• Umgang mit Termen

8.2 Potenzen, Wurzeln, Logarithmen - Erklärungen

Wir haben die Grundlagen noch nicht ganz geschafft ... In diesem Kapitel geht es noch einmal um etwas ganz Wichtiges, worauf eigentlich alle weiteren Themen aufbauen: nämlich Terme, die sich aus Potenzen, Wurzeln und Logarithmen zusammensetzen.
Warum ist dieses Kapitel so wichtig? Kommen wir noch mal auf das Fußballbeispiel aus dem Kapitel Rechengesetze zurück: Wir trainieren in diesem Kapitel den zulässigen Umgang mit bestimmten, sehr wichtigen Arten von Termen. Das ist vergleichbar mit einer Fußballmannschaft, die Dribbeln und Standards (wie Elfmeter, Ecken, Einwürfe) einübt und trainiert, wie man der gegnerischen Mannschaft den Ball abnimmt, ohne zu foulen etc. Diese Dinge werden alle trainiert, bevor man das erste 90-Minuten-Match bestreitet, weil man darin die grundlegenden Fußballtechniken sicher beherrschen muss. Fußballspielerinnen und -spielern wird es schwerfallen, am Spielverlauf sinnvoll teilzunehmen, wenn sie sich noch auf das Dribbeln konzentrieren müssen …
Genauso ist es hier: Wir üben den zulässigen Umgang mit Potenzen, Wurzeln und Logarithmen, um diese anschließend in komplexeren Zusammenhängen, wie Gleichungen und Funktionen, sicher anwenden zu können. Sonst ist es kaum möglich, darauf aufbauende Aufgaben zu bewältigen. Wenn Sie beim Lösen einer Exponentialgleichung oder beim Berechnen eines Integrals noch überlegen müssen, wie $e^{2x}\cdot e^{x+1}$ zusammengefasst werden kann, wird es Ihnen schwerfallen, den Gesamtlösungsweg im Blick zu behalten und die berechnete Lösung am Ende zu plausibilisieren.

Potenzen - die grundlegende Definition

Grundlegende Definition einer Potenz: $a^n= \underbrace{a \cdot a \cdot \ldots \cdot a}_n$ für $a \in \mathbb{R}$ und $n \in \mathbb{N}$ ($a^n$ gesprochen: "a hoch n")
Die Potenz $a^n$ ist also erst mal nur eine abkürzende Schreibweise für ein Produkt mit vielen gleichen Faktoren. Das hat den Vorteil, dass man die Faktoren nicht mehr zählen muss ... $a$ heißt dabei Basis (vom griechischen Wort basis für Grundlage) und $n$ Exponent (vom lateinischen Wort exponere, welches herausstellen bedeutet).
Ist der Exponent $2$, sagt man auch Quadrieren.

Beispiele:

Schauen wir uns die Definition noch etwas genauer an: Dort heißt es $a^n$ für $a \in \mathbb{R}$ und $n \in \mathbb{N}$. Das bedeutet, dass die Basis irgendeine reelle und der Exponent eine natürliche Zahl sein muss (zumindest im Moment, weiter unten erweitern wir dies). Ist der Exponent also $2$, $5$, $10$ oder vielleicht auch $4.923$, ergibt sich ein Produkt mit entsprechend vielen Faktoren, wobei diese Faktoren immer reelle Zahlen sind. Ein bisschen aus der Reihe tanzen die Exponenten $1$ und $0$ (zumindest erkennt man dort das Produkt nicht mehr): 

• Wir hatten gerade schon ein entsprechendes Beispiel: $a^1=a$, egal für welche reelle Zahl $a$ steht. "Unmathematisch" formuliert: Man kann den Exponenten in diesem Fall einfach weglassen.
  
  
• Etwas überraschend ist vielleicht diese Festlegung: $a^0=1$ für $a\neq 0$. Anders gesagt: Wenn man eine reelle Zahl ungleich $0$ mit $0$ potenziert, ist das Ergebnis immer $1$ - völlig egal, welche reelle Zahl man potenziert.
  
  
• Bleibt die Frage, was mit $0^0$ ist: $0^0$ ist nicht definiert. Das heißt, hier gibt es keine Vereinfachung und kein Ergebnis.

Ganz wichtig: Im Allgemeinen ist $a \cdot a = a^2 \neq 2a = a+a$.

"Im Allgemeinen" bedeutet dabei, dass es einzelne Zahlenwerte gibt, für die diese Gleichungen gelten, aber für die (überwältigende) Mehrheit der Werte ist $a^2$ eben nicht gleich $2a$. Hierfür ein paar Beispiele:

Und noch ein paar Erkenntnisse zu Potenzen, die später mal helfen können, z. B. wenn man ein Ergebnis auf Plausibilität prüfen möchte:

• Ist der Exponent $n$ eine gerade Zahl, ist die gesamte Potenz immer größer oder gleich $0$, mathematisch formuliert: $a^n \geq 0$
  
  
• Ist die Basis einer Potenz ungleich $0$ (mathematisch aufgeschrieben: $a\neq 0$), ist auch die gesamte Potenz immer ungleich $0$ (auch hier die mathematische Formulierung $a^n\neq 0$).

Vielleicht noch wichtiger: Potenzrechnung geht vor Punktrechnung geht vor Strichrechnung!
Auch hier können ausschließlich Klammern eine andere Reihenfolge der Rechenoperationen festlegen.

Wir hatten im Kapitel Rechengesetze schon mal besprochen, dass die unterschiedlichen Rechenoperationen eine bestimmte Rangfolge erfordern, man also nicht "einfach so" drauf losrechnen darf. Die Regel "Punkt- vor Strichrechnung" gilt hier natürlich immer noch und wird um eine "Ebene", nämlich um die Potenzrechnung, erweitert. Viele typische Fehler aus diesem Kapitel gehen auf dieses Problem zurück. Hier noch ein paar Beispiele dazu:

Je nachdem, wie die Klammen gesetzt wurden, kommen also sehr unterschiedliche Werte heraus. Der letzte ist fast das 2.400-Fache vom ersten! Um Fehler zu vermeiden, lohnt sich also auch hier, sehr sorgfältig zu sein.

Binomische Formeln

Weil eben Potenz- vor Punkt- vor Strichrechnung geht, braucht man spezielle Überlegungen, wenn die verschiedenen Rechenoperationen aufeinandertreffen. Ein bekanntes Beispiel sind die binomischen Formeln beim Zusammentreffen von Addition/Subtraktion und Quadrieren/Multiplizieren:

Beispiele:

Sie bieten eine Art Abkürzung für das Auflösen von speziellen Klammertermen, die sonst mithilfe des Distributivgesetzes ausmultipliziert werden müssten, z. B. $(a+b)^2 = (a+b)(a+b)=a^2+ab+ba+b^2= a^2+2ab+b^2$. Das geht natürlich auch - ist aber länger und damit meist fehleranfälliger.

Ganz wichtig: Egal, welchen Weg man wählt: Das Ergebnis von $(a+b)^2$ ist nicht $a^2+b^2$.

Hier ein paar Rechenbeispiele, um das zu verdeutlichen:

Anders gesagt: Bitte vergessen Sie bei der 1. und 2. binomischen Formel nicht den mittleren Term $2ab$ bzw. $-2ab$. Damit ändern sich die Rechenbeispiele von oben zu:

Das gilt natürlich genauso, wenn Variablen in den Termen enthalten sind - man sieht mögliche Fehler dann nur nicht mehr so schnell.

Binomische Formeln "rückwärts": Häufig ist es nützlich, die binomischen Formeln "von rechts nach links", d. h. zum Faktorisieren, anzuwenden. Wenn man irgendwo kürzen möchte, braucht man ja ein Produkt, welches man auf diesem Weg herstellen kann.

Beispiele:

Hierbei muss man ein bisschen aufpassen, vor allem auf die Struktur des mittleren Terms bei der 1. und 2. binomischen Formel: Die beiden quadratischen Terme am Anfang und Ende sind meist problemlos zu erkennen. Aber diese Umformungen funktionieren wirklich nur, wenn der mittlere Term die Struktur $2ab$ bzw. $-2ab$ hat. Da $(m+9)^2 = m^2+18m+81$, würde sich beispielsweise $m^2+10m+81$ nicht mithilfe der binomischen Formel zusammenfassen lassen und auch mit keiner anderen Formel.
Die 3. binomische Formel funktioniert auch nur dann, wenn einer der quadratischen Terme positiv und einer negativ ist.
Weiter unten wird es noch ein paar komplexere Beispiele geben, nämlich von binomischen Formeln im Zusammenspiel mit Potenzgesetzen.

Von Potenzen zu Wurzeln und Logarithmen

Wir nehmen eine Potenz $a^n$, die irgendein Ergebnis $x$ liefert:

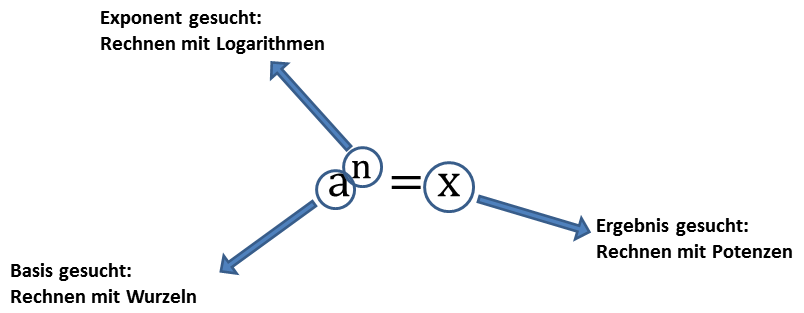
Das Rechnen mit Potenzen gibt Antwort auf die Frage: Welches Ergebnis erhalte ich, wenn ich die Zahl $a$ $n$-mal mit sich selbst multipliziere?

Das Rechnen mit Wurzeln gibt Antwort auf die Frage: Welche Zahl ergibt $x$, wenn ich sie $n$-mal mit sich selbst multipliziere?
Formal geschrieben: $a=\sqrt[n]{x}$

Das Rechnen mit Logarithmen gibt Antwort auf die Frage: Wie oft muss ich die Zahl $a$ mit sich selbst multiplizieren, damit das Ergebnis $x$ ist?
Formal geschrieben: $n=\log_a {x}$

Diese Fragen zeigen es schon: Potenzieren, Radizieren (also das Rechnen mit Wurzeln) und Logarithmieren gehören eng zusammen und heben sich - vorausgesetzt die Basen bzw. die Exponenten sind gleich - gegenseitig auf. Mathematisch sagt man: Sie sind Umkehroperationen. 

In den folgenden Abschnitten wird es nun darum gehen, wie man mit Potenzen, Wurzeln und Logarithmen umgeht und welche Rechengesetze in den einzelnen Fällen gelten. Natürlich werden auch einige Beispiele nicht fehlen.

Rechnen mit Potenzen

Beim Rechnen mit Potenzen benötigt man in erster Linie die fünf Potenzgesetze. Wie alle Rechengesetze können sie sowohl "von links nach rechts" als auch "von rechts nach links" gelesen werden - je nachdem, was sich für die entsprechende Aufgabe anbietet.

1. Potenzgesetz: $a^n \cdot a^m = a^{n+m}$
Merksatz: Potenzen mit gleicher Basis werden multipliziert, indem man die Exponenten addiert.
Beispiel: $5^2 \cdot 5^6 = 5\cdot 5\;\cdot\; 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5 = 5^{2+6} = 5^8$


2. Potenzgesetz: $a^n : a^m = \dfrac{a^n}{a^m} = a^{n-m}$
Merksatz: Potenzen mit gleicher Basis werden dividiert, indem man die Exponenten subtrahiert.
Beispiel: $10^8 : 10^6 = \frac{10^8}{10^6} = 10^{8-6} = 10^2$


3. Potenzgesetz: $\left(a^n\right)^m = a^{n \cdot m}$
Merksatz: Potenzen werden potenziert, indem man die Exponenten multipliziert.
Beispiel: $\left(3^4\right)^5 = 3^{4 \cdot 5} = 3^{20}$


4. Potenzgesetz: $a^n \cdot b^n = \left(a \cdot b \right)^n$
Merksatz: Potenzen mit gleichen Exponenten werden multipliziert, indem man die Basen multipliziert.
Beispiel: $8^2 \cdot 9^2 = \left(8 \cdot 9 \right)^2 =72^2$


5. Potenzgesetz: $a^n : b^n = \dfrac{a^n} {b^n} = \left(\dfrac{a}{b}\right)^n$
Merksatz: Potenzen mit gleichen Exponenten werden dividiert, indem man die Basen dividiert.
Beispiel: $14^3 : 7^3 = \frac{14^3} {7^3} = \left(\frac{14}{7}\right)^3 = 2^3$ 

Worauf man unbedingt achten muss:
Das 4. Potenzgesetz "von rechts nach links" gelesen besagt $\left(a \cdot b \right)^n = a^n \cdot b^n$. Das bedeutet: Steht eine Basis (bestehend aus mehreren Faktoren) in Klammern, müssen alle Bestandteile der Basis potenziert werden! Und umgekehrt: Steht diese Basis nicht in Klammern, darf nur der Faktor potenziert werden, der den Exponenten trägt. Ein Beispiel:

Ob $a^n \cdot b^n$ oder $a \cdot b^n$ gerechnet wird, macht also offensichtlich einen Unterschied. Die Klammern sind hier - mal wieder - sehr wichtig!

Aus dem gleichen Grund ist auch $(-4)^2$ nicht das Gleiche wie $-4^2$. Um genau zu sein:

Im ersten Fall wird das Minuszeichen mit quadriert, im zweiten nicht. Auch wenn das auf den ersten Blick eher unpraktisch erscheint, haben beide Varianten ihre Berechtigung. Daher muss man sie (durch den Einsatz von Klammern) sorgfältig unterscheiden.

Ganz wichtig: Es gibt keine Potenzgesetze für die Addition/Subtraktion von Potenzen!
Das bedeutet, dass Addition und Subtraktion nichts am Exponenten einer Potenz ändern können. Diese Tatsache wird (hoffentlich) einleuchtend, wenn man sich überlegt, dass Potenzen "Abkürzungen" für Produkte mit vielen gleichen Faktoren sind. Produkte gehören zur Punktrechnung und gehen damit vor jede Addition/Subtraktion!
Die Addition/Subtraktion von Potenzen ist also nur möglich, wenn alle Basen und alle Exponenten in der Summe/Differenz gleich sind - und sie kann nur etwas am Koeffizienten der Potenz ändern (siehe Rechnen mit Variablen).

Ein paar Beispiele:

Kommen wir jetzt noch mal zurück zu den binomischen Formeln: Bislang waren die Beispiele alle von der Struktur her recht einfach. Interessanter wird es, wenn Zahlen und Variablen gemeinsam in binomischen Formeln auftreten. Schauen wir uns dazu ein paar Beispiele an:

Sie sehen, dass diese Rechnungen auch mit so wenig Regeln (Wurzeln und Logarithmen kommen ja erst ...) schon ganz schön komplex werden können. Umso wichtiger ist es, diese Regeln gut zu verinnerlichen und einzuüben. Sie werden sie brauchen!

Nun gehen wir einen Schritt weiter:
Ganz oben wurde erklärt, dass Potenzen $a^n$ für $a \in \mathbb{R}$ und $n \in \mathbb{N}$ definiert sind - und auch schon in Aussicht gestellt, dass es für diese Definitionsbereiche noch Erweiterungen geben wird. Darum wollen wir uns jetzt kümmern.
Um eine der Erweiterungen herzuleiten, schauen wir uns ein Beispiel an: Nehmen wir $\frac{5^2}{5^4}=5^{2-4}=5^{-2}$. Hier wurde das 2. Potenzgesetz angewendet. Schreiben wir stattdessen die Potenz aus und kürzen ein bisschen, erhalten wir $\frac{5^2}{5^4}=\frac{5\cdot 5}{5\cdot 5\cdot 5\cdot 5}=\frac{1}{5\cdot 5}=\frac{1}{5^2}$. Offensichtlich ist $5^{-2} = \frac{1}{5^2}$ ist. Allgemein aufgeschrieben:
$a^{-n} = \dfrac{1}{a^n}$ mit $a \in \mathbb{R}\backslash_{\{0\}}$ und $n \in \mathbb{Z}$
Potenzen können also auch negative Exponenten haben. Anders gesagt: Die Exponenten können aus dem Zahlenbereich der ganzen Zahlen $\mathbb{Z}$ stammen. $a^{-n}$ bedeutet dabei nicht, dass der Potenzausdruck negativ wird (Dazu müsste das Minuszeichen vor der Potenz stehen!), sondern dass der Kehrwert von $a^n$ gebildet wird. Da die Potenz damit in den Nenner gelangt, darf die Basis natürlich nicht $0$ sein.
Wichtig: Das 4. Potenzgesetz gilt natürlich auch, wenn der Exponent negativ ist. Ein paar Beispiele:

Die folgende Erweiterung bringt uns nun direkt zum nächsten Abschnitt dieses Kapitels.

Rechnen mit Wurzeln

Potenzen können nicht nur negative, sondern auch gebrochene Exponenten haben:
$\displaystyle{ a^{\frac{1}{n}} = \sqrt[n]{a}}$ (gesprochen: "n-te Wurzel aus a") mit $a \in \mathbb{R}^+_0$, wenn $n \in \mathbb{N}^+$ gerade, oder $a \in \mathbb{R}$, wenn $n \in \mathbb{N}^+$ ungerade
$n$ heißt Wurzelexponent und ist eine natürliche Zahl (mit Ausnahme von $0$). $a$ heißt Radikand und ist eine (nichtnegative) reelle Zahl.

Diese Potenzschreibweise einer Wurzel mag einem auf den ersten Blick merkwürdig oder unpraktisch vorkommen - sie hat aber große Vorteile! Der größte: Durch sie gelten auch für Wurzeln die oben aufgeführten Potenzgesetze. Man benötigt also für das Rechnen mit Wurzeln keine zusätzlichen Regeln (auch wenn sie in vielen Formelsammlungen aufgeführt sind ...). Außerdem wird der Zusammenhang zwischen Potenzen und Wurzeln sehr gut deutlich. Und nicht zuletzt: Beim Ableiten und Integrieren kommt man ohne diese Schreibweise quasi nicht aus. Es ist also günstig, sich jetzt schon mal daran zu "gewöhnen".

Bemerkung: Solange keine Missverständnisse auftreten können, spricht man von "Wurzel" statt von "2. Wurzel" bzw. "Quadratwurzel" und schreibt $\sqrt{x}$ statt $\sqrt[2] {x}$.Trotzdem geht die $2$ natürlich nicht verloren ...

Beispiele:

 
Ein paar allgemeinere Erkenntnisse zu Wurzeln:
Wurzeln verhalten sich unterschiedlich, je nachdem, ob der Wurzelexponent gerade oder ungerade ist:

• Bei geraden Wurzelexponenten:
  • Da es keine reelle Zahl gibt, die mit sich selbst multipliziert ein negatives Ergebnis, wie $-4$, ergibt, können aus negativen Zahlen keine Quadratwurzeln gezogen werden. Da "minus mal minus gleich plus" ist, gilt diese Erkenntnis für alle Wurzeln mit geraden Wurzelexponenten. Klassischerweise formuliert man: Aus negativen reellen Zahlen können keine Wurzeln mit geraden Wurzelexponenten gezogen werden!
  • Solche Wurzeln sind immer größer oder gleich $0$, mathematisch formuliert: $\sqrt[n]{x} \geq 0$.
    Das hat eine wichtige Folge: Da beim Quadrieren möglicherweise negative Vorzeichen "verloren" gehen, erhält man beim Wurzelziehen aus quadratischen Termen den Betrag des Radikanden: $\sqrt{x^2} = \vert x \vert$ (analog für höhere Exponenten und Wurzelexponenten). Wir wissen ja nicht, ob das $x$ vor dem Quadrieren positiv oder negativ gewesen ist ...
    
    
• Bei ungeraden Wurzelexponenten:
  • Multipliziert man eine negative reelle Zahl so mit sich selbst, dass man eine ungerade Anzahl von Faktoren hat, ist das Ergebnis negativ (Es bleibt ja quasi ein Minuszeichen "übrig" ...), z. B. $-2\cdot (-2)\cdot (-2) = (-2)^3=-8$. Daher können Wurzeln mit ungeraden Wurzelexponenten aus negativen Zahlen gezogen werden.
    Aus mathematischen Gründen formuliert man: Ist $n$ ungerade und $a$ negativ, gilt: $\sqrt [n]{a}= -\sqrt[n]{\vert a \vert}$.
  • Solche Wurzeln können dann auch negative Ergebnisse haben. Zum Beispiel ist $\sqrt[3]{-8}=-\sqrt[3]{\vert-8\vert}=-2$.

Die nächste Frage ist nun natürlich: Wie rechnet man mit Wurzeln eigentlich? Dazu schauen wir uns die Potenzgesetze noch mal an:

1. Potenzgesetz: $a^n \cdot a^m = a^{n+m}$
Beispiel: $\sqrt[5]{(2z)^3}\cdot\sqrt[5]{(2z)^2} = (2z)^\frac{3}{5}\cdot (2z)^\frac{2}{5} = (2z)^{\frac{3}{5}+\frac{2}{5}} = (2z)^1 = 2z$ mit $z\in \mathbb{R}^+_0$
Wichtig: Klammern um $2z$ nicht vergessen!


2. Potenzgesetz: $a^n : a^m = \frac{a^n}{a^m} = a^{n-m}$
Beispiel: $\dfrac{\sqrt[3]{a}}{\sqrt{a^9}} = \dfrac{a^\frac{1}{3}}{a^\frac{9}{2}} = a^{\frac{1}{3}-\frac{9}{2}} = a^{-\frac{25}{6}} = \dfrac{1}{a^\frac{25}{6}} = \dfrac{1}{\sqrt[6]{a^{25}}}$ mit $a\in \mathbb{R}^+$
Wichtig: Bei der Nenner-Potenz die $2$ im Exponenten nicht vergessen! Es handelt sich ja um eine 2. Wurzel, auch wenn der Wurzelexponent nicht hingeschrieben wurde.


3. Potenzgesetz: $\left(a^n\right)^m = a^{n \cdot m}$
Beispiel 1: $\left(\sqrt{s^3}\right)^4 = \left(s^\frac{3}{2}\right)^4 = s^{\frac{3}{2}\cdot 4} = s^\frac{12}{2} = s^6$ mit $s\in \mathbb{R}^+_0$
Wichtig: Auch hier die $2$ im Exponenten nicht vergessen!

Beispiel 2: $x^\frac{2}{5} = x^{2\cdot\frac{1}{5}} = \left(x^2\right)^\frac{1}{5} = \sqrt[5]{x^2}$ mit $x\in \mathbb{R}$
Bemerkung: Diese Umformung kann man auch von rechts nach links anwenden.


4. Potenzgesetz: $\left(a \cdot b \right)^n = a^n \cdot b^n$
Beispiel: $\sqrt{4\cdot y} = \sqrt{4}\cdot\sqrt{y} = 2\cdot\sqrt{y}$ mit $y\in \mathbb{R}^+_0$
Bemerkung: Diese Vorgehensweise nennt man auch "teilweises Wurzelziehen". Damit kann man Wurzelterme häufig noch ein gutes Stück vereinfachen.


5. Potenzgesetz: $\left(\frac{a}{b}\right)^n = a^n : b^n = \frac{a^n} {b^n}$
Beispiel: $\sqrt[3]{\dfrac{p^3}{8}} =\dfrac{\sqrt[3]{p^3}}{\sqrt[3]{8}} = \dfrac{p^{3\cdot\frac{1}{3}}}{2} = \dfrac{p^1}{2} = \dfrac{p}{2}$ mit $p\in \mathbb{R}$
Bemerkung: Werte wie $\sqrt[3]{8}$ dürfen natürlich einfach ausgerechnet werden.

Erkenntnisse aus diesen Beispielen:

• Natürlich können Potenzen auch Exponenten haben, die negativ und gebrochen sind. Dann werden einfach beide Regeln nacheinander angewendet (siehe Beispiel zum 2. Potenzgesetz).
  
  
• Radizieren (das "offizielle" Wort für Wurzelziehen) und Potenzieren mit dem gleichen Exponenten heben einander auf (siehe Beispiel zum 5. Potenzgesetz). Achten Sie aber darauf, dass bei geraden Wurzelexponenten ggf. ein Betrag nötig wird, da solche Wurzelterme ja immer nichtnegativ sein müssen.
  
  
• Da es nur diese fünf Potenzgesetze gibt, lassen sich auch Wurzeln oder Vielfache von Wurzeln ausschließlich dann addieren und subtrahieren, wenn sie gleiche Wurzelexponenten und gleiche Radikanden haben! Siehe oben ...

Ganz wichtig: Aus Summen können keine Wurzeln gezogen werden!
Anders formuliert: Wurzeln aus Summen lassen sich im Allgemeinen nicht vereinfachen, insbesondere ist $\sqrt{a +b} \neq \sqrt{a}+\sqrt{b}$ für fast alle $a$ und $b$!

Wie oben, ein paar Beispiele hierfür:

Bitte beachten Sie, dass sich in der zweiten Zeile einmal eine irrationale Zahl, d. h. eine unendliche, nichtperiodische Dezimalzahl, und einmal eine natürliche Zahl als Ergebnis ergibt. Die Ergebnisse können also schon aus formalen Gründen nicht gleich sein! Allgemein gilt: Betrachtet man nur natürliche Zahlen im Radikanden, sind Wurzeln aus Quadratzahlen, wie $1$, $4$, $9$ etc., wieder natürliche Zahlen; Wurzeln aus Nicht-Quadratzahlen, wie $2$, $3$, $5$ etc., sind irrationale Zahlen.

Rechnen mit Logarithmen

Kümmern wir uns um die letzte Rechenart in diesem Zusammenhang: den Logarithmus $\log_a(x)$. Wobei es eigentlich nicht den einen Logarithmus gibt, sondern viele, da ja nicht festgelegt ist, welche Zahl $a$ ist. Für den Umgang mit Logarithmen macht das aber keinen Unterschied, nur fürs Ausrechnen am Ende ...

Der Logarithmus $\log_a(x)$ (gesprochen: "Logarithmus zur Basis a von x") ist definiert für $a \in \mathbb{R}^+\backslash_{\{1\}}$ und $x \in \mathbb{R}^+$.
$a$ heißt Basis und $x$ Argument des Logarithmus (oder kurz: Argument). Teilweise sagt man statt Argument auch Numerus.
Wichtig: Da das Argument eines Logarithmus positiv sein muss, sind Ausdrücke wie $\log_a(0)$ oder $\log_a\left(-x^2\right)$ unmöglich.

Für alle, die es genauer wissen möchten, wird im nächsten Abschnitt erklärt, warum diese Einschränkungen für die Basis und das Argument gelten. Alle anderen dürfen diesen Abschnitt überspringen und gleich mit den Hinweisen zur Schreibweise weitermachen ...

• Potenzen mit negativen Basen sind im Bereich der reellen Zahlen nur für ganzzahlige Exponenten definiert. Das heißt: Ein Term wie $(-2)^{\frac{1}{2}}=\sqrt{-2}$ liefert kein Ergebnis. Genau dieses Ergebnis bräuchte der Logarithmus aber als Argument. Also geht das Ganze nur mit positiven Basen.
  
  
• Ein Potenzausdruck mit der Basis $1$ wäre eine ziemlich langweilige Angelegenheit, denn $1^n = 1$, egal welche reelle Zahl $n$ ist. Betrachtet man umgekehrt den Logarithmus, also die Frage, wie oft die Basis $1$ mit sich selbst multipliziert werden muss, damit das Ergebnis $1$ ist, gibt es darauf keine eindeutige Antwort. Da es in der Mathematik wenig Fans von uneindeutigen Antworten gibt (sie sind auch meist nicht sinnvoll), schließt man $1$ als Basis aus.
  
  
• Wenn die Basis positiv ist, kann das Ergebnis des Potenzausdrucks nie negativ oder $0$ werden, denn für negative Exponenten gilt ja $a^{-n} = \frac{1}{a^n}$ und das ist in diesem Fall immer größer als $0$. Da der Logarithmus genau dieses Ergebnis als Argument verwendet, kommen also nur positive Argumente infrage.

Noch ein paar Hinweise zur Schreibweise:

• Teilweise werden (aus Faulheit ...) beim Logarithmus die Klammern weggelassen, beispielsweise $\log_a(x) = \log_a x$. Das ist aber nicht immer möglich: Bei $\log_ay+9$ könnte sowohl $\log_a(y)+9$ als auch $\log_a (y+9)$ gemeint sein. Damit Missverständnisse ausgeschlossen sind, müssen hier unbedingt Klammern gesetzt werden. Sie haben also die nächste Stelle kennengelernt, wo man sehr, sehr gut auf die Klammern achtgeben sollte!
  
  
• Mit der Basis ist es ähnlich: Man schreibt beispielsweise $\log(x)$ und meint $\log_a(x)$. Das ist dann ok, wenn die Umformung allgemein für alle Basen gilt oder wenn klar ist, um welche Basis es sich handelt. Spätestens, wenn es um das Ausrechnen von Zahlenwerten geht, muss man die Basis aber nennen. Die Antworten auf die folgenden Fragen sind ja offensichtlich nicht gleich:
  
  • Wie oft muss ich die Zahl $2$ mit sich selbst multiplizieren, damit das Ergebnis $10$ ist? Antwort: ca. $\log_2(10) = 3{,}32$, denn $2^{3{,}32} \approx 10$
  • Wie oft muss ich die Zahl $10$ mit sich selbst multiplizieren, damit das Ergebnis $10$ ist? Antwort: $\log_{10}(10) = 1$, denn $10^1 = 10$

Leider gibt es für Logarithmen keine so praktische Umschreibung in Potenzschreibweise wie bei den Wurzeln (alle möglichen Potenzen sind ja schon "verbraucht" ...), sodass man hier wirklich zusätzliche Rechengesetze benötigt. Darum geht es nun im folgenden Abschnitt.

Logarithmengesetze

Für das Rechnen mit Logarithmen gelten die folgenden Logarithmengesetze. Wie auch die Potenzgesetze können sie sowohl "von links nach rechts" als auch "von rechts nach links" gelesen werden - je nachdem, was sich für die entsprechende Aufgabe anbietet.

1. Logarithmengesetz: $\log_a(x \cdot y) = \log_a(x) + \log_a(y)$
Merksatz: Der Logarithmus eines Produkts ist gleich der Summe der Logarithmen der einzelnen Faktoren.
Beispiel: $\log_{10}(10x) = \log_{10}(10)+\log_{10}(x) = 1+\log_{10}(x)$


2. Logarithmengesetz: $\log_a\left(\dfrac{x}{y}\right) = \log_a(x) - \log_a(y)$
Merksatz: Der Logarithmus eines Quotienten ist gleich der Differenz aus dem Logarithmus des Dividenden und dem Logarithmus des Divisors.
Beispiel: ${\log_2\left(\frac{a}{0{,}5}\right) = \log_2(a)-\log_2(0{,}5) = \log_2(a)-\log_2\left(\frac{1}{2}\right) = \log_2(a)-\log_2\left(2^{-1}\right) = \log_2(a)-(-1) = \log_2(a)+1}$


3. Logarithmengesetz: $\log_a\left(x^k\right) = k \cdot \log_a(x)$
Merksatz: Der Logarithmus einer Potenz ist gleich dem Produkt aus dem Exponenten und dem Logarithmus der Basis.
Beispiel 1: $\log_{100}\left(m^{17}\right) = 17\cdot\log_{100}(m)$
Beispiel 2: $\log_5\left(25^{x+1}\right) = (x+1) \cdot \log_5(25) = (x+1)\cdot 2 = 2x+2$
Bemerkung: Achten Sie im Beispiel 2 - ganz wichtig - darauf, dass Klammern um den Exponenten gesetzt werden müssen!

Vielleicht kommen Ihnen die Logarithmengesetze fremd vor ... Der Logarithmus war aber aufgrund genau dieser Gesetze lange Zeit eine sehr, sehr nützliche und angesehene Rechenart. Wenn Sie sich die drei Gesetze anschauen, sehen Sie nämlich, dass jeweils die Rechenart einfacher wird:

1. Logarithmengesetz: Aus einem Produkt wird eine Summe.
2. Logarithmengesetz: Aus einem Quotienten wird eine Differenz.
3. Logarithmengesetz: Aus einer Potenz wird ein Produkt.

Bevor es Taschenrechner und Computer gab, war dies eine immense Erleichterung!

Um das Ganze etwas plausibler zu machen:
Nach dem 1. Logarithmengesetz ist $\log_a(x)+ \log_a(x) = \log_a(x\cdot x) = \log_a\left(x^2\right)$. Alternativ können Sie natürlich auch rechnen $\log_a(x)+ \log_a(x) = 2\log_a(x) = \log_a\left(x^2\right)$. Hier kommen - zusätzlich zu den Logarithmengesetzen - die "guten alten" Rechenregeln aus Kapitel 5.2 zum Tragen.
Ähnlich ist nach dem 2. Logarithmengesetz $\log_a(x)-\log_a(x) = \log_a\left(\dfrac{x}{x}\right) = \log_a(1) = 0$. Alternativ können Sie natürlich auch argumentieren, dass das Ergebnis immer $0$ ist, wenn man zwei gleiche Werte voneinander subtrahiert.

Ganz wichtig: Die drei genannten Logarithmengesetze sind die einzigen Gesetze für das Rechnen mit Logarithmen!
Das bedeutet:
1. Steht im Argument ein Produkt, ein Quotient oder eine Potenz, kann man dies nur genau so zusammenfassen, wie hier gezeigt wurde. Klammern inklusive …
2. Steht im Argument eine andere Rechenoperation, z. B. eine Summe oder eine Differenz, kann man den Term nicht weiter umformen.

Ebenfalls ganz wichtig: Alle anderen Rechenregeln, die Sie bislang kennengelernt haben (z. B. Punkt vor Strich, Ausklammern, Bruchrechenregeln, binomische Formeln), gelten auch dann, wenn Logarithmen in einer Rechnung auftauchen!

Ein Beispiel mit Zahlen:
$\begin{array}{rclcl} \log_{10}(1.000\cdot 100) &=& \log_{10}(1.000)+\log_{10}(100) &\vert& \text{1. Logarithmengesetz} \cr&=& \log_{10}(10^3)+\log_{10}(10^2) \cr&=& 3+2 \cr&=& 5 \end{array}$
Alternativ kann man rechnen:
$\begin{array}{rclcl} \log_{10}(1.000\cdot 100) &=& \log_{10}(100.000) \cr&=& \log_{10}(10^5) \cr&=& 5 \end{array}$

An dieser Rechnung sehen Sie auch, dass $\log_{10}(1.000\cdot 100) = 5$ nicht das Gleiche ist wie $\log_{10}(1.000) \cdot \log_{10}(100) = 3\cdot 2 = 6$. Das 1. Logarithmengesetz besagt ja aber auch, dass nicht multipliziert, sondern addiert werden muss ...

Außer in solchen Spezialfällen kann man Logarithmen - ähnlich wie Wurzeln - im Kopf häufig nur abschätzen. Sie dürfen, wenn es um das Ausrechnen konkreter Werte geht, also ruhig Ihren Taschenrechner fragen …

Da die Logarithmengesetze vermutlich vielen nicht vertraut sind, sollten wir uns einige Fälle, die ähnlich aussehen, aber sorgfältig unterschieden werden müssen, genauer anschauen:

Die gleichen Fälle müssen unterschieden werden, wenn nicht addiert und multipliziert, sondern subtrahiert und dividiert wird. Ein kleiner "Stolperstein" kommt hinzu: $-\log_a(x)-\log_a(y)-\log_a(z) = \log_a\left(\dfrac{1}{x\cdot y\cdot z}\right)$. Alle Argumente müssen (wegen des Minuszeichens vor den Logarithmen) in den Nenner. Der Zähler kann aber natürlich nicht leer bleiben. Dass es eine $1$ im Zähler sein muss, hat den gleichen Grund, wie beim "normalen" Bilden eines Kehrwertes. Der Kehrwert von $5$ ist ja beispielsweise $\frac{1}{5}$.

Achtung: Keine dieser Rechenoperationen funktioniert, wenn die Basen unterschiedlich sind. Z. B. ist $\log_a(x)+\log_b(y)+\log_a(z) = \log_a(xz)+\log_b(y)$. Potenzen mit unterschiedlichen Basen kann man ja auch nicht zusammenfassen ...

Dann muss man noch etwas aufpassen, wenn Logarithmen mit anderen Rechenoperationen kombiniert werden, was ja meist der Fall ist:

• $\log_a\left(5x^2\right) \neq 2\log_a(5x)$, sondern $\log_a\left(5x^2\right) = \log_a(5)+2\log_a(x)$
  Das Quadrat bezieht sich nur auf die Variable $x$ und nicht auf den Koeffizienten $5$. Wenn man $2\log_a(5x)$ "zurückumformt", ergibt sind $2\log_a(5x) = \log_a\left((5x)^2\right) = \log_a\left(25x^2\right)$.
  
  
• $8\log_a(x\cdot y) \neq 8\log_a(x)+\log_a(y)$, sondern $8\log_a(x\cdot y) = 8\left(\log_a(x)+\log_a(y)\right) = 8\log_a(x)+8\log_a(y)$
  Der Koeffizient $8$ bezieht sich auf den gesamten Logarithmus und damit auf beide Argumente. Das muss auch dann so bleiben, wenn es nach dem Umformen zwei Logarithmenterme mit jeweils einem Argument gibt. Ebenso müssen Klammern gesetzt werden, wenn statt dem 1. das 2. Logarithmengesetz angewendet wird.

In beiden Fällen hat das "Aufpassen-Müssen" eigentlich weniger mit Logarithmen zu tun, sondern vielmehr mit der Rechenregel Potenz- geht vor Punkt- geht vor Strichrechnung. Sie werden es schon gemerkt haben, dass die Mathematik ziemlich pingelig ist, was das angeht ...

Erkenntnisse aus den Beispielen und darüber hinaus:

• Wichtig: Der Logarithmus selbst (also das "Ergebnis") kann trotz der Einschränkungen für Basis und Argument durchaus negativ oder nicht ganzzahlig sein (siehe Beispiel zum 2. Logarithmengesetz). Der Logarithmus ist ja die Frage nach dem Exponenten, und dass es negative oder gebrochene Exponenten geben kann, haben wir in diesem Kapitel an verschiedenen Stellen gesehen.
  
  
• Logarithmieren und Potenzieren mit der gleichen Basis heben einander auf. Sie "beantworten" ja genau die gegenteiligen Fragen: $\log_a\left(a^x\right) = x$ (siehe Beispiel zum 1. Logarithmengesetz). Ein Spezialfall davon ist: $\log_a\left(a\right) = \log_a\left(a^1\right) =1$
  
  
• Umgekehrt funktioniert es genauso: $a^{\log_a(x)} = x$
  
  
• Egal, welche Basis wir betrachten: $\log_a(1) = 0$
  Denn es ist ja $a^0=1$ für alle Basen $a$, die wir hier betrachten.

Noch ein letztes Rechengesetz zum Logarithmus, die sogenannte Basistransformation: $\log_b(x) = \dfrac{\log_a(x)}{\log_a(b)}$
Der Bruch auf der rechten Seite sieht zwar kompliziert aus ... Der Nenner $\log_a(b)$ ist aber einfach nur eine Zahl. Insofern wird das Ganze auch nicht komplizierter, als es ohnehin schon war. Diese Umrechnung wird u. a. gebraucht, wenn

• $b$ eine ungewöhnliche Basis für den Logarithmus ist.
• in einer Rechnung mehrere Logarithmen mit unterschiedlichen Basen auftreten.

Dieses Gesetz ermöglicht es, eine beliebige andere Zahl $a$ (mit den genannten Einschränkungen) zur Basis des Logarithmus zu machen. Man "transformiert" also die Basis. Dadurch kann man z. B.

• eine Basis wählen, mit der der Taschenrechner umgehen kann. Die meisten Taschenrechner "kennen" nämlich nur die Basen $e$ und $10$.
• alle Basen in einer Rechnung vereinheitlichen, damit man die Logarithmen dann mithilfe der Logarithmengesetze zusammenfassen kann (siehe oben).

Namenskonventionen

Einige Logarithmen, die man besonders häufig braucht, haben spezielle Namen bekommen:

• Zweierlogarithmus oder logarithmus dualis: $\log_2(x) = \text{ld}(x)$
  Der Zweierlogarithmus wird u. a. in der Informatik für Rechnungen im Binärsystem verwendet.
• Natürlicher Logarithmus oder logarithmus naturalis: $\log_e(x) = \ln(x)$
  Der natürliche Logarithmus hängt eng mit Wachstumsprozessen und der Zinsrechnung zusammen.
• Zehnerlogarithmus oder dekadischer Logarithmus: $\log_{10}(x) = \lg(x)$
  Der Zehnerlogarithmus spielt beispielsweise bei der Berechnung des pH-Werts und der Bestimmung der Erdbebenstärke auf der Richterskala eine Rolle.

Ein paar Worte noch zum natürlichen Logarithmus: Er ist vermutlich der am häufigsten verwendete Logarithmus. Das liegt wohl daran, dass er eng mit der e-Funktion zusammenhängt, die wiederum beim Ableiten/Integrieren sehr angenehme Eigenschaften hat. Seine Basis ist die nach dem Schweizer Mathematiker Leonhard Euler benannte eulersche Zahl $e = 2{,}718281828459...$, wie $\pi$ eine irrationale Zahl. Man erhält sie z. B. aus dieser unendlichen Rechnung:
${\large e = 1 \,+ \,\frac{1}{1} \,+ \,\frac{1}{1 \cdot 2} \,+ \,\frac{1}{1 \cdot 2 \cdot 3} \,+ \,\frac{1}{1 \cdot 2 \cdot 3 \cdot 4} \,+ \,\frac{1}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5} \,+ \,\frac{1}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6} \,+ \,\frac{1}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7} \,+ \,\dots}$

Wichtig: So verlockend es auch sein mag: $\ln\left(e^x+2\right)$, $\ln\left (e^{2x}-e^x\right)$ und ähnliche Terme lassen sich nicht vereinfachen, da im Argument eine Summe bzw. eine Differenz steht.

Termumformungen

Wir hatten "Terme" im Kapitel Lineare Gleichungen definiert als "eine mathematisch sinnvolle Kombination aus Zahlen, Konstanten, Variablen, Klammern und Rechenoperationen". Durch die Konzepte dieses Kapitels sind viele neue Möglichkeiten, Terme zu definieren, hinzugekommen, die alle an der einen oder anderen Stelle gebraucht werden. Hier zum Abschluss noch ein paar Überlegungen für den Anwendungsfall:

Schreibkonventionen

In Termen ist es üblich:

• Zahlen an den Anfang zu schreiben
• Variablen (auch in Produkten) alphabetisch zu ordnen
• bei Potenzen die Variablen mit dem höchsten Exponenten zuerst zu schreiben

Diese Punkte haben keine mathematische Bedeutung, helfen aber dabei, den Überblick zu behalten - und das ist ja immer gut ...

Was darf man mit Termen machen?

Man darf:

• Zahlen einsetzen und den sich ergebenden Wert ausrechnen
• einen Term in andere einsetzen
• Terme vergleichen
• Terme vereinfachen

Wichtig: Man muss immer darauf achten, nur mit Werten zu hantieren, für die der Term definiert ist. Für Wurzeln und Logarithmen wurden die Definitionsbereiche oben auf dieser Seite beschrieben. Zusätzlich muss man noch aufpassen, dass nicht durch $0$ dividiert wird.

Noch eine Art Vokabel: Man sagt "ein Term nimmt einen speziellen Wert an", wenn das Einsetzen von irgendeiner Zahl zu diesem speziellen Wert führt, z. B. nimmt der Term $\frac{x^2}{x-4}$ für $x=1$ den Wert $-\frac{1}{3}$ an. Für $x=4$ ist der Term $\frac{x^2}{x-4}$ nicht definiert, weil bei diesem Wert der Nenner $0$ würde.

Verfahren zur Termvereinfachung

Terme zu vereinfachen, ist vermutlich der häufigste Anwendungsfall - und wahrscheinlich auch einer der schwierigsten ... Es gibt nämlich zum Vereinfachen von Termen viele verschiedene Verfahren und Rechengesetze, wie ja vermutlich in diesem Kapitel deutlich wurde. Daneben können folgende Gesetz und Regeln helfen:

• Kommutativgesetz
• Assoziativgesetz
• Distributivgesetz
• Erweitern
• Kürzen
  Dabei auf folgende zwei Einschränkungen achtgeben:
  
  1. Aus Summen darf nicht gekürzt werden!
  2. Aus Potenzen darf nur gekürzt werden, wenn die Basen gleich sind!
• ...

Schauen wir uns die beiden Einschränkungen beim Kürzen noch etwas genauer an:

zu 1.
Im Kapitel Bruchrechnung hatten wir schon mal betrachtet, was passiert, wenn man aus Summen kürzt: Das Ergebnis ist dann falsch! Genauso verhält es sich, wenn die Brüche Variablen enthalten - man sieht die Fehler dann nur nicht so schnell. Beispiel: Schauen wir uns den Bruch $\dfrac{5+x}{x}$ an. Wenn man hier $x$ einfach herausstreichen würde, bleibt als Ergebnis nur die $5$. Warum das nicht stimmen kann, sieht man, wenn man für das $x$ verschiedene Zahlenwerte einsetzt: Dann erhält man nämlich auch verschiedene Ergebnisse, beispielsweise

Die Unterschiede sind offensichtlich, was (hoffentlich) klar macht, dass man wirklich nicht aus Summer kürzen darf …

Etwas anderes ist es, wenn der Bruch $\dfrac{5\cdot x}{x}$ lautet. Dann darf das $x$ gekürzt werden, weil ja hier nur Punktrechnung aufeinandertrifft. Auch hierzu ein paar Beispiele:

Ganz wichtig: Bei diesen Rechnungen scheint der Bruch zu "verschwinden", aber es ist ja $5 = \dfrac{5}{1}$. Der Bruch versteckt sich also nur etwas ... Bei $\dfrac{x}{3x} = \dfrac{1}{3}$ darf man auf keinen Fall die $1$ im Zähler vergessen! Ob man $\dfrac{1}{3}$ Kuchen hat oder $3$ ist ja ein deutlicher Unterschied …

zu 2.
Haben Potenzen im Zähler und im Nenner unterschiedliche Basen, darf nicht gekürzt werden, auch nicht im Exponenten! Dazu ein Beispiel: $\dfrac{x^4}{y^2}$ ist im Allgemeinen nicht das gleiche wie $\dfrac{x^2}{y}$, denn $\dfrac{x^4}{y^2} = \dfrac{x\cdot x\cdot x\cdot x}{y\cdot y} \; \neq \; \dfrac{x\cdot x}{y} = \dfrac{x^2}{y}$. Das wird spätestens dann deutlich, wenn statt der Variablen Zahlenwerte im Bruch stehen: $\dfrac{5^4}{3^2} = \dfrac{5 \cdot 5\cdot 5\cdot 5}{3\cdot 3} \; \neq \; \dfrac{5\cdot 5}{3} = \dfrac{5^2}{3}$. Wahrscheinlich würde hier auch niemand auf die Idee kommen zu kürzen, da Zähler und Nenner ja offensichtlich nicht die gleichen Faktoren enthalten. Sind Variablen in einem Bruch enthalten, wissen wir nicht, ob sie für Zahlenwerte mit gleichen Faktoren stehen oder nicht. Daher darf in diesem Fall nicht gekürzt werden.
Das gilt natürlich ebenso, wenn die Terme in Zähler und Nenner komplexer werden, z. B. $\dfrac{3x^2}{(x-5)^2} = \dfrac{3\cdot x \cdot x}{(x-5)\cdot(x-5)} = \dfrac{3\cdot x \cdot x}{25-10x+x^2}$. Und das ist eben nicht das gleiche wie $\dfrac{3x}{x-5}$, was man erhielte, wenn man bei $\dfrac{3x^2}{(x-5)^2}$ die Quadrate "wegkürzen" würde.
Insofern: Man darf aus Exponenten kürzen - aber nur dann, wenn die Basen gleich sind, weil die Basis den Faktor bestimmt und der Exponent "nur" festlegt, wie häufig dieser Faktor mit sich selbst multipliziert wird.

Schwierig ist das Vereinfachen von Termen vor allem deswegen, weil nicht allgemein gesagt werden kann, welche Form des Terms die geschickteste ist. Das hängt stark von der gegebenen Aufgabe ab, z. B. ist es zum Kürzen notwendig, dass die Terme faktorisiert vorliegen. Umgekehrt erleichtert es das Ableiten, wenn ein Term möglichst wenig Produkte enthält. Um zu erkennen, welche Umformungen möglich und sinnvoll sind, ist (leider) viel Übung nötig ...

Zum Abschluss

Warum sind Terme, die sich aus Potenzen, Wurzeln und Logarithmen zusammensetzen, so wichtig? Das liegt daran, dass sie uns allgemeingültige Beschreibungen von Zusammenhängen und damit umfassende, absolute Problemlösungen ermöglichen. Das ist nicht zuletzt eine Voraussetzung für den Computereinsatz zum Lösen mathematischer Probleme: Wir müssen den Computern ja die Vorgehensweisen für den Lösungsprozess "mitteilen" - und das geschieht über Terme. Etwas naheliegender ist der Gebrauch von Termen beim Lösen von Gleichungen. Auch hier muss man wissen, nach welchen Regeln - mathematisch korrekt - mit den Termen umgegangen werden muss, sonst würde man nicht die richtige Lösung ermitteln können. Ein letzter Grund, warum es sich lohnt, gewisse Fähigkeiten im Umgang mit Termen zu erwerben: Wer Terme sicher umformen kann, muss sich von bestimmten Formeln (z. B. von der Prozentformel) nur eine Form merken - und kann sich die restlichen Formen, wenn sie benötigt werden, herleiten.