Übersicht:

20.1 Geometrie - Aufgaben

1. Bemerkung vorab: Runden Sie bei den folgenden Aufgaben – wenn nötig – auf zwei Stellen nach dem Komma. Wichtig ist, immer erst ganz zum Schluss zu runden, damit die Rundungsfehler nicht zu groß werden!

2. Bemerkung vorab: Sofern in einer Aufgabe nicht anders vermerkt ist, beziehen sich die Punkt-, Längen- und Winkelbezeichnungen auf die Grafiken, die der Erklärungsseite dieses Kapitels hier bzw. hier zu finden sind.

1. Aufgabe

Berechnen Sie von folgenden Figuren Umfang und Flächeninhalt, soweit dies möglich ist!

1) Quadrat mit der Seitenlänge $a=69 \, mm$

2) Rechteck mit der Seitenlänge $a=230 \, cm$ und der Diagonalen $e=5 \, m$

3) Raute mit der Seitenlänge $c=4{,}5 \, cm$

4) Kreis mit dem Radius $r=2{,}5 \, cm$

5) Parallelogramm mit der Seitenlänge $a=33 \, cm$ und der Höhe $h_a=12 \, cm$

6) Rechtwinkliges Dreieck mit der Kathete $a=70 \, mm$ und der Kathete $b=4 \, cm$

7) Kreis mit dem Durchmesser $d=7{,}5 \, cm$

8) Trapez mit der Höhe $h=4 \, cm$ , den Seitenlängen $a=12 \, cm$ und $c=5 \, cm$

9) Rechtwinkliges Dreieck mit Höhe $h=5 \, m$ , Kathete $a=13 \, m$ und Hypotenusenabschnitt $q=\dfrac{25}{12} \, m$

10) Quadrat mit der Diagonalen $e=15{,}4 \, m$

11) Symmetrisches Trapez mit den Seitenlängen $a=25 \, cm$ , $b=11 \, cm$ und $c=18 \, cm$ sowie der Höhe $h=9{,}5 \, cm$

12) Raute mit der Seitenlänge $a=8 \, cm$ und der Diagonalen $e=13 \, cm$

2. Aufgabe

Berechnen Sie jeweils Umfang und Flächeninhalt des Drachenvierecks!

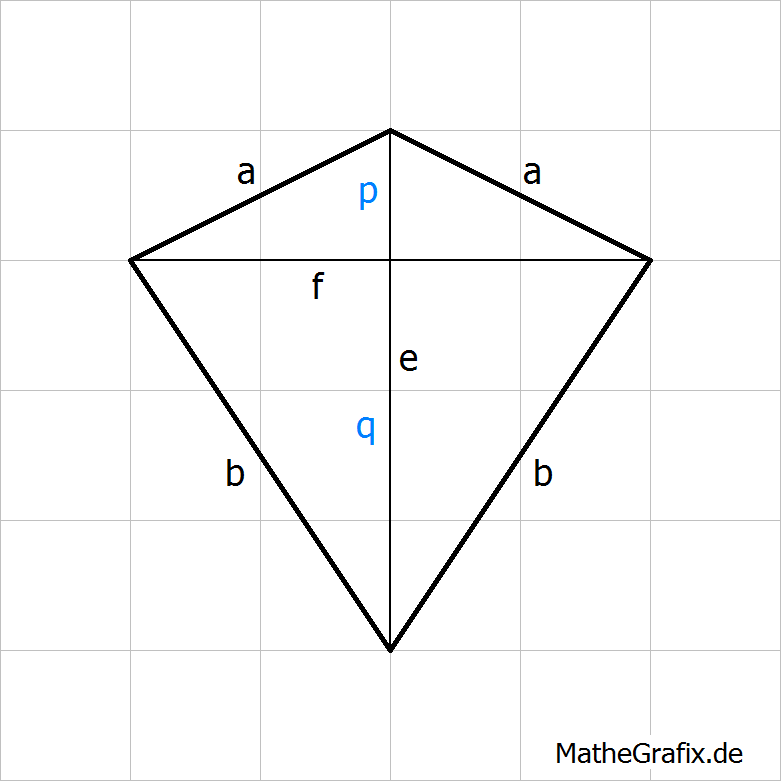
Drachenviereck mit zusätzlicher Beschriftung

1) $a=7{,}8 \,cm$ , $b=16 \, cm$ , $e=22{,}9 \, cm$ und $f=6 \, cm$

2) $a=2 \,cm$ , $e=7 \, cm$ und $p=1 \, cm$

3) $f=24 \,cm$ , $p=5 \, cm$ und $q=16 \, cm$

3. Aufgabe

Berechnen Sie jeweils die gesuchten Größen!

1) Umfang $U$ und Seitenlänge $b$ eines Rechtecks mit der Seitenlänge $a=3 \, cm$ und dem Flächeninhalt $A=27 \, cm^2$

2) Flächeninhalt $A$ und Seitenlänge $a$ eines Parallelogramms mit der Seitenlänge $b=5 \, cm$ , der Höhe $h_a=3 \, cm$ und dem Umfang $U=24 \,cm$

3) Umfang $U$ und Radius $r$ eines Kreises mit dem Flächeninhalt $A=37 \, cm^2$

4. Aufgabe

1) In einem Kreis $K_1$ sei der Radius $10 \, m$ lang. Wie groß ist der Radius eines Kreises mit doppeltem Flächeninhalt?

2) Ein Quadrat $Q_1$ habe einen Flächeninhalt von $16 \, cm^2$ . Wie lang sind die Seiten eines Quadrates mit halbem Flächeninhalt?

5. Aufgabe

Berechnen Sie aus den gegebenen Längen die fehlenden Dreiecksseiten, einschließlich der Hypotenusenabschnitte $p$ , $q$ und der Höhe $h$ !

1) Gegeben: Kathete $a=3 \, cm$ und Kathete $b=4 \, cm$

2) Gegeben: Hypotenusenabschnitt $p=5 \, cm$ und Höhe $h=5 \, cm$

3) Gegeben: Kathete $a=3{,}4\, cm$ und Hypotenuse $c=6{,}1\, cm$

4) Gegeben: Kathete $b=5{,}2\, cm$ und Hypotenusenabschnitt $q=1{,}2\, cm$

5) Gegeben: Hypotenuse $c=7 \, cm$ und Hypotenusenabschnitt $p=3{,}9\, cm$

6) Gegeben: Kathete $a=2{,}8\,mm$ , Hypotenusenabschnitt $p=1\,mm$

7) Gegeben: Kathete $a=16\,cm$ , Kathete $b=90\,mm$

8) Gegeben: Höhe $h=4{,}03\,m$ , Hypotenusenabschnitt $q=507\,cm$

9) Gegeben: Kathete $a=2{,}7183\,km$ , Hypotenuse $c=3{,}1416\,km$

10) Gegeben: Hypotenuse $c=5{,}34\,cm$ , Hypotenusenabschnitt $q=0{,}2\,cm$

11) Gegeben: Hypotenusenabschnitt $q=60{,}3\,cm$ , Kathete $b=603\,cm$

12) Gegeben: Hypotenusenabschnitte $p=0{,}3\,cm$ und $q=0{,}5\,cm$

13) Gegeben: Kathete $b=50\,cm$ , Kathete $a=0{,}5\,m$

14) Gegeben: Hypotenuse $c=753\,cm$ , Kathete $b=456\,cm$

15) Gegeben: Hypotenusenabschnitt $q=5\,m$ , Höhe $h=20\,m$

6. Aufgabe

Wie groß ist jeweils der Abstand $d$ der gegebenen Punkte $P_1$ und $P_2$ ?

1) $P_1 \left(1\mid 2 \right)$ und $P_2 \left(3\mid 3 \right)$		6) $P_1 \left(-0{,}5\mid 7{,}75 \right)$ und $P_2 \left(\dfrac{1}{2}\mid -\dfrac{31}{4} \right)$
2) $P_1 \left(\dfrac{1}{3} \mid 2 \right)$ und $P_2 \left(-\dfrac{2}{3}\mid 7 \right)$		7) $P_1 \left(0\mid 0 \right)$ und $P_2 \left(3\mid 4 \right)$
3) $P_1 \left(25\mid -50 \right)$ und $P_2 \left(-\dfrac{1}{10}\mid 2 \right)$		8) $P_1 \left(\dfrac{7}{8}\mid -\dfrac{9}{4} \right)$ und $P_2 \left(\dfrac{1}{4}\mid \dfrac{3}{8} \right)$
4) $P_1 \left(-\dfrac{1}{300}\mid \dfrac{3}{7}\right)$ und $P_2 \left(-\dfrac{11}{600}\mid -\dfrac{8}{21} \right)$		9) $P_1 \left(-90\mid -23 \right)$ und $P_2 \left(-83\mid -101 \right)$
5) $P_1 \left(7\mid 5 \right)$ und $P_2 \left(21\mid 22 \right)$		10) $P_1 \left(333\mid 111 \right)$ und $P_2 \left(33\mid 11 \right)$

7. Aufgabe

Kann es Dreiecke bzw. Vierecke geben, die die angegebenen Winkel enthalten?

Dreiecke		Vierecke
1) $\alpha = \dfrac{ \pi}{2}$ und $\beta = 100^\circ$		11) $\alpha = \dfrac{ 5\pi}{6}$ , $\beta = 30^\circ$ und $\gamma = 60^\circ$
2) $\alpha = 100^\circ$ und $\gamma = \dfrac{ \pi}{4}$		12) $\alpha = 45^\circ$ und $\beta = \dfrac{3\pi}{2}$ und $\gamma = \dfrac{\pi}{4}$
3) $\alpha = 120^\circ$ und $\beta= \dfrac{ \pi}{6}$		13) $\alpha = \dfrac{\pi}{9}$ und $\beta = 180^\circ$ und $\gamma = 10^\circ$
4) $\beta = \dfrac{3 \pi}{5}$ und $\gamma = 80^\circ$		14) $\alpha = \dfrac{9\pi}{8}$ und $\beta = 30^\circ$ und $\gamma = \dfrac{2\pi}{5}$
5) $\beta=\pi$ und $\gamma = 18^\circ$		15) $\alpha = \dfrac{11\pi}{18}$ und $\beta = 70^\circ$ und $\gamma = \dfrac{17\pi}{18}$
6) $\alpha=\dfrac{\pi}{10}$ und $\beta=145^\circ$		16) $\alpha = \dfrac{ 2\pi}{3}$ und $\beta = 30^\circ$ und $\gamma = \pi$
7) $\gamma =\dfrac{5\pi}{4}$ und $\beta=10^\circ$		17) $\alpha = 32^\circ$ und $\beta = \dfrac{6\pi}{5}$ und $\gamma = \dfrac{23\pi}{36}$
8) $\alpha = 30^\circ$ und $\beta=\dfrac{\pi}{3}$		18) $\alpha = 5^\circ$ und $\beta = 5^\circ$ und $\gamma = 0{,}1\pi$
9) $\alpha=\dfrac{3\pi}{8}$ und $\beta=45^\circ$		19) $\alpha = \dfrac{ \pi}{2}$ und $\beta = 120^\circ$ und $\gamma = 180^\circ$
10) $\alpha = 1{,}8^\circ$ und $\gamma=\dfrac{99}{100}\pi$		20) $\alpha = \dfrac{ 5\pi}{4}$ und $\beta = 90^\circ$ und $\gamma = \dfrac{5\pi}{12}$

8. Aufgabe

Familie Eckstein möchte eine rechteckige Steinterrasse bauen, wofür sie $1000\,\text{EUR}$ zur Seite gelegt hat. Für die Anfahrt des Steinsetzers muss sie einmalig $250\,\text{EUR}$ zahlen. Zusätzlich zahlt sie für jeden angefangenen Quadratmeter $60\,\text{EUR}$ . Eine Seitenlänge der Terrasse ist schon durch die Hauswand vorgegeben: $5\, m$ .

Wie groß kann die Terrasse maximal werden? Geben Sie die zweite Seitenlänge an!

9. Aufgabe

Berechnen Sie von folgenden Körpern Ober- und Mantelfläche sowie Volumen, soweit dies möglich ist!

1) Würfel mit der Seitenlänge $a=16 \, cm$

2) Quader mit den Seitenlängen $a =35 \, mm$ , $b=5{,}5 \, cm$ und $c=11 \, cm$

3) Zylinder mit der Höhe $h=10 \, m$ und dem Radius $r=7{,}5 \, m$

4) Regelmäßige quadratische Pyramide mit der Höhe $h=5 \, m$ und der Seitenlänge der Grundfläche $a=7 \, m$

5) Kegel mit der Höhe $h=31 \, cm$ und dem Radius $r=14 \, cm$

6) Kugel mit dem Durchmesser $d=6{,}7 \, cm$

10. Aufgabe

1) Die Diagonale eines Quadrats ist $5{,}657 \, cm$ lang. Wie lang sind die Seiten des Vierecks?

2) Die Raumdiagonale eines Würfels ist $17{,}321 \, cm$ lang. Wie lang sind die Kanten des Würfels?

3) Die Oberfläche einer Kugel ist $615{,}75 \, cm^2$ groß. Wie groß ist das Volumen der Kugel?

11. Aufgabe

1) In einem Quadrat mit der Seitenlänge $a$ ist ein Kreis mit maximalem Durchmesser eingezeichnet. Das heißt, der Kreis berührt die Quadratseiten von innen jeweils in der Mitte.
Wie ist das Verhältnis der Fläche des Kreises zur Fläche des Quadrates?

2) Zusätzlich ist um das Quadrat herum ein Kreis mit minimalem Durchmesser gezeichnet. Das heißt, das Quadrat berührt die Kreislinie von innen mit allen vier Ecken.
Wie ist das Verhältnis der Fläche dieses Kreises zur Fläche des Quadrates?

3) Formulieren Sie entsprechende Vergleiche im Raum. Anstelle von Quadraten sind damit Würfel zu betrachten, den Kreisen entsprechen Kugeln.
Wie ist das Verhältnis der entsprechenden Volumina?

12. Aufgabe

Das Dosenunternehmen "Dosen¹⁰" möchte weniger Material für seine $0{,}25\, l$ Dosen verwenden und dafür ggf. die Form ändern. Grundsätzlich wurden vier Ideen abgesegnet:

a) Ein Kreiszylinder mit einem Durchmesser von $7{,}5 \, cm$
b) Ein Quader, wobei eine Seite $4 \, cm$ breit sein soll und eine andere doppelt so lang wie diese
c) Ein Würfel
d) Eine Kugel

Welche Alternative ist optimal? Warum hat sich die rechnerisch optimale Lösung in der Praxis nicht durchgesetzt?

13. Aufgabe

Die Firma „Rohrfertigung nach Maß“ hat den Auftrag, Abwasserrohre herzustellen. Dabei soll der Gesamtdurchmesser des Rohres $200 \, mm$ sein, wobei der innere Durchmesser $150 \, mm$ ist. Die Länge des Rohres soll $15 \, m$ betragen.

a) Wie viel Abwasser kann das Rohr fassen?
b) Wie groß ist die Mantelfläche des Rohres?

14. Aufgabe

In einem Freizeitbad wurde ein neues Schwimmbecken gebaut mit Abmessungen, wie in der Skizze (Seitenansicht) dargestellt. Wie viele Liter Wasser werden benötigt, um den Pool bis $10\, cm$ unter den Rand zu füllen bei einem $15\, m$ breiten Becken?