Übersicht:

• Lösung zur 1. Aufgabe
• Lösung zur 2. Aufgabe
• Lösung zur 3. Aufgabe
• Lösung zur 4. Aufgabe
• Lösung zur 5. Aufgabe
• Lösung zur 6. Aufgabe
• Lösung zur 7. Aufgabe
• Lösung zur 8. Aufgabe
• Lösung zur 9. Aufgabe

6.3 Lineare Funktionen - Lösungen

1. Aufgabe

1)
$m = \dfrac{12-3}{2-(-1)} = \dfrac{9}{3} = 3$
Einsetzen von $m = 3$ und $A \left(2 \mid 12 \right)$ in die allgemeine Geradengleichung liefert: $12 = 3 \cdot 2 + n$ und damit $n = 6$
Also ist: $f_1(x) = 3x + 6$

2)
$m = \genfrac{}{}{1 pt}{0} {-1-4}{-1-\frac{3}{2}} = \genfrac{}{}{1 pt}{0} {-5}{-\frac{5}{2}} = 2$
Einsetzen von $m = 2$ und $A \left(-1 \mid -1 \right)$ in die allgemeine Geradengleichung liefert: $-1 = 2 \cdot (-1) + n$ und damit $n = 1$
Also ist: $f_2(x) = 2x + 1$

3)
$m = \dfrac{5-0}{0-10} = \dfrac{5}{-10} = -\dfrac{1}{2}$
Einsetzen von $m = -\dfrac{1}{2}$ und $P \left(0 \mid 5 \right)$ in die allgemeine Geradengleichung liefert: $5 = -\dfrac{1}{2} \cdot 0 + n$ und damit $n = 5$
Also ist: $f_3(x) = - \dfrac{1}{2}x + 5$

4)
$m = \genfrac{}{}{1 pt}{0} {\frac{1}{6}-\frac{1}{3}}{\frac{1}{2}-\frac{1}{3}} = \genfrac{}{}{1 pt}{0} {-\frac{1}{6}}{\frac{1}{6}} = -1$
Einsetzen von $m = -1$ und $Q \left( \dfrac{1}{3} \mid \dfrac{1}{3} \right)$ in die allgemeine Geradengleichung liefert: $\dfrac{1}{3} = -1 \cdot \dfrac{1}{3} + n$ und damit $n = \dfrac{2}{3}$
Also ist: $f_4(x) = -x + \dfrac{2}{3}$

5)
$m = \dfrac{8-(-3)}{3-2} = 11$
Einsetzen von $m = 11$ und $B \left(3 \mid 8 \right)$ in die allgemeine Geradengleichung liefert: $8 = 11 \cdot 3 + n$ und damit $n = -25$
Also ist: $f_5(x) = 11x - 25$

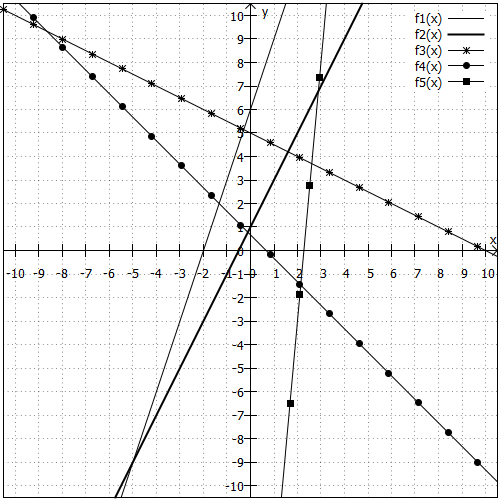
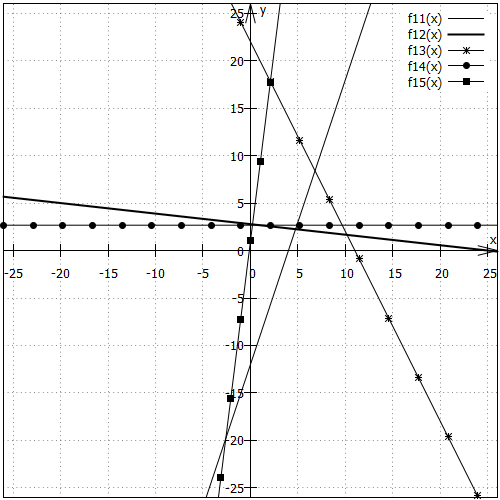
Diese Skaleneinteilung ist für $f_5(x)$ nicht ideal, weil ihr y-Achsenabschnitt außerhalb des gezeigten Bereichs liegt. Daher noch eine Grafik mit entsprechend angepassten Skalen:

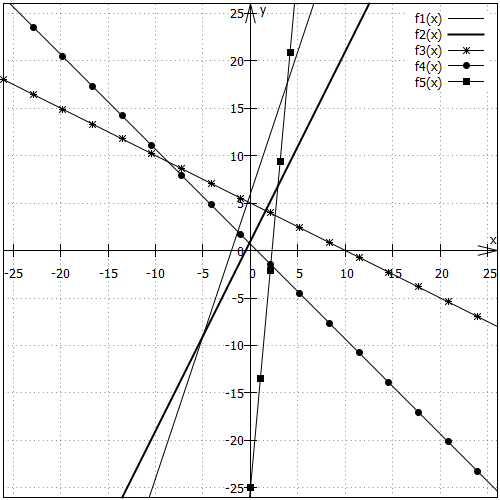
Diese Skaleneinteilung ist für die anderen Geraden nicht so geschickt, weil die Details aufgrund des großen Maßstabs verloren gehen. Daher haben beide Grafiken ihre Berechtigung.

6)
$m = \dfrac{-4-(-4)}{22-(-14)} = \dfrac{0}{36} = 0$ 
Einsetzen von $m=0$ und $R \left (22 \mid -4\right)$ in die allgemeine Geradengleichung liefert: $-4 = 0 \cdot 22 + n$ und damit $n= -4$
Also ist: $f_6(x) = -4$

7)
$m = \genfrac{}{}{1 pt}{0} {\frac{1}{4}- \left(-\frac{7}{2}\right)}{\frac{1}{2}-(-2)} = \genfrac{}{}{1 pt}{0} {\frac{15}{4}}{\frac{5}{2}} = \dfrac{3}{2}$
Einsetzen von $m=\dfrac{3}{2}$ und $L \left(-2 \mid -\dfrac {7}{2} \right)$ in die allgemeine Geradengleichung liefert: $-\dfrac{7}{2} = \dfrac{3}{2} \cdot (-2) + n$ und damit $n= -\dfrac{1}{2}$
Also ist: $f_7(x) = \dfrac{3}{2}x -\dfrac{1}{2}$

8)
$m = \genfrac{}{}{1 pt}{0} {\frac{7}{8}- \left(-\frac{1}{8} \right)}{3-(-1)} = \genfrac{}{}{1 pt}{0} {\frac{8}{8}}{4} = \dfrac{1}{4}$
Einsetzen von $m=\dfrac14$ und $B \left (-1 \mid -\dfrac18 \right )$ in die allgemeine Geradengleichung liefert: $-\dfrac18 = \dfrac14 \cdot (-1) + n$ und damit $n= \dfrac18$
Also ist: $f_8(x) = \dfrac{1}{4}x +\dfrac{1}{8}$

9)
$m = \genfrac{}{}{1 pt}{0} {-8-7}{\frac14 - (-1)} = \genfrac{}{}{1 pt}{0} {-15}{\frac{5}{4}} = -12$
Einsetzen von $m=-12$ und $P \left (\dfrac14 \mid -8 \right)$ in die allgemeine Geradengleichung liefert: $-8= -12 \cdot \dfrac14 + n$ und damit $n = -5$
Also ist: $f_9(x) = -12x -5$

10)
$m = \genfrac{}{}{1 pt}{0} {\frac{11}{6}-\left(-\frac16\right)}{-3-0}= \genfrac{}{}{1 pt}{0} {\frac{12}{6}}{-3} = -\dfrac{2}{3}$
Einsetzen von $m = -\dfrac{2}{3}$ und $H \left(0 \mid -\dfrac16 \right)$ in die allgemeine Geradengleichung liefert: $-\dfrac16 = -\dfrac{2}{3} \cdot 0 +n$ und damit $n = -\dfrac16$
Also ist: $f_{10}(x) = -\dfrac{2}{3}x - \dfrac16$

11)
$m = \dfrac{9-3}{7-5} = 3$
Einsetzen von $m=3$ und $A \left( 5 \mid 3 \right)$ in die allgemeine Geradengleichung liefert: $3 = 3 \cdot 5 + n$ und damit $n = -12$
Also ist: $f_{11}(x) = 3x - 12$

12)
$m = \dfrac{2-3}{7+2} = - \dfrac{1}{9} \approx 0{,}11$
Einsetzen von $m = -\dfrac{1}{9}$ und $B \left( 7 \mid 2 \right)$ in die allgemeine Geradengleichung liefert: $2 = -\dfrac{1}{9} \cdot 7 + n$ und damit $n = \dfrac{25}{9} \approx 2{,}78$
Also ist: $f_{12} (x) = -\dfrac{1}{9} x + \dfrac{25}{9}$

13)
$m = \dfrac{0-22}{11-0} = -2$
Einsetzen von $m = -2$ und $B \left( 11 \mid 0 \right)$ in die allgemeine Geradengleichung liefert: $0 = -2 \cdot 11 + n$ und damit $n = 22$
Also ist: $f_{13} (x) = -2x +22$

14)
$m = \genfrac{}{}{1 pt}{0} {\frac{8}{3} - \frac{8}{3}}{- \frac{7}{5} - \frac{19}{32}} = 0$
Einsetzen von $m = 0$ und $P \left( -\dfrac{7}{5} \mid \dfrac{8}{3} \right)$ in die allgemeine Geradengleichung liefert: $\dfrac{8}{3} = 0 \cdot \left( - \dfrac{7}{5} \right) + n$ und damit $n = \dfrac{8}{3}$
Also ist: $f_{14} (x) = \dfrac{8}{3} \approx 2{,}67$

15)
$m = \dfrac{9 + 55}{1+7} = 8$
Einsetzen von $m = 8$ und $S \left( 1 \mid 9 \right)$ in die allgemeine Geradengleichung liefert: $9 = 8 \cdot 1 + n$ und damit $n = 1$
Also ist: $f_{15} (x) = 8x +1$

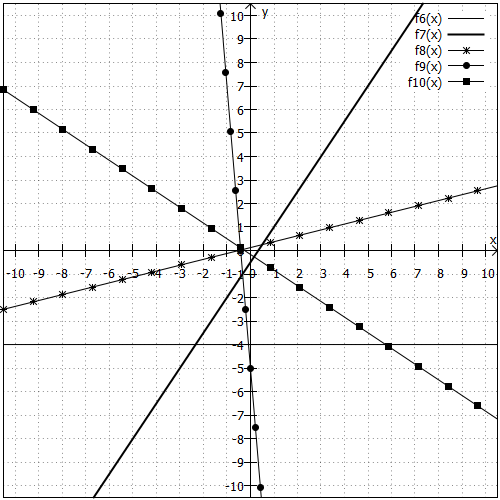
Diese Skaleneinteilung ist für $f_{11}(x)$ und $f_{13}(x)$ nicht ideal, weil ihr y-Achsenabschnitt außerhalb des gezeigten Bereichs liegt. Daher noch eine Grafik mit entsprechend angepassten Skalen:

16)
$m = \genfrac{}{}{1 pt}{0} {- \frac{24}{7} - 0}{-36-0} = \dfrac{2}{21} \approx 0{,}10$
Einsetzen von $m = \dfrac{2}{21}$ und $P \left( 0 \mid 0 \right)$ in die allgemeine Geradengleichung liefert: $0 = \dfrac{2}{21} \cdot 0 +n$ und damit $n = 0$
Also ist: $f_{16} (x) = \dfrac{2}{21} x$

17)
$m = \genfrac{}{}{1 pt}{0} {- \frac{7}{2}- \frac{1}{4}}{-5 - \frac{3}{2}} = \dfrac{15}{26} \approx 0{,}58$
Einsetzen von $m = \dfrac{15}{26}$ und $A \left( \dfrac{3}{2} \mid \dfrac{1}{4} \right)$ in die allgemeine Geradengleichung liefert: $\dfrac{1}{4} = \dfrac{15}{26} \cdot \dfrac{3}{2} + n$ und damit $n = - \dfrac{8}{13} \approx -0{,}62$
Also ist: $f_{17} (x) = \dfrac{15}{26} x - \dfrac{8}{13}$

18)
$m = \genfrac{}{}{1 pt}{0} {- \frac{1}{2} - \frac{3}{4}}{- \frac{5}{2} - \frac{15}{8}} = \dfrac{2}{7} \approx 0{,}29$
Einsetzen von $m = \dfrac{2}{7}$ und $P_1 \left( \dfrac{15}{8} \mid \dfrac{3}{4} \right)$ in die allgemeine Geradengleichung liefert: $\dfrac{3}{4} = \dfrac{2}{7} \cdot \dfrac{15}{8} + n$ und damit $n = \dfrac{3}{14} \approx 0{,}21$
Also ist: $f_{18} (x) = \dfrac{2}{7} x + \dfrac{3}{14}$

19)
$m = \genfrac{}{}{1 pt}{0} {\frac{53}{4} + \frac{17}{2}}{-19-17} = - \dfrac{29}{48} \approx -0{,}60$
Einsetzen von $m = - \dfrac{29}{48}$ und $D \left( -19 \mid \dfrac{53}{4} \right)$ in die allgemeine Geradengleichung liefert: $\dfrac{53}{4} = - \dfrac{29}{48} \cdot \left( -19 \right) + n$ und damit $n = \dfrac{85}{48} \approx 1{,}77$
Also ist: $f_{19} (x) = - \dfrac{29}{48} x + \dfrac{85}{48}$

20)
$m = \dfrac{-2-3}{100+25} = - \dfrac{1}{25} = -0{,}04$
Einsetzen von $m = - \dfrac{1}{25}$ und $P_1 \left( -25 \mid 3 \right)$ in die allgemeine Geradengleichung liefert: $3 = - \dfrac{1}{25} \cdot (-25) + n$ und damit $n = 2$
Also ist: $f_{20} (x) = - \dfrac{1}{25} x + 2$

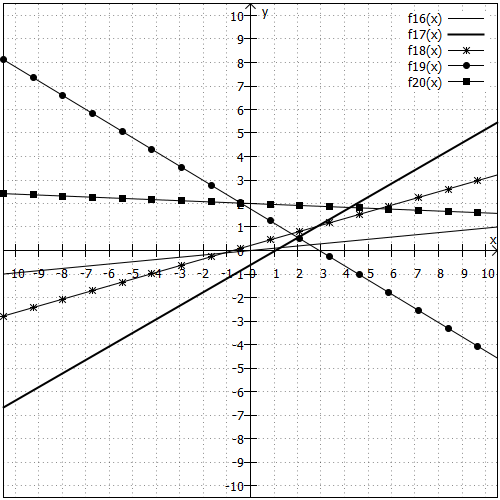
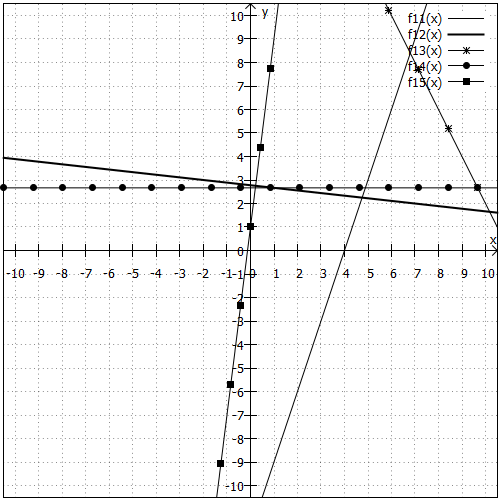
Diesmal ist die Skaleneinteilung nicht ideal, weil in der Nähe des Koordinatenursprungs "zu viel passiert" und die Grafik daher in diesem wichtigen Bereich nicht aufschlussreich ist. Daher noch eine Grafik mit entsprechend angepassten Skalen:

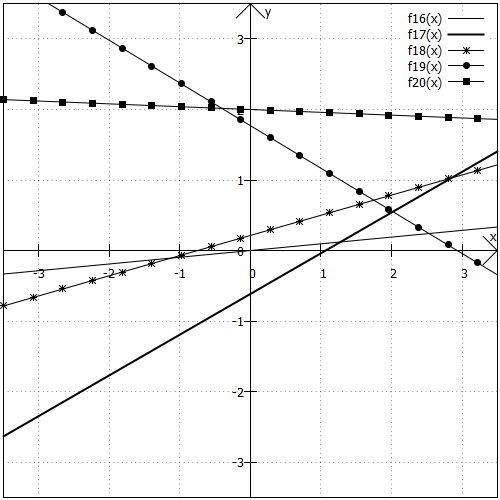
2. Aufgabe

Um festzustellen, ob ein Punkt auf einem Graphen liegt, muss der Funktionswert von $f(x)$ für den gegebenen x-Wert ausgerechnet werden und dieser mit dem gegebenen y-Wert verglichen werden.

1) $f(2)=15\cdot 2-6=24$
Der ausgerechnete Funktionswert stimmt mit dem gegebenen Wert überein. Der Punkt $P$ liegt also auf der Geraden $f(x)$.

2) $f(8)=0{,}4\cdot 8+6=9{,}2$
Der ausgerechnete Funktionswert stimmt nicht mit dem gegebenen Wert überein. Der Punkt $P$ liegt also nicht auf der Geraden $f(x)$.

3) $f(25)=-63\cdot 25+15=-1560$
Der ausgerechnete Funktionswert stimmt nicht mit dem gegebenen Wert überein. Der Punkt $P$ liegt also nicht auf der Geraden $f(x)$.

4) $f(14)=\dfrac{7}{8}\cdot 14=12{,}25$
Der ausgerechnete Funktionswert stimmt mit dem gegebenen Wert überein. Der Punkt $P$ liegt also auf der Geraden $f(x)$. 

5) $f(-6)=4\cdot \left(-6\right)+3=-21$
Der ausgerechnete Funktionswert stimmt mit dem gegebenen Wert überein. Der Punkt $P$ liegt also auf der Geraden $f(x)$.

6) $f(0{,}1)=-296\cdot 0{,}1=-29{,}6$
Der ausgerechnete Funktionswert stimmt nicht mit dem gegebenen Wert überein. Der Punkt $P$ liegt also nicht auf der Geraden $f(x)$.

7) $f(0)=288\cdot 0=0$
Der ausgerechnete Funktionswert stimmt mit dem gegebenen Wert überein. Der Punkt $P$ liegt also auf der Geraden $f(x)$.

8) $f(14)=-347\cdot 14-101=-4.959$
Der ausgerechnete Funktionswert stimmt mit dem gegebenen Wert überein. Der Punkt $P$ liegt also auf der Geraden $f(x)$.

9) $f(7)=11\cdot 7+24=101$
Der ausgerechnete Funktionswert stimmt nicht mit dem gegebenen Wert überein. Der Punkt $P$ liegt also nicht auf der Geraden $f(x)$.

10) $f(22)=\dfrac{12}{11}\cdot 22-\dfrac{1}{9}\approx23{,}89$
Der ausgerechnete Funktionswert stimmt nicht mit dem gegebenen Wert überein. Der Punkt $P$ liegt also nicht auf der Geraden $f(x)$.

3. Aufgabe

1) Der Graph von $f(x)$ ist konstant, da $m=0$, und schneidet die y-Achse bei einer negativen Zahl, da $n < 0$.

2) Der Graph von $f(x)$ steigt, da $m>0$, und schneidet die y-Achse bei einer negativen Zahl, da $n < 0$.

3) Der Graph von $f(b)$ fällt, da $m < 0$, und schneidet die y-Achse bei einer positiven Zahl, da $n > 0$.

4) Der Graph von $f(a)$ steigt, da $m>0$, und schneidet die y-Achse bei einer negativen Zahl, da $n < 0$.

5) Der Graph von $g(x)$ fällt, da $m < 0$, und schneidet die y-Achse bei einer positiven Zahl, da $n > 0$.

6) Der Graph von $f(x)$ steigt, da $m>0$, und schneidet die y-Achse bei $0$.

7) Der Graph von $f(x)$ ist konstant, da $m=0$, und schneidet die y-Achse bei einer negativen Zahl, da $n < 0$.

Bemerkung: Da die Funktion $f(x)$ heißt, wissen wir, dass die Variable $x$ ist und nicht $a$, wie man denken könnte. $a\in\mathbb{R}^-$ ist eine negative Konstante.

8) Der Graph von $f(z)$ fällt, da $m < 0$, und schneidet die y-Achse bei $0$.

Bemerkung: Man muss $(-754)^{39}$ nicht ausrechnen, um die Frage nach dem Schnittpunkt mit der y-Achse beantworten zu können. Es reicht festzustellen, dass hier eine negative Basis mit einem ungeraden Exponenten potenziert wird. Da "minus mal minus gleich plus" ist, hebt sich eine gerade Anzahl an Minuszeichen auf. Ein Minuszeichen bleibt quasi übrig. Das Ergebnis ist also negativ.

9) Der Graph von $v(x)$ steigt, da $m>0$, und schneidet die -Achse bei einer negativen Zahl, da $n < 0$.

10) Der Graph von $u(x)$ fällt, da $m < 0$, und schneidet die y-Achse bei einer positiven Zahl, da $n>0$.

4. Aufgabe

Schnittpunkt mit der x-Achse $S_x$: Beim Schnittpunkt eines Graphen mit der x-Achse muss die y-Koordinate $0$ sein. Wäre die y-Koordinate ungleich $0$, würde der Punkt ober- oder unterhalb der x-Achse liegen. Der Funktionsterm, der ja für die y-Koordinate steht, muss also nullgesetzt werden. Die Lösung der entstehenden lineare Gleichung ist die gesuchte Koordinate.

Schnittpunkt mit der y-Achse $S_y$: Bei linearen Funktionen ist es einfach, den Schnittpunkt des Graphen mit der y-Achse zu bestimmen. Der y-Achsenabschnitt ist ja definiert als Schnittpunkt des Graphen mit der y-Achse, sodass die gesuchte Koordinate direkt abgelesen werden kann. Die x-Koordinate dieses Schnittpunkts ist $0$. Bei komplizierteren Funktionen müsste $x=0$ in den Funktionsterm eingesetzt und das Ergebnis ausgerechnet werden.

1)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} 24x-6 &=& 0 &\vert & +6 \cr 24x &=& 6 &\vert& : 24 \cr x &=& \dfrac{1}{4} \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_x \left(\dfrac{1}{4} \mid 0\right)$.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid -6\right)$.

2)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} \dfrac{4}{3}x-2 &=& 0 &\vert& +2 \cr \dfrac{4}{3}x &=& 2 &\vert& \cdot \dfrac{3}{4} \cr x &=& \dfrac{6}{4} \cr\cr x &=& \dfrac{3}{2} \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_x \left(\dfrac{3}{2} \mid 0\right)$.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid -2\right)$.

3)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} -6x+8 &=& 0 &\vert& -8 \cr -6x &=& -8 &\vert& :(-6) \cr x &=& \dfrac{8}{6} \cr\cr x &=& \dfrac{4}{3} \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_x \left(\dfrac{4}{3} \mid 0\right)$.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid 8\right)$.

4)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} x+48 &=& 0 &\vert& -48 \cr x &=& -48 \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_x \left(-48 \mid 0\right)$.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid 48\right)$.

5)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} 15x-11 &=& 0 &\vert& +11 \cr 15x &=& 11 &\vert& :15 \cr x &=& \dfrac{11}{15} \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_x \left(\dfrac{11}{15} \mid 0\right)$.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid -11\right)$.

6)
Schnittpunkt mit der x-Achse: 
$\begin{array}{rclcl} \dfrac{5}{4}x+41 &=& 0 &\vert& -41 \cr \dfrac{5}{4}x &=& -41 &\vert& \cdot \dfrac{4}{5} \cr x &=& -\dfrac{164}{5} \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_x \left(-\dfrac{164}{5} \mid 0\right)$.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid 41\right)$.

7)
Schnittpunkt mit der x-Achse: 
$\begin{array}{rclcl} \dfrac{6}{7} x-10 &=& 0 &\vert&+10 \cr \dfrac{6}{7}x &=& 10 &\vert& \cdot \dfrac{7}{6} \cr x &=& \dfrac{70}{6} \cr\cr x &=& \dfrac{35}{3} \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_x \left(\dfrac{35}{3} \mid 0\right)$.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid -10\right)$.

8)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} -12x &=& 0 &\vert& :(-12) \cr x &=& 0 \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_x \left(0 \mid 0\right)$.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid 0\right)$.

9)
Schnittpunkt mit der x-Achse:
$\begin{array}{rclcl} -\dfrac{3}{2}x-2 &=& 0 &\vert& +2 \cr -\dfrac{3}{2}x &=& 2 &\vert& \cdot \left(-\dfrac{2}{3}\right) \cr x &=& -\dfrac{4}{3} \end{array}$

Der Schnittpunkt mit der x-Achse ist also $S_x \left(-\dfrac{4}{3} \mid 0\right)$.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid -2\right)$.

10)
Schnittpunkt mit der x-Achse: 
$\begin{array}{rclcl} -23 &=& 0 \end{array}$

Diese Gleichung hat keine Lösung. $S_x$ existiert also nicht. Grafisch erkennt man dies daran, dass die Gerade horizontal verläuft. Daher schneidet sie die x-Achse nicht.

Der Schnittpunkt mit der y-Achse ist $S_y \left(0\mid -23\right)$.

5. Aufgabe

1)
a)
$\begin{array}{rclll} f(2{,}5) &=& 3 \cdot 2{,}5+5 &=& 12{,}5 \quad \rightarrow \quad P_1(2{,}5 \mid 12{,}5) \end{array}$

b)
$\begin{array}{rclll} 26 &=& 3x+5 &\vert & -5 \cr21 &=& 3x &\vert & :3 \cr7 &=& x & & \rightarrow \quad P_2(7 \mid 26) \end{array}$

2)
a)
$\begin{array}{rclll} f(31) &=& -31-\dfrac{1}{2} &=& -31{,}5 \quad \rightarrow \quad P_1(31 \mid -31{,}5) \end{array}$

b)
$\begin{array}{rclll} 7{,}5 &=& -x-\dfrac{1}{2} & \vert & +\dfrac{1}{2} \cr8 &=& -x & \vert & \cdot (-1) \cr-8 &=& x && \rightarrow \quad P_2(-8 \mid 7{,}5) \end{array}$

3)
a)
$\begin{array}{rclll} f(2) &=& -4{,}5 \cdot 2+37 &=& 28 \quad \rightarrow \quad P_1(2 \mid 28) \end{array}$

b)
$\begin{array}{rclll} 130 &=& -4{,}5x+37 &\vert & -37 \cr93 &=& -4{,}5x &\vert & :(-4{,}5) \cr-\dfrac{62}{3} &=& x && \rightarrow \quad P_2\left(-\dfrac{62}{3} \mid 130\right) \end{array}$

4)
a)
$\begin{array}{rclll} f(-5) &=& \dfrac{3}{2} \cdot (-5)-24 &=& -31{,}5 \quad \rightarrow \quad P_1(-5 \mid -31{,}5) \end{array}$

b)
$\begin{array}{rclll} -20 &=& \dfrac{3}{2}x-24 &\vert & +24 \cr4 &=& \dfrac{3}{2}x &\vert & : \dfrac{3}{2} \cr\dfrac{8}{3} &=& x && \rightarrow \quad P_2\left(\dfrac{8}{3} \mid -20\right) \end{array}$

5)
a)
$\begin{array}{rclll} f(2) &=& \dfrac{2}{3} \cdot 2-\dfrac{5}{4} &=& \dfrac{1}{12} \quad \rightarrow \quad P_1\left(2 \mid \dfrac{1}{12}\right) \end{array}$

b)
$\begin{array}{rclll} \dfrac{19}{12} &=& \dfrac{2}{3}x-\dfrac{5}{4} &\vert & +\dfrac{5}{4} \cr\dfrac{17}{6} &=& \dfrac{2}{3}x &\vert & : \dfrac{2}{3} \cr\dfrac{17}{4} &=& x && \rightarrow \quad P_2\left(\dfrac{17}{4} \mid \dfrac{19}{12}\right) \end{array}$

6)
a)
$\begin{array}{rclll} f(5) &=& -13 \cdot 5 &=& -65 \quad \rightarrow \quad P_1(5 \mid -65) \end{array}$

b)
$\begin{array}{rclll} -104 &=& -13x &\vert & :(-13) \cr8 &=& x && \rightarrow \quad P_2(8 \mid -104) \end{array}$

7)
a)
$\begin{array}{rclll} f\left(\dfrac{3}{4}\right) &=& -3 \cdot \dfrac{3}{4}+\dfrac{5}{4} &=& -1 \quad \rightarrow \quad P_1\left(\dfrac{3}{4} \mid -1\right) \end{array}$

b)
$\begin{array}{rclll} -16 &=& -3x+\dfrac{5}{4} &\vert & -\dfrac{5}{4} \cr-\dfrac{69}{4} &=& -3x &\vert & :(-3) \cr\dfrac{23}{4} &=& x && \rightarrow \quad P_2\left(\dfrac{23}{4} \mid -16\right) \end{array}$

8)
a)
$\begin{array}{rclll} f(18) &=& \dfrac{1}{20} \cdot 18+20 &=& 20{,}9 \quad \rightarrow \quad P_1(18 \mid 20{,}9) \end{array}$

b)
$\begin{array}{rclll} 20{,}45 &=& \dfrac{1}{20}x+20 &\vert & -20 \cr0{,}45 &=& \dfrac{1}{20}x &\vert & \cdot 20 \cr9 &=& x && \rightarrow \quad P_2(9 \mid 20{,}45) \end{array}$

9)
a)
$\begin{array}{rclll} f(11) &=& -\dfrac{2}{5} \cdot 11+1 &=& -3{,}4 \quad \rightarrow \quad P_1(11 \mid -3{,}4) \end{array}$

b)
$\begin{array}{rclll} 0 &=& -\dfrac{2}{5}x+1 &\vert & -1 \cr-1 &=& -\dfrac{2}{5}x &\vert & : \left(-\dfrac{2}{5}\right) \cr\dfrac{5}{2} &=& x && \rightarrow \quad P_2\left(\dfrac{5}{2} \mid 0\right) \end{array}$

10)
a)
$\begin{array}{rclll} f\left(-\dfrac{2}{5}\right) &=& -12 \cdot -\dfrac{2}{5}+\dfrac{11}{5} &=& 7 \quad \rightarrow \quad P_1\left(-\dfrac{2}{5} \mid 7\right) \end{array}$

b)
$\begin{array}{rclll} 4{,}2 &=& -12x+\dfrac{11}{5} &\vert & -\dfrac{11}{5} \cr2 &=& -12x &\vert & :(-12) \cr-\dfrac{1}{6} &=& x && \rightarrow \quad P_2\left(-\dfrac{1}{6} \mid 4{,}2\right) \end{array}$

6. Aufgabe

Lagebeziehung von $f_1(x)$ und $f_2(x)$
Wir prüfen zuerst, ob die Funktionen $f_1(x)$ und $f_2(x)$ die gleiche Steigung haben: $m_1=3$ und $m_2=-7$. Da die Steigungen offensichtlich unterschiedlich sind, können die Geraden weder parallel noch identisch sein. Sie müssen also einen Schnittpunkt, nennen wir ihn $S(x_s \mid y_s)$, haben.

x-Wert vom Schnittpunkt berechnen:
$\begin{array}{rclcl} f_1(x_s) &=& f_2(x_s) \cr 3x_s-6 &=& -7x_s-6 &\vert & +6 \cr 3x_s &=& -7x_s &\vert & +7x_s \cr 10x_s &=& 0 &\vert & :10 \cr x_s &=& 0\end{array}$

y-Wert vom Schnittpunkt berechnen:
$\begin{array}{rcl} f_1(x_s) &=& f_1(0) \cr &=& 3 \cdot 0 -6 \cr &=& -6 \end{array}$

Die Koordinaten des Schnittpunkts sind $S (0 \mid -6)$. Zur Überprüfung kann man den y-Wert mit $f_2(x)$ noch einmal berechnen (und dabei hoffentlich das gleiche Ergebnis erhalten) oder eine Punktprobe durchführen.

Bemerkung: Wer in diesem Fall direkt sieht, dass beide Geraden den gleichen y-Achsenabschnitt haben, darf den Schnittpunkt auch einfach ablesen ... Mehr als diesen einen kann es hier ja nicht geben.

Lagebeziehung von $f_1(x)$ und $f_3(x)$
Wir prüfen zuerst, ob $f_1(x)$ und $f_3(x)$ die gleiche Steigung haben: $m_1=3$ und $m_3=\frac{27}{9}=3$. Da die Steigungen gleich sind, können die Geraden parallel oder identisch sein. Einen einzelnen Schnittpunkt können sie nicht haben.

Zu prüfen ist jetzt, ob die Geraden parallel oder identisch sind. Dazu vergleichen wir die Schnittpunkte mit der y-Achse: $n_1=-6$ und $n_3=1$. Die beiden Geraden schneiden die y-Achse an unterschiedlichen Punkten. Sie sind somit nicht identisch, sondern verlaufen parallel.

Lagebeziehung von $f_1(x)$ und $f_4(x)$
Wir prüfen zuerst, ob $f_1(x)$ und $f_4(x)$ die gleiche Steigung haben: $m_1=3$ und $m_4=-\frac{21}{3}=-7$. Da die Steigungen offensichtlich unterschiedlich sind, können die Geraden weder parallel noch identisch sein. Sie müssen also einen Schnittpunkt, nennen wir ihn $S(x_s \mid y_s)$, haben.

An den Geradengleichungen kann man ablesen, dass $n_1=-6$ und $n_4=-6$ ist. Beide Geraden schneiden die y-Achse bei $-6$. Damit hat der Schnittpunkt der Funktionen $f_1(x)$ und $f_4(x)$ die Koordinaten $S (0 \mid -6)$.

Lagebeziehung von $f_2(x)$ und $f_3(x)$
Zunächst prüfen wir wieder, ob die Funktionen $f_2(x)$ und $f_3(x)$ die gleiche Steigung haben: $m_2=-7$ und $m_3=\frac{27}{9}=3$. Da die Steigungen offensichtlich unterschiedlich sind, können die Geraden weder parallel noch identisch sein. Sie müssen also einen Schnittpunkt $S(x_s \mid y_s)$ haben.

x-Wert vom Schnittpunkt berechnen:
$\begin{array}{rclcl} f_2(x_s) &=& f_3(x_s) \cr -7x_s-6 &=& \dfrac{27}{9}x_s+1 \cr -7x_s-6 &=& 3x_s+1 &\vert & +6 \cr -7x_s &=& 3x_s+7 &\vert & -3x_s \cr -10x_s &=& 7 &\vert & :(-10) \cr x_s &=& -\dfrac{7}{10}\end{array}$

y-Wert vom Schnittpunkt berechnen:
$\begin{array}{rcl} f_2(x_s) &=& f_2\left(-\dfrac{7}{10}\right) \cr &=& -7 \cdot \left(-\dfrac{7}{10}\right) -6 \cr &=& -\dfrac{11}{10} \end{array}$

Die Koordinaten des Schnittpunkts sind $S \left(-\dfrac{7}{10} \mid -\dfrac{11}{10}\right)$.

Lagebeziehung von $f_2(x)$ und $f_4(x)$
Wir prüfen zuerst, ob $f_2(x)$ und $f_4(x)$ die gleiche Steigung haben: $m_2=-7$ und $m_4=-\frac{21}{3}=-7$. Da die Steigungen gleich sind, können die Geraden parallel oder identisch sein. Einen einzelnen Schnittpunkt können sie nicht haben.

Um zu prüfen, ob die Geraden parallel oder identisch sind, lesen wir den jeweiligen Schnittpunkt mit der y-Achse ab: $n_2=-6$ und $n_4=-\frac{24}{4}=-6$. Die beiden Geraden schneiden die y-Achse im selben Punkt. Sie sind also identisch.

Lagebeziehung von $f_3(x)$ und $f_4(x)$
Wir prüfen wieder zuerst, ob $f_3(x)$ und $f_4(x)$ die gleiche Steigung haben: $m_3=\frac{27}{9}=3$ und $m_4=-\frac{21}{3}=-7$. Anhand der unterschiedlichen Steigungen ist zu erkennen, dass die Geraden weder parallel noch identisch sein können. Sie werden also einen Schnittpunkt $S(x_s \mid y_s)$ haben.

x-Wert vom Schnittpunkt berechnen:
$\begin{array}{rclcl} f_3(x_s) &=& f_4(x_s) \cr\dfrac{27}{9}x_s+1 &=& -\dfrac{21}{3}x_s-\dfrac{24}{4} \cr 3x_s+1 &=& -7x_s-6 &\vert & -1 \cr 3x_s &=& -7x_s-7 &\vert & +7x_s \cr 10x_s &=& -7 &\vert & :10 \cr x_s &=& -\dfrac{7}{10} \end{array}$

y-Wert vom Schnittpunkt berechnen:
$\begin{array}{rcl} f_3(x_s) &=& f_3\left(-\dfrac{7}{10}\right) \cr &=&\dfrac{27}{9} \cdot \left(-\dfrac{7}{10} \right)+1 \cr &=&3\cdot\left(-\dfrac{7}{10} \right)+\dfrac{10}{10}\cr &=&-\dfrac{11}{10}\end{array}$

Die Koordinaten des Schnittpunkts sind $S \left(-\dfrac{7}{10} \mid -\dfrac{11}{10}\right)$.

Bemerkung: Wer die Idee hatte, die Brüche in der Funktion vor dem Berechnen zu kürzen, ist vermutlich schneller zu diesem Ergebnis gekommen: $f_4(x)=-\dfrac{21}{3}x-\dfrac{24}{4}=-7x-6$. Diese Funktion kennen wir schon als $f_2(x)$ ...

7. Aufgabe

$f_1(x) = -4x+0 = -4x$
Begründung:
Der Schnittpunkt mit der y-Achse liegt direkt im Nullpunkt, also bei $0$.
Die Änderung des y-Wertes im Verhältnis zum x-Wert ist hier $\dfrac{-4}{1}$. Die Steigung ist also $-4$.
 
$f_2(x) = 5x+2$
Begründung:
Der Schnittpunkt mit der y-Achse liegt bei $2$.
Die Änderung des y-Wertes im Verhältnis zum x-Wert ist hier $\dfrac{5}{1}$. Die Steigung ist also $5$.
 
$f_3(x) = \dfrac{1}{4}x-3$
Begründung:
Der Schnittpunkt mit der y-Achse liegt bei $-3$.
Die Änderung des y-Wertes im Verhältnis zum x-Wert ist hier $\dfrac{1}{4}$. Die Steigung ist also $\dfrac{1}{4}$.
 
$f_4(x) = 0x+ 7 = 7$
Begründung:
Der Schnittpunkt mit der y-Achse liegt bei $7$.
Die Änderung des y-Wertes im Verhältnis zum x-Wert ist hier $\dfrac{0}{0}$. Die Steigung ist also $0$.
 
$f_5(x) = -2x-6$
Begründung:
Der Schnittpunkt mit der y-Achse liegt $-6$.
Die Änderung des y-Wertes im Verhältnis zum x-Wert ist hier $\dfrac{-2}{1}$. Die Steigung ist also $-2$.

8. Aufgabe

Sei $L$ die Länge der Kerzen zum Zeitpunkt $0$. Die Zeit ist dabei die unabhängige Variable und wird auf der x-Achse eingetragen. Die Länge der Kerze, die ja von der (Brenn-)Zeit abhängt, ist die abhängige Variable und wird auf der y-Achse eingetragen. Mathematisch kann man die erste Aussage daher als Punkt $P(0 \mid L)$ notieren.

Für die erste Kerze kennen wir also den Punkt $P_1(0 \mid L)$. Außerdem wissen wir, dass sie nach $8$ Stunden die Länge $0$ hat, was wir als Punkt $Q_1(8 \mid 0)$ notieren können.

Für die zweite Kerze kennen wir ebenfalls den Punkt $P_2(0 \mid L)$ und außerdem $Q_2(4 \mid 0)$, weil sie nach $4$ Stunden die Länge $0$ hat.

Zeichnet man für jede Kerze die beiden Punkte in ein Koordinatensystem und verbindet sie, ergibt sich folgende Grafik (Bitte beachten Sie, dass die Längen-Achse keine Einheiten hat - diese ist ja in der Aufgabe nicht gegeben!):

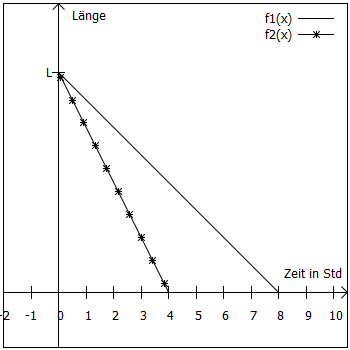
Daraus kann man nun lineare Funktionen $f(x) = mx + n$ berechnen:

$f_1(x)$:
Steigung: $m=\dfrac{\Delta y}{\Delta x} = \dfrac{0-L}{8-0} = -\dfrac{L}{8}$

y-Achsenabschnitt: $n = L$ (Das sieht man z. B. in der Grafik.)

$\Rightarrow f_1(x) = -\dfrac{L}{8}x+L =\left(-\dfrac{1}{8}x+1\right)L$

$f_2(x)$:

Steigung: $m=\dfrac{\Delta y}{\Delta x} = \dfrac{0-L}{4-0} = -\dfrac{L}{4}$

y-Achsenabschnitt: $n = L$ (Kann man ebenfalls in der Grafik ablesen.)

$\Rightarrow f_2(x) = -\dfrac{L}{4}x+L =\left(-\dfrac{1}{4}x+1\right)L$

Gesucht ist nun der Zeitpunkt $x_0$, an dem die erste Kerze doppelt so lang ist wie die zweite. Anders gesagt: "$2$ mal die Länge der zweiten Kerze" ist genauso groß wie die Länge der ersten Kerze.

Mathematisch schreibt man:

$\begin{array}{rclll} 2\left(-\dfrac{1}{4}x_0+1\right)L &=& \left(-\dfrac{1}{8}x_0+1\right)L &\vert& :L \cr\cr 2\left(-\dfrac{1}{4}x_0+1\right) &=& -\dfrac{1}{8}x_0+1 \cr\cr -\dfrac{1}{2}x_0+2 &=& -\dfrac{1}{8}x_0+1 &\vert& +\dfrac{1}{8}x_0-2 \cr\cr-\dfrac{3}{8}x_0 &=& -1 &\vert& :\left(-\dfrac{3}{8}\right) \cr\cr x_0 &=& \dfrac{8}{3}\end{array}$

Nach $\frac{8}{3}$ Stunden ist also die erste Kerze doppelt so lang ist wie die zweite. Das könnte man grundsätzlich so stehen lassen, meist würde man aber eher umrechnen und sagen: Nach $2$ Stunden und $40$ Minuten ist die erste Kerze doppelt so lang wie die zweite.

9. Aufgabe

Im dreidimensionalen Raum gibt es zunächst mal die gleichen Lagebeziehungen wie im zweidimensionalen: Die Geraden können parallel zueinander sein, sie können aufeinander liegen und sie können einen Schnittpunkt haben. Da eine Ebene ja Teil des dreidimensionalen Raumes ist, kann sich an diesen Möglichkeiten gar nichts ändern.

Durch die zusätzliche Dimension wird aber eine weitere Lagebeziehung möglich: Hier ist es möglich, dass zwei nicht parallele Geraden keine gemeinsamen Punkte haben. Dies wird als windschief bezeichnet.
Ein (leicht idealisiertes ...) Beispiel aus dem Alltag: Stellen Sie sich zwei schnurgerade Straßen vor. Die eine verbindet Berlin und Köln miteinander, die andere Hamburg und München. Verliefen beide auf dem Erdboden (also annähernd zweidimensional) gäbe es irgendwo in der Mitte Deutschlands eine Kreuzung; mathematisch gesehen wäre dies ein Schnittpunkt. Im Dreidimensionalen kann man sich vorstellen, dass die eine Straße auf einer Brücke in $10 \,\text{m}$ Höhe verläuft. Nun "schneiden" sich die Straßen nicht mehr; sie verlaufen aneinander vorbei. Da sie auch nicht parallel sind (sie verlaufen ja offensichtlich in unterschiedlichen Richtungen), sind sie also windschief.