Dieses Kapitel enthält die folgenden Themen:

• Ungleichungen allgemein
• Lineare Ungleichungen
• Quadratische Ungleichungen
• Bruchungleichungen

11.2 Ungleichungen - Erklärungen

In Kapitel 5 hatten wir Gleichungen eingeführt als "ein Term = ein (anderer) Term". Ganz ähnlich funktioniert es für Ungleichungen. Allerdings gibt es hier vier Varianten:

• "ein Term $<$ ein (anderer) Term"
• "ein Term $\leq$ ein (anderer) Term"
• "ein Term $>$ ein (anderer) Term"
• "ein Term $\geq$ ein (anderer) Term"

Die Vergleichszeichen oder auch Relationszeichen heißen:

• Kleinerzeichen: $<$ (gesprochen: "kleiner als", manchmal auch "echt kleiner als")
• Kleinergleichzeichen: $\leq$ (gesprochen: "kleiner gleich")
• Größerzeichen: $>$ (gesprochen: "größer als", manchmal auch "echt größer als")
• Größergleichzeichen: $\geq$ (gesprochen: "größer gleich")

Merke: Die Vergleichszeichen sind immer zur größeren Seite geöffnet.

Auch "ein Term $\neq$ ein (anderer) Term" (mit dem Ungleichheitszeichen $\neq$) ist natürlich eine Ungleichung. Allerdings brauchen wir sie nicht gesondert zu behandeln, weil man ja "nur" die zugehörige Gleichung lösen muss. Alles, was dabei nicht Lösung ist, ist dann Lösung der Ungleichung.


Wie bei Gleichungen ist es auch bei Ungleichungen meist die Aufgabe, diejenigen Werte der Variablen zu ermitteln, für die die Ungleichung wahr wird. Anders formuliert: Man möchte die Lösungen der Ungleichungen finden. Grundsätzlich behandelt man Ungleichungen genauso wie Gleichungen, nämlich mit Äquivalenzumformungen. Beispielsweise müssen (natürlich!) auch bei Ungleichungen alle Umformungen auf beiden Seiten durchgeführt werden, damit sich die Lösungsmenge nicht ändert. Ein paar Unterschiede gibt es allerdings schon zu beachten. Die grundlegendsten Unterschiede sind:

• Vertauscht man die beiden Seiten einer Ungleichung, muss auch das Vergleichszeichen "umgedreht" werden.
  Beispiel: Aus $4>2$ wird naheliegenderweise $2 < 4$.
  
  
• Bei Multiplikation mit negativen Zahlen muss das Vergleichszeichen ebenfalls "umgedreht" werden. Dies schließt die Division mit ein.
  Beispiel: Aus $4>2$ wird $-4 < -2$.

Diese Regeln gelten natürlich auch für die anderen Vergleichszeichen und wenn Variablen etc. in der Ungleichung enthalten sind. Bei Ungleichungen mit Variablen ist allerdings meist nicht mehr ganz so offensichtlich wie hier, wie man vorgehen muss ... In vielen Fällen kommt man ohne eine sogenannte Fallunterscheidung nicht aus. Fallunterscheidungen sind grundsätzlich nichts Geheimnisvolles oder Schlimmes. Sie sind dazu da, verschiedene Fälle, in denen unterschiedlich weiter gerechnet oder argumentiert werden muss, voneinander zu trennen. Vergisst man das, entstehen üblicherweise Fehler, weil man zu viele Dinge über einen Kamm schert. Multipliziert man beispielsweise eine Ungleichung mit der Variablen $x\in\mathbb{R}$, kann man nicht wissen, ob das Vergleichszeichen "umgedreht" werden muss oder nicht, weil man ja nicht weiß, ob $x$ positiv oder negativ ist. Es ist ja das Wesen von Variablen, dass wir eben im Vorhinein nicht wissen, für welchen Zahlenwert sie stehen. Es könnte sogar sein, dass die Multiplikation als Äquivalenzumformung überhaupt nicht zulässig ist, nämlich wenn $x=0$ gilt.
Beispiel: Multipliziert man die Ungleichung $4>2$ mit $x$, können wir nicht entscheiden, ob die neue Ungleichung $4x>2x$ lauten muss oder $4x < 2x$. Bei $x>0$ wäre die erste Ungleichung richtig, bei $x < 0$ die zweite. Dass die Multiplikation mit $x=0$ mal wieder keine gute Idee ist, sieht man daran, dass damit aus der richtigen Aussage $4>2$ die falsche Aussage $0>0$ werden würde.

Durch die Fallunterscheidung müssen wir zwar statt einer Ungleichung mehrere lösen (abhängig von der Anzahl der zu unterscheidenden Fälle), allerdings sind diese Ungleichungen meist einfacher als die ursprüngliche Ungleichung. Da wir eine bestimmte Bedingung als gegeben annehmen, müssen wir uns um diese ja nicht mehr kümmern.
Am Ende der Rechnung ist dann wichtig, die berechneten Werte oder Intervalle mit dieser Bedingung abzugleichen. Falls sie sich widersprechen, sind die berechneten Werte oder Intervalle nämlich keine Lösungen. Alles, was wir berechnen, steht ja unter der Annahme, dass die Bedingung gilt. 
Beispiel: Rechnen wir in einem Fall unter der Bedingung, dass $x>0$ ist, kann $x=-5$ keine Lösung sein. Auch wenn unsere Rechnung, die zu $x=-5$ geführt hat, komplett korrekt ist, dürfen wir diesen Wert nicht in die Lösungsmenge aufnehmen.

Zusammengefasst kann man sagen: Ohne eine saubere Fallunterscheidung "verliert" man entweder Lösungen oder man hat am Ende zu viele - beides nicht gut ... 


Zwei Dinge müssen bei allen Fallunterscheidungen beachtet werden:

1. Es muss jeder Wert aus dem Definitionsbereich in der Fallunterscheidung beachtet werden.
   Beispiel: $x\geq\frac{1}{2}$ und $x < \frac{1}{2}$ ist eine gute Fallunterscheidung, weil jede reelle Zahl entweder größer bzw. gleich $\frac{1} {2}$ oder kleiner als $\frac{1} {2}$ ist. Hätten wir stattdessen $x>\frac{1}{2}$ und $x < \frac{1}{2}$ gewählt, wäre keine Aussage über $x=\frac{1}{2}$ möglich gewesen. Umgekehrt wäre die Zahl $\frac{1} {2}$ bei $x\geq\frac{1}{2}$ und $x\leq\frac{1}{2}$ doppelt berücksichtigt gewesen, was zu Widersprüchen führen kann.
   
   
2. Nach der Fallunterscheidung sind jeweils alle Rechenoperationen und Argumentationen, die mit dieser Voraussetzung arbeiten, erlaubt. Beispiel: Wird bei einer Fallunterscheidung angenommen, dass $x\neq 0$ ist, darf anschließend bedenkenlos durch $x$ geteilt werden, weil eine Division durch $0$ ja gar nicht vorkommen kann.

Ein paar Worte zur Lösungsmenge einer Ungleichung: Auch hier zeigt sich ein Unterschied zu Gleichungen. Während "normal lösbare" Gleichungen, wie sie in diesem Lernmodul betrachtet wurden, im Normalfall eine endliche Anzahl von Lösungen haben (z. B. quadratische Gleichungen mit einer oder zwei Lösungen), umfasst die typische Lösungsmenge bei Ungleichungen unendlich viele Zahlen. Das liegt daran, dass in Ungleichungen Größenvergleiche formuliert werden, also alle Zahlen gesucht werden, die kleiner (oder größer) als etwas Anderes sind und davon gibt es meistens eine ganze Menge ... Betrachtet man Ungleichungen im Bereich der reellen Zahlen ist die Lösungsmenge meist ein Intervall. In vielen Fällen ist es eine sehr sinnvolle Idee, die Lösungsmenge auf dem Zahlenstrahl zu veranschaulichen.

Lösungsstrategien für verschiedene Arten von Ungleichungen

Im Folgenden werden anhand von Beispielen Lösungsstrategien für verschiedene Arten von Ungleichungen eingeführt. Wenn Sie Schwierigkeiten haben, die Ungleichungsarten zu erkennen und auseinanderzuhalten, schauen Sie bitte in den entsprechenden Gleichungskapiteln nach. Quadratische Ungleichungen sind aus den gleichen Gründen "quadratisch" wie quadratische Gleichungen ...

Lineare Ungleichungen

Zunächst also lineare Ungleichungen:

Beispiel 1:
Bei einer Matheklausur gibt es pro richtige Aufgabe $5$ Punkte. Vorab konnten $8$ Bonuspunkte erarbeitet werden. Wie viele Aufgaben müssen mindestens richtig gelöst werden, wenn zum Bestehen $50$ Punkte nötig sind?
Anmerkung: Wir gehen der Einfachheit halber davon aus, dass es keine Teilpunkte für halbrichtig gelöste Aufgaben gibt.

Lösung:
Sei $x$ die Anzahl der Aufgaben in der Klausur.
Zu lösen ist die Ungleichung $8+5x \geq 50$ , wobei für $x$ nur natürliche Zahlen größer $0$ eingesetzt werden dürfen, weil ja keine Teilpunkte vergeben werden und wir davon ausgehen können, dass die Klausur aus mindestens einer Aufgabe besteht.

$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{N^+} \cr \cr 8+5x & \geq & 50 & \vert & -8 \cr\cr 5x & \geq & 42 & \vert & :5 \cr\cr x & \geq & \dfrac{42}{5} = 8{,}4 \cr \cr \mathbb{L} &=& \{9; 10; 11; \dots\} \end{array}$

Bemerkung: Sie sehen, dass der Lösungsweg quasi identisch zum Lösungsweg der entsprechenden linearen Gleichung ist. Wichtig ist noch, die $8{,}4$ auf $9$ aufzurunden, weil ja nur natürliche Zahlen als Lösungen zugelassen waren. Es muss trotz der $4$ in der Nachkommastelle aufgerundet werden, weil ja nach "mindestens" gefragt war.


Abwandlung von Beispiel 1:
Wie ändert sich die Lösung, wenn Sie erfahren, dass die Klausur $12$ Aufgaben umfasst?

Lösung:
Die zu lösende Gleichung inklusive Lösungsweg bleibt gleich, weil sich an der Punkteverteilung ja nichts geändert hat. Was sich ändert, ist der Definitionsbereich: Es kommen nun nicht mehr alle natürlichen Zahlen größer $0$ als Lösungen infrage, sondern nur noch die natürlichen Zahlen zwischen $1$ und $12$ (jeweils eingeschlossen). Formal geschrieben lautet der Definitionsbereich also: $\mathbb{D}=\{1; 2; 3; \dots; 10; 11; 12\}$
Das hat (natürlich) Auswirkungen auf die Lösungsmenge: Berechnet haben wir, dass Zahlen größer oder gleich $9$ die Ungleichung erfüllen. Davon gibt es im Definitionsbereich aber gar nicht so viele, nämlich nur $9$, $10$, $11$ und $12$. Da nur Zahlen, die im Definitionsbereich liegen, überhaupt als Lösungen infrage kommen, lautet die Lösungsmenge also: $\mathbb{L} = \{9; 10; 11; 12\}$


Beispiel 2:
Zu lösen ist $-5y+27>-3\left(\dfrac{2y}{3}-7\right)$ mit $\mathbb{D}=\mathbb{R}$

Lösung:
$\begin{array}{rclcl} -5y+27 &>& -3\left(\dfrac{2y}{3}-7\right) \cr\cr -5y+27 &>& -2y+21 & \vert & -27+2y \cr\cr -3y &>& -6 & \vert & :\left(-3\right) \cr\cr y & < & 2 \cr \cr \mathbb{L} &=& \rbrack-\infty;2\lbrack \end{array}$

Bemerkung 1: Ganz wichtig: Bei der Umformung zur letzten Zeile muss das Vergleichszeichen "umgedreht" werden, weil mit einer negativen Zahl multipliziert wurde!
Bemerkung 2: Wir haben berechnet, dass alle Zahlen aus dem Definitionsbereich, die kleiner sind als $2$, die Ungleichung lösen. Die Lösung ist also ein Teilbereich der reellen Zahlen, was man am besten als Intervall aufschreibt. Nach unten gibt es dabei keine Grenze. Mathematisch schreibt man dafür $-\infty$. Die $2$ ist nicht Teil der Lösungsmenge, weil in der letzten Zeile der Rechnung ein Kleiner- und kein Kleinergleichzeichen steht. Die Lösungsmenge ist also das offene Intervall $\rbrack-\infty;2\lbrack$. Wichtig: Das bedeutet nicht, dass das Lösungsintervall nur aus ganzen Zahlen besteht und der größte Wert im Lösungsintervall die $1$ ist. Ganz im Gegenteil: Zwischen $1$ und $2$ liegen noch etliche - um genau zu sein, unendlich viele - reelle Zahlen, die selbstverständlich ebenfalls Teil der Lösungsmenge sind, z. B. $1{,}5$.

Quadratische Ungleichungen

Es gibt verschiedene Wege, quadratische Ungleichungen zu lösen. Wir beschränken uns hier auf einen, der relativ anschaulich ist und sich leicht auf weitere Arten von Ungleichungen übertragen lässt.

Beispiel 1:
Zu lösen ist $\dfrac{1}{8}\left(2x^2-8\right) < x+2$ mit $\mathbb{D}=\mathbb{R}$

Lösung:
Wir betrachten die linke und die rechte Seite der Ungleichung jeweils als Funktion, also $f_L(x)=\dfrac{1}{8}\left(2x^2-8\right)$ und $f_R(x)=x+2$ und zeichnen die zugehörigen Graphen in ein Koordinatensystem (links). Gleichzeitig kann man die Ungleichung so umformen, dass auf der rechten Seite nur noch $0$ steht: $\dfrac{1}{4}x^2-x-3 < 0$ und ebenfalls den Graphen zur dazu passenden Funktion $f(x)= \dfrac{1}{4}x^2-x-3$ zeichnen (Koordinatensystem rechts). Das sieht dann so aus:

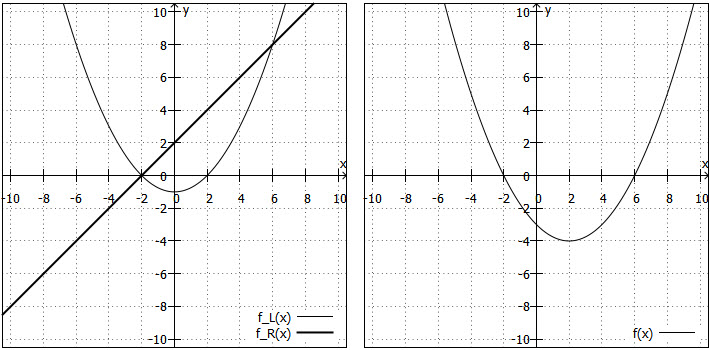
Man sieht in der linken Grafik, dass $f_L(x)$ zwischen $-2$ und $6$ kleiner als $f_R(x)$ ist. Die Lösungsmenge lautet daher $\mathbb{L}=\;\rbrack-2;6\lbrack$. Alternativ suchen wir in der rechten Grafik den Bereich, in dem $f(x)$ kleiner als $0$ ist.
Die Lösung der Ungleichung lässt sich also direkt aus der Grafik ablesen - mit der Einschränkung, dass das natürlich nur funktioniert, wenn die Schnittpunkte bei "glatten" Zahlenwerten liegen (werden wir gleich bestätigen). Lägen die Schnittpunkte z. B. bei $-1{,}9897$ und $6{,}001203$, hätten wir mit dieser Methode keine Chance ... Trotzdem lohnen sich Zeichnungen in vielen Fällen, vor allem auch bei komplizierteren Ungleichungen, weil man dadurch zumindest eine Idee bekommt, wie die Lösung aussehen muss.


Rechnerisch nähern wir uns der Lösung, indem wir die zugehörige quadratische Gleichung betrachten, am geschicktesten direkt von der bereits umgeformten Ungleichung: $\frac{1}{4}x^2-x-3=0$ . Darüber lassen sich nämlich die Stellen, an denen $f(x)$ Nullstellen hat, was ja den Rändern des Lösungsintervalls entspricht, exakt ermitteln. Wie man oben in der rechten Grafik sieht, ist die Funktion zwischen zwei Nullstellen entweder immer positiv oder immer negativ. D. h., wir müssen dann nur noch untersuchen, welcher Fall in welchem Teilintervall eintritt (Kleine Einschränkung: Das funktioniert nicht, wenn die Funktion Sprünge, Löcher etc. haben sollte, aber solche Funktionen betrachten wir hier nicht.). Also:

$\begin{array}{rclcl} \dfrac{1}{4}x^2-x-3 &=& 0 & \vert & \cdot 4 \cr\cr x^2-4x-12 &=& 0 \cr x_{1,2} &=& 2\pm\sqrt{4+12} \cr x_{1,2} &=& 2\pm\sqrt{16} \cr \cr x_1 &=& 2+4 \; = \; 6 \cr x_2 &=& 2-4 \; = \; -2 \end{array}$

Diese Werte liefern uns drei Intervalle:
Von $-\infty$ bis zur kleineren Nullstelle, hier $x_2$: $I_1=\;\rbrack-\infty;-2\lbrack$
Zwischen den Nullstellen: $I_2=\;\rbrack-2;6\lbrack$
Von der größeren Nullstelle, hier $x_1$, bis $+\infty$ : $I_3=\;\rbrack6;\infty\lbrack$

Wichtig: Die ermittelten Nullstellen, im vorliegenden Fall $-2$ und $6$, werden nicht in die offenen Intervalle eingeschlossen. Bei Ungleichungen, die ein Kleiner- oder Größerzeichen enthalten, können die Nullstellen niemals eine Lösung der Ungleichung sein. Handelt es sich um Ungleichungen, die ein Kleinergleich- oder Größergleichzeichen enthalten, stellen die Nullstellen immer eine Lösung der Ungleichung dar. Bei den Nullstellen sollte man also genau hinschauen.

Nun müssen wir noch überprüfen, wo $f(x)$ größer als $0$ und wo $f(x)$ kleiner als $0$ ist, denn das war ja die eigentliche Frage. (Letztendlich kann man das natürlich auch aus den Grafiken oben ablesen, aber hier soll ein vollständiger Rechenweg gezeigt werden.) Das machen wir, indem wir einzelne Werte aus den drei Intervallen in den ursprünglichen Term einsetzen. Welche Zahlen wir dabei nehmen, ist egal, denn innerhalb der Intervalle gibt es ja entweder nur positive oder nur negative Funktionswerte. Wir dürfen uns also jeweils eine Zahl aussuchen, mit der es sich besonders schön weiterrechnet:
Für $I_1$ nehmen wir $-4$: $f(-4)=\frac{1}{4}\cdot 16+4-3=5>0$ Also kommt $I_1$ nicht als Lösung infrage.
Für $I_2$ nehmen wir $0$: $f(0)=\frac{1}{4}\cdot 0-0-3=-3 < 0$ Hier passt es: $I_2$ kommt als Lösung infrage.
Für $I_3$ nehmen wir $8$: $f(8)=\frac{1}{4}\cdot 64-8-3=5>0$ Also kommt $I_3$ auch nicht als Lösung infrage.

Bemerkung: Warum wurden gerade diese Zahlen für die Überprüfung der Intervalle gewählt?
$0$ ist eigentlich immer eine gute Option, weil damit alle Produkte wegfallen. $-4$ und $8$ haben den Vorteil, dass sie die betragsmäßig kleinsten Zahlen aus den beiden Intervallen sind, die quadriert durch $4$ teilbar sind. Anders gesagt: Für diese Zahlen liefert $\frac{1}{4}x^2$ eine ganze Zahl und keinen Bruch. Man könnte für $I_3$ natürlich auch mit $\frac{6{,}12^2}{4}=\frac{37{,}4544}{4}$ oder mit $\frac{7^2}{4}=\frac{49}{4}$ weiter rechnen, wäre vollkommen korrekt - aber wenn die Alternative $\frac{8^2}{4}=16$ ist ...

In die Lösungsmenge einer Ungleichung gehen grundsätzlich alle Intervalle ein, in denen die Überprüfung eine wahre Aussage ergibt. Da unsere Beispielungleichung ein Kleinerzeichen enthält, sind die Nullstellen nicht Teil der Lösung. Wir erhalten also als Lösungsmenge $\mathbb{L}=\;\rbrack-2;6\lbrack$.

Bemerkung: Die Dreiteilung des möglichen Lösungsbereiches ist recht typisch für quadratische Ungleichungen. Wenn Sie sich an den klassischen Verlauf von Parabeln mit zwei Nullstellen erinnern, wissen Sie auch warum. Die Lösung besteht dann entweder aus dem mittleren Intervall oder den beiden äußeren.
Allerdings ist es auch möglich, dass die Parabel die x-Achse gar nicht schneidet oder lediglich in einem Punkt berührt. Dann sieht der Lösungsbereich entsprechend anders aus. Ein Beispiel dafür folgt nun:


Beispiel 2:
Schauen wir uns die Ungleichung $-25x^2+130x\geq 169$ mit $\mathbb{D}=\mathbb{R}$ an:
$\begin{array}{rclcll}-25x^2+130x-169 &\geq & 0 &\vert & :\left(-25\right)\\x^2-\dfrac{26}{5}x+\dfrac{169}{25} &\leq & 0 \end{array}$

Wir betrachten nun die zugehörige quadratische Gleichung:
$\begin{array}{rclcl}x^2-\dfrac{26}{5}x+\dfrac{169}{25} &=& 0 &\vert& \text{p-q-Formel} \\ x_{1,2} &=& \dfrac{13}{5}\pm\sqrt{\left(-\dfrac{13}{5}\right)^2-\dfrac{169}{25}} \\\\x_{1,2} &=& \dfrac{13}{5}\pm\sqrt{0} \\\\x_{1,2} &=& \dfrac{13}{5}\end{array}$

In diesem Fall bekommen wir nur zwei Intervalle:
Von $-\infty$ bis zur Nullstelle: $I_1=\;\left\rbrack-\infty;\dfrac{13}{5}\right\lbrack$
Von der Nullstelle bis $+\infty$ : $I_2=\;\left\rbrack \dfrac{13}{5};\infty\right\lbrack$

Nun müssen wir überprüfen, wo die linke Seite der Ungleichung kleiner oder gleich $0$ ist; denn das war ja die eigentliche Frage:
Für $I_1$ nehmen wir $0$: $0^2-\dfrac{26}{5} \cdot 0+\dfrac{169}{25} = \dfrac{169}{25} > 0$ Also kommt $I_1$ nicht als Lösung infrage.
Für $I_2$ nehmen wir $5$: $5^2-\dfrac{26}{5} \cdot 5+\dfrac{169}{25} = \dfrac{144}{25} > 0$ Auch $I_2$ kommt als Lösung nicht infrage.

Die Intervallbetrachtung liefert uns also keine Lösungen der Ungleichung. Aber: Da die ursprüngliche Ungleichung ein Größergleichzeichen enthält, ist die oben berechnete Lösung der quadratischen Gleichung Teil der Lösungsmenge. Diese Ungleichung wird also von einem einzigen Wert erfüllt: $\mathbb{L} = \left\{\dfrac{13}{5}\right\}$

Grafische Interpretation: Betrachtet man die zugehörige quadratische Funktion $f(x) = x^2-\dfrac{26}{5}x+\dfrac{169}{25}$, hat die Parabel nur eine Nullstelle, nämlich bei $x_N = \dfrac{13}{5}$. Sie berührt die x-Achse also nur. Da der Koeffizient von $x^2$ positiv ist, ist die Parabel nach oben geöffnet. Deshalb verläuft sie links und rechts vom Berührpunkt oberhalb der Achse. Für die Lösung der Ungleichung $x^2-\dfrac{26}{5}x+\dfrac{169}{25} \leq 0$, also als Antwort auf die Frage, wo die Werte der Parabel auf oder unterhalb der x-Achse liegen, kommt also nur die Nullstelle infrage.

Beispiel 3:
Abschließend wollen wir das Beispiel $8y^2-32 \leq 0$ mit $\mathbb{D} = \mathbb{R}$ betrachten:
$\begin{array}{rclcl} 8y^2-32 &\leq& 0 &\vert& +32 \\ 8y^2 &\leq& 32 &\vert& :8 \\ y^2 &\leq& 4 \end{array}$
Jetzt könnte man auf die Idee kommen, auf beiden Seiten die Wurzel zu ziehen mit dem Ergebnis $y \leq 2$. Das ist nicht ganz verkehrt, aber leider auch nicht ganz richtig ... $y \leq 2$ entspricht ja dem Intervall $]-\infty; 2]$ und in diesem Intervall sind viele Zahlen enthalten, die unsere Ungleichung $y^2 \leq 4$ nicht erfüllen, z. B. $y_1=-5$ mit $y_1^2 = 25$. Wir müssen das Intervall also auch nach unten beschränken. Die kleinste Zahl, die die Ungleichung erfüllt, ist $-2$, also die Gegenzahl zu dem schon gefundenen Wert $2$. Das führt uns zu dem Lösungsintervall $[-2;2]$. Die Lösung ist also nicht $y \leq 2$, sondern $-2 \leq y \leq 2$, was das gleiche ist wie $\vert y\vert \leq 2$. In Worten: Der Betrag von $y$ muss kleiner oder gleich $2$ sein.

Die vollständige Lösung der Beispielungleichung lautet also
$\begin{array}{rclcl} 8y^2-32 &\leq& 0 &\vert& +32 \\ 8y^2 &\leq& 32 &\vert& :8 \\ y^2 &\leq& 4 &\vert& \sqrt{} \\ \vert y \vert &\leq& 2 \\\\\mathbb{L} &=& [-2;2]\end{array}$

Bemerkung 1: Die Argumentation funktioniert genauso, wenn in der Ungleichung $<$ statt $\leq$ steht, nur dass wir dann statt des abgeschlossenen Intervalls $[-2;2]$ das offene Intervall $]-2;2[$ erhalten, welches $-2 < y < 2$ entspricht.
Bemerkung 2: Bei Ungleichungen mit $\geq$ oder $>$ muss ebenfalls beim Wurzelziehen der Betrag gesetzt werden. Ohne den Betrag würden wir in diesem Fall nämlich viele Lösungen verlieren. Beispiel: Würde man aus $y^2 \geq 4$ folgern, dass $y \geq 2$ ist, dann fehlten alle negativen Lösungen der Ungleichungen, wie $y_2=-10$ mit $y_2^2=100$, was ja offensichtlich größer gleich $4$ ist. Also ist hier die richtige Lösung $\vert y\vert \geq 2$.
Bemerkung 3: Vielleicht haben Sie bei dieser Aufgabe an quadratische Gleichungen, wie $y^2 = 4$, gedacht und daran, dass hier die Lösung $y=\pm 2$ ist ... Da man diese Lösung auch mit einem Betrag schreiben kann, nämlich als $\vert y\vert =2$, sind sich Gleichungen und Ungleichungen auch hier wieder sehr ähnlich.

Bruchungleichungen

Schauen wir uns zum Abschluss noch eine Ungleichung an, bei der eine Fallunterscheidung vorgenommen werden muss. Leider müssen wir hierfür ein bisschen vorgreifen, da der grundsätzliche Lösungsweg für Bruch(un)gleichungen erst im Kapitel 14 erläutert wird ... Wir beschränken uns daher hier auf einen einfachen Fall.

Beispiel:
Zu lösen ist $\dfrac{12-x}{4x-8} \leq 1$

Bestimmung des Definitionsbereichs:
Da nicht durch $0$ geteilt werden darf, muss der Nenner $4x-8$ ungleich $0$ sein. Daher müssen wir zunächst mithilfe einer Ungleichung ausrechnen, für welche Variablenwerte diese Bedingung erfüllt wird, und den Definitionsbereich entsprechend "zuschneiden".
$\begin{array}{rclcll}4x-8 &\neq & 0 &\vert & +8 \\4x &\neq & 8 &\vert & :4\\x &\neq & 2\end{array}$

Aus der Betrachtung der Lösung können wir ableiten, dass wir alle Werte aus $\mathbb{R}$ mit Ausnahme der $2$ verwenden dürfen. Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\left\{2\right\}}$.

Lösung der Ungleichung:
$\begin{array}{rclcll}\dfrac{12-x}{4x-8} &\leq & 1 &\vert & \cdot\left(4x-8\right)\end{array}$
Wir multiplizieren die Ungleichung mit dem Nenner $(4x-8)$, um den Bruch auflösen. Da wir dabei mit der Variablen multiplizieren, ist eine Fallunterscheidung nötig. Wir wissen ja nicht, ob der Term, mit dem wir die Ungleichung multiplizieren, positiv oder negativ ist.

Fall 1: Wir nehmen an, dass $4x-8>0$ ist, also $x>2$. Dann bleibt das Vergleichszeichen, wie es ist:
$\begin{array}{rclcll}\dfrac{12-x}{4x-8} &\leq & 1 &\vert & \cdot\left(4x-8\right) \\12-x &\leq & 4x-8 &\vert & +8+x \\20 &\leq & 5x &\vert & :5 \\4 &\leq & x \\x &\geq& 4\end{array}$

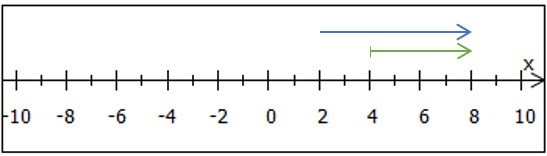
Als Ergebnis unserer Rechnung erhalten wir die Bedingung $x \geq 4$ (grüner Pfeil in der Grafik unten), die wir mit der Eintrittsbedingung unserer Fallunterscheidung $x>2$ (blauer Pfeil) abgleichen müssen. Beiden Bedingungen gemeinsam ist nur der Zahlenbereich $x\geq 4$, auch wenn $x>2$ noch weitere Bereiche umfasst, z. B. die Zahl $3$, die zwar größer als $2$, aber nicht größer gleich $4$ ist. Die Teillösungsmenge für diesen Fall der Fallunterscheidung ist also $\mathbb{L}_1 = \left[4;\infty\right[$.


Fall 2: Wir nehmen an, dass $4x-8 < 0$ ist, also $x < 2$. Nun muss das Vergleichszeichen "umgedreht" werden, weil wir mit einem negativen Faktor multiplizieren:
$\begin{array}{rclcll}\dfrac{12-x}{4x-8} &\leq & 1 &\vert & \cdot\left(4x-8\right)\\12-x &\geq & 4x-8 &\vert & +8+x\\20 &\geq & 5x &\vert & :5\\4 &\geq & x \\x &\leq& 4\end{array}$

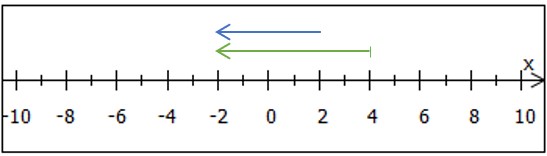
In diesem Fall bekommen wir als Ergebnis die Bedingung $x \leq 4$ (grüner Pfeil), die wir wieder mit der Eintrittsbedingung $x < 2$ (blauer Pfeil) abgleichen. Beide Bedingungen sind im Zahlenbereich $x < 2$ erfüllt. Daraus ergibt sich die Teillösungsmenge $\mathbb{L}_2 = \left]-\infty ; 2\right[$.


Ergebnis: Für die Gesamtlösungsmenge müssen wir noch die Teillösungsmengen vereinigen: 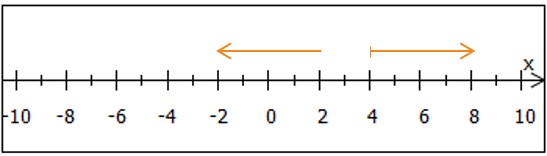$\mathbb{L} = \mathbb{L}_1 \cup \mathbb{L}_2 = \left]-\infty ; 2\right[ \cup \left[4;\infty\right[$


Bemerkung 1: Die Gesamtlösungsmenge lässt sich leider nicht einfacher aufschreiben ...

Bemerkung 2: Oben wurde erläutert, dass bei einer Fallunterscheidung immer alle Werte des Definitionsbereichs berücksichtigt werden müssen. In diesem Beispiel sieht es vielleicht auf den ersten Blick so aus, als hätten wir $4x-8=0$ bei der Fallunterscheidung "vergessen". Allerdings steht $4x-8$ in dieser Ungleichung im Nenner und dieser darf ja von vorneherein nicht $0$ sein. Daher hatten wir den Fall $4x-8=0$ über die Bestimmung des Definitionsbereichs schon ausgeschlossen.