Übersicht:

• Lösung zur 1. Aufgabe
• Lösung zur 2. Aufgabe
• Lösung zur 3. Aufgabe
• Lösung zur 4. Aufgabe
• Lösung zur 5. Aufgabe
• Lösung zur 6. Aufgabe
• Lösung zur 7. Aufgabe
• Lösung zur 8. Aufgabe
• Lösung zur 9. Aufgabe
• Lösung zur 10. Aufgabe
• Lösung zur 11. Aufgabe
• Lösung zur 12. Aufgabe
• Lösung zur 13. Aufgabe
• Lösung zur 14. Aufgabe

20.3 Geometrie - Lösungen

Erste Bemerkung vorab: Für die folgenden Aufgaben ist eine Skizze der jeweiligen Figur, aus der ersichtlich wird, welche Größe wie benannt ist, notwendig für eine vollständige Lösung (und für den Überblick auch ...). Um die Lösungen hier nicht zu lang werden zu lassen, beziehen sich die Lösungen der Aufgabe 1. bis 4. auf die Skizzen auf der vorherigen Seite.
Zweite Bemerkung vorab: Da die Variablen bei diesen Aufgaben alle für geometrische Objekte (meistens Strecken) stehen, dürfen wir davon ausgehen, dass sie eine messbare Länge haben. Beim Umformen der Formeln (z. B. bei Aufgabe 5.1) können eine Division durch oder eine Multiplikation mit $0$ also nicht auftreten.

1. Aufgabe

1)

2)

Bemerkung: $1 \,m$ sind $100 \,cm$ und $1 \,m^2$ sind $10.000 \,cm^2$.

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

2. Aufgabe

1)

2)

3)

3. Aufgabe

1)

2)

3)

4. Aufgabe

Bemerkung: In der Mathematik ist es - anders als in der Physik - üblich, die Einheiten während der Rechnung nicht hinzuschreiben. Erst im Antwortsatz, der bei Textaufgaben dazugehört, muss die Einheit notiert werden.

1)
Seien $r_1$ der Radius und $A_1$ der Flächeninhalt des Kreises $K_1$.
Dann gilt:
$\begin{array}{rcl} A_1 &=& \pi \cdot r_1^2 \cr &=& \pi \cdot 10^2 \cr &=& 100\pi \end{array}$

Seien $r_2$ der Radius und $A_2$ der Flächeninhalt des Kreises $K_2$ mit dem doppelten Flächeninhalt von $K_1$.
Dann gilt:
$\begin{array}{rcl} A_2 &=& 2A_1 \cr &=& 200\pi \end{array}$

Nun ist ja aber auch $A_2=\pi \cdot r_2^2$ und damit also
$\begin{array}{rclcl} 200 \pi &=& \pi r_2^2 &\vert& : \pi \cr 200 &=& r_2^2 &\vert& \sqrt{} \cr r_2 &=& \sqrt{200} \cr &\approx& 14{,}14 \end{array}$

Der Radius $r_2$ des Kreises mit doppeltem Flächeninhalt ist ungefähr $14{,}14 \, m$ lang.

2)
Sei $A_1$ der Flächeninhalt des Quadrates $Q_1$.
Seien $a_2$ die Seite und $A_2$ der Flächeninhalt des Quadrates $Q_2$, das den halben Flächeninhalt von $Q_1$ hat.
Dann gilt:
$\begin{array}{rclcl} A_2 &=& 0{,}5 \cdot A_1 \cr &=& 0{,}5 \cdot 16 \cr &=& 8 \cr \cr\cr A_2 &=& a_2^2 \cr\cr 8 &=& a_2^2 &\vert& \sqrt{} \cr\cr a_2 &=& \sqrt{8} \cr\cr &\approx& 2{,}83 \end{array}$

Die Seite $a_2$ des Quadrats mit halbem Flächeninhalt ist ungefähr $2{,}83 \, cm$ lang.

5. Aufgabe

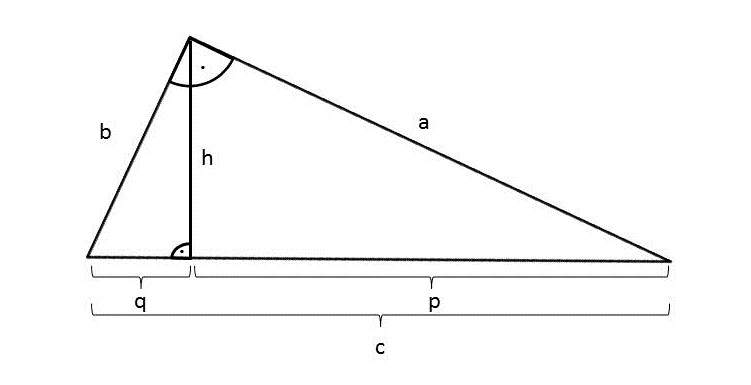1)
Berechne $c$ mit dem Satz des Pythagoras im großen Dreieck:
$\begin{array}{rclcc} a^2+b^2 &=& c^2 & \vert & \sqrt{} \cr c &=& \sqrt{a^2+b^2} \cr &=& \sqrt{3^2+4^2} \cr &=& \sqrt{25} \cr &=& 5 \, cm \end{array}$

Berechne $p$ mit einem der Kathetensätze:
$\begin{array}{rclcc} a^2 &=& c \cdot p & \vert & :c \cr p &=& \dfrac{a^2}{c} \cr \cr &=& \dfrac{3^2}{5} \cr \cr &=& \dfrac{9}{5} \, cm \end{array}$

Berechne $q$:
$\begin{array}{rclcc} p+q &=& c & \vert & -p \cr q &=& c-p \cr &=& 5- \dfrac{9}{5} \cr &=& \dfrac{16}{5} \, cm \end{array}$

Berechne $h$ mit dem Höhensatz:
$\begin{array}{rclcc} h^2 &=& p \cdot q & \vert & \sqrt{} \cr h &=& \sqrt{p \cdot q} \cr &=& \sqrt{\dfrac{9}{5} \cdot \dfrac{16}{5}} \cr \cr &=& \sqrt{ \dfrac{144}{25}} \cr \cr &=& \dfrac{12}{5} \, cm \end{array}$

 
2)
Berechne $q$ mit dem Höhensatz:
$\begin{array}{rclcc} h^2 &=& p \cdot q & \vert & :p \cr q &=& \dfrac{h^2}{p} \cr \cr &=& \dfrac{5^2}{5} \cr &=& 5 \, cm \end{array}$

Berechne $c$:
$\begin{array}{rclcc} c &=& p+q \cr &=& 5+5 \cr &=& 10 \, cm \end{array}$

Berechne $b$ mit dem Satz des Pythagoras im linken Teildreieck:
$\begin{array}{rclcc} h^2+q^2 &=& b^2 & \vert & \sqrt{} \cr b &=& \sqrt{h^2+q^2} \cr &=& \sqrt{5^2+5^2} \cr &=& \sqrt{50} \cr & \approx & 7{,}07 \, cm \end{array}$

Berechne $a$ mit dem Satz des Pythagoras im rechten Teildreieck:
$\begin{array}{rclcc} h^2+p^2 &=& a^2 & \vert & \sqrt{} \cr a &=& \sqrt{h^2+p^2} \cr &=& \sqrt{5^2+5^2} \cr &=& \sqrt{50} \cr & \approx & 7{,}07 \, cm \end{array}$

Bemerkung: Die Gleichheit der Katheten $a$ und $b$ hätte man auch schon zu Beginn der Rechnung erkennen können. In solch einem Fall muss die Rechnung natürlich nicht in aller Ausführlichkeit noch einmal aufgeschrieben werden.

 
3)
Berechne $b$ mit dem Satz des Pythagoras im großen Dreieck:
$\begin{array}{rclcc} a^2+b^2 &=& c^2 & \vert & -a^2 \cr b^2 &=& c^2-a^2 & \vert & \sqrt{} \cr b &=& \sqrt{c^2-a^2} \cr &=& \sqrt{6{,}1^2-3{,}4^2} \cr & \approx & 5{,}06 \, cm \end{array}$

Berechne $p$ mit einem der Kathetensätze:
$\begin{array}{rclcc} a^2 &=& c \cdot p & \vert & :c \cr p &=& \dfrac{a^2}{c} \cr \cr &=& \dfrac{3{,}4^2}{6{,}1} \cr & \approx & 1{,}90 \, cm \end{array}$

Berechne $q$:
$\begin{array}{rclcc} p+q &=& c & \vert & -p \cr q &=& c-p \cr &\approx& 6{,}1-1{,}90 \cr &\approx& 4{,}20 \, cm \end{array}$

Berechne $h$ mit dem Höhensatz:
$\begin{array}{rclcc} h^2 &=& p \cdot q & \vert & \sqrt{} \cr h &=& \sqrt{p \cdot q} \cr &\approx& \sqrt{1{,}90 \cdot 4{,}20} \cr &\approx& \sqrt{7{,}98} \cr & \approx & 2{,}82 \, cm \end{array}$

 
4)
Berechne $c$ mit einem der Kathetensätze:
$\begin{array}{rclcc} b^2 &=& q \cdot c & \vert & :q \cr c &=& \dfrac{b^2}{q} \cr \cr &=& \dfrac{5{,}2^2}{1{,}2} \cr & \approx & 22 {,}53 \, cm \end{array}$

Berechne $a$ mit dem Satz des Pythagoras im großen Dreieck:
$\begin{array}{rclcc} a^2+b^2 &=& c^2 & \vert & -b^2 \cr a^2 &=& c^2-b^2 & \vert & \sqrt{} \cr a &=& \sqrt{c^2-b^2} \cr &\approx& \sqrt{22{,}53^2-5{,}2^2} \cr &\approx& \sqrt{480{,}71} \cr & \approx & 21{,}93 \, cm \end{array}$

Berechne $p$:
$\begin{array}{rclcc} p+q &=& c & \vert & -q \cr p &=& c-q \cr &\approx& 22{,}53-1{,}2 \cr &\approx& 21{,}33 \, cm \end{array}$

Berechne $h$ mit dem Höhensatz:
$\begin{array}{rclcc} h^2 &=& p \cdot q & \vert & \sqrt{} \cr h &=& \sqrt{p \cdot q} \cr &\approx& \sqrt{21{,}33 \cdot 1{,}2} \cr &\approx& \sqrt{25{,}60} \cr & \approx & 5{,}06 \, cm \end{array}$

 
5)
Berechne $q$:
$\begin{array}{rclcc} p+q &=& c & \vert & -p \cr q &=& c-p \cr &=& 7-3{,}9 \cr &=& 3{,}1 \, cm \end{array}$

Berechne $h$ mit dem Höhensatz:
$\begin{array}{rclcc} h^2 &=& p \cdot q & \vert & \sqrt{} \cr h &=& \sqrt{p \cdot q} \cr &=& \sqrt{3{,}1 \cdot 3{,}9} \cr &=& \sqrt{12{,}09} \cr & \approx & 3{,}48 \, cm \end{array}$

Berechne $a$ mit dem Satz des Pythagoras im rechten Teildreieck:
$\begin{array}{rclcc} h^2+p^2 &=& a^2 & \vert & \sqrt{} \cr a &=& \sqrt{h^2+p^2} \cr &\approx& \sqrt{3{,}48^2+3{,}9^2} \cr &\approx& \sqrt{27{,}3} \cr & \approx & 5{,}22 \, cm \end{array}$

Berechne $b$ mit dem Satz des Pythagoras im großen Dreieck:
$\begin{array}{rclcc} a^2+b^2 &=& c^2 & \vert & -a^2 \cr b^2 &=& c^2-a^2 & \vert & \sqrt{} \cr b &=& \sqrt{c^2-a^2} \cr &\approx& \sqrt{7^2-5{,}22^2} \cr &\approx& \sqrt{21{,}7} \cr & \approx & 4{,}66 \, cm \end{array}$

6)
Berechne $h$ mit dem Satz des Pythagoras im rechten Teildreieck
$\begin{array}{rclcc}a^2 &=& h^2+p^2 &\vert & -p^2\\h^2 &=& a^2-p^2 &\vert & \sqrt{}\\h &=& \sqrt{a^2-p^2} \\&=& \sqrt{2{,}8^2-1^2} \\&\approx & 2{,}62\, mm\end{array}$

Berechne $q$ mit dem Höhensatz
$\begin{array}{rclcc}h^2 &=& p\cdot q &\vert & :p\\\\q &=& \dfrac{h^2}{p} \\&\approx& \dfrac{2{,}62^2}{1} \\&\approx & 6{,}86\, mm\end{array}$

Berechne $c$
$\begin{array}{rclcc}c &=& p + q \\&\approx& 1+6{,}86 \\&\approx& 7{,}86\, mm\end{array}$

Berechne $b$ mit dem Satz des Pythagoras im großen Dreieck
$\begin{array}{rclcc}c^2 &=& a^2+b^2 &\vert &-a^2\\b^2 &=& c^2-a^2 &\vert &\sqrt{}\\b &=& \sqrt{c^2-a^2}\\&\approx& \sqrt{7{,}86^2-2{,}8^2}\\&\approx & 7{,}34\, mm\end{array}$

7)
Berechne $c$ mit dem Satz des Pythagoras im großen Dreieck
$\begin{array}{rclcc}c^2 &=& a^2+b^2 &\vert &\sqrt{}\\c &=& \sqrt{a^2+b^2}\\&=& \sqrt{16^2+9^2}\\&\approx & 18{,}36\, cm\end{array}$

Berechne $p$ mit einem der Kathetensätze
$\begin{array}{rclcc}a^2 &=& c\cdot p &\vert & :c\\\\p &=& \dfrac{a^2}{c}\\&\approx& \dfrac{16^2}{18{,}36}\\&\approx & 13{,}94\, cm\end{array}$

Berechne $q$
$\begin{array}{rclcc}c &=& p+q &\vert & -p\\q &=& c-p \\&\approx& 18{,}36-13{,}94\\&\approx& 4{,}42\, cm\end{array}$

Berechne $h$ mit dem Höhensatz
$\begin{array}{rclcc}h^2 &=& p\cdot q &\vert &\sqrt{}\\h &=& \sqrt{p\cdot q}\\&\approx& \sqrt{13{,}94\cdot 4{,}42}\\&\approx & 7{,}85\, cm\end{array}$

8)
Berechne $b$ mit dem Satz des Pythagoras im linken Teildreieck
$\begin{array}{rclcc}b^2 &=& h^2+q^2 &\vert &\sqrt{}\\b &=& \sqrt{h^2+q^2}\\&=& \sqrt{403^2+507^2} \\&\approx & 647{,}66\, cm\end{array}$

Berechne $c$ mit einem der Kathetensätze
$\begin{array}{rclcc}b^2 &=& c\cdot q &\vert & :q\\\\c &=& \dfrac{b^2}{q}\\&\approx& \dfrac{647{,}66^2}{507}\\&\approx & 827{,}34\, cm\end{array}$

Berechne $p$
$\begin{array}{rclcc}c &=& p+q &\vert &-q\\p &=& c-q \\&\approx& 827{,}34-507\\&\approx& 320{,}34\, cm\end{array}$

Berechne $a$ mit dem Satz des Pythagoras im rechten Teildreieck
$\begin{array}{rclcc}a^2 &=& h^2+p^2 &\vert &\sqrt{}\\a &=& \sqrt{h^2+p^2}\\&\approx& \sqrt{403^2+320{,}34^2}\\&\approx& 514{,}81\,cm\end{array}$

9)
Berechne $b$ mit dem Satz des Pythagoras im großen Dreieck
$\begin{array}{rclcc}c^2 &=& a^2+b^2 &\vert &-a^2\\b^2 &=& c^2-a^2 &\vert &\sqrt{}\\b &=& \sqrt{c^2-a^2}\\&=& \sqrt{3{,}1416^2-2{,}7183^2}\\&\approx & 1{,}5750\, km\end{array}$

Berechne $q$ mit einem der Kathetensätze
$\begin{array}{rclcc}b^2 &=& c\cdot q &\vert & :c\\\\q &=& \dfrac{b^2}{c}\\&\approx& \dfrac{1{,}575^2}{3{,}1416}\\&\approx & 0{,}7896\, km\end{array}$

Berechne $p$
$\begin{array}{rclcc}c &=& p+q &\vert & -q\\p &=& c-q\\&\approx& 3{,}1416-0{,}7896\\&\approx& 2{,}352\, km\end{array}$

Berechne $h$ mit dem Höhensatz
$\begin{array}{rclcc}h^2 &=& p\cdot q &\vert &\sqrt{} \\h &=&\sqrt{p\cdot q}\\&\approx& \sqrt{2{,}352\cdot 0{,}7896}\\&\approx & 1{,}3628\, km\end{array}$

10)
Berechne $p$
$\begin{array}{rclcc}c &=& p+q &\vert &-q\\p &=& c-q\\&=& 5{,}34-0{,}2\\&=& 5{,}14\, cm\end{array}$

Berechne $h$ mit dem Höhensatz
$\begin{array}{rclcc}h^2 &=& p\cdot q &\vert &\sqrt{}\\h &=& \sqrt{p\cdot q}\\&=& \sqrt{5{,}14\cdot 0{,}2}\\&\approx & 1{,}01\, cm\end{array}$

Berechne $b$ mit einem der Kathetensätze
$\begin{array}{rclcc}b^2 &=& c\cdot q &\vert &\sqrt{}\\b &=& \sqrt{c\cdot q}\\&=& \sqrt{5{,}34\cdot 0{,}2}\\&\approx & 1{,}03\, cm\end{array}$

Berechne $a$ mit einem der Kathetensätze
$\begin{array}{rclcc}a^2 &=& c\cdot p &\vert &\sqrt{}\\a &=& \sqrt{c\cdot p}\\&=& \sqrt{5{,}34\cdot 5{,}14}\\&\approx & 5{,}24\, cm\end{array}$

11)
Berechne $h$ mit dem Satz des Pythagoras im linken Teildreieck
$\begin{array}{rclcc}b^2 &=& q^2+h^2 &\vert &-q^2\\h^2 &=& b^2-q^2 &\vert &\sqrt{}\\h &=& \sqrt{b^2-q^2}\\&=& \sqrt{603^2-60{,}3^2}\\&\approx & 599{,}98\, cm\end{array}$

Berechne $c$ mit einem der Kathetensätze
$\begin{array}{rclcc}b^2 &=& c\cdot q &\vert & :q \\c &=& \dfrac{b^2}{q}\\&=& \dfrac{603^2}{60{,}3}\\&=& 6.030\, cm\end{array}$

Berechne $a$ mit dem Satz des Pythagoras
$\begin{array}{rclcc}c^2 &=& a^2+b^2 &\vert &-b^2\\a^2 &=& c^2-b^2 &\vert &\sqrt{}\\a &=& \sqrt{c^2-b^2}\\&=& \sqrt{6.030^2-603^2}\\&\approx & 5.999{,}77\, cm\end{array}$

Berechne $p$
$\begin{array}{rclcc}c &=& p+q &\vert &-q\\p &=& c-q\\&=& 6.030-60{,}3\\&=& 5.969{,}7\, cm\end{array}$

12)
Berechne $c$
$\begin{array}{rclcc}c &=& p+q\\&=& 0{,}3+0{,}5\\&=& 0{,}8\, cm\end{array}$

Berechne $h$ mit dem Höhensatz
$\begin{array}{rclcc}h^2 &=& p\cdot q &\vert &\sqrt{}\\h &=& \sqrt{p\cdot q}\\&=& \sqrt{0{,}3\cdot 0{,}5}\\&\approx & 0{,}39\, cm\end{array}$

Berechne $b$ mit dem Satz des Pythagoras im linken Teildreieck
$\begin{array}{rclcc}b^2 &=& q^2+h^2 &\vert &\sqrt{}\\b &=& \sqrt{q^2+h^2}\\&\approx& \sqrt{0{,}5^2+0{,}39^2}\\&\approx & 0{,}63\, cm\end{array}$

Berechne $a$ mit dem Satz des Pythagoras
$\begin{array}{rclcc}a^2 &=& h^2+p^2 &\vert &\sqrt{}\\a &=& \sqrt{h^2+p^2}\\&\approx& \sqrt{0{,}39^2+0{,}3^2}\\&\approx & 0{,}49\, cm\end{array}$

13)
Berechne $c$ mit dem Satz des Pythagoras im großen Dreieck
$\begin{array}{rclcc}c^2 &=& a^2+b^2 &\vert &\sqrt{} \\c &=& \sqrt{a^2+b^2} \\&=& \sqrt{50^2+50^2}\\&\approx & 70{,}71\, cm\end{array}$

Berechne $p$ mit einem der Kathetensätze
$\begin{array}{rclcc}a^2 &=& c\cdot p &\vert & :c\\\\p &=& \dfrac{a^2}{c}\\&\approx& \dfrac{50^2}{70{,}71}\\&\approx & 35{,}36\, cm\end{array}$

Berechne $q$ mit einem der Kathetensätze
$\begin{array}{rclcc}b^2 &=& c\cdot q &\vert & :c\\\\q &=& \dfrac{b^2}{c}\\&\approx& \dfrac{50^2}{70{,}71}\\&\approx & 35{,}36\, cm\end{array}$

Berechne $h$ mit dem Höhensatz
$\begin{array}{rclcc}h^2 &=& p\cdot q &\vert &\sqrt{}\\h &=& \sqrt{p\cdot q}\\&\approx& \sqrt{35{,}36\cdot 35{,}36}\\&\approx & 35{,}36\, cm\end{array}$

14)
Berechne $a$ mit dem Satz des Pythagoras im großen Dreieck
$\begin{array}{rclcc}c^2 &=& a^2+b^2 &\vert &-b^2\\a^2 &=& c^2-b^2 &\vert &\sqrt{}\\a &=& \sqrt{c^2-b^2}\\&=& \sqrt{753^2-456^2}\\&\approx & 599{,}23\, cm\end{array}$

Berechne $q$ mit einem der Kathetensätze
$\begin{array}{rclcc}b^2 &=& c\cdot q &\vert & :c\\\\q &=& \dfrac{b^2}{c}\\&=& \dfrac{456^2}{753}\\&\approx & 276{,}14\, cm\end{array}$

Berechne $p$
$\begin{array}{rclcc}c &=& q+p &\vert & -q\\p &=& c-q \\&\approx& 753-276{,}14\\&\approx& 476{,}86\,cm\end{array}$

Berechne $h$ mit dem Satz des Pythagoras im rechten Teildreieck
$\begin{array}{rclcc}a^2 &=& h^2+p^2 &\vert &-p^2\\h^2 &=& a^2-p^2 &\vert &\sqrt{}\\h &=& \sqrt{a^2-p^2}\\&\approx& \sqrt{599{,}23^2-476{,}86^2}\\&\approx & 362{,}88\, cm\end{array}$

15)
Berechne $b$ mit dem Satz des Pythagoras im linken Teildreieck
$\begin{array}{rclcc}b^2 &=& h^2+q^2 &\vert &\sqrt{}\\b &=& \sqrt{h^2+q^2}\\&=& \sqrt{20^2+5^2}\\&\approx & 20{,}62\, cm\end{array}$

Berechne $p$ mit dem Höhensatz
$\begin{array}{rclcc}h^2 &=& p\cdot q &\vert &:q\\p &=& \dfrac{h^2}{q}\\&=& \dfrac{20^2}{5}\\&=& 80\, cm\end{array}$

Berechne $c$
$\begin{array}{rclcc}c &=& q+p \\&=& 5+80\\&=& 85\, cm\end{array}$

Berechne $a$ mit einem der Kathetensätze
$\begin{array}{rclcc}a^2 &=& c\cdot p &\vert &\sqrt{}\\a &=& \sqrt{c\cdot p}\\&=& \sqrt{85\cdot 80}\\&\approx & 82{,}46\, cm\end{array}$

6. Aufgabe

1) $d\left(P_1 \mid P_2\right) = \sqrt{(3-1)^2+(3-2)^2} = \sqrt{5} \approx 2{,}24$

2) $d\left(P_1 \mid P_2\right) = \sqrt{\left(-\dfrac{2}{3}-\dfrac{1}{3}\right)^2+(7-2)^2} = \sqrt{26} \approx 5{,}10$

3) $d\left(P_1 \mid P_2\right) = \sqrt{\left(-\dfrac{1}{10}-25\right)^2+(2-(-50))^2} = \sqrt{3.334{,}01} \approx 57{,}74$

4) $d\left(P_1 \mid P_2\right) = \sqrt{\left(-\dfrac{11}{600}-\left(-\dfrac{1}{300}\right)\right)^2+\left(-\dfrac{8}{21}-\dfrac{3}{7}\right)^2} \approx 0{,}81$

5) $d\left(P_1 \mid P_2\right) = \sqrt{(21-7)^2+(22-5)^2} = \sqrt{485} \approx 22{,}02$

6) $d\left(P_1 \mid P_2\right) = \sqrt{\left(\dfrac{1}{2}-(-0{,}5)\right)^2+\left(-\dfrac{31}{4}-7{,}75\right)^2} = \sqrt{241{,}25} \approx 15{,}53$

7) $d\left(P_1 \mid P_2\right) = \sqrt{(3-0)^2+(4-0)^2} = 5$

8) $d\left(P_1 \mid P_2\right) = \sqrt{\left(\dfrac{1}{4}-\dfrac{7}{8}\right)^2+\left(\dfrac{3}{8}-\left(-\dfrac{9}{4}\right)\right)^2} = \sqrt{\dfrac{233}{32}} \approx 2{,}7$

9) $d\left(P_1 \mid P_2\right) = \sqrt{(-83-(-90))^2+(-101-(-23))^2} = \sqrt{6133} \approx 78{,}31$

10) $d\left(P_1 \mid P_2\right) = \sqrt{(33-333)^2+(11-111)^2} = \sqrt{100.000} \approx 316{,}23$

7. Aufgabe

Um die Frage beantworten zu können, muss jeweils geprüft werden, ob die Summe der gegebenen Winkel die Winkelsumme von $180^\circ$ bzw. $\pi$ für ein Dreieck oder $360^\circ$ bzw. $2\pi$ für ein Viereck bereits übersteigt. Dazu müssen die gegebenen Winkel entweder ins Gradmaß oder ins Bogenmaß umgerechnet werden.

1)
 $\begin{array}{rcl} \alpha + \beta &=& \dfrac{\pi}{2}+100^\circ \cr \alpha + \beta &=& 90^\circ+100^\circ \cr \alpha + \beta &=& 190^\circ \cr \alpha + \beta &>& 180^\circ \end{array}$

Es kann kein Dreieck mit diesen Winkeln geben.

2)
$\begin{array}{rcl} \alpha + \gamma &=& 100^\circ + \dfrac{\pi}{4} \cr \alpha + \gamma &=& 100^\circ + 45^\circ \cr \alpha + \gamma &=& 145^\circ \cr \alpha + \gamma & < & 180^\circ \end{array}$

Es kann ein Dreieck mit diesen Winkeln geben.

3)
$\begin{array}{rcl} \alpha + \beta &=& 120^\circ+\dfrac{ \pi}{6} \cr\cr \alpha + \beta &=& \dfrac{2\pi}{3}+\dfrac{ \pi}{6} \cr\cr \alpha + \beta &=& \dfrac{5 \pi}{6} \cr\cr \alpha + \beta & < & \pi \end{array}$

Es kann ein Dreieck mit diesen Winkeln geben.

4)
$\begin{array}{rcl} \beta + \gamma &=& \dfrac{3 \pi}{5}+80^\circ \cr \beta + \gamma &=& 108^\circ+80^\circ \cr \beta + \gamma &=& 188^\circ \cr \beta + \gamma &>& 180^\circ \end{array}$

Es kann kein Dreieck mit diesen Winkeln geben.

5)
$\begin{array}{rcl} \beta + \gamma &=& \pi+18^\circ \cr\cr \beta + \gamma &=& \pi+\dfrac{\pi}{10} \cr\cr \beta + \gamma &=& \dfrac{11 \pi}{10} \cr\cr \beta + \gamma &>& \pi \end{array}$

Es kann kein Dreieck mit diesen Winkeln geben.

6)
$\begin{array}{rcl}\alpha + \beta &=& \dfrac{\pi}{10}+145^\circ \\\alpha + \beta &=& 18^\circ +145^\circ \\\alpha + \beta &=& 163^\circ \\\alpha + \beta & < & 180^\circ \\\end{array}$

Es kann ein Dreieck mit diesen Winkeln geben.

7)
$\begin{array}{rcl}\beta + \gamma &=& 10^\circ +\dfrac{5\pi}{4} \\\beta + \gamma &=& 10^\circ +225^\circ \\\beta + \gamma &=& 235^\circ \\\beta + \gamma &>& 180^\circ \\\end{array}$

Es kann kein Dreieck mit diesen Winkeln geben.

8)
$\begin{array}{rcl}\alpha + \beta &=& 30^\circ+\dfrac{\pi}{3} \\\\\alpha + \beta &=& \dfrac{\pi}{6} +\dfrac{\pi}{3} \\\\\alpha + \beta &=& \dfrac{\pi}{2} \\\\\alpha + \beta & < & \pi \\\end{array}$

Es kann ein Dreieck mit diesen Winkeln geben.

9)
$\begin{array}{rcl}\alpha + \beta &=& \dfrac{3\pi}{8}+45^\circ \\\alpha + \beta &=& 67{,}5^\circ +45^\circ \\\alpha + \beta &=& 112{,}5^\circ \\\alpha + \beta & < & 180^\circ \\\end{array}$

Es kann ein Dreieck mit diesen Winkeln geben.

10)
$\begin{array}{rcl}\alpha + \gamma &=& 1{,}8^\circ+\dfrac{99\pi}{100} \\\\\alpha + \gamma &=& \dfrac{\pi}{100} +\dfrac{99\pi}{100} \\\\\alpha + \gamma &=& \pi \\\end{array}$

Es kann kein Dreieck mit diesen Winkeln geben.

11)
$\begin{array}{rcl}\alpha + \beta + \gamma &=& \dfrac{5\pi}{6}+30^\circ +60^\circ \\\alpha + \beta + \gamma &=& 150^\circ +30^\circ +60^\circ \\\alpha + \beta + \gamma &=& 240^\circ \\\alpha + \beta + \gamma & < & 360^\circ \\\end{array}$

Es kann ein Viereck mit diesen Winkeln geben.

12)
$\begin{array}{rcl}\alpha + \beta + \gamma &=& 45^\circ +\dfrac{3\pi}{2} +\dfrac{\pi}{4} \\\\\alpha + \beta + \gamma &=& \dfrac{\pi}{4} +\dfrac{3\pi}{2} +\dfrac{\pi}{4} \\\\\alpha + \beta + \gamma &=& 2\pi \\\end{array}$

Es kann kein Viereck mit diesen Winkeln geben.

13)
$\begin{array}{rcl}\alpha + \beta + \gamma &=& \dfrac{\pi}{9} +180^\circ +10^\circ \\\\\alpha + \beta + \gamma &=& \dfrac{\pi}{9} +\pi +\dfrac{\pi}{18} \\\\\alpha + \beta + \gamma &=& \dfrac{7\pi}{6} \\\\\alpha + \beta + \gamma & < & 2\pi \\\end{array}$

Es kann ein Viereck mit diesen Winkeln geben.

14)
$\begin{array}{rcl}\alpha + \beta + \gamma &=& \dfrac{9\pi}{8} +30^\circ +\dfrac{2\pi}{5} \\\\\alpha + \beta + \gamma &=& \dfrac{9\pi}{8} +\dfrac{\pi}{6} +\dfrac{2\pi}{5} \\\\\alpha + \beta + \gamma &=& \dfrac{203\pi}{120} \\\alpha + \beta + \gamma & < & 2\pi\\\end{array}$

Es kann ein Viereck mit diesen Winkeln geben.

15)
$\begin{array}{rcl}\alpha + \beta + \gamma &=& \dfrac{11\pi}{18} +70^\circ +\dfrac{17\pi}{18} \\\alpha + \beta + \gamma &=& 110^\circ +70^\circ +170^\circ \\\alpha + \beta + \gamma &=& 350^\circ \\\alpha + \beta + \gamma & < & 360^\circ \\\end{array}$

Es kann ein Viereck mit diesen Winkeln geben.

16)
$\begin{array}{rcl}\alpha + \beta + \gamma &=& \dfrac{2\pi}{3} +\dfrac{\pi}{6} +\pi \\\alpha + \beta + \gamma &=& 120^\circ +30^\circ +180^\circ \\\alpha + \beta + \gamma &=& 330^\circ \\\alpha + \beta + \gamma & < & 360^\circ \\\end{array}$

Es kann ein Viereck mit diesen Winkeln geben.

17)
$\begin{array}{rcl}\alpha + \beta + \gamma &=& 32^\circ +\dfrac{6\pi}{5} +\dfrac{23\pi}{36} \\\alpha + \beta + \gamma &=& 32^\circ +216^\circ +115^\circ \\\alpha + \beta + \gamma &=& 363^\circ \\\alpha + \beta + \gamma &>& 360^\circ \\\end{array}$

Es kann kein Viereck mit diesen Winkeln geben.

18)
$\begin{array}{rcl}\alpha + \beta + \gamma &=& 5^\circ +5^\circ +0{,}1\pi \\\alpha + \beta + \gamma &=& 5^\circ +5^\circ +18^\circ \\\alpha + \beta + \gamma &=& 28^\circ \\\alpha + \beta + \gamma & < & 360^\circ \\\end{array}$

Es kann ein Viereck mit diesen Winkeln geben.

19)

$\begin{array}{rcl}\alpha + \beta + \gamma &=& \dfrac{\pi}{2} +120^\circ +180^\circ \\\alpha + \beta + \gamma &=& 90^\circ +120^\circ +180^\circ \\\alpha + \beta + \gamma &=& 390^\circ \\\alpha + \beta + \gamma &>& 360^\circ \\\end{array}$

Es kann kein Viereck mit diesen Winkeln geben.

20)
$\begin{array}{rcl}\alpha + \beta + \gamma &=& \dfrac{5\pi}{4} +90^\circ +\dfrac{7\pi}{12} \\\alpha + \beta + \gamma &=& 225^\circ +90^\circ +105^\circ \\\alpha + \beta + \gamma &=& 420^\circ \\\alpha + \beta + \gamma &>& 360^\circ \\\end{array}$

Es kann kein Viereck mit diesen Winkeln geben.

8. Aufgabe

Bemerkung: In der Mathematik ist es - anders als in der Physik - üblich, die Einheiten während der Rechnung nicht hinzuschreiben. Erst im Antwortsatz, der bei Textaufgaben dazugehört, muss die Einheit notiert werden.

Sei $x \in \mathbb{N}$ die Anzahl der angefangenen Quadratmeter.

Zuerst berechnen wir die Anzahl der Quadratmeter, die mit $1000\, \text{EUR}$ maximal möglich sind (Für das Lösen der Ungleichung kann Kapitel 18 helfen ...):
$\begin{array}{rclcl} 1000 &\geq& 250+60x &\vert& - 250 \cr 750 &\geq& 60x &\vert& :60 \cr 12{,}5 &\geq& x \end{array}$

Da $x$ eine ganze Zahl ist, müssen wir abrunden: $x=12 m^2$.

Nun berechnen wir die zweite Seite $b$ bei einer maximalen Fläche $A=12 \, m^2$.

$\begin{array}{rcl} A &=& a\cdot b \cr 12 &=& 5 \cdot b \cr b &=& \dfrac{12}{5} \cr b &=& 2{,}4 \end{array}$

Die zweite Seite der Terrasse kann also maximal $2{,}4\,m$ lang werden.

9. Aufgabe

Bemerkung: Statt Ober- und Mantelfläche separat anhand der Formeln zu berechnen, kann man auch erst die Mantelfläche bestimmen und anschließend die Grund- und ggf. die Deckflächen addieren.

1)
$\begin{array}{rcl} V &=& a^3 \cr V &=& (16 \, cm)^3 \cr V&=&4.096 \, cm^3 \end{array}$

2)
Achtung: Einheiten umrechnen!

$\begin{array}{rcl} V &=& ab c \cr V &=& 3{,}5 \, cm\cdot 5{,}5 \, cm \cdot 11 \, cm \cr V &=& 211{,}75 \, cm^3 \end{array}$

3)
$\begin{array}{rcl} V &=& \pi r^2 h \cr V &=& \pi \cdot (7{,}5 \, m)^2 \cdot10 \, m \cr V &\approx& 1.767{,}15 \, m^3\end{array}$

4)
$\begin{array}{rcl} V &=& \dfrac{1}{3} a^2 h \cr V &=& \dfrac{1}{3}\cdot (7 \, m)^2\cdot 5 \, m \cr V &\approx& 81{,}67 m^3\end{array}$

5)
$\begin{array}{rcl} V &=& \dfrac{1}{3}\pi r^2 h \cr V &=& \dfrac{1}{3}\pi\cdot (14 \, cm)^2 \cdot 31 \, cm \cr V &\approx& 6.362{,}77 \, cm^3 \end{array}$

6)
$\begin{array}{rcl} V &=& \dfrac{4}{3}\pi \left(\dfrac{d}{2}\right)^3 \cr V &=& \dfrac{4}{3}\pi \cdot\left(\dfrac{6{,}7}{2} \, cm\right)^3 \cr V &\approx& 157{,}48 \, cm^3 \end{array}$

$\begin{array}{rcl} A_O &=& 4\pi \left(\dfrac{d}{2}\right)^2 \cr A_O &=& 4\pi \cdot \left(\dfrac{6{,}7}{2} \, cm\right)^2 \cr A_O &\approx& 141{,}03 \, cm^2 \end{array}$

10. Aufgabe

Bemerkung: In der Mathematik ist es - anders als in der Physik - üblich, die Einheiten während der Rechnung nicht hinzuschreiben. Erst im Antwortsatz, der bei Textaufgaben dazugehört, muss die Einheit notiert werden.

1)
Es gilt (Satz des Pythagoras): $a^2 + a^2=d^2$ , wobei mit $a$ die Seiten und mit $d$ die Diagonale des Quadrats bezeichnet wurden (siehe Bemerkung zu Textaufgaben).

Gelöst werden muss also:
$\begin{array}{rclcc} d^2 &=& a^2+a^2 \cr &=& 2a^2 &\vert& \sqrt{} \cr d &=& \sqrt{2a^2} \cr &=& a\cdot\sqrt{2} &\vert& : \sqrt{2} \cr \dfrac{d}{\sqrt{2}} &=& a \cr \cr a &=& \dfrac{5{,}657}{\sqrt{2}} \cr &\approx& 4\end{array}$

Die Seiten des Quadrats sind jeweils ca. $4 \, cm$ lang.

2)
Unter der Raumdiagonale eines Würfels versteht man z. B. die Strecke von der vorderen, linken, unteren Ecke zur hinteren, rechten, oberen.

Es gilt (Satz des Pythagoras): $a^2 + a^2 + a^2=d^2$ , wobei mit $a$ die Seiten und mit $d$ die Diagonale des Würfels bezeichnet wurden.

Gelöst werden muss also:
$\begin{array}{rclcc} d^2 &=& a^2+a^2+a^2 \cr &=& 3a^2 &\vert& \sqrt{} \cr d &=& \sqrt{3a^2} \cr &=& a\cdot\sqrt{3} &\vert& : \sqrt{3} \cr \dfrac{d}{\sqrt{3}} &=& a \cr \cr a &=& \dfrac{17{,}321}{\sqrt{3}} \cr &\approx& 10 \end{array}$

Die Kanten des Würfels sind jeweils ca. $10 \, cm$ lang.

3)
Sei $r$ der Radius der Kugel. Dann gilt für die Oberfläche der Kugel: $O=4\pi r^2$

Also in diesem Fall:
$\begin{array}{rclcl} 615{,}75 &=& 4\pi r^2 &\vert& :\left(4\pi\right) \cr \dfrac{615{,}75}{4\pi} &=& r^2 &\vert& \sqrt{} \cr r &=& \sqrt{\dfrac{615{,}75}{4\pi}} \cr &\approx& 7{,}00 \, cm\end{array}$

Für das Volumen einer Kugel gilt: $V=\dfrac{4}{3}\pi r^3$

Setzt man den eben berechneten Radius in die Volumenformel ein, erhält man:
$\begin{array}{rcl} V &\approx& \dfrac{4}{3}\pi \cdot 7{,}00^3 \cr &=& 1.436{,}76 \end{array}$

Das Volumen der Kugel beträgt ca. $1.436{,}76 \, cm^3$.

11. Aufgabe

Bemerkung: In der Mathematik ist es - anders als in der Physik - üblich, die Einheiten während der Rechnung nicht hinzuschreiben. Erst im Antwortsatz, der bei Textaufgaben dazugehört, muss die Einheit notiert werden.

1)
Auch hier macht sich eine Skizze gut: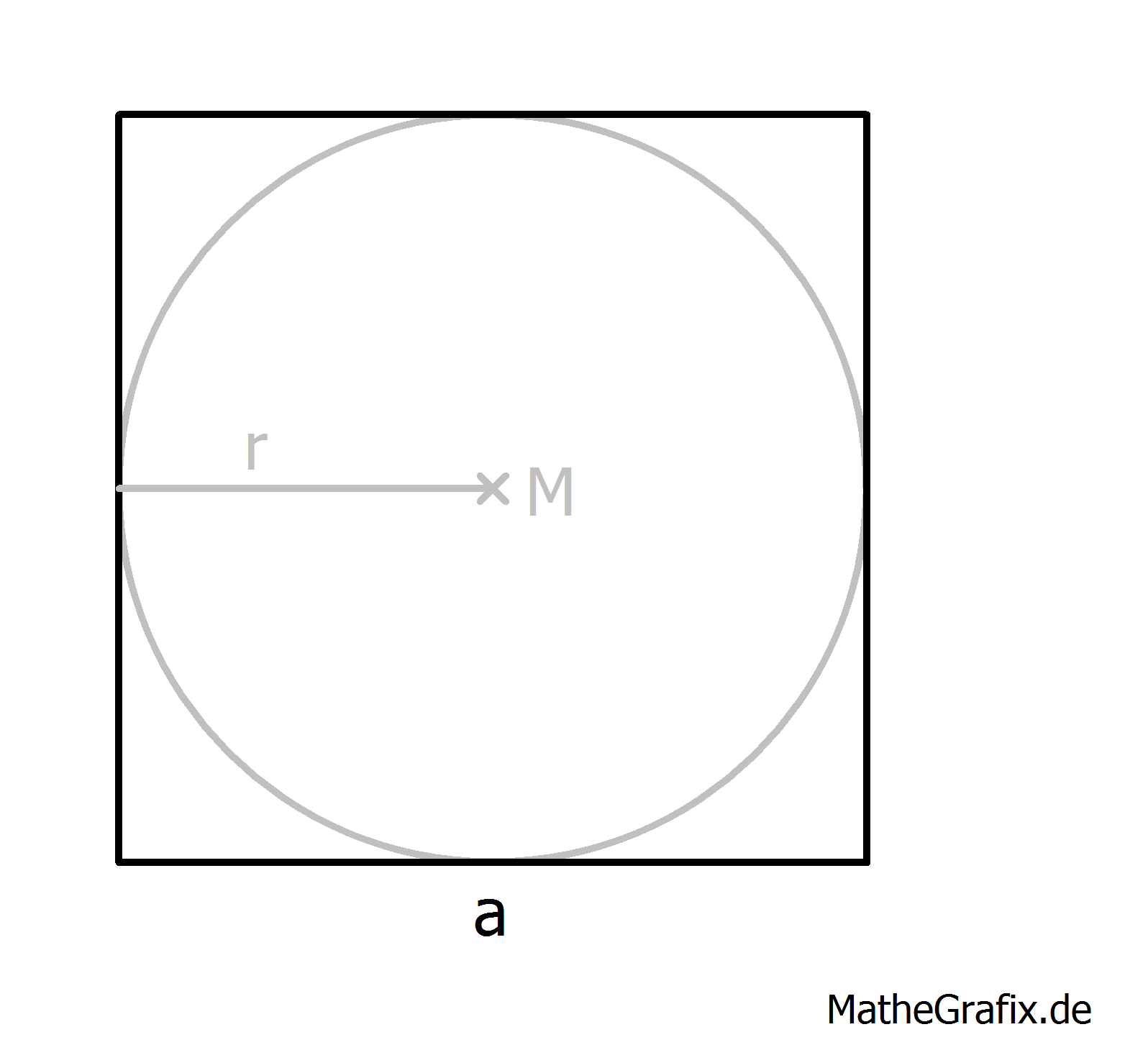

Fläche des Quadrats: $A_Q = a^2$
Radius des Kreises (entspricht der halben Seitenlänge des Quadrats): $r = \dfrac{a}{2}$
Fläche des Kreises: $A_K = \pi r^2 = \pi \left(\dfrac{a}{2}\right)^2 = \dfrac{1}{4}\pi a^2$

Verhältnis Kreisfläche zu Quadratfläche:
$\genfrac{}{}{1pt}{0}{\dfrac{1}{4}\pi a^2}{a^2} = \dfrac{1}{4}\pi$

Das Verhältnis der Kreisfläche zur Quadratfläche beträgt $\dfrac{\pi}{4} \approx 0{,}79$.
Zur Plausibilisierung: Da die Kreisfläche offensichtlich kleiner ist als die Quadratfläche, muss das Ergebnis kleiner als $1$ sein. Passt!

2)
Zunächst eine Skizze:

Fläche des Quadrats: $A_Q = a^2$
Radius des Kreises (entspricht dem halben Durchmesser des Quadrats): $r = \dfrac{1}{2}\sqrt{a^2+a^2}=\dfrac{1}{2}\sqrt{2}\cdot a$
Fläche des Kreises: $A_K = \pi r^2 = \pi \left(\dfrac{1}{2}\sqrt{2}\cdot a\right)^2 = \dfrac{1}{2}\pi a^2$

Verhältnis Kreisfläche zu Quadratfläche:
$\genfrac{}{}{1pt}{0}{\dfrac{1}{2}\pi a^2}{a^2} = \dfrac{1}{2}\pi$

Das Verhältnis der Kreisfläche zur Quadratfläche beträgt $\dfrac{\pi}{2} \approx 1,57$.
Zur Plausibilisierung: Da die Kreisfläche offensichtlich größer ist als die Quadratfläche, muss das Ergebnis größer als $1$ sein. Passt!

3)
Bei Körpern im dreidimensionalen Raum ist es mit Skizzen schwierig ... Aber die Zeichnung, die wir für die zweidimensionalen Figuren erstellt haben, helfen für die Anschauung schon ganz gut weiter.

Kugel im Würfel:

Volumen des Würfels mit Kantenlänge $a$: $V_W = a^3$
Radius der Kugel (entspricht der halben Kantenlänge des Würfels): $r = \dfrac{a}{2}$
Volumen der Kugel: $V_K = \dfrac{4}{3}\pi r^3 = \dfrac{4}{3}\pi \left(\dfrac{a}{2}\right)^3 = \dfrac{4}{3}\pi \cdot \dfrac{a^3}{8} =\dfrac{1}{6} \pi a^3$

Verhältnis Kugelvolumen zum Würfelvolumen:
$\genfrac{}{}{1pt}{0}{\dfrac{1}{6} \pi a^3}{a^3} = \dfrac{1}{6}\pi$

Das Verhältnis des Kugelvolumens zum Würfelvolumen beträgt $\dfrac{1}{6}\pi\approx 0{,}52$.
Zur Plausibilisierung: Da das Kugelvolumen offensichtlich kleiner ist als das Würfelvolumen, muss das Ergebnis kleiner als $1$ sein. Passt!

Würfel in Kugel:

Volumen des Würfels mit Kantenlänge $a$: $V_W = a^3$
Radius der Kugel (entspricht der halben Raumdiagonalen des Würfels): $r = \dfrac{1}{2}\sqrt{a^2+a^2+a^2} = \dfrac{\sqrt{3}\cdot a}{2}$
Volumen der Kugel: $V_K = \dfrac{4}{3}\pi r^3 = \dfrac{4}{3}\pi \left(\dfrac{\sqrt{3}\cdot a}{2} \right)^3 = \dfrac{4}{3}\pi \cdot \dfrac{3\sqrt{3}\cdot a^3}{8} = \dfrac{\sqrt{3}}{2}\pi a^3$

Verhältnis Kugelvolumen zum Würfelvolumen:
$\genfrac{}{}{1pt}{0}{\dfrac{\sqrt{3}}{2}\pi a^3}{a^3} = \dfrac{\sqrt{3}}{2}\pi$

Das Verhältnis des Kugelvolumens zum Würfelvolumen beträgt $\dfrac{\sqrt{3}}{2}\pi \approx 2{,}72$.
Zur Plausibilisierung: Da das Kugelvolumen offensichtlich größer ist als das Würfelvolumen, muss das Ergebnis größer als $1$ sein. Passt!

12. Aufgabe

Hinweis: Da $1\, l =1.000 \, cm^3$ ist, ist $0{,}25\,l = 250 cm^3$.

a)
Umstellen der Volumenformel nach $h$
$\begin{array}{rclcl} V &=& \pi r^2 h &\vert& : \pi :r^2 \cr \dfrac{V}{\pi r^2} &=& h \end{array}$

Berechnen der Zylinderoberfläche
$\begin{array}{rcl} A_O &=& 2\pi r(r+h) \cr A_O &=& 2\pi r\left(r+\dfrac{V}{\pi r^2}\right) \cr A_O &=& 2\pi\cdot 3{,}75\, cm \left(3{,}75\, cm+\dfrac{250\, cm^3}{\pi \left(3{,}75\, cm\right)^2}\right) \cr A_O &\approx& 221{,}69 \, cm^2 \end{array}$

Bemerkung: Da wir hier mit dem Radius rechnen, müssen wir den Durchmesser halbieren: $7{,}5 : 2 = 3{,}75$.

b)
Umstellen der Volumenformel nach $c$, wobei $b=2a$
$\begin{array}{rclcl} V &=& a\cdot b\cdot c &\vert& :a:b \cr \dfrac{V}{a\cdot b} &=& c \cr \dfrac{V}{a\cdot 2a} &=& c\end{array}$

Berechnen der Quaderoberfläche
$\begin{array}{rcl} A_O &=& 2(ab+ac+bc) \cr A_O &=& 2\left(ab+a\dfrac{V}{a\cdot 2a}+b\dfrac{V}{a\cdot 2a}\right) \cr A_O &=& 2 \left(4 \, cm \cdot 8 \, cm+4 \, cm \cdot \dfrac{250\, cm^3}{4 \, cm \cdot 8 \, cm}+8 \, cm \cdot \dfrac{250\, cm^3}{4 \, cm \cdot 8 \, cm} \right) \cr A_O &=& 251{,}5 \, cm^2 \end{array}$

c)
Umstellen der Volumenformel nach $a$
$\begin{array}{rclcl} V &=& a^3 &\vert& \sqrt[3]{} \cr \sqrt[3]{V} &=& a \end{array}$

Berechnen der Würfeloberfläche
$\begin{array}{rcl} A_O &=& 6 a^2 \cr A_O &=& 6 \left(\sqrt[3]{V}\right)^2 \cr A_O &=& 6\left(\sqrt[3]{250 \, cm^3}\right)^2 \cr A_O &\approx& 238{,}11\, cm^2 \end{array}$

d)
Umstellen der Volumenformel nach $r$
$\begin{array}{rclcl} V &=& \dfrac{4}{3}\pi r^3 &\vert& :\dfrac{4}{3} : \pi \cr \dfrac{3V}{4\pi} &=& r^3 &\vert& \sqrt[3]{ } \cr \sqrt[3]{\dfrac{3V}{4\pi}} &=& r \end{array}$

Berechnen der Kugeloberfläche
$\begin{array}{rcl} A_O &=& 4\pi r^2 \cr A_O &=& 4\pi\cdot \left(\sqrt[3]{\dfrac{3V}{4\pi}} \right)^2 \cr A_O &=& 4\pi\cdot \left(\sqrt[3]{\dfrac{3\cdot 250\;cm^3}{4\pi}} \right)^2 \cr A_O &\approx& 191{,}92 \, cm^2 \end{array}$

Schlussfolgerung aus a) bis d): Die optimale Alternative ist die Dose in Kugelform, da hier die Oberfläche und damit der Materialverbrauch bei gleichem Volumen am geringsten ist. Da diese sich aber schwer herstellen, transportieren, lagern und im Alltag handhaben lässt, ist diese Lösung für die Praxis nicht geeignet. Die Entscheidung fällt also auf die Dose in Zylinderform.

13. Aufgabe

a)
$\begin{array}{rcl} V &=& \dfrac{1}{4}\pi d^2 \cdot h \cr V &=& \dfrac{1}{4} \pi \cdot (0{,}15 \, m)^2 \cdot 15 \, m \cr V &\approx& 0{,}26507 \,m^3 \end{array}$

Das Rohr fasst ca. $0{,}26507 \,m^3$ bzw. $265{,}07 \,l$.

b)
$\begin{array}{rcl} A_M &=& \pi d \cdot h \cr A_M &=& \pi\cdot 0{,}2\, m \cdot 15\,m \cr A_M &\approx& 9{,}42 \,m^2 \end{array}$

Die Mantelfläche beträgt ca. $9{,}42 \,m^2$.

14. Aufgabe

Gesucht ist das Volumen des Beckens:

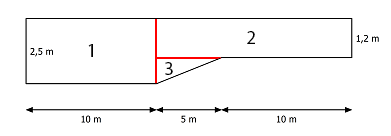
Zunächst zerlegen wir die Seitenfläche $A_G$ in Teilflächen $A_1$, $A_2$ und $A_3$:

Achtung: Da das Becken nur bis $10\,cm$ unter den Rand gefüllt werden soll, muss bei den Teilflächen $A_1$ und $A_2$ mit $2{,}4\,m$ und $1{,}1\,m$ gerechnet werden.

Rechteck $A_1$
$\begin{array}{rcl} A_1 &=& 2{,}4 \, m \cdot 10 \,m \cr A_1 &=& 24 \, m^2 \end{array}$

Rechteck $A_2$
$\begin{array}{rcl} A_2 &=& 1{,}1 \, m \cdot 15 \,m \cr A_2 &=& 16{,}5 \, m^2 \end{array}$

Rechtwinkliges Dreieck $A_3$
$\begin{array}{rcl} A_3 &=& \dfrac{1}{2}\cdot 5\, m \cdot 1{,}3 \,m \cr A_3 &=& 3{,}25 \, m^2 \end{array}$

Daraus berechnen wir die Gesamtfläche $A_G$:
$\begin{array}{rcl} A_G &=& A_1+A_2+A_3 \cr A_G &=& 24 \, m^2+16{,}5 \, m^2+3{,}25 \, m^2 \cr A_G &=& 43{,}75 \,m^2 \end{array}$


Nun berechnen wir das Volumen aus der Gesamtfläche $A_G$ und der Breite des Beckens $b$:
$\begin{array}{rcl} V &=& A_G\cdot b \cr V &=& 43{,}75 \,m^2 \cdot 15\,m \cr V &=& 656{,}25 \,m^3 \end{array}$

Um das Becken mit einem Volumen $656{,}25 \,m^3$ zu füllen, werden $656.250\, l$ Wasser benötigt, da $1\, m^3 = 1.000 \, l$ ist.