Übersicht:

21.1 Trigonometrie - Aufgaben

Bemerkung vorab: Runden Sie bei den folgenden Aufgaben – wenn nötig – auf zwei Stellen nach dem Komma. Wichtig ist, immer erst ganz zum Schluss zu runden, damit die Rundungsfehler nicht zu groß werden!

1. Aufgabe

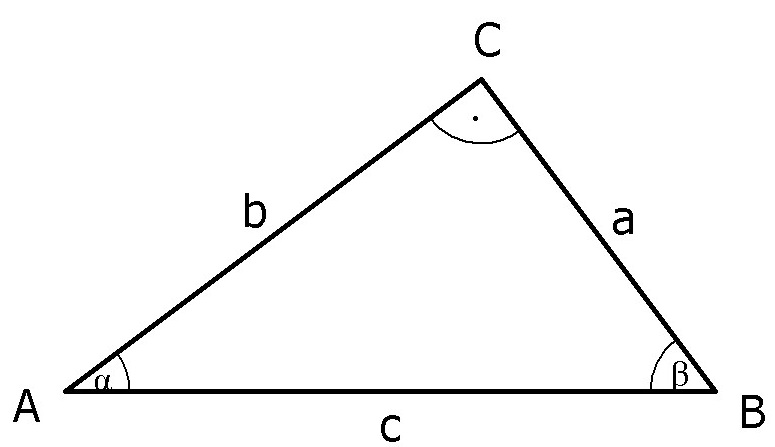
Berechnen Sie aus den gegebenen Werten die fehlenden Seiten und Winkel der Dreiecke! Alle Bezeichnungen beziehen sich auf die unten stehende Zeichnung.

1) $b=4 \, cm$ und $\alpha = \dfrac{11 \pi}{36}$		6) $b=12 \, cm$ und $\beta = \dfrac{\pi}{6}$
2) $c=11 \, cm$ und $\alpha = \dfrac{\pi}{8}$		7) $\alpha = 50^{\circ}$ und $\beta = 40^{\circ}$
3) $a=5 \, cm$ und $b=8 \, cm$		8) $c=5 \, cm$ und $\alpha = 15^{\circ}$
4) $c=6{, }7 \, cm$ und $\beta = \dfrac{3\pi}{5}$		9) $a=13 \, cm$ und $c = 13 \, cm$
5) $b=3 \, cm$ und $c=7{,}5 \, cm$		10) $\beta=36^{\circ}$ und $a = 9{,}3 \, cm$

rechtwinkliges Dreieck mit klassischen Bezeichnungen

2. Aufgabe

In einem Trapez haben die parallelen Seiten die Längen $10 \, cm$ und $4 \, cm$ . Die beiden übrigen Seiten haben die Länge $5 \, cm$ .
Bestimmen Sie die Höhe und alle Winkel!

3. Aufgabe

Zeichnen Sie die folgenden Funktionsgraphen!

1) $f_1(x)=3 \sin(x)+1$		4) $f_4(x)=\tan \left(x-\dfrac{\pi}{2} \right)$
2) $f_2(x)=\cos \left(x+\dfrac{\pi}{2} \right)$		5) $f_5(x)=-2 \cos \left( \dfrac{1}{2}x-\dfrac{\pi}{2} \right)$
3) $f_3(x)=-\sin(2x)$

4. Aufgabe

Berechnen Sie $\sin^2(1^\circ)+\sin^2(2^\circ)+\dots +\sin^2(89^\circ)+\sin^2(90^\circ)$ - OHNE Taschenrechner, Computer, Handy und Co zu benutzen!

5. Aufgabe

Für Profis: Warum gilt $\sin^2(\alpha)+\cos^2(\alpha)=1$ für alle $\alpha\in\mathbb{R}$ ?