SOS Mathematik
Übersicht:
- Lösung zur 1. Aufgabe
- Lösung zur 2. Aufgabe
- Lösung zur 3. Aufgabe
- Lösung zur 4. Aufgabe
- Lösung zur 5. Aufgabe
21.3 Trigonometrie - Lösungen
Eine Bemerkung vorab: Da die Variablen bei diesen Aufgaben alle für geometrische Objekte (meistens Strecken) stehen, dürfen wir davon ausgehen, dass sie eine messbare Länge haben. Beim Umformen der Formeln (z. B. bei Aufgabe 5.1) können eine Division durch oder eine Multiplikation mit also nicht auftreten.
1. Aufgabe
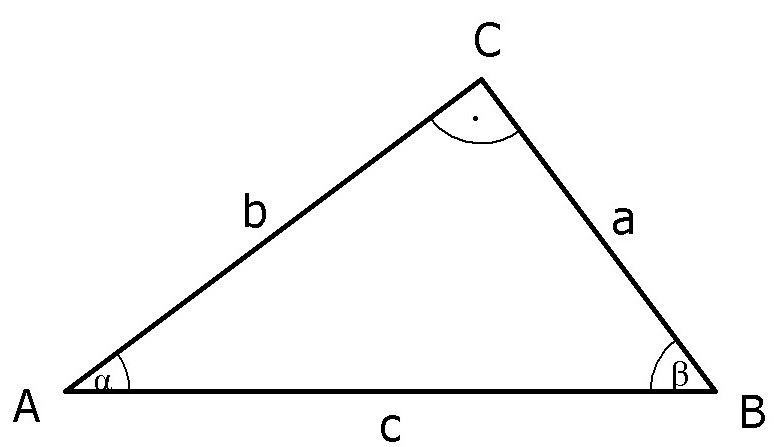
Sehr wichtig: Alle Winkel in dieser Aufgabe sind im Bogenmaß angegeben. Achten Sie also darauf, dass Ihr Taschenrechner entsprechend eingestellt ist!
Bemerkung 1: Bei diesen Aufgaben sind viele verschiedene Lösungswege möglich, z. B. können neben anderen trigonometrischen Funktionen auch der Satz des Pythagoras und der Winkelsummensatz benutzt werden, um die gesuchten Elemente der Dreiecke zu berechnen. Der Einsatz des Winkelsummensatzes hat den Vorteil, dass der Rechenweg schneller und die Ergebnisse genauer sind, als wenn man die trigonometrischen Funktionen nutzt, weil hierbei quasi zwangsläufig Rundungsfehler entstehen.
Bemerkung 2: Um solche Rundungsfehler so klein wie möglich zu halten, sollte - soweit es geht - mit den gegebenen Werte gerechnet werden bzw. nicht zu früh zu stark gerundet werden.
1)
Berechne :
Berechne :
Berechne :
Bemerkung: Wenn Sie und
berechnet haben, ist Ihr Taschenrechner auf Gradmaß eingestellt. Dass diese Ergebnisse nicht richtig sein können, merken Sie daran, dass dann der Satz des Pythagoras nicht gilt:
. Das muss in einem rechtwinkligen Dreieck wie diesem aber so sein.
2)
Berechne :
Berechne :
Berechne :
Bemerkung: Wenn Sie und
berechnet haben, ist Ihr Taschenrechner auf Gradmaß eingestellt. Dass diese Ergebnisse nicht richtig sein können, merken Sie daran, dass man in diesem Fall über die trigonometrischen Funktionen
berechnet, sodass sich für die Winkelsumme
ergibt.
3)
Berechne :
Berechne :
Berechne :
Bemerkung: Wenn Sie berechnet haben, ist Ihr Taschenrechner auf Gradmaß eingestellt.
4)
Berechne :
Bemerkung: Bei diesem Ergebnis sollte man stutzig werden. Es ist rechnerisch korrekt, trotzdem kann offensichtlich etwas nicht stimmen. Schaut man sich die zwei bislang bekannten Winkel an (da wir von einem rechtwinkligen Dreieck ausgehen, ist ), stellt man fest, dass
. Aus den gegebenen Werten lässt sich also gar kein Dreieck konstruieren, da die Summe dieser beiden Winkel bereits die Dreieckswinkelsumme von
überschreitet. Wir brauchen also nicht nicht weiterzurechnen ...
5)
Berechne :
Berechne :
Berechne :
Bemerkung: Wenn Sie berechnet haben, ist Ihr Taschenrechner auf Gradmaß eingestellt.
6)
Berechne :
Berechne :
Berechne :
Bemerkung: Wenn Sie und
berechnet haben, ist Ihr Taschenrechner auf Gradmaß eingestellt.
7)
Bei diesen Angaben können die Seitenlängen nicht berechnet werden, da dafür mindestens eine Seite gegeben sein müsste.
8)
Berechne :
Berechne :
Berechne :
Bemerkung: Wenn Sie und
berechnet haben, ist Ihr Taschenrechner auf Bogenmaß eingestellt. Dass diese Ergebnisse nicht richtig sein können, sollte offensichtlich sein.
9)
Aus diesen Werten ergibt sich kein Dreieck, weil die Hypotenuse immer länger sein muss als die Katheten.
10)
Berechne :
Berechne :
Berechne :
Bemerkung: Wenn Sie und
berechnet haben, ist Ihr Taschenrechner auf Bogenmaß eingestellt.
2. Aufgabe
In der Mathematik ist es - anders als in der Physik - üblich, die Einheiten während der Rechnung nicht hinzuschreiben. Erst im Antwortsatz, der bei Textaufgaben dazugehört, muss die Einheit notiert werden.
Für solche Aufgaben sollte man immer eine Skizze anfertigen: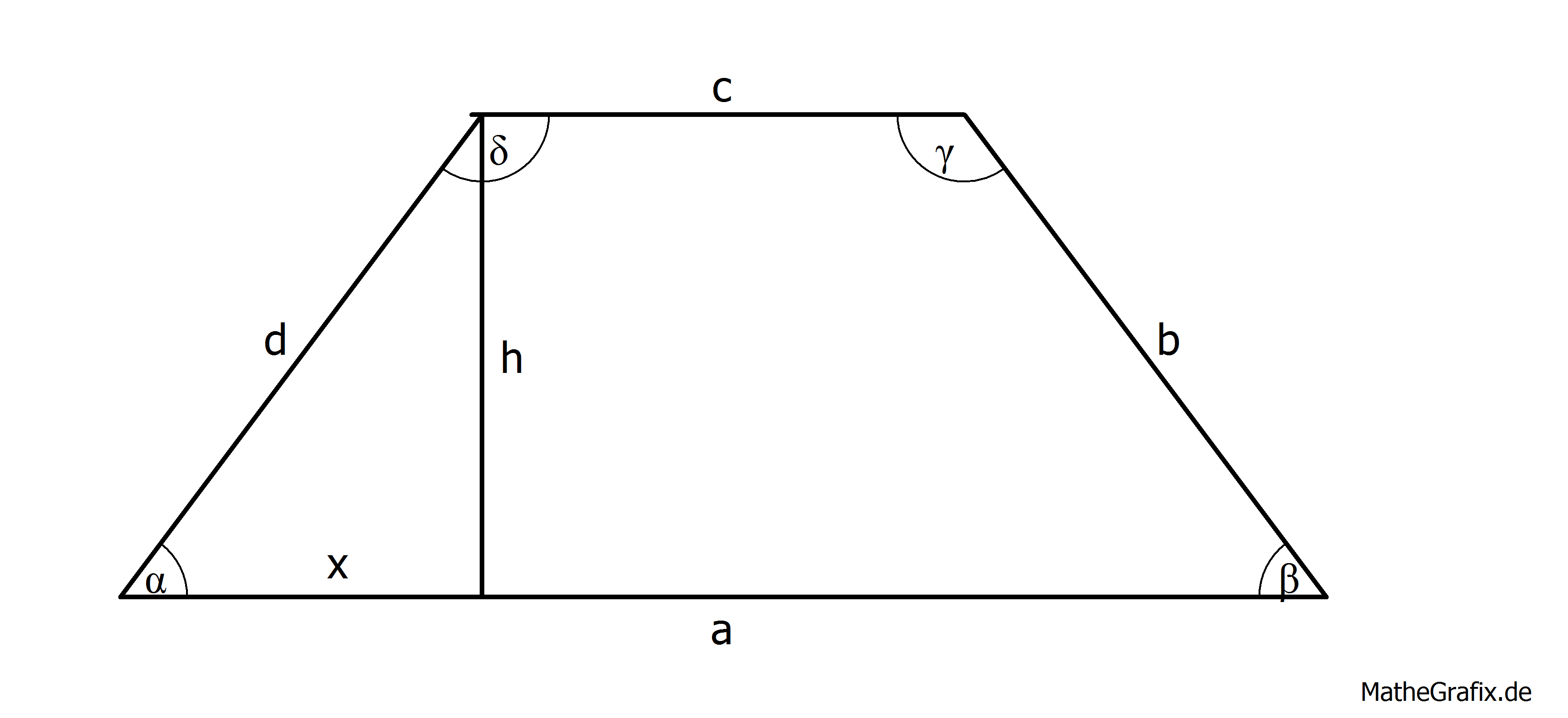
Gegeben sind die Seiten ,
und
.
Die Höhe ist der Abstand der parallelen Seiten. Um sie mittels des Satzes des Pythagoras zu berechnen, benötigen wir die Länge der Strecke
. Da das Trapez symmetrisch ist, ist
genauso halb so lang, wie der Unterschied zwischen der unteren und der oberen Seite des Trapezes:
. Dann berechnet man:
Für die Berechnung der Winkel nutzt man den Sinus und den Winkelsummensatz für Vierecke:
Aufgrund der Symmetrie muss dann auch sein.
Ergebnisse:
Die Höhe des Trapezes ist
lang.
Die Winkel und
haben jeweils eine Größe von
und
und
von je
.
3. Aufgabe
Einige Überlegungen zu dieser Aufgabe:
- Der grundsätzliche Lösungsweg ist ähnlich zu dem, der für Parabeln beschrieben wurde, d. h. Summanden oder Faktoren an den entsprechenden Stellen habe auf trigonometrische Funktionen die gleiche Wirkung wie auf Parabeln.
- Nützlich ist zudem, sich zu überlegen, wo Nullstellen, Minima, Maxima und Polstellen der modifizierten Sinus-, Kosinus- und Tangenskurven liegen bzw. wie sich die Funktionswerte der Minima und Maxima sowie die Periodenlänge verändern. Man kommt zu Überlegungen derart:
hat bei
ein Maximum mit
. Folglich muss
ebenfalls bei
ein Maximum haben, denn
hat eine Periodenlänge von
. Folglich muss auch
eine Periodenlänge von
haben, da die Funktion nicht gestaucht oder gestreckt, sondern nur verschoben wurde.
hat bei
eine Nullstelle. Folglich muss
ebenfalls bei
eine Nullstelle haben, denn
.
hat bei
eine Polstelle. Folglich muss
bei
eine Polstelle haben, denn
.
- Grundsätzlich kann beim Zeichnen von Funktionsgraphen eine Wertetabelle helfen.
Der Übersichtlichkeit wegen wurden die Funktionsgraphen in zwei Koordinatensysteme gezeichnet.
1)
2)
3)
4)
5)
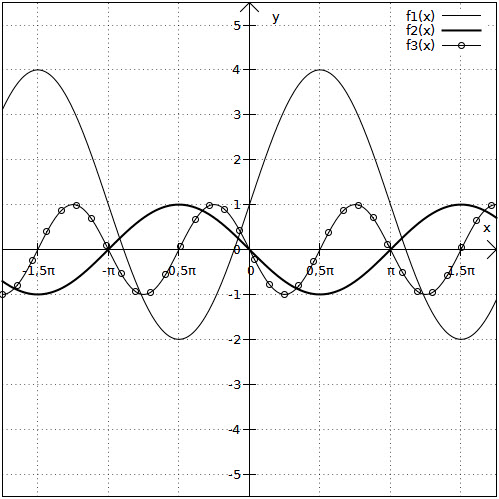
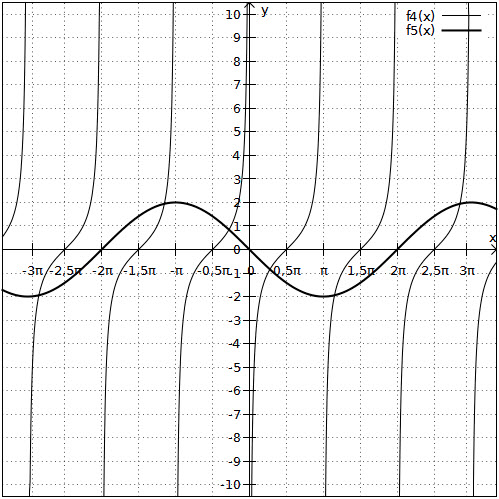
4. Aufgabe
Die Erklärungen zu den einzelnen Umformungsschritten folgen am Ende. Rechnen wir also los:
1. Zeile: Hier wurden nur die Summanden ein bisschen umsortiert.
2. Zeile: Da sich Sinus und Kosinus nur durch eine Verschiebung um unterscheiden, gilt
. Das bedeutet z. B., dass
ist.
3. Zeile: In Kombination mit dem trigonometrischen Pythagoras ergibt sich daraus
.
Danach müssen wir nur noch ausrechnen ...
5. Aufgabe
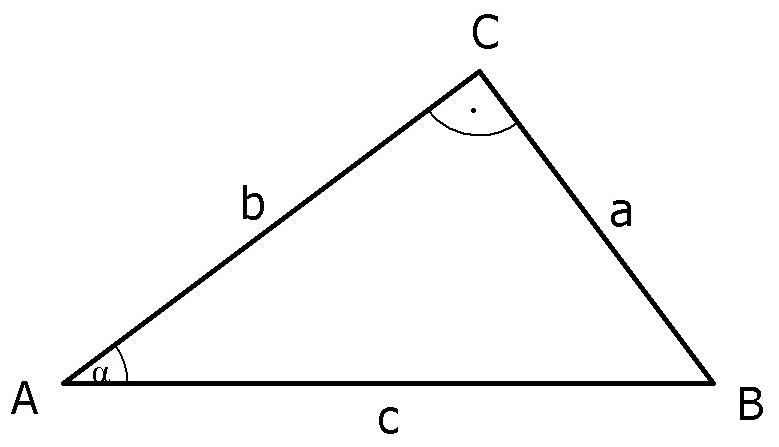
Mit den Bezeichnungen an diesem Dreieck gilt nach den Definitionen für Sinus und Kosinus:
Nach dem Satz des Pythagoras gilt:
Setzt man in diese Gleichung die oben gefundenen Ausdrücke für die Seiten und
ein, erhält man:
Bemerkung 1: steht für
und nicht für
Bemerkung 2: Es darf hier durch geteilt werden, weil die Länge der Hypotenuse immer größer als
ist - sonst wäre es ja kein Dreieck.