Dieses Kapitel enthält die folgenden Themen:

• Definition
• Logarithmusgleichungen
• Logarithmusfunktionen

17.2 Logarithmusgleichungen und -funktionen - Erklärungen

Zu guter Letzt bleiben aus dem Kapitel Potenzen, Wurzeln, Logarithmen noch die Logarithmen. Auch sie dürfen natürlich Bestandteil von Gleichungen und Funktionen sein. Logarithmische Zusammenhänge tauchen in verschiedenen Kontexten auf: Beispielsweise sind die Richterskala, auf der die Stärke von Erdbeben eingeordnet wird, und die Dezibel-Skala zum Abbilden von Lautstärken ebenso logarithmisch wie der pH-Wert. Für uns werden Anwendungen in der Zinsrechnung am relevantesten sein.
Wie der Name schon sagt: Wer sich (noch) nicht mit den Rechenregeln für Logarithmen vertraut gemacht hat, sollte dies nun nachholen. Ebenso hilft ein systematisches und umfassendes Verständnis der Potenzgesetze. Wir werden diese Rechenregeln und -gesetze im nun folgenden Kapitel brauchen.

Definition

Definition einer Logarithmusgleichung: Logarithmusgleichungen sind Gleichungen, bei denen die Variable im Argument eines Logarithmus steht.
Definition einer Logarithmusfunktion: Logarithmusfunktionen sind Funktionen, bei denen die Variable im Argument eines Logarithmus steht.
Anders formuliert: Eine Logarithmusfunktion ist eine Funktion, die jeder Zahl ihren Logarithmus zu einer festen Basis $a\in\mathbb{R}^+\setminus{_{\{1\}}}$ zuordnet.

Exkurs zur Basis: $1$ ist nie Basis einer Logarithmusgleichung oder -funktion. Der Logarithmus beantwortet ja die Frage, wie oft die Basis mit sich selbst multipliziert werden muss, damit das Ergebnis ein bestimmter Wert ist. Bei der Basis $1$ gibt es darauf keine vernünftige Antwort, da $1^x = 1$, egal welchen Wert $x$ hat. Auf die Frage, wie oft $1$ mit sich selbst multipliziert werden muss, damit das Ergebnis $1$ ist, gibt es unendlich viele Lösungen. Auf die Frage, wie oft $1$ mit sich selbst multipliziert werden muss, damit das Ergebnis z. B. $-1$ oder $2$ ist, gibt es keine Lösungen. Das ist keine sinnvolle Grundlage für eine Gleichung/Funktion.
Aus quasi dem gleichen Grund ist $0$ als Basis einer Logarithmusgleichung/-funktion nicht zugelassen.

Definitionsbereich: Auch bei dieser Art von Gleichung ist es wichtig, sich Gedanken zum Definitionsbereich zu machen, da das Argument ja niemals $0$ oder negativ sein darf. Wir müssen also prüfen, für welche Variablenwerte das passiert, und den Definitionsbereich so "zuschneiden", dass nur passende Werte enthalten sind. Dafür müssen wir wieder Ungleichungen lösen.

Logarithmusgleichungen

Schauen wir uns einige Beispiele für Logarithmusgleichungen an:

• $\ln\left(\dfrac{1}{5}x-25\right) = 97$ mit $\mathbb{D} = \left]125;\infty\right[$
  
  
• $-34\log_6\left(a^2-12a+53\right) = 0$ mit $\mathbb{D} = \mathbb{R}$
  
  
• $\ln(e) = -\ln(17)x$ mit $\mathbb{D} = \mathbb{R}$
  Achtung: Diese Gleichung sieht nur aus wie eine Logarithmusgleichung, da in den Argumenten nur Zahlen stehen: $\ln(e) = 1$ (Das ist wichtig zu wissen!) und $-\ln(17) \approx -2{,}83$ (Das kann aber auch einfach als $-\ln(17)$ stehen bleiben.). Da die Variable $x$ außerhalb des Arguments steht und ansonsten nur Zahlen in der Gleichung enthalten sind, haben wir es hier also nur mit der linearen Gleichung $1 = -\ln(17)\cdot x$ zu tun. 

Lösungsweg

Wie bei allen Gleichungstypen, die wir bislang in diesem Lernmodul besprochen haben, ist es auch bei Logarithmusgleichungen das Ziel, die Gleichung so umzuformen, dass etwas entsteht, womit wir schon umgehen können, am liebsten also eine Polynomgleichung. Das klappt auch recht häufig durch Exponenzieren, sodass etliche Logarithmusgleichungen nur auf den ersten Blick wirklich schwierig sind. Grundsätzlich ist es eine gute Idee, die Bestandteile der Gleichung zunächst so weit wie möglich zusammenzufassen. Dabei helfen u. a. die Potenz- und Logarithmengesetze.
Zum Abschluss des Lösungsweges muss - wie schon bei den Bruchgleichungen - noch zwingend überprüft werden, ob sich alle ermittelten Werte für die Variable im Definitionsbereich befinden. Werte, die nicht im Definitionsbereich liegen, stellen keine Lösungen für die ursprüngliche Gleichung dar. Man bezeichnet sie daher als Scheinlösungen. Wie es dazu kommt, wird weiter unten erklärt.
Wie bei Exponentialgleichungen gibt es auch Logarithmusgleichungen, für die sich keine exakten Lösungen finden lassen, sodass man sie nur näherungsweise (also numerisch) lösen kann.

Zur Schreibweise: Mit $e^{*}$ hinter dem senkrechten Strich am Ende einer Zeile ist gemeint, dass beide Seiten der Gleichung die Zahl $e$ als Basis bekommen, also "$e$ hoch" die entsprechenden Terme gerechnet wird; das gilt analog für andere Basen.

Beispiel 1:
Betrachten wir die Gleichung $\ln(2x) = \ln(x+1)$.

Bestimmung des Definitionsbereichs:
Logarithmen sind nur für positive Argumente definiert. Daher müssen wir nun für beide in der Gleichung enthaltenen Logarithmen bestimmen, für welche x-Werte das der Fall ist.
linkes Argument:
$\begin{array}{rclll}2x &>& 0 &\vert & :2\\x &>& 0 \end{array}$

rechtes Argument:
$\begin{array}{rclll}x+1 &>& 0 &\vert & -1 \\x &>& -1\end{array}$

Für die abschließende Ermittlung des Definitionsbereichs bekommen wir also zwei Bedingungen: $x>0$ (für das linke Argument) und $x>-1$ (für das rechte Argument). Da beide Argumente Teil der Gleichung sind, müssen natürlich auch beide Bedingungen erfüllt sein. Dies müssen wir nun prüfen:

• x-Werte kleiner oder gleich $-1$ erfüllen keine Bedingung.
• x-Werte, die größer als $-1$, aber kleiner gleich $0$ sind, erfüllen nur die zweite Bedingung.
  Sie können zur Veranschaulichung einen Wert zwischen $-1$ und $0$ probehalber in den linken Logarithmus einsetzen: Nehmen wir z. B. $-0{,}5$. Das Argument von $\ln\left(2\cdot(-0{,}5)\right) = \ln(-1)$ liegt nicht im zulässigen Bereich. Genau das wollen wir mit der Eingrenzung des Definitionsbereichs ja ausschließen.
• Nur x-Werte größer als $0$ erfüllen beide Bedingungen.

Der Definitionsbereich ist also $\mathbb{D} = ]0;\infty[ = \mathbb{R}^+$.

Lösung der Gleichung:
$\begin{array}{crclcl} \text{1. Zeile:} & \ln(2x) &=& \ln(x+1) &\vert& e^{*} \cr\cr \text{2. Zeile:} & {e^{\ln(2x)}} &=& e^{\ln(x+1)} \cr\cr \text{3. Zeile:} & 2x &=& x+1 &\vert& -x \cr\cr& x &=& 1 \in\mathbb{D} \cr\cr\cr& \mathbb{L} &=& {1}\end{array}$

Zur 1. und 2. Zeile: Die Gleichung wird exponenziert, weil Logarithmieren und Exponenzieren Umkehroperationen sind und sich somit gegenseitig aufheben, wenn die Basen übereinstimmen. Wichtig ist hier (wie bei allen anderen Gleichungstypen), dass solche Umformungen auf beiden Seiten der Gleichung durchgeführt werden.

Ab der 3. Zeile: Nach der ersten Umformung bleibt eine ziemlich simple lineare Gleichung.

Zum Abschluss: Der berechnete Wert liegt im Definitionsbereich und ist also Lösung der Gleichung.

Beispiel 2:
Betrachten wir die Gleichung $\ln(e^x) = \ln(2)+\ln(7)-\ln\left(\dfrac{1}{2}\right)+2\ln\left(2^{-1}\right)$.

Bestimmung des Definitionsbereichs: 
$\begin{array}{rcl}e^x &>& 0\end{array}$

Wir wissen bereits aus dem Kapitel Potenzen, Wurzeln, Logarithmen, dass $e^x$ niemals $0$ oder kleiner sein kann. Insofern ist diese Ungleichung für alle Werte von $x$ erfüllt. Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}$.

Lösung der Gleichung:
$\begin{array}{crclcl}\text{1. Zeile:} & \ln(e^x) &=& \ln(2)+\ln(7)-\ln\left(\dfrac{1}{2}\right)+2\ln\left(2^{-1}\right) \cr\cr \text{2. Zeile:} & x &=& \ln(2)+\ln(7)-\ln\left(\dfrac{1}{2}\right)+2\ln\left(2^{-1}\right) \cr\cr \text{3. Zeile:} & x &=& \ln\left(\frac{2\cdot 7}{\frac{1}{2}}\right)+\ln\left(2^{-2}\right) \cr\cr\text{4. Zeile:} & x &=& \ln\left(2\cdot 7\cdot 2\cdot 2^{-2}\right) \cr\cr & x &=& \ln(7) \in\mathbb{D} \cr\cr\cr& \mathbb{L} &=& \left\{\ln(7)\right\}\end{array}$

Zur 1. Zeile: Da $\ln(x)$ und $e^x$ Umkehroperationen sind, vereinfacht sich die linke Seite der Gleichung sofort zu $x$.

Zur 2. Zeile: Auf der rechten Seite steht gar keine Variable, sodass nur zusammengefasst werden muss. Genutzt werden für die ersten drei Logarithmen das 1. und 2. Logarithmengesetz und für den letzten Logarithmus das 3. Logarithmengesetz.

Zur 3. Zeile: Es wird der Doppelbruch im ersten Logarithmus aufgelöst (Sie wissen ja, multiplizieren mit dem Kehrwert ...) und das 1. Logarithmengesetz erneut angewendet.

Ab der 4. Zeile: Um den Ausdruck auf der rechten Seite weiter zu vereinfachen, werden nun im Argument des Logarithmus die Potenzgesetze angewendet.

Nach Abschluss der Rechnung: Prüfung auf Scheinlösungen!
Wir hatten schon beim Lösen von Bruch- und Wurzelgleichungen gesehen, dass nicht jeder Wert, der berechnet wird, auch tatsächlich Lösung der Ausgangsgleichung sein muss, dass also sogenannte Scheinlösungen auftreten können. Bei Logarithmusgleichung kann das ebenfalls passieren. Schauen wir uns die Gleichung $\ln\left(x\right) = -\ln(4x)$ als Beispiel an:

Bestimmung des Definitionsbereichs:
linkes Argument:
$\begin{array}{rclcl}x &>& 0 \end{array}$

rechtes Argument:
$\begin{array}{rclcl}4x &>& 0 &\vert& :4 \\x &>& 0\end{array}$

Für die abschließende Ermittlung des Definitionsbereichs bekommen wir wieder zwei Bedingungen: Diesmal sind die Bedingungen gleich, nämlich $x>0$. Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}^+$.

Lösung der Gleichung:
$\begin{array}{rclcl}\ln(x) &=& -\ln(4x) &\vert& +\ln(4x) \cr \ln(x)+\ln(4x) &=& 0 &\vert& \text{1. Logarithmengesetz} \cr \ln\left(4x^2\right) &=& 0 &\vert& e^{*} \cr 4x^2 &=& 1 \cr& ... & \cr x_1 &=& \dfrac{1}{2} \cr x_2 &=& -\dfrac{1}{2}\end{array}$

$x_1=\frac{1}{2}$ und $x_2=-\frac{1}{2}$ lösen zwar beide die quadratische Gleichung $4x^2=1$, aber nur $x_1=\frac{1}{2}$ löst auch die ursprüngliche Gleichung $\ln(x)=-\ln(4x)$, weil $x_2=-\frac{1}{2}$ außerhalb des zu Beginn bestimmten Definitionsbereichs $\mathbb{D}=\mathbb{R}^+$ liegt. Setzen wir $x_2=-\frac{1}{2}$ in die Ausgangsgleichung ein, bekommen wir folglich ein Problem:
$\ln\left(-\dfrac{1}{2}\right) = -\ln\left(4\cdot\left(-\dfrac{1}{2}\right)\right)$
Das geht nicht, weil der Logarithmus für negative Werte nicht definiert ist! Ursache dafür ist, dass die quadratische Gleichung einen größeren Definitionsbereich hat als die Logarithmusgleichung (bei quadratischen Gleichungen umfasst der Definitionsbereich ja die gesamten reellen Zahlen). Beim Lösen der quadratischen Gleichung erhalten wir einen Wert, der nicht im ursprünglichen Definitionsbereich liegt und müssen diesen aus der Lösungsmenge unserer Beispielgleichung ausschließen. Es ist demnach: $\mathbb{L}=\left\{\dfrac{1}{2}\right\}$
Nach dem Lösen einer Logarithmusgleichung muss also immer geprüft werden, ob der berechnete Wert im Definitionsbereich liegt. Andersfalls handelt es sich um eine Scheinlösung.

Logarithmusfunktionen

Bei den Logarithmusfunktionen betrachten wir - anders als in den Kapiteln zuvor - nur zwei Fälle: einen mit den klassischen Logarithmusfunktionen (die alle eine Basis größer als $1$ haben) und einen mit komplexeren. Logarithmusfunktionen mit Basen zwischen $0$ und $1$ kommen in Anwendungsfälle nicht sehr häufig vor, sodass wir uns hier nicht um sie kümmern müssen.

1. Fall

In der folgenden Grafik sind als Beispiele die Funktionen

• $f_1(x) = \ln(x)= \log_e(x)$ mit $\mathbb{D} = \mathbb{R}^+$
  
  
• $f_2(x) = \text{ld}(x) = \log_2(x)$ mit $\mathbb{D} = \mathbb{R}^+$
  
  
• $f_3(x) = \lg(x) = \log_{10}(x)$ mit $\mathbb{D} = \mathbb{R}^+$

dargestellt. Die typischen Basen $e$ (natürlicher Logarithmus), $2$ (Zweierlogarithmus) und $10$ (Zehnerlogarithmus) haben wir damit abgedeckt.

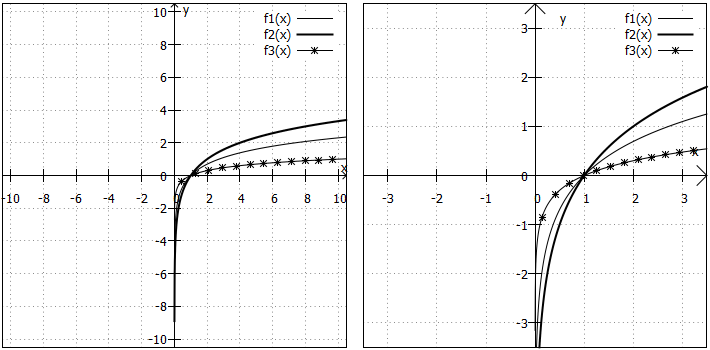
Wertebereich: Der Wertebereich bei klassischen Logarithmusfunktionen ist $\mathbb{D}=\mathbb{R}$.
Da Logarithmusfunktionen eng mit Exponentialfunktionen zusammenhängen (um genau zu sein: sie sind Umkehrfunktionen), "vertauschen" die beiden Funktionstypen Definitions- und Wertebereich: Bei den Exponentialfunktionen ist $\mathbb{D}=\mathbb{R}$ und $\mathbb{W}=\mathbb{R}^+$ und bei Logarithmusfunktionen $\mathbb{D}=\mathbb{R}^+$ und $\mathbb{W}=\mathbb{R}$.

Randverhalten: An den Rändern des Definitionsbereichs passiert Folgendes: x-Werte nahe der $0$ haben sehr kleine Funktionswerte. Sehr große x-Werte haben auch sehr große Funktionswerte. Logarithmusfunktionen wachsen aber trotzdem langsamer als jedes Polynom.

Symmetrie: Die hier betrachteten Logarithmusfunktionen können - aufgrund des einseitig eingeschränkten Definitionsbereichs - nicht symmetrisch sein.

"Besondere Punkte": Einfache Logarithmusfunktionen haben eine Nullstelle bei $x=1$, keine Extrempunkte, Wende- und Polstellen.

Weitere Besonderheiten: Alle diese Logarithmusfunktionen verlaufen durch den Punkt $(1 \mid 0)$, haben also eine gemeinsame Nullstelle.

2. Fall

Nun wird es (noch) interessanter, was die Funktionsverläufe angeht:

• $f_4(x) = \lg\left(x^2+x+6\right)$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_5(x) = \ln\left(\sqrt[6]{(-x+13)^5}\right)-7$ mit $\mathbb{D}=]-\infty; 13[$
  
  
• $f_6(x)=3\cdot\text{ld}\left(\dfrac{x+5}{12}\right)+25$
  
  
• $f_7(x) = -4\ln\left(x^2-4x+4\right)+10$ mit $\mathbb{D}=\mathbb{R}\setminus_{\{2\}}$

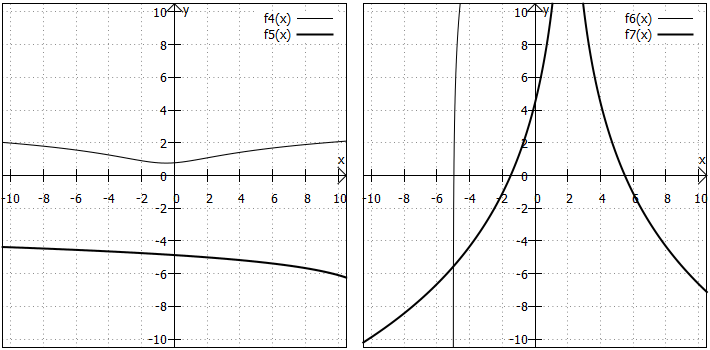
Wie bei den Funktionstypen, die wir in den Kapiteln zuvor betrachtet haben, kann man bei Logarithmusfunktionen, die über den einfachen Fall hinausgehen, keine allgemeinen Aussagen über den Verlauf und besondere Punkte der Graphen treffen. Schauen wir uns einen kleinen Ausschnitt von dem, was so möglich ist, an:

Wertebereich: Der Wertebereich kann (zumindest einseitig) beschränkt sein, wie bei $f_4(x)$ mit $\mathbb{W}=\left[\lg\left(\dfrac{23}{4}\right); \infty\right[$. Bei den anderen hier abgebildeten Funktionen umfasst der Wertebereich alle reellen Zahlen, auch wenn dies bei $f_5(x)$ vielleicht auf den ersten Blick nicht so aussieht ...

Symmetrie: Im Gegensatz zum einfachen Fall sind bei diesen Beispielen zwei achsensymmetrische Graphen dabei: $f_4(x)$ ist achsensymmetrisch zu einer senkrechten Gerade durch $x=-\dfrac{1}{2}$ und $f_7(x)$ ist achsensymmetrisch zu einer senkrechten Gerade durch $x=2$. In beiden Fällen liegt dies an dem quadratischen Term im Argument.

"Besondere Punkte":
In der Grafik wird deutlich, dass nicht jede dieser komplexeren Funktionen eine Nullstelle hat (siehe z. B. $f_4(x)$). $f_5(x)$ hat eine Nullstelle, die allerdings außerhalb des abgebildeten Bereichs liegt, nämlich bei $x_N=13-e^{\frac{42}{5}} \approx -4.434{,}07$, was nochmal deutlich macht, dass die Funktionswerte von $f_5(x)$ im negativen Bereich immer größer werden, auch wenn der Graph hier nahezu konstant aussieht. Aufgrund des quadratischen Terms im Argument hat $f_7(x)$ sogar zwei Nullstellen.
Da die Funktionsterme komplexer sind als im 1. Fall, können hier weitere "besondere Punkte" auftreten, die oben ausgeschlossen waren:

Beispielsweise hat $f_4(x)$ einen Extrempunkt $T \left(-\dfrac{1}{2} \mid \lg\left(\dfrac{23}{4}\right)\right)$. Wie man sehen kann, ist es ein Tiefpunkt.

Zudem hat die Funktion $f_4(x)$ zwei Wendepunkte bei $x_{W1}=\dfrac{1}{2}\left(-1-\sqrt{23}\right) \approx -2{,}90$ und $x_{W2}=\dfrac{1}{2}\left(-1+\sqrt{23}\right) \approx 1{,}90$. Dort ändert sich jeweils das Krümmungsverhalten.

$f_7(x)$ hat eine Polstelle bei $x=2$, weil dort ihr Argument $0$ wird und Logarithmen in diesem Fall nicht definiert sind.

Abschließend fällt auf, dass alle hier betrachteten Beispielgraphen einen Schnittpunkt mit der y-Achse haben, was bei den einfachen Logarithmusfunktionen aus dem 1. Fall nicht auftritt. $f_6(x)$ schneidet die y-Achse bei $3\cdot\text{ld}\left(\dfrac{5}{12}\right)+25\approx 21{,}21$, also außerhalb des im Koordinatensystem abgebildeten Bereichs.

Und noch eine Besonderheit: $f_6(x)$ sieht in dem hier betrachteten Bereich nahezu senkrecht aus, was ja der Funktionsdefinition widersprechen würde. Natürlich ist der Graph von $f_6(x)$ nicht senkrecht, sondern ganz leicht "schief". Das würde man sehen, wenn man in das Koordinatensystem "hineinzoomen" würde.