Dieses Kapitel enthält die folgenden Themen:

• Betragsungleichungen
• Betragsfunktionen

18.2 Betragsgleichungen und -funktionen - Erklärungen

Betragsungleichungen

Zum Lösungen von Ungleichungen, die Terme mit Beträgen enthalten, braucht man eigentlich immer Fallunterscheidungen, die wir uns im Kapitel Ungleichungen schon mal angeschaut hatten, denn der Betrag ist ja unterschiedlich definiert, je nachdem, ob der Term im Betrag positiv bzw. $0$ oder negativ ist. Bei Zahlen lässt sich das ja ohne Weiteres entscheiden, sodass der Betrag dann leicht berechnen werden kann. Durch die Variablen ist das hier nicht ganz so einfach.

Beispielaufgabe:
Schauen wir uns $\left| 2x-1\right|\geq 1+3x$ an.

Lösung:
Will man diese Ungleichung lösen, muss man den Betrag auflösen. Dabei hilft die Definition des Betrages:
$\left|a\right|=a$, wenn $a\geq 0$ und
$\left|a\right|=-a$, wenn $a < 0$

Da wir nicht wissen können, ob $2x-1$ negativ oder nichtnegativ ist, schauen wir uns einfach beide Fälle separat an. Das nennt man eine Fallunterscheidung.

1. Fall: Wir nehmen an $2x-1\geq 0$ oder alternativ $x\geq\frac{1}{2}$ (was das gleiche ist, nur ein bisschen umgeformt). Jetzt greift nämlich die erste Zeile der Betragsdefinition: Da der Term im Betrag in diesem Fall positiv ist, dürfen die Betragsstriche weggelassen werden. Dadurch vereinfacht sich die Ungleichung zu

$\begin{array}{rclcl} 2x-1 & \geq & 1+3x & \vert & -3x+1 \cr -x & \geq & 2 & \vert & \cdot (-1) \cr x & \leq & -2 \end{array}$

Das sieht nach einem schönen Ergebnis aus - ist es aber leider nicht. Wir hatten ja oben bei der Fallunterscheidung angenommen, dass $x\geq\frac{1}{2}$. Das bedeutet, dass nur solche Zahlen überhaupt als Lösungen infrage kommen. Die Frage, die nun noch beantwortet werden muss, ist also: Gibt es Zahlen für die beide Bedingungen gelten? Oder konkret für dieses Beispiel: Gibt es Zahlen, die kleiner oder gleich $-2$ und größer oder gleich $\frac{1} {2}$ sind? Eindeutige Antwort: Solche Zahlen kann es nicht geben! Sie müssten ja gleichzeitig positiv und negativ sein. Also gibt es im 1. Fall keine Lösungen: $\mathbb{L}_1=\emptyset$

2. Fall: Wir nehmen an $2x-1< 0$ oder alternativ $x < \frac{1}{2}$ (auch hier nur ein bisschen umgeformt). Hier müssen wir die zweite Zeile der Betragsdefinition anwenden: Wir schreiben ein Minuszeichen vor den Term und dürfen dafür die Betragsstriche weglassen. Wichtig ist, an die Klammern zu denken, weil sich das Minuszeichen ja auf den gesamten Term auswirken soll. Dadurch vereinfacht sich die Ungleichung zu

$\begin{array}{rclcl} -(2x-1) & \geq & 1+3x \cr -2x+1 & \geq & 1+3x & \vert & -3x-1 \cr -5x & \geq & 0 & \vert & :\left(-5\right) \cr x & \leq & 0 \end{array}$

Auch nun müssen wir natürlich das Rechenergebnis mit der Bedingung, die sich aus der Fallunterscheidung ergeben hat, abgleichen, um eine Aussage über Lösungen treffen zu können. Beide Bedingungen müssen erfüllt sein. Frage: Gibt es Zahlen, die sowohl kleiner als $\frac{1} {2}$ als auch kleiner oder gleich $0$ sind? Hier haben wir Glück, denn alle Zahlen, die kleiner oder gleich $0$ sind, sind natürlich auch kleiner als $\frac{1} {2}$. Die Lösungsmenge lautet hier: $\mathbb{L}_2=\;\rbrack-\infty;0\rbrack$.

Letzter Schritt: Um zur Lösungsmenge der ursprünglichen Ungleichung zu kommen, müssen die beiden Teillösungsmengen zusammengefügt werden. Das tut man mathematisch, indem man die Vereinigungsmenge der beiden Mengen bildet:
$\mathbb{L}=\mathbb{L}_1\cup\mathbb{L}_2=\emptyset\;\cup\;\rbrack-\infty;0\rbrack=\;\rbrack-\infty;0\rbrack$

Bemerkung 1: Das Bilden der Vereinigungsmenge ist bei dieser Aufgabe ein bisschen witzlos, weil $\mathbb{L}_1$ ja leer ist. Es können zu $\mathbb{L}_2$ also gar keine Elemente hinzukommen. Trotzdem gehört dieser Schritt zum vollständigen Lösungsweg dazu. Meist hat man es ja auch mit Teillösungsmengen zu tun, bei denen sich das vereinigen lohnt ...
Bemerkung 2: Hier sieht man wieder, dass eine saubere Fallunterscheidung dazu führt, dass die Aufgabe danach einfacher ist als vorher. Nach der Fallunterscheidung haben wir keinen Betrag mehr in der Ungleichung. Es bleiben zwei kleine lineare Ungleichungen übrig, die in wenigen Schritten gelöst werden können. 

Betragsfunktionen

Definition: Eine Betragsfunktion ist eine Funktion, bei der auf einen Term, der die Variable enthält, ein Betrag angewendet wird.

In der folgenden Grafik sind die Funktionen

• $f_1(x) = \left| x \right|$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_2(x) = -\left| 2(x+3)^2-0{,}1(x+3)-6 \right|$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_3(x) = 0{,}25 \left| (x+4)^3 \right|-3$ mit $\mathbb{D}=\mathbb{R}$
  
  
• $f_4(x) = \left| 12^{x-5}\right|$ mit $\mathbb{D}=\mathbb{R}$

dargestellt. Da grundsätzlich jede Funktion, die wir in den vorherigen Kapiteln kennengelernt haben, Bestandteil einer Betragsfunktion sein kann, gibt es hier keine wirklich typischen Beispiele. Aus diesem Grund ist es hier - im Gegensatz zu den bisher besprochenen Funktionstypen - nicht möglich, allgemeine Aussagen über die Eigenschaften und "besondere Punkte" vom Betragsfunktionen zu treffen. Sie sind einfach zu vielfältig ...

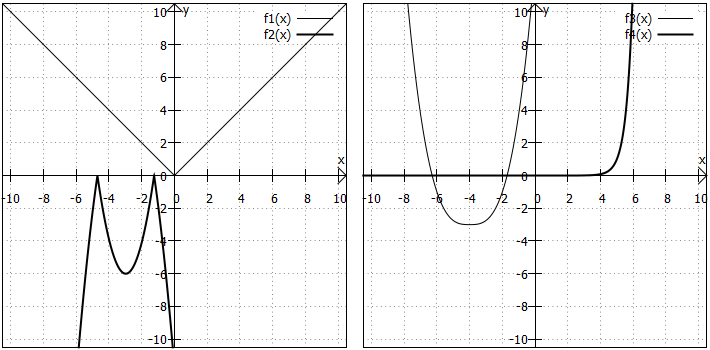
Weitere Besonderheiten: Typisch für eine Betragsfunktion ist ein "Knick" im Funktionsgraphen, der sich ergibt, wenn die Ursprungsfunktion (also die Funktion ohne den Betrag) positive und negative Funktionswerte hatte. Auf diesen "Knick" muss z. B. bei der Differenzialrechnung besonders geachtet werden. Aber wie Sie in der rechten Grafik sehen muss auch nicht jede Betragsfunktion einen "Knick" haben. Das liegt daran, dass $f^*_3(x)=0{,}25 (x+4)^3 -3$ (also die Funktion ohne den Betrag) im Punkt $(-4\mid -3)$ einen Sattelpunkt hat.