SOS Mathematik
Übersicht:
12.1 Eigenschaften und "besondere Punkte" von Funktionen - Aufgaben
Die Aufgaben in diesem Kapitel beschränken sich (größtenteils) auf lineare und quadratische Funktionen, auch wenn man natürlich all diese Konzepte auch für andere Funktionstypen untersuchen kann. Die anderen Funktionstypen müssen Sie ja aber erst kennenlernen, worum wir uns in den folgenden Kapitel kümmern werden.
1. Aufgabe
Prüfen Sie die folgenden Funktionen auf Achsensymmetrie zur y-Achse und Punktsymmetrie zum Koordinatenursprung!
| 1) |
11) |
|
| 2) |
12) |
|
| 3) |
13) |
|
| 4) |
14) |
|
| 5) |
15) |
|
| 6) |
16) |
|
| 7) |
17) |
|
| 8) |
18) |
|
| 9) |
19) |
|
| 10) |
20) |
2. Aufgabe
Finden Sie - wenn vorhanden - die Nullstellen der folgenden Funktionen unter Berücksichtigung des Definitionsbereichs!
1)
mit
2)
mit
3)
mit
4)
mit
5)
mit
3. Aufgabe
Finden Sie - wenn vorhanden - die Extrempunkte der folgenden Funktionen unter Berücksichtigung des Definitionsbereichs! Geben Sie zudem an, ob es sich um Hochpunkte oder Tiefpunkte handelt!
Diese Aufgabe ist so gedacht, dass Sie sie mithilfe von Überlegungen und Argumenten lösen - nicht mithilfe der Differenzialrechnung, die wir ja noch nicht besprochen haben.
| 1) mit |
6) mit |
|
| 2) mit |
7) mit |
|
| 3) mit |
8) mit |
|
| 4) mit |
9) mit |
|
| 5) mit |
10) mit |
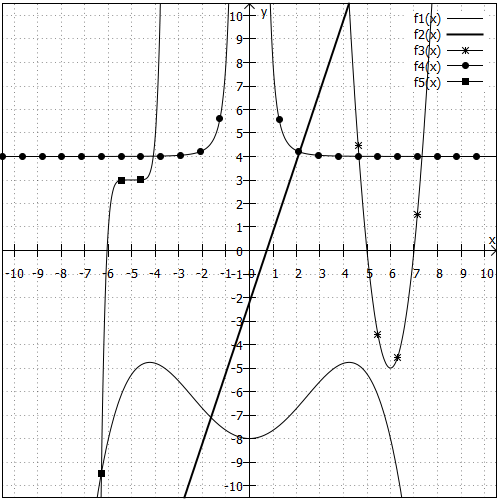
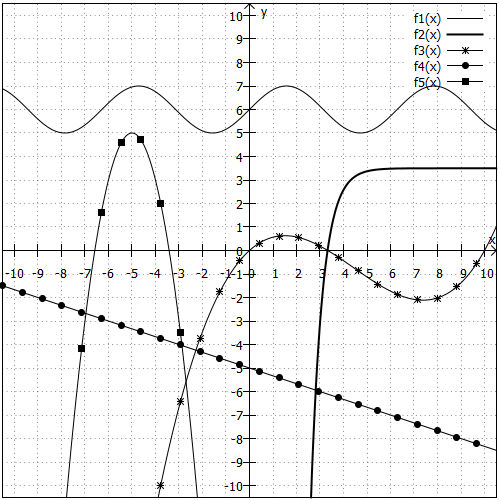
4. Aufgabe
Betrachten Sie die folgenden Graphen und stellen Sie fest, ob und wenn ja, wo die Funktionen einen Wende- oder Sattelpunkt haben!