SOS Mathematik
Dieses Kapitel enthält die folgenden Themen:
- Skizzieren eines Funktionsgraphen
- Eigenschaften - Randverhalten
- Eigenschaften - Symmetrie
- Punkte - Schnittpunkte mit den Achsen/Extrempunkte
- Punkte - Wende-/Sattelpunkte
- Punkte - Polstellen
12.2 Eigenschaften und "besondere Punkte" von Funktionen - Erklärungen
Das Wissen über die Eigenschaften und "speziellen Punkte" von Funktionen/Graphen, um das es in diesem Kapitel geht, ist sehr nützlich und hilft häufig viel mehr als eine ausführliche Wertetabelle. Dazu zwei Beispiele:
- Bei einer Funktion, die achsensymmetrisch zur y-Achse ist, reicht es aus, die Funktionswerte für positive x-Werte (und
) zu berechnen - die entsprechenden Funktionswerte für negative x-Werte erhält man automatisch. Das erspart eine Menge Arbeit ...
- Eine Nullstelle bei
wird man vermutlich gut mithilfe einer Wertetabelle finden. Für eine Nullstelle, die bei
liegt, wird das schon schwieriger ... Vermutlich wird man sie häufig einfach übersehen.
Um solche Erkenntnisse nutzen zu können bzw. Fehler zu vermeiden, ist es enorm wichtig, ein Bild der Funktionsgraphen im Kopf zu haben und ungefähr zu wissen, wie sich ein bestimmter Funktionstyp "verhält". Schauen Sie sich dieses und die nächsten Kapitel daher genau an, um eine Vorstellung von typischen Eigenschaften der verschiedenen Funktionen zu entwickeln. Es soll dabei deutlich werden, wie Funktionsgleichung und Graph zusammenhängen. Vertieft wird dieser Eindruck dann in Ihrem Studium, auch anhand fachbezogener Aufgaben, die auf diesen grundlegenden Aufgaben aufbauen.
Zur Veranschaulichung, warum Funktionsbetrachtungen wichtig sind, hier ein nur leicht abgewandeltes Beispiel einer Klausuraufgabe: "Skizzieren Sie die Funktionen und
und berechnen Sie den Flächeninhalt der eingeschlossenen Fläche!" Wenn Ihre Skizze keine eingeschlossene Fläche enthält, weil Sie einen der Graphen falsch gezeichnet haben, wird die restliche Aufgabe ganz schön schwierig - selbst wenn Sie wissen, wie man die Funktionen integriert!
Skizzieren eines Funktionsgraphen
Bevor es richtig losgeht, noch ein paar Worte zum Skizzieren eines Funktionsgraphen:
Sehr wichtig ist der Unterschied zwischen "Skizze" und "Zeichnung": Wenn in einer Aufgabe nach einer Skizze gefragt ist (oder sich ergibt, dass das sinnvoll ist), müssen Sie keine exakte Zeichnung anfertigen, sondern eben eine Skizze, aus der zwar die wesentlichen Eigenschaften des Graphen hervorgehen, die aber ansonsten ein bisschen ungenau sein darf. Für eine ordentliche Zeichnung muss vorab eigentlich eine detaillierte Kurvendiskussion durchgeführt werden. Um die beiden Funktionen von oben "nur" zu skizzieren, überlegen wir uns:
Zu :
- Es handelt sich um eine quadratische Funktion, also ist ihr Funktionsgraph eine Parabel.
- Die Parabel ist nach unten geöffnet, weil der quadratische Term einen negativen Koeffizienten hat.
- Es handelt sich um eine Normalparabel, da der Koeffizient vor dem quadratischen Term
ist.
- Ihren höchsten Punkt hat die Parabel bei
. Da
subtrahiert wird, wird das Ergebnis ja kleiner ...
- Nullstellen hat
keine. Wie sollte das auch gehen, wenn der größte Wert bei
liegt und die Parabel nach unten geöffnet ist?
- Hier haben wir eine lineare Funktion, also ist ihr Funktionsgraph eine Gerade.
- Die Gerade fällt, da der Koeffizient vor dem
negativ ist.
- Der Graph schneidet die y-Achse bei
, also knapp unterhalb des Schnittpunktes der y-Achse mit dem Graphen von
.
- Wer möchte, kann noch den Schnittpunkt mit der x-Achse ausrechnen. Das ist ja bei linearen Funktionen schnell und unkompliziert möglich.
Eine Skizze könnte also folgendermaßen aussehen:
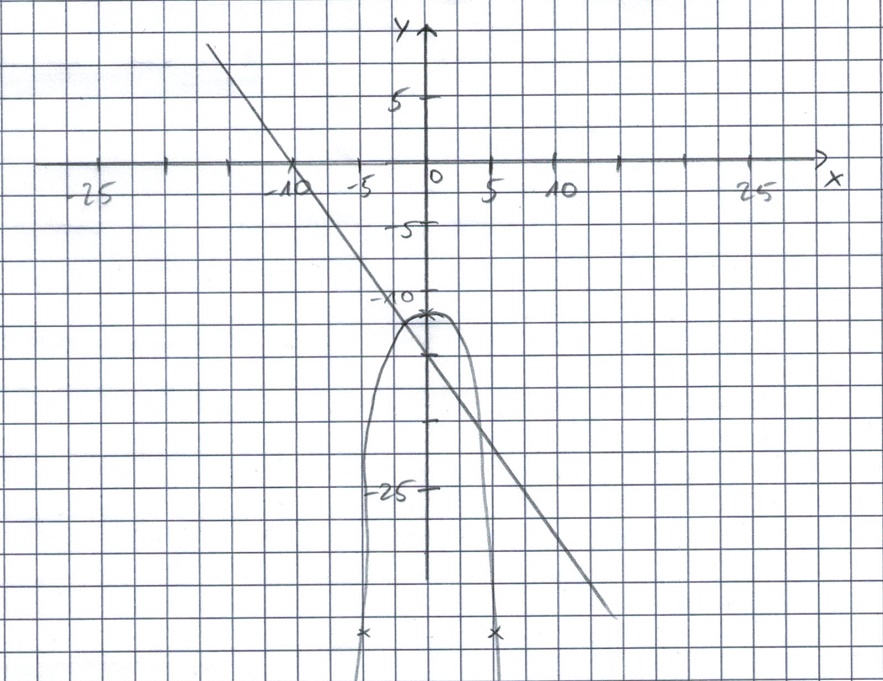
Fertig! Wenn man so an die Fragestellung herangeht, sind Wertetabellen nicht nötig. Vorteil dieser Herangehensweise ist, dass man das "große Ganze" in den Blick nimmt, nämlich den Verlauf des Graphen, und nicht nur einzelne Punkte. Das ist für das Verständnis der Aufgabe meist viel besser. Das "große Ganze" in den Blick zu nehmen ist natürlich auch bei echten Zeichnungen sinnvoll.
Zusätzlich zu der Unterscheidung zwischen Skizze und Zeichnung, sollte man (wie immer) den Aufgabentext gründlich lesen: Wenn in der Aufgabe beispielsweise nur vom ersten Quadranten die Rede ist, reicht natürlich auch eine Skizze von genau diesem Bereich. Man muss sich ja nicht mehr Mühe machen, als nötig ...
Auch die Frage "Zu welchem Zweck erstelle ich die Skizze?" ist hilfreich. Soll die Skizze beispielsweise den Gesamtverlauf der Funktion zeigen oder eher den Bereich rund um den Scheitelpunkt fokussieren?
Zusammengefasst: Erst nachdenken, dann skizzieren oder zeichnen! ;-)
Eigenschaften von Funktionen
Randverhalten
Definition: Das Randverhalten beschreibt den Verlauf der Funktion an den Rändern des Definitionsbereichs.
Da beim Randverhalten (wie der Name schon sagt) nur das Verhalten an den Rändern des Definitionsbereichs interessiert, wird hier nichts über den Verlauf "dazwischen" ausgesagt.
Schauen wir uns als Beispiel die Funktion an. Ihr Definitionsbereich ist
, denn für
würde der Nenner
werden, was ja nicht sein darf. Wenn man den Graphen von
betrachtet, sieht man:
- 1. Pfeil: Läuft
gegen
(anders gesagt: werden die x-Werte immer kleiner), geht
gegen
.
- 2. Pfeil: Läuft
von links in Richtung
, geht
gegen
.
- 3. Pfeil: Läuft
von rechts in Richtung
, geht
gegen
.
- 4. Pfeil: Läuft
gegen
, geht
gegen
.
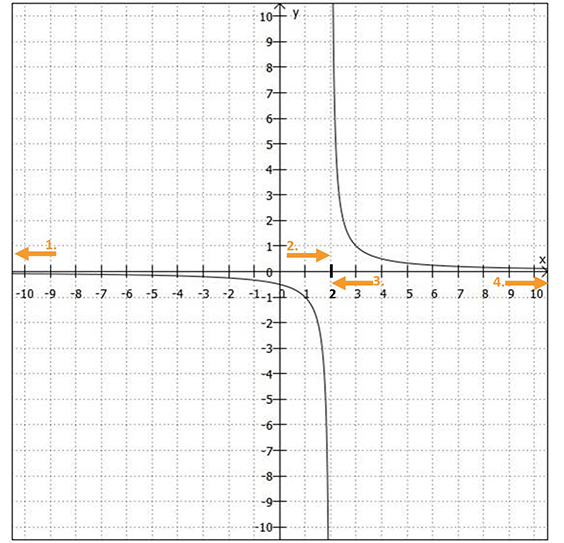
Bemerkung 1: Wie Sie sehen, kann ein Definitionsbereich mehr als zwei Ränder haben.
Bemerkung 2: Um das Randverhalten "mathematisch ordentlich" zu beschreiben, müsste man Grenzwerte betrachten und berechnen, was in diesem Lernmodul nicht gemacht wird.
Die Betrachtung des Randverhaltens ist nützlich, um sich ein Bild vom groben Verlauf des Funktionsgraphen zu machen, und kann dabei helfen, die berechneten "besonderen" Punkte zu plausibilisieren. Wenn Sie beispielsweise an eine Parabel denken, deren Randverhalten "von nach
" ist, muss der Extrempunkt (siehe unten) ein Tiefpunkt sein.
Symmetrie
Viele Objekte (mathematische wie nicht mathematische) haben Symmetrie- oder Spiegelachsen. Das ist nichts Ungewöhnliches. Hier geht es nun um die mathematische Beschreibung des Symmetrieverhaltens bei Funktionen.
Definition: Eine Funktion ist achsensymmetrisch zur y-Achse, wenn gilt
.
Definition: Eine Funktion ist punktsymmetrisch zum Koordinatenursprung, wenn gilt
.
In der folgenden Grafik sind die Funktionen und
zu sehen.
ist achsensymmetrisch zur y-Achse und
punktsymmetrisch zum Koordinatenursprung.
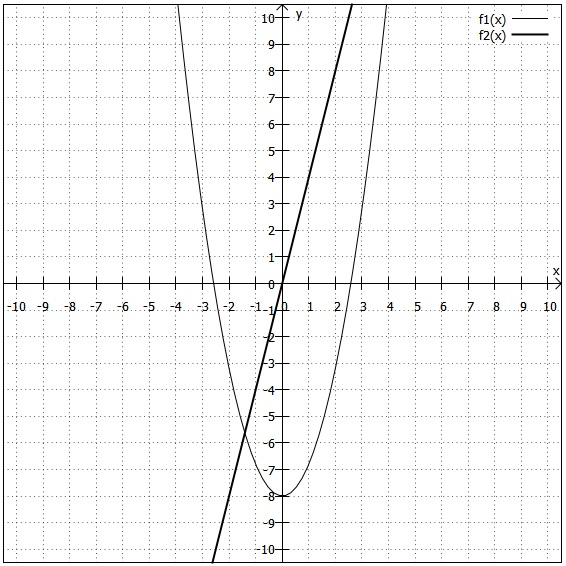
Das kann man natürlich auch mithilfe der in den Definitionen angegebenen Formeln nachweisen:
Achsensymmetrie bei :
Punktsymmetrie bei :
Eine Funktion kann auch zu anderen Geraden außer der y-Achse bzw. zu anderen Punkten außer dem Koordinatenursprung symmetrisch sein. Beispielsweise ist die Funktion punktsymmetrisch zum Punkt
(siehe folgende Grafik).
"Besondere Punkte" einer Funktion
An die "besonderen Punkte", um die es in den kommenden Abschnitten gehen wird, erinnern sich vermutlich die meisten ...
Schnittpunkte mit den Achsen und Extrempunkte
Definition: Eine Funktion hat an einer Stelle
eine Nullstelle, wenn
ist.
Anders formuliert: Eine Funktion hat an einer Stelle
eine Nullstelle, wenn die Funktion an der Stelle
die x-Achse schneidet oder berührt.
Definition: Der y-Achsenabschnitt einer Funktion beschreibt den Schnittpunkt des Funktionsgraphen mit der y-Achse, also den Funktionswert von
bei
.
Definition: Eine Funktion hat an einer Stelle
einen Tiefpunkt, wenn der zu
gehörende Funktionswert
in der unmittelbaren Umgebung von
der kleinste Funktionswert ist.
Definition: Eine Funktion hat an einer Stelle
einen Hochpunkt, wenn der zu
gehörende Funktionswert
in der unmittelbaren Umgebung von
der größte Funktionswert ist.
Definition: Eine Funktion hat an einer Stelle
einen Extrempunkt, wenn die Funktion in
entweder einen Tiefpunkt oder einen Hochpunkt hat.
Wenn man ganz genau sein möchte (und das möchte man in der Mathematik meistens ...), bezeichnet der Begriff "Extremstelle" den x-Wert eines Extrempunktes und der Begriff "Extremum" oder "Extremwert" den zugehörigen y-Wert. Ein Extrempunkt besteht aus dem x-Wert und dem zugehörigen y-Wert.
Selbstverständlich werden hier nur Stellen betrachtet, die im Definitionsbereich liegen!
In der folgenden Grafik sind die Funktionen ,
,
und
zu sehen (Mehr zur Funktion
erfahren Sie im Kapitel Trigonometrie). Die Nullstellen sind mit braunen, die Schnittpunkte mit der y-Achse mit orangen, die Hochpunkte mit dunkelblauen und die Tiefpunkte mit hellblauen Kreisen markiert.
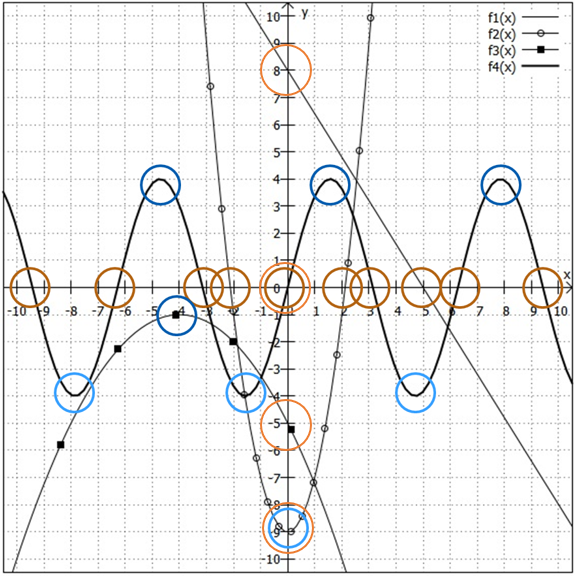
Zur Berechnung von Extremstellen wird in vielen Fällen die Differenzialrechnung benötigt.
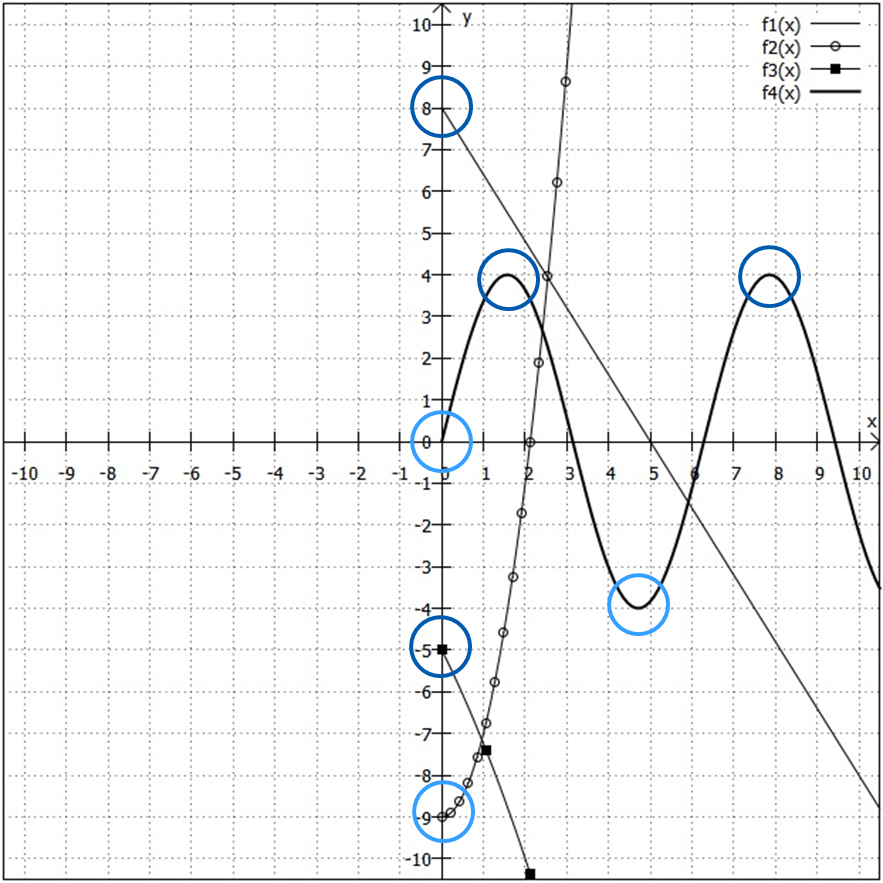
Achtung: Wie in der folgenden Grafik zu sehen ist, hängt es auch vom Definitionsbereich ab, ob eine Funktion an einer Stelle einen Extrempunkt hat. Die Grafik zeigt die gleichen Funktionen wie zuvor, allerdings mit statt
. Alle Extrempunkte im negativen x-Bereich sind weggefallen. Dafür finden sich an der Stelle
, also am unteren Rand des Definitionsbereiches, nun vier Extrempunkte statt wie zuvor nur einer. Solche Extrempunkte heißen - naheliegenderweise - "Randextremwerte".
Um die Nullstellen einer Funktion zu finden, muss der Funktionsterm nullgesetzt und die entstehende Gleichung nach der Variablen aufgelöst werden. Anschließend muss überprüft werden, ob der ermittelte Wert im Definitionsbereich liegt.
Was bedeutet "eine Funktion nullsetzen"?
Setzt man z. B. die Funktion null, erhält man die Gleichung
.
Wende- und Sattelpunkte
Definition: Ein Wendepunkt ist ein Punkt, an dem ein Funktionsgraph sein Krümmungsverhalten ändert - von einer Rechtskrümmung ("Rechtskurve") zu einer Linkskrümmung ("Linkskurve") oder umgekehrt.
Definition: Ein Sattelpunkt ist ein Wendepunkt, an dem die Steigung der Funktion ist, d. h. der Graph der Funktion ist an dieser Stelle horizontal.
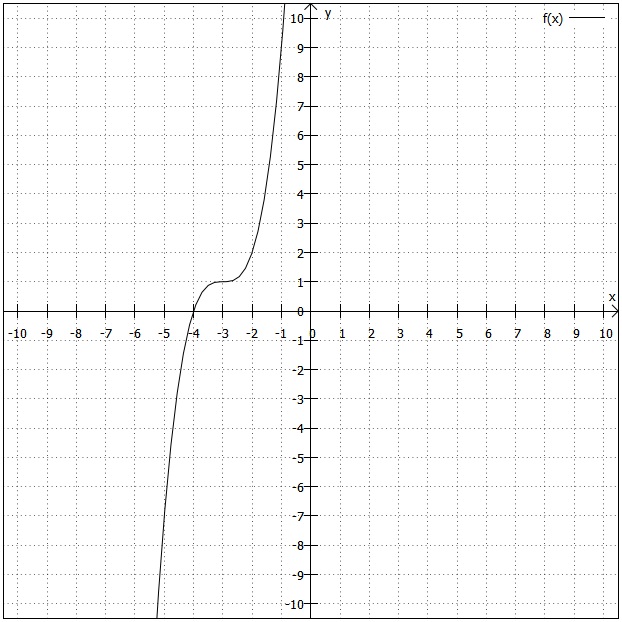
In der folgenden Grafik sind die Funktionen und
zu sehen.
hat einen "normalen" Wendepunkt,
einen Sattelpunkt. Beide sind mit orangefarbenen Kreisen markiert.
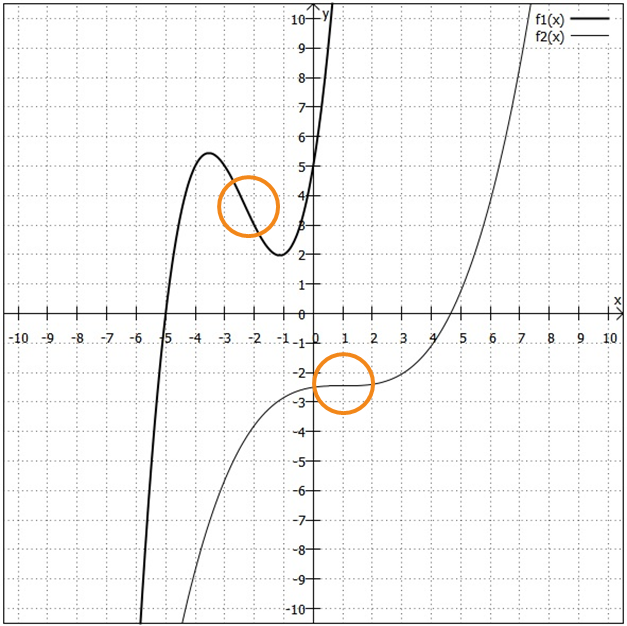
Wende- und Sattelpunkte lassen sich ohne Differenzialrechnung nicht exakt ermitteln.
Polstellen
Definition: Eine Polstelle ist eine Definitionslücke einer Funktion, in deren Umgebung die Funktionswerte beliebig groß oder beliebig klein werden. Etwas salopp formuliert, ist eine Definitionslücke ein "Loch" im Definitionsbereich.
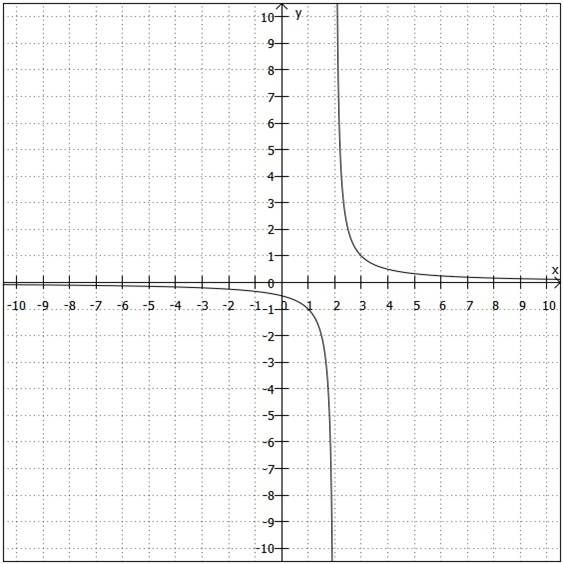
In der folgenden Grafik ist die Funktion zu sehen. Wir hatten oben schon überlegt, dass ihr Definitionsbereich
ist. Direkt links neben der Definitionslücke sind die Funktionswerte beliebig klein, während sie direkt rechts daneben beliebig groß sind.
So, nun haben wir uns angeschaut, was bei Funktionen alles los sein kann, sozusagen die "Basics". In den folgenden Kapiteln werden wir uns verschiedene Funktionstypen detaillierter vornehmen und beleuchten, wie die Eigenschaften und "besondere Punkte" bei ihnen ausgeprägt sind. Im Kapitel 18 dieses Lernmoduls, wenn Sie alle Funktionstypen kennengelernt haben, wird es dann eine übergreifende Aufgabe zu allen Funktionstypen geben.