Übersicht:

• Lösung zur 1. Aufgabe
• Lösung zur 2. Aufgabe
• Lösung zur 3. Aufgabe

11.3 Ungleichungen - Lösungen

1. Aufgabe

Eine Bemerkung vorab: Der Definitionsbereich der Aufgaben 1) bis 11) umfasst jeweils die gesamten reellen Zahlen, weil es sich hier ausschließlich um lineare und quadratische Ungleichungen handelt. Die darin enthaltenen Potenzen kann man uneingeschränkt für jede reelle Zahl bilden. Erst ab Aufgabe 12) gibt es für den Definitionsbereich Einschränkungen.

1)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}2x + 5 & \leq & x-25 & \vert & -5 -x \\x & \leq & -30\end{array}$

Ergebnis: $\mathbb{L} = \left]-\infty;-30\right]$

2)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}6 & \leq & \dfrac{x}{2}+5 & \vert & \cdot 2 \\12 & \leq & x + 10 & \vert & -10 \\2 & \leq & x \\x & \geq & 2\end{array}$

Ergebnis: $\mathbb{L} = \left[2;\infty\right[$

3)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}14(-x+2) & \leq & (4+2x) \cdot 7 \\-14x+28 & \leq & 28+14x & \vert & -28-14x \\-28x & \leq & 0 & \vert & :\left(-28\right) \\x & \geq & 0\end{array}$

Ergebnis: $\mathbb{L} = \left[0;\infty\right[ = \mathbb{R}^+_0$

4)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}8\left(\dfrac{1}{2}-\dfrac{3}{4}x\right) -3 & > & 5-4x \\4-6x-3 & > & 5-4x \\1-6x & > & 5-4x & \vert & +4x-1 \\-2x &>& 4 & \vert & :\left(-2\right) \\x & < &-2\end{array}$

Ergebnis: $\mathbb{L} = \rbrack -\infty;-2\lbrack$

5)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}\dfrac{3-2x}{6} & < & \dfrac{2-x}{2}-1 & \vert & \cdot 6 \\\\3-2x & < & 6\left(\dfrac{2-x}{2}-1\right) \\3-2x & < & 3\left(2-x\right)-6 \\3-2x & < & 6-3x-6 \\3-2x & < & -3x & \vert & +3x-3 \\x & < & -3\end{array}$

Ergebnis: $\mathbb{L} = \rbrack-\infty;-3\lbrack$

Bemerkung: In dieser Ungleichung sind zwar Brüche enthalten, da in den Nennern aber nur natürliche Zahlen stehen, ist das unproblematisch. Es reicht, die ursprüngliche Ungleichung mit $6$ zu multiplizieren, damit beide Nenner "verschwinden".

6)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}(2x-11)\cdot 10 & \geq & -67+4x-8(4-2x) \\20x-110 & \geq & -67+4x-32+16x \\20x-110 & \geq & -99+20x & \vert & -20x \\-110 & \geq & -99\end{array}$

Da $-110$ nun mal nicht größer oder gleich $-99$ ist, hat diese Ungleichung keine Lösung.

Ergebnis: $\mathbb{L} = \emptyset$

7)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}(2x+3)^2-13 & \geq & (x-5)(x+5)+3x(x-3) \\4x^2+12x+9-13 & \geq & x^2-25+3x^2-9x \\4x^2+12x-4 & \geq & 4x^2-9x-25 & \vert & -4x^2 +9x +4 \\21x & \geq & -21 & \vert & :21 \\x & \geq & -1\end{array}$

Ergebnis: $\mathbb{L} = \lbrack -1;\infty \lbrack$

Bemerkung: Diese Ungleichung sieht zwar am Anfang quadratisch aus. Im Laufe der Rechnung heben sich die quadratischen Terme aber gegenseitig auf. Es bleibt eine lineare Ungleichung übrig, die "normal" zu Ende gerechnet werden kann.

8)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}\dfrac{t^2}{2}-3t &>& 56 & \vert & \cdot 2 \\t^2-6t &>& 112 & \vert & -112 \\t^2-6t-112 &>& 0\end{array}$

Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
$\begin{array}{rclcl}t^2-6t-112 & = & 0 &\vert& \text{p-q-Formel}\\t_{1,2} &=& 3\pm\sqrt{9+112} \\\\t_1 &=& 3+11 = 14 \\t_2 &=& 3-11 = -8\end{array}$

Diese Werte liefern uns drei Intervalle:
Von $-\infty$ bis $t_2$: $I_1=\;\rbrack-\infty;-8\lbrack$
Zwischen $t_2$ und $t_1$: $I_2=\;\rbrack-8;14\lbrack$
Von $t_1$ bis $+\infty$ : $I_3=\;\rbrack14;\infty\lbrack$

Prüfen wir nun, für welche Intervalle die Ungleichung erfüllt ist:

Für $I_1$ wählen wir $-10$:
$\begin{array}{rclcl}\dfrac{(-10)^2}{2}-3\cdot(-10) & > & 56 \\50+30 & > & 56 \\80 & > & 56\end{array}$
Es handelt sich um eine wahre Aussage. Also ist $I_1$ Teil der Lösungsmenge.

Für $I_2$ wählen wir $0$:
$\begin{array}{rclcl}\dfrac{0^2}{2}-3\cdot 0 & > & 56 \\0+0 & > & 56 \\0 & > & 56\end{array}$
Es handelt sich um eine falsche Aussage. Also ist $I_2$ nicht Teil der Lösungsmenge.

Für $I_3$ wählen wir $20$:
$\begin{array}{rclcl}\dfrac{20^2}{2}-3\cdot 20 & > & 56 \\200-60 & > & 56 \\140 & > & 56\end{array}$
Es handelt sich um eine wahre Aussage. Also ist $I_3$ Teil der Lösungsmenge.

Ergebnis: Zur Bestimmung der Gesamtlösung müssen wir noch die Intervalle, die als Lösung infrage kommen, vereinigen. In diesem Fall sind das $I_1$ und $I_3$: $\mathbb{L}=I_1 \cup I_3=\;\rbrack-\infty;-8\lbrack \; \cup \;\rbrack14;\infty\lbrack$

9)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}2x^2 &>& -8+7x & \vert & -7x+8 \\2x^2-7x+8 & > & 0 & \vert & :2 \\x^2-\dfrac{7}{2}x+4 & > & 0\end{array}$

Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
$\begin{array}{rclcl}x^2-\dfrac{7}{2}x+4 &=& 0 &\vert& \text{p-q-Formel}\\x_{1,2} & = & \dfrac{7}{4} \pm\sqrt{\dfrac{49}{16}-4} \\& = & \dfrac{7}{4} \pm\sqrt{-\dfrac{15}{16}}\end{array}$

Wir stellen also fest, dass die quadratische Gleichung im Bereich der reellen Zahlen keine Lösungen hat. $x^2-\frac{7}{2}x+4$ ist also immer ungleich $0$ . Auf die ursprüngliche Ungleichung bezogen bedeutet das, dass es keine Werte für $x$ gibt, an denen der Term $2x^2$ genau so groß wie der Term $-8+7x$ ist. Das wiederum bedeutet: Im gesamten Definitionsbereich ist $2x^2$ entweder immer größer oder immer kleiner als $-8+7x$. Die Möglichkeit, dass $2x^2$ nur an einigen Stellen größer und an anderen Stellen kleiner ist, besteht nicht, weil dafür zwischenzeitlich Gleichheit zwischen beiden Termen herrschen müsste, was wir gerade ausgeschlossen haben.

Deswegen ergibt sich für die weitere Prüfung auch nur ein Intervall, das dem Definitionsbereich $\mathbb{D} = \mathbb{R}$ entspricht: $I=\;\rbrack-\infty;+\infty\lbrack$

Prüfen wir nun, ob für das Intervall $I$ die Ungleichung erfüllt ist. Hierzu wählen wir den Wert $0$:
$\begin{array}{rclcl}2 \cdot 0^2 & > & -8 + 7 \cdot 0 \\0 & > & -8\end{array}$
Es handelt sich um eine wahre Aussage. Also ist $I$ Teil der Lösungsmenge. Da wir nur ein Intervall zu betrachten hatten und demzufolge keine weiteren Intervalle zur Lösungsmenge hinzukommen können, ist $I$ gleich der Lösungsmenge. Da $I$ gleich dem Definitionsbereich ist, entspricht auch die Lösungsmenge dem Definitionsbereich. Die Ungleichung ist also für alle Werte $x\in\mathbb{D}$ korrekt.

Ergebnis: $\mathbb{L}=\mathbb{R}$

Bemerkung: Man kann sich das Ganze auch grafisch veranschaulichen. Wenn Sie den Graphen der Funktion $f(x)=x^2-\frac{7}{2}x+4$ zeichnen, sehen Sie, dass die Parabel so weit nach oben verschoben ist, dass sie keine Nullstellen hat. Das entspricht der Tatsache, dass $x^2-\frac{7}{2}x+4$ immer größer als $0$ ist. Wenn Sie sich die Graphen von $f_L(x) =2x^2$ und $f_R(x)=-8+7x$ ansehen, werden Sie analog dazu feststellen, dass $f_L(x)$ immer oberhalb von $f_R(x)$ liegt, sodass es keine gemeinsamen Punkte gibt.

10)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rclcl}16x^2-64 & < & -48x-120 &\vert& +120 \cr 16x^2+56 & < & -48x &\vert& +48x \cr 16x^2+48x+56 & < & 0 &\vert& :16 \cr x^2+3x+\dfrac{7}{2} & < & 0\end{array}$

Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
$\begin{array}{rclcl} x^2+3x+\dfrac{7}{2} &=& 0 &\vert& \text{p-q-Formel} \cr\cr x_{1,2} &=& -\dfrac{3}{2}\pm \sqrt{\dfrac{9}{4}-\dfrac{7}{2}} \cr\cr x_{1,2} &=& -\dfrac{3}{2} \pm \sqrt{-\dfrac{5}{4}} \cr\cr \end{array}$

Da die quadratische Gleichung keine reelle Lösung hat, lässt sich für die weitere Prüfung nur ein Intervall $I$ ableiten, das dem Definitionsbereich $\mathbb{D} = \mathbb{R}$ entspricht: $I=\;\rbrack-\infty;+\infty\lbrack$

Prüfen wir nun, ob für das Intervall $I$ die Ungleichung erfüllt ist. Hierzu wählen wir den Wert $0$:
$\begin{array}{rcl}16\cdot0^2 - 64 & < & -48\cdot 0 - 120 \cr-64 & < & -120\end{array}$
Es handelt sich um eine falsche Aussage. Also ist $I$ nicht Teil der Lösungsmenge. Da keine weiteren Intervalle existieren, die Teil der Lösungsmenge sein könnten, gibt es offensichtlich keinen einzigen Wert für $x$, für den die Ungleichung lösbar ist. Somit entspricht die Lösungsmenge der leeren Menge.

Ergebnis: $\mathbb{L}= \emptyset$

11)
Definitionsbereich: $\mathbb{D} = \mathbb{R}$

Lösung der Ungleichung:
$\begin{array}{rcl}x^2+6x+8 &\geq & 0 \end{array}$

Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
$\begin{array}{rclcl} x^2+6x+8 &=& 0 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& -3\pm\sqrt{9-8} \cr\cr x_1 &=& -3+1 = -2 \cr x_2 &=& -3-1 = -4 \end{array}$

Diese Werte liefern uns drei Intervalle:
Von $-\infty$ bis $x_2$: $I_1=\;\rbrack-\infty;-4\lbrack$
Zwischen $x_2$ und $x_1$: $I_2=\;\rbrack-4;-2\lbrack$
Von $x_1$ bis $+\infty$ : $I_3=\;\rbrack-2;\infty\lbrack$

Prüfen wir nun, für welche Intervalle die Ungleichung erfüllt ist:

Für $I_1$ wählen wir $-5$:
$\begin{array}{rclcl}(-5)^2+6 \cdot (-5)+8 &\geq& 0 \cr 3 &\geq& 0\end{array}$
Es handelt sich um eine wahre Aussage. Also ist $I_1$ Teil der Lösungsmenge.

Für $I_2$ wählen wir $-3$:
$\begin{array}{rclcl}(-3)^2+6 \cdot (-3)+8 &\geq& 0 \cr -1 &\geq& 0 \cr\cr\end{array}$
Es handelt sich um eine falsche Aussage. Also ist $I_2$ nicht Teil der Lösungsmenge.

Für $I_3$ wählen wir $0$:
$\begin{array}{rclcl}0^2+6 \cdot 0+8 &\geq& 0 \cr 8 &\geq& 0 \cr\cr\end{array}$
Es handelt sich um eine wahre Aussage. Also ist $I_3$ Teil der Lösungsmenge.

Da die Ungleichung ein Größergleichzeichen enthält, sind auch die oben berechneten Nullstellen der quadratischen Gleichung Teil der Lösungsmenge.

Ergebnis: $\mathbb{L}=I_1 \cup \{-4\} \cup \{-2\} \cup I_3 =\;\rbrack-\infty;-4\rbrack \; \cup \;\lbrack-2;\infty\lbrack$

Bemerkung für die folgenden Aufgaben: Bei den folgenden Ungleichungen müssen wir uns den Definitionsbereich $\mathbb{D}$ genauer anschauen, weil nun Variablen im Nenner stehen und bekanntermaßen durch $0$ nicht geteilt werden darf. Wir müssen also prüfen, für welche Werte der Variable der Nenner nicht $0$ wird. Für die Überprüfung setzen wir jeweils den Nennerterm ungleich $0$, lösen die zugehörige Ungleichung und leiten aus dem Ergebnis den Definitionsbereich ab.

12)
Bestimmung des Definitionsbereichs:
$\begin{array}{rcl}x &\neq & 0\end{array}$

Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\{0\}}$.

Lösung der Ungleichung:
$\dfrac{1}{x} \geq 5$

Bei dieser Ungleichung ist eine Fallunterscheidung notwendig, da wir mit $x$ multiplizieren müssen. 

Fall 1: Wir nehmen an, dass $x>0$ ist:
$\begin{array}{rclcl}\dfrac{1}{x} & \geq & 5 & \vert & \cdot x \\1 & \geq & 5x &\vert& :5 \\\dfrac{1}{5} & \geq & x\end{array}$
Der Abgleich der Bedingung $x > 0$ mit dem Ergebnis $x \leq \dfrac{1}{5}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_1 = \left] 0;\dfrac{1}{5}\right]$

Fall 2: Wir nehmen an, dass $x < 0$ ist:
$\begin{array}{rclcl}\dfrac{1}{x} & \geq & 5 &\vert & \cdot x \\1 & \leq & 5x & \vert & : 5 \\\dfrac{1}{5} & \leq & x\end{array}$
Der Abgleich der Bedingung $x < 0$ mit dem Ergebnis $x \geq \dfrac{1}{5}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_2=\emptyset$

Ergebnis: Die Gesamtlösungsmenge ist die Vereinigung der Teillösungsmengen: $\mathbb{L} = \mathbb{L}_1 \cup \mathbb{L}_2 = \left] 0;\dfrac{1}{5} \right] \cup \emptyset = \left] 0;\dfrac{1}{5} \right]$

Bemerkung: Den Fall $x=0$ müssen wir nicht betrachten, weil er schon durch den Definitionsbereich ausgeschlossen ist. Durch $0$ darf man ja nun mal nicht teilen ...

13)
Bestimmung des Definitionsbereichs:
$\begin{array}{rclll} x+3 &\neq& 0 &\vert& -3 \\x &\neq& -3\end{array}$

Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\{-3\}}$.

Lösung der Ungleichung:
$\dfrac{1}{x+3} < -5$

Bei dieser Ungleichung ist eine Fallunterscheidung notwendig, da wir mit $\left(x+3\right)$ multiplizieren müssen.

Fall 1: Wir nehmen an, dass $x+3>0$, also $x>-3$, ist:
$\begin{array}{rclcll}\dfrac{1}{x+3} & < & -5 &\vert & \cdot\left(x+3\right)\\1 & < & -5\left(x+3\right)\\1 & < & -5x-15 &\vert & +15\\16 & < & -5x &\vert & :\left(-5\right)\\-\dfrac{16}{5} &>& x\end{array}$
Der Abgleich der Bedingung $x > -3$ mit dem Ergebnis $x < -\dfrac{16}{5}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_1 = \emptyset$

Fall 2: Wir nehmen an, dass $x+3 < 0$, also $x < -3$, ist:
$\begin{array}{rclcll} \dfrac{1}{x+3} & < & -5 &\vert & \cdot\left(x+3\right)\\1 &>& -5\left(x+3\right)\\1 &>& -5x-15 &\vert & +15\\16 &>& -5x &\vert & :\left(-5\right)\\-\dfrac{16}{5} & < & x \end{array}$
Der Abgleich der Bedingung $x < -3$ mit dem Ergebnis $x > -\dfrac{16}{5}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_2 = \left]-\dfrac{16}{5};-3\right[$

Ergebnis: $\mathbb{L}=\mathbb{L}_1 \cup \mathbb{L}_2 = \emptyset \cup \left]-\dfrac{16}{5};-3\right[ = \left]-\dfrac{16}{5};-3\right[$

14)
Bestimmung des Definitionsbereichs:
$\begin{array}{rclll} -y+13 &\neq& 0 &\vert& +y \\13 &\neq& y\end{array}$

Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\left\{13\right\}}$.

Lösung der Ungleichung:
$\dfrac{20}{-y+13} \leq 15$

Bei dieser Ungleichung ist eine Fallunterscheidung notwendig, da wir mit $\left(-y+13\right)$ multiplizieren müssen.

Fall 1: Wir nehmen an, dass $-y + 13 > 0$, also $y < 13$, ist:
$\begin{array}{rclcll}\dfrac{20}{-y+13} &\leq & 15 &\vert & \cdot\left(-y+13\right)\\20 &\leq & 15\left(-y+13\right)\\20 &\leq & -15y+195 &\vert & -195\\-175 &\leq & -15y &\vert & :\left(-15\right)\\\dfrac{35}{3} &\geq & y\end{array}$
Der Abgleich der Bedingung $y < 13$ mit dem Ergebnis $y\leq \dfrac{35}{3}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_1 = \left]-\infty;\dfrac{35}{3}\right]$

Fall 2: Wir nehmen an, dass $-y + 13 < 0$, also $y > 13$, ist:
$\begin{array}{rclcll}\dfrac{20}{-y+13} &\leq & 15 &\vert & \cdot\left(-y+13\right)\\20 &\geq & 15\left(-y+13\right)\\20 &\geq & -15y+195 &\vert & -195\\-175 &\geq & -15y &\vert & :\left(-15\right)\\\dfrac{35}{3} &\leq & y\end{array}$
Der Abgleich der Bedingung $y > 13$ mit dem Ergebnis $y\geq \dfrac{35}{3}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_2 = \left]13;\infty\right[$

Ergebnis: $\mathbb{L}=\mathbb{L}_1 \cup \mathbb{L}_2=\left]-\infty;\dfrac{35}{3}\right] \cup \left]13;\infty\right[$

15)
Bestimmung des Definitionsbereichs:
$\begin{array}{rclll} 2x+3 &\neq& 0 &\vert& -3 \\2x &\neq& -3 &\vert& :2 \\x &\neq& -\dfrac{3}{2}\end{array}$

Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\left\{-\frac{3}{2}\right\}}$.

Lösung der Ungleichung:
$\dfrac{5x-7}{2x+3} < 4$

Bei dieser Ungleichung ist eine Fallunterscheidung notwendig, da wir mit $\left(2x+3\right)$ multiplizieren müssen.

Fall 1: Wir nehmen an, dass $2x + 3 > 0$, also $x > -\dfrac{3}{2}$, ist:
$\begin{array}{rclcll}\dfrac{5x-7}{2x+3} & < & 4 &\vert & \cdot\left(2x+3\right)\\5x-7 & < & 4\left(2x+3\right)\\5x-7 & < & 8x+12 &\vert & -12-5x\\-19 & < & 3x &\vert & :3\\-\dfrac{19}{3} & < & x\end{array}$
Der Abgleich der Bedingung $x > -\dfrac{3}{2}$ mit dem Ergebnis $x > -\dfrac{19}{3}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_1 = \left]-\dfrac{3}{2};\infty\right[$

Fall 2: Wir nehmen an, dass $2x + 3 < 0$, also $x < -\dfrac{3}{2}$, ist:
$\begin{array}{rclcll}\dfrac{5x-7}{2x+3} & < & 4 &\vert & \cdot\left(2x+3\right)\\5x-7 &> & 4\left(2x+3\right)\\5x-7 &>& 8x+12 &\vert & -12-5x\\-19 &>& 3x &\vert & :3\\-\dfrac{19}{3} &> & x\end{array}$
Der Abgleich der Bedingung $x < -\dfrac{3}{2}$ mit dem Ergebnis $x < -\dfrac{19}{3}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_2 = \left]-\infty;-\dfrac{19}{3}\right[$

Ergebnis: $\mathbb{L}=\mathbb{L}_1 \cup \mathbb{L}_2=\left]-\infty;-\dfrac{19}{3}\right[ \cup \left]-\dfrac{3}{2};\infty\right[$

16)
Bestimmung des Definitionsbereichs:
$\begin{array}{rclll}4+2x &\neq& 0 &\vert& -4 \\2x &\neq& -4 &\vert& :2\\x &\neq& -2\end{array}$

Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\left\{-2\right\}}$.

Lösung der Ungleichung:
$\begin{array}{rclcll}2-\dfrac{6(x+3)}{4+2x} &>& 0 &\vert & +\dfrac{6(x+3)}{4+2x}\\2 &>& \dfrac{6(x+3)}{4+2x} \end{array}$

Bei dieser Ungleichung ist eine Fallunterscheidung notwendig, da wir mit $(4+2x)$ multiplizieren müssen.

Fall 1: Wir nehmen an, dass $4+2x > 0$, also $x > -2$, ist:
$\begin{array}{rclcll}2 & > & \dfrac{6(x+3)}{4+2x} & \vert & \cdot(4+2x)\\2(4+2x) & > & 6(x+3) \\8+4x & > & 6x+18 &\vert & -4x -18\\-10 & > & 2x &\vert & :2\\-5 & > & x\end{array}$
Der Abgleich der Bedingung $x > -2$ mit dem Ergebnis $x < -5$ führt zu folgender Teillösungsmenge: $\mathbb{L}_1 = \emptyset$

Fall 2: Wir nehmen an, dass $4+2x < 0$, also $x < -2$, ist:
$\begin{array}{rclcll}2 & > & \dfrac{6(x+3)}{4+2x} & \vert & \cdot(4+2x)\\2(4+2x) & < & 6(x+3) \\8+4x & < & 6x+18 &\vert & -4x -18\\-10 & < & 2x &\vert & :2\\-5 & < & x\end{array}$
Der Abgleich der Bedingung $x < -2$ mit dem Ergebnis $x > -5$ führt zu folgender Teillösungsmenge: $\mathbb{L}_2 = \left]-5;-2\right[$

Ergebnis: $\mathbb{L}=\mathbb{L}_1 \cup \mathbb{L}_2=\emptyset \cup \left]-5;-2\right[ = \left]-5;-2\right[$

17)
Bestimmung des Definitionsbereichs:
1. linker Nenner:
$\begin{array}{rclll}x+5 &\neq& 0 &\vert& -5 \\x &\neq& -5\end{array}$

2. linker Nenner:
$\begin{array}{rclll}x-5 &\neq& 0 &\vert& +5 \\x &\neq& 5\end{array}$

Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\left\{-5; 5\right\}}$.

Lösung der Ungleichung:
$\dfrac{1}{x+5}-\dfrac{1}{x-5}>-1$

Bei dieser Ungleichung ist eine Fallunterscheidung notwendig, da wir mit $(x+5)$ multiplizieren müssen.

Fall 1: Wir nehmen an, dass $x + 5 > 0$, also $x > -5$, ist:
$\begin{array}{rclcl}\dfrac{1}{x+5}-\dfrac{1}{x-5} & > & -1 &\vert & \cdot\left(x+5\right) \cr\cr 1-\dfrac{x+5}{x-5} & > & -(x+5)\end{array}$

Hier ist eine weitere Fallunterscheidung notwendig, da wir auch noch mit $(x-5)$ multiplizieren müssen.

Fall 1.1: Wir nehmen an, dass $x - 5 > 0$, also $x > 5$, ist:
$\begin{array}{rclcl}1-\dfrac{x+5}{x-5} & > & -(x+5) & \vert & \cdot \left(x-5\right) \\x-5 - (x+5) & > & -(x+5)(x-5) \\x-5-x-5 & > & -\left(x^2 -25\right) \\-10 & > & -x^2 + 25 & \vert & -25 \\-35 & > & -x^2 & \vert & +x^2 +35 \\x^2 & > & 35 &\vert & \sqrt{} \\\vert x\vert &>& \sqrt{35} \approx 5{,}92\end{array}$
Es ergeben sich also zwei mögliche Lösungsintervalle: $x < -\sqrt{35}$ oder $x > \sqrt{35}$.

Der Abgleich der Bedingungen $x > -5$ und $x > 5$ mit dem Ergebnis $x < -\sqrt{35}$ oder $x > \sqrt{35}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_{1.1} = \left]\sqrt{35};\infty\right[$

Fall 1.2: Wir nehmen an, dass $x - 5 < 0$, also $x < 5$, ist:
$\begin{array}{rclcl}1-\dfrac{x+5}{x-5} & > & -(x+5) & \vert & \cdot \left(x-5\right) \\x-5 - (x+5) & < & -(x+5)(x-5) \\x-5-x-5 & < & -\left(x^2 -25\right) \\-10 & < & -x^2 + 25 & \vert & -25 \\-35 & < & -x^2 & \vert & +x^2 +35 \\x^2 & < & 35 &\vert & \sqrt{} \\\vert x\vert & < & \sqrt{35} \approx 5{,}92\end{array}$
Es ergibt sich das mögliche Lösungsintervall: $-\sqrt{35} < x < \sqrt{35}$.

Der Abgleich der Bedingungen $x > -5$ und $x < 5$ mit dem Ergebnis $-\sqrt{35} < x < \sqrt{35}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_{1.2} = \left]-5;5\right[$

Fall 2: Wir nehmen an, dass $x + 5 < 0$, also $x < -5$, ist:
$\begin{array}{rclcl}\dfrac{1}{x+5}-\dfrac{1}{x-5} & > & -1 &\vert & \cdot\left(x+5\right) \cr\cr 1-\dfrac{x+5}{x-5} & < & -(x+5)\end{array}$

Hier ist eine weitere Fallunterscheidung notwendig, da wir auch noch mit $(x-5)$ multiplizieren müssen.

Fall 2.1: Wir nehmen an, dass $x - 5 > 0$, also $x > 5$, ist:
Da sich schon die Bedingungen von Fall 2 und Fall 2.1, nämlich $x < -5$ und $x > 5$, widersprechen, müssen wir diesen Fall nicht weiter bearbeiten: $\mathbb{L}_{2.1} = \emptyset$

Fall 2.2: Wir nehmen an, dass $x - 5 < 0$, also $x < 5$, ist:

$\begin{array}{rclcl}1-\dfrac{x+5}{x-5} & < & -(x+5) & \vert & \cdot \left(x-5\right) \\x-5 - (x+5) & > & -(x+5)(x-5) \\x-5-x-5 & > & -\left(x^2 -25\right) \\-10 & > & -x^2 + 25 & \vert & -25 \\-35 & > & -x^2 & \vert & +x^2 +35 \\x^2 & > & 35 &\vert & \sqrt{} \\\vert x\vert &>& \sqrt{35} \approx 5{,}92\end{array}$
Es ergeben sich also zwei mögliche Lösungsintervalle: $x < -\sqrt{35}$ oder $x > \sqrt{35}$.

Der Abgleich der Bedingungen $x < -5$ und $x < 5$ mit dem Ergebnis $x < -\sqrt{35}$ oder $x > \sqrt{35}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_{2.2} = \left]-\infty;-\sqrt{35}\right[$

Ergebnis:
$\begin{array}{rcl} \mathbb{L} &=& \mathbb{L}_{1.1} \cup \mathbb{L}_{1.2} \cup \mathbb{L}_{2.1} \cup \mathbb{L}_{2.2} \cr &=& \left]-\infty;-\sqrt{35}\right[ \cup \left]-5;5\right[ \cup \emptyset \cup \left]\sqrt{35};\infty\right[ \cr &=& \left]-\infty;-\sqrt{35}\right[ \cup \left]-5;5\right[ \cup \left]\sqrt{35};\infty\right[ \end{array}$

18)
Bestimmung des Definitionsbereichs:
1. linker Nenner:
$\begin{array}{rclll}3+x &\neq& 0 &\vert& -3 \\x &\neq& -3\end{array}$

2. linker Nenner:
$\begin{array}{rclll}3-x &\neq& 0 &\vert& +x \\3 &\neq& x\end{array}$

Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\left\{-3; 3\right\}}$.

Lösung der Ungleichung:
$\dfrac{3x}{3+x}+\dfrac{2x}{3-x}>1$

Bei dieser Ungleichung ist eine Fallunterscheidung notwendig, da wir mit $(3+x)$ multiplizieren müssen.

Fall 1: Wir nehmen an, dass $3 + x > 0$, also $x > -3$, ist:
$\begin{array}{rclcl}\dfrac{3x}{3+x}+\dfrac{2x}{3-x} & > & 1 &\vert & \cdot\left(3+x\right) \cr\cr 3x+\dfrac{2x(3+x)}{3-x} & > & 3+x\end{array}$

Hier ist eine weitere Fallunterscheidung notwendig, da wir auch noch mit $(3-x)$ multiplizieren müssen.

Fall 1.1: Wir nehmen an, dass $3 - x > 0$, also $x < 3$, ist:
$\begin{array}{rclcl}3x+\dfrac{2x(3+x)}{3-x} & > & 3+x & \vert & \cdot \left(3-x\right) \\3x(3-x) + 2x(3+x) & > & (3+x)(3-x) \\9x-3x^2+6x+2x^2 & > & 9 - x^2 \\15x - x^2 & > & 9 - x^2 & \vert & +x^2 \\15x & > & 9 & \vert & :15 \\x & > & \dfrac{3}{5}\end{array}$
Der Abgleich der Bedingungen $x > -3$ und $x < 3$ mit dem Ergebnis $x > \dfrac{3}{5}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_{1.1} = \left]\dfrac{3}{5};3\right[$

Fall 1.2: Wir nehmen an, dass $3 - x < 0$, also $x > 3$, ist:
$\begin{array}{rclcl}3x+\dfrac{2x(3+x)}{3-x} & > & 3+x & \vert & \cdot \left(3-x\right) \\3x(3-x) + 2x(3+x) & < & (3+x)(3-x) \\9x-3x^2+6x+2x^2 & < & 9 - x^2 \\15x - x^2 & < & 9 - x^2 & \vert & +x^2 \\15x & < & 9 & \vert & :15 \\x & < & \dfrac{3}{5}\end{array}$
Der Abgleich der Bedingungen $x > -3$ und $x > 3$ mit dem Ergebnis $x < \dfrac{3}{5}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_{1.2} = \emptyset$

Fall 2: Wir nehmen an, dass $3 + x < 0$, also $x < -3$, ist:
$\begin{array}{rclcl}\dfrac{3x}{3+x}+\dfrac{2x}{3-x} & > & 1 &\vert & \cdot\left(3+x\right) \cr\cr 3x+\dfrac{2x(3+x)}{3-x} & < & 3+x\end{array}$

Hier ist eine weitere Fallunterscheidung notwendig, da wir auch noch mit $(3-x)$ multiplizieren müssen.

Fall 2.1: Wir nehmen an, dass $3 - x > 0$, also $x < 3$, ist:
$\begin{array}{rclcl}3x+\dfrac{2x(3+x)}{3-x} & < & 3+x & \vert & \cdot \left(3-x\right) \\3x(3-x) + 2x(3+x) & < & (3+x)(3-x) \\9x-3x^2+6x+2x^2 & < & 9 - x^2 \\15x - x^2 & < & 9 - x^2 & \vert & +x^2 \\15x & < & 9 & \vert & :15 \\x & < & \dfrac{3}{5}\end{array}$
Der Abgleich der Bedingungen $x < -3$ und $x < 3$ mit dem Ergebnis $x < \dfrac{3}{5}$ führt zu folgender Teillösungsmenge: $\mathbb{L}_{2.1} = \left]-\infty;-3\right[$

Fall 2.2: Wir nehmen an, dass $3 - x < 0$, also $x > 3$, ist:
Da sich schon die Bedingungen von Fall 2 und Fall 2.2, nämlich $x < -3$ und $x > 3$, widersprechen, müssen wir diesen Fall nicht weiter bearbeiten: $\mathbb{L}_{2.2} = \emptyset$

Ergebnis:
$\begin{array}{rcl} \mathbb{L} &=& \mathbb{L}_{1.1} \cup \mathbb{L}_{1.2} \cup \mathbb{L}_{2.1} \cup \mathbb{L}_{2.2} \cr &=& \left]\dfrac{3}{5};3\right[ \cup \emptyset \cup \left]-\infty;-3\right[\ \cup \emptyset \cr &=& \left]-\infty;-3\right[\ \cup \left]\dfrac{3}{5};3\right[ \end{array}$

19)
Bestimmung des Definitionsbereichs:
1. linker Nenner:
$\begin{array}{rclll}x-4 &\neq& 0 &\vert& +4 \\x &\neq& 4 \end{array}$

2. linker Nenner:
$\begin{array}{rclll}x-2 &\neq& 0 &\vert& +2 \\x &\neq& 2\end{array}$

Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\left\{2; 4\right\}}$.

Lösung der Ungleichung:
Diese Ungleichung lösen wir auf einem anderen Weg als die Aufgaben 17) und 18), nämlich indem wir die Brüche zuerst subtrahieren, um dann mit dem Hauptnenner zu multiplizieren. Das erspart uns - wie wir sehen werden - eine doppelte Fallunterscheidung. Allerdings ist die Rechnung, bis wir zur Fallunterscheidung kommen, länger, weil (natürlich!) die ganz normalen Regeln für das Rechnen mit Brüchen, Klammern etc. berücksichtigt werden müssen ... Natürlich kann auch bei dieser Aufgabe mit beiden Nennern einzeln multipliziert werden. Beide Wege führen zur selben Lösung.

$\begin{array}{rclcll}\dfrac{x-7}{x-4} - \dfrac{2x-5}{x-2} & \leq & 0 \\\\\dfrac{(x-7)(x-2)}{(x-4)(x-2)} - \dfrac{(2x-5)(x-4)}{(x-2)(x-4)} & \leq & 0 \\\\\dfrac{x^2-2x-7x+14}{(x-2)(x-4)} - \dfrac{2x^2-8x-5x+20}{(x-2)(x-4)} & \leq & 0 \\\\\dfrac{x^2-9x+14}{(x-2)(x-4)} - \dfrac{2x^2-13x+20}{(x-2)(x-4)} & \leq & 0 \\\\\dfrac{x^2-9x+14-\left(2x^2-13x+20\right)}{(x-2)(x-4)} & \leq & 0 \\\\\dfrac{x^2-9x+14-2x^2+13x-20}{(x-2)(x-4)} & \leq & 0 \\\\\dfrac{-x^2+4x-6}{(x-2)(x-4)} & \leq & 0\end{array}$

Bei dieser Ungleichung ist eine Fallunterscheidung notwendig, da wir mit $(x-2)(x-4)$ multiplizieren müssen.

Fall 1: Wir nehmen an, dass $(x-2)(x-4) > 0$ ist. Das ist genau dann der Fall, wenn beide Faktoren positiv oder beide Faktoren negativ sind. Somit muss $x < 2$ oder $x > 4$ sein:
$\begin{array}{rclcll}\dfrac{-x^2+4x-6}{(x-2)(x-4)} & \leq & 0 & \vert & \cdot (x-2)(x-4) \\-x^2 + 4x - 6 & \leq & 0 & \vert & \cdot (-1) \\x^2 - 4x + 6 & \geq & 0 \\\end{array}$

Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
$\begin{array}{rclcl} x^2 - 4x + 6 &=& 0 &\vert& \text{p-q-Formel} \cr x_{1,2} &=& 2\pm\sqrt{4-6} \cr x_{1,2} &=& 2\pm\sqrt{-2} \cr\cr \end{array}$

Da die quadratische Gleichung keine reelle Lösung hat, lässt sich für die weitere Prüfung nur ein Intervall $I$ ableiten, das dem Definitionsbereich $\mathbb{D} = \mathbb{R}\setminus_{\left\{2; 4\right\}}$ entspricht.

Prüfen wir nun, ob für das Intervall $I$ die Ungleichung erfüllt ist. Hierzu wählen wir den Wert $0$:
$\begin{array}{rclcll}0^2 - 4 \cdot 0 + 6 & \geq & 0 \\6 & \geq & 0\end{array}$
Es handelt sich um eine wahre Aussage. Die Ungleichung ist also für alle Werte $x\in\mathbb{D}$ korrekt. Nun müssen wir dieses Ergebnis noch mit der Bedingung von Fall 1, also $x < 2$ oder $x > 4$, abgleichen. Daraus ergibt sich folgende Teillösungsmenge: $\mathbb{L}_1=\left]-\infty;2\right[\ \cup \left]4;\infty\right[$

Fall 2: Wir nehmen an, dass $(x-2)(x-4) < 0$ ist. Das ist genau dann der Fall, wenn die Faktoren ein unterschiedliches Vorzeichen haben. Das ist für $2 < x < 4$ der Fall:
$\begin{array}{rclcll}\dfrac{-x^2+4x-6}{(x-2)(x-4)} & \leq & 0 & \vert & \cdot (x-2)(x-4) \\-x^2 + 4x - 6 & \geq & 0 & \vert & \cdot (-1) \\x^2 - 4x + 6 & \leq & 0 \\\end{array}$

Wir wissen bereits aus der Betrachtung von Fall 1, dass die zugehörige quadratische Gleichung keine Lösung hat, daher können wir uns das erneute Lösen der quadratischen Gleichung sparen. Außerdem wissen wir auch aus Fall 1, dass $x^2 - 4x + 6$ immer positiv ist. Somit kann die Ungleichung $x^2 - 4x + 6 \leq 0$ niemals erfüllt werden. Das führt zu folgender Teillösungsmenge: $\mathbb{L}_2=\emptyset$

Ergebnis: $\mathbb{L}=\mathbb{L}_{1} \cup \mathbb{L}_{2}=\left]-\infty;2\right[\ \cup \left]4;\infty\right[ \cup \emptyset = \left]-\infty;2\right[\ \cup \left]4;\infty\right[$

20)
Bestimmung des Definitionsbereichs:
$\begin{array}{rclcl}x^2-x-2&=&0 \\x_{1,2}&=&\dfrac{1}{2}\pm\sqrt{\dfrac{1}{4}+2} \\\\x_1 &=& \dfrac{1}{2}+\dfrac{3}{2} = 2 \\x_2 &=& \dfrac{1}{2}-\dfrac{3}{2} = -1\end{array}$

Der Definitionsbereich ist also $\mathbb{D} = \mathbb{R}\setminus_{\left\{-1;2\right\}}$.

Lösung der Ungleichung:
$\dfrac{x+1}{x^2-x-2} < 0$

Bei dieser Ungleichung ist eine Fallunterscheidung notwendig, da wir mit $\left(x^2-x-2\right)$ multiplizieren müssen.

Fall 1: Wir nehmen an, dass $x^2-x-2 > 0$, also $x < -1$ oder $x > 2$, ist:
$\begin{array}{rclcl}\dfrac{x+1}{x^2-x-2} & < & 0 &\vert & \cdot\left(x^2-x-2\right)\\x+1 & < & 0 &\vert & -1 \\x & < & -1\end{array}$
Der Abgleich der Bedingung $x < -1$ oder $x > 2$ mit dem Ergebnis $x < -1$ führt zu folgender Teillösungsmenge: $\mathbb{L}_1 = \left]-\infty;-1\right[$

Dann noch die Frage: Wie kommt man bei der Bedingung des Falls von $x^2-x-2 > 0$ auf $x < -1$ oder $x > 2$?
Interpretiert man den Nennerterm der Ungleichung als quadratische Funktion $f(x)=x^2-x-2$, so haben wir bei der Bestimmung des Definitionsbereichs deren Nullstellen ermittelt. Da es sich um eine nach oben geöffnete Parabel handelt, müssen die Funktionswerte links von der ersten Nullstelle und rechts von der zweiten Nullstelle positiv sein.

Fall 2: Wir nehmen an, dass $x^2-x-2 < 0$, also $x > -1$ und $x < 2$, ist:

$\begin{array}{rclcl}\dfrac{x+1}{x^2-x-2} & < & 0 &\vert & \cdot\left(x^2-x-2\right)\\x+1 & > & 0 &\vert & -1 \\x & > & -1\end{array}$
Der Abgleich der Bedingung $x > -1$ und $x < 2$ mit dem Ergebnis $x > -1$ führt zu folgender Teillösungsmenge: $\mathbb{L}_2 = \left]-1;2\right[$

Ergebnis: $\mathbb{L}=\mathbb{L}_1 \cup \mathbb{L}_2=\left]-\infty;-1\right[ \cup \left]-1;2\right[$

2. Aufgabe

Allgemeiner Lösungsweg:
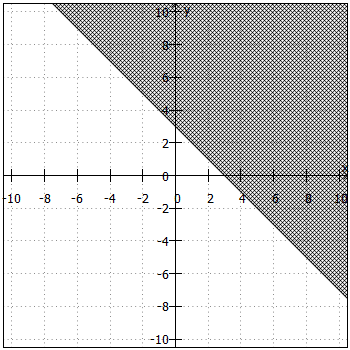
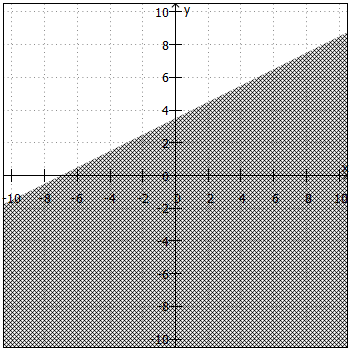
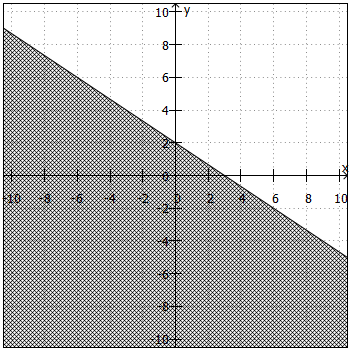
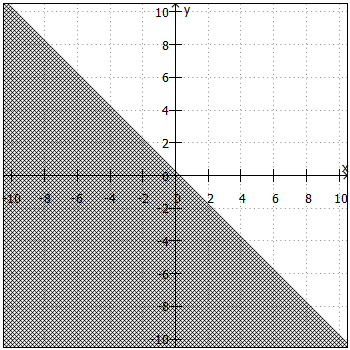
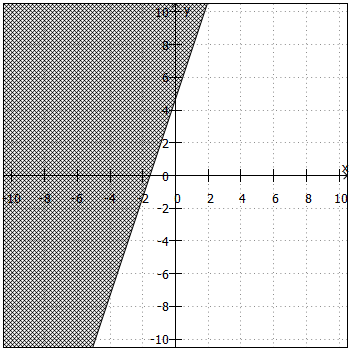
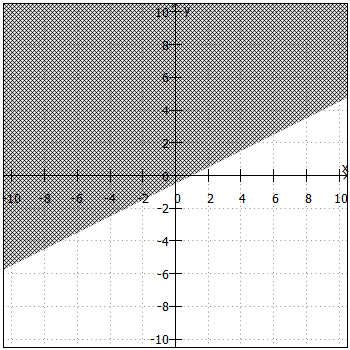
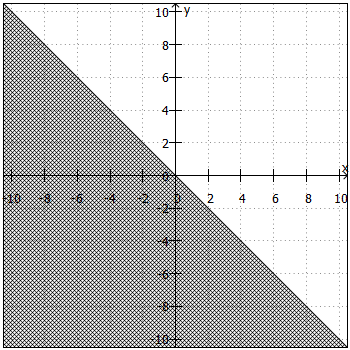
Um die Lösungsmenge in ein Koordinatensystem zeichnen zu können, benötigen wir die Ungleichung zunächst in der Form $y>...$, $y\ge...$, $y < ...$ oder $y\le...$. Daraus ergibt sich die "Trennlinie" zwischen Lösungsmenge und Nicht-Lösungsmenge. Anschließend sind noch folgende Fragen zu klären:

1. Liegt die Lösungsmenge ober- oder unterhalb der "Trennlinie"?
   Bei $>$ und $\ge$ liegt die Lösungsmenge oberhalb, bei $<$ und $\le$ unterhalb der "Trennlinie".
2. Ist die "Trennlinie" teil der Lösungsmenge oder nicht?
   Bei $\ge$ und $\le$ ist die "Trennlinie" teil der Lösungsmenge, bei $>$ und $<$ nicht.

1)
$\begin{array}{rclcl} x+y & \geq & 3 \cr y & \geq & -x+3 \end{array}$

2)
$\begin{array}{rclcl} 2x+5y & \leq & 10 & \vert & -2x \cr 5y & \leq & 10-2x & \vert & :5 \cr y & \leq & -\dfrac{2}{5}x+2 \end{array}$

3)
$\begin{array}{rclcl} -4x-7y & > & -1 & \vert & +4x \cr -7y & > & -1+4x & \vert & :(-7) \cr y & < & -\dfrac{4}{7}x+\dfrac{1}{7} \end{array}$

4)
$\begin{array}{rclcl} 9x-3y & \leq & 24 & \vert & -9x \cr -3y & \leq & 24-9x & \vert & :(-3) \cr y & \geq & 3x-8 \end{array}$

5)
$\begin{array}{rclcl} -5x+10y & < & 35 & \vert & +5x \cr 10y & < & 35+5x & \vert & :10 \cr y & < & \dfrac{1}{2}x+\dfrac{7}{2} \end{array}$

6)
$\begin{array}{rclcl}6x + 9y & \leq & 18 &\vert& -6x \cr 9y & \leq & -6x +18 &\vert& :9 \cr y & \leq & - \dfrac23 x +2\end{array}$

7)
$\begin{array}{rclcl}5y + 3x - 1 & < & 2y &\vert& -2y \cr 3y + 3x - 1 & < & 0 &\vert& -3x+1 \cr 3y & < & - 3x+1 &\vert& :3 \cr y & < & -x +\dfrac13\end{array}$

8)
$\begin{array}{rclcl}\dfrac{y}{3} & \geq & x + \dfrac{14}{9} &\vert& \cdot 3 \cr y & \geq & 3x + \dfrac{14}{3}\end{array}$

9)
$\begin{array}{rclcl}40x + 60 - 80y & < & 100 &\vert& -40x-60 \cr -80y & < & -40x+40 &\vert& :(-80) \cr y &>& \dfrac12 x - \dfrac12\end{array}$

10)
$\begin{array}{rclcl}x + 2y & \leq & -2x - y &\vert& +y-x \cr 3y & \leq & -3x &\vert& :3 \cr y & \leq & -x\end{array}$

3. Aufgabe

Im "Beweis" wurde die Fallunterscheidung vergessen. Bei der Multiplikation mit $-x$ kann keine Aussage darüber getroffen werden, ob mit einer positiven oder negativen Zahl multipliziert wird - und das hat bei Ungleichungen ja Auswirkungen auf die Richtung des Vergleichszeichen. Richtig müsste die Rechnung lauten:

1. Fall: Wir nehmen an, dass $x>0$ ist. Dann ist $-x < 0$:

$\begin{array}{rclcl} x-1 & < & x &\vert&\cdot (-x) \cr -x^2+x &>& -x^2 &\vert& -x^2 \cr x &>& 0 \end{array}$

Das ist nun wirklich nicht spektakulär, denn genau dies hatten wir zu Beginn der Rechnung angenommen.

Bemerkung: Die Multiplikation mit $-x$ ist hier ohne Einschränkungen möglich, weil $-x < 0$. Eine Multiplikation mit $0$ kann also nicht passieren.

2. Fall: Wir nehmen an, dass $x=0$ ist. Diesen Fall müssen wir extra betrachten, weil wir jetzt mit $x$ nicht multiplizieren dürfen:

$\begin{array}{rclcl} x-1 & < & x &\vert& -x \cr -1 & < & 0 \end{array}$

Geht auch klar.

3. Fall: Wir nehmen an, dass $x < 0$ ist. Dann ist $-x>0$:

$\begin{array}{rclcl} x-1 & < & x &\vert&\cdot (-x) \cr -x^2+x & < & -x^2 &\vert& -x^2 \cr x & < & 0 \end{array}$

Bemerkung: Die Multiplikation mit $-x$ ist hier ohne Einschränkungen möglich, weil $-x > 0$. Eine Multiplikation mit $0$ kann also nicht passieren.

Das ist zwar die gleiche Rechnung, wie im "Beweis" auf der Aufgabenseite; mit der Zusatzinformation, dass wir hier von vorneherein nur Zahlen kleiner als $0$ betrachten, erscheint die Aussage aber in einem ganz anderen Licht ...

Zusammenfassend stellen wir fest: Unterscheidet man alle Fälle ordentlich, ergeben sich drei recht belanglose Aussagen. Komische Ergebnisse treten nicht auf.

Wesentlich geschickter: Man lässt das Multiplizieren mit $-x$ sein und subtrahiert $x$ stattdessen lieber. Dann steht da nämlich ganz schnell $-1 < 0$ , was sicherlich niemand infrage stellen wird. Mehr Ergebnis bekommen wir hier nicht, was auch nicht so überraschend ist, denn die Aussage, mit der wir in den "Beweis" gestartet waren, war ja nicht sehr gehaltvoll ...