SOS Mathematik
Übersicht:
25.3 Komplexe Zahlen - Lösungen
1. Aufgabe
Bemerkung: Bei den folgenden Lösungen wurde das Gradmaß verwendet, weil sich keine "vernünftigen" Vielfache von ergeben.
1)
Betrag:
Argument:
Daraus ergibt sich folgendes:
Trigonometrische Darstellung:
Exponentielle Darstellung:
2)
Betrag:
Argument:
Daraus ergibt sich folgendes:
Trigonometrische Darstellung:
Exponentielle Darstellung:
3)
Betrag:
Argument:
Daraus ergibt sich folgendes:
Trigonometrische Darstellung:
Exponentielle Darstellung:
4)
Betrag:
Argument:
Daraus ergibt sich folgendes:
Trigonometrische Darstellung:
Exponentielle Darstellung:
5)
Betrag:
Argument:
Daraus ergibt sich folgendes:
Trigonometrische Darstellung:
Exponentielle Darstellung:
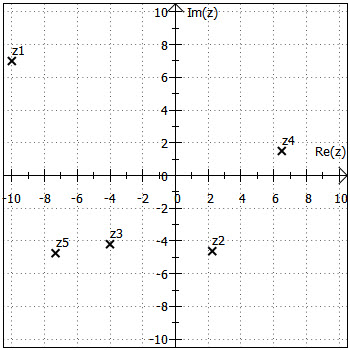
6)
Die exponentielle Form lässt sich ohne Rechnen ermitteln, nämlich:
Für die kartesische Form ergibt sich und
und daraus
7)
Die exponentielle Form lässt sich ohne Rechnen ermitteln, nämlich:
Für die kartesische Form ergibt sich und
und daraus
8)
Die exponentielle Form lässt sich ohne Rechnen ermitteln, nämlich:
Für die kartesische Form ergibt sich und
und daraus
9)
Die exponentielle Form lässt sich ohne Rechnen ermitteln, nämlich:
Für die kartesische Form ergibt sich und
und daraus
10)
Die exponentielle Form lässt sich ohne Rechnen ermitteln, nämlich:
Für die kartesische Form ergibt sich und
und daraus
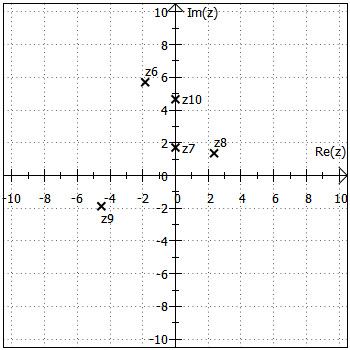
11)
Hier kann man die trigonometrische Form quasi ablesen:
Für die kartesische Form berechnet man und
und erhält damit
12)
Hier kann man die trigonometrische Form quasi ablesen:
Für die kartesische Form berechnet man: und
und erhält damit
13)
Hier kann man die trigonometrische Form quasi ablesen:
Für die kartesische Form berechnet man: und
und erhält damit
14)
Hier kann man die trigonometrische Form quasi ablesen:
Für die kartesische Form berechnet man: und
und erhält damit
15)
Hier kann man die trigonometrische Form quasi ablesen:
Für die kartesische Form berechnet man: und
und erhält damit
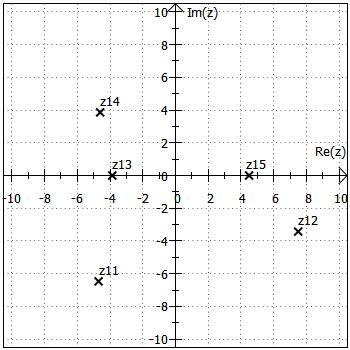
2. Aufgabe
Hinweis 1: Basale Umformungen, wie das Erweitern und Kürzen von Brüchen, das Zusammenfassen von Zahlenwerten, das Auflösen von Klammern etc. wurde hier nicht mehr extra aufgeschrieben und ausgewiesen. Bitte denken Sie daran, dass die "normalen" Regeln der Bruchrechnung auch hier gelten!
Hinweis 2: Auch hier gilt (nach wie vor) "Potenz- vor Punkt- vor Strichrechnung". Das bedeutet zum Beispiel: und
lassen sich nicht zusammenfassen!
a)
10)
Bemerkung: Bei der letzten Umformung wurde zusätzlich gekürzt.
b)
Bemerkung 1: Für diese Aufgaben benötigt man den Satz von de Moivre.
Bemerkung 2: Bitte beachten Sie, dass bei einigen Aufgaben eine letzte Umformung nötig wird, weil laut Aufgabenstellung gefordert ist, dass .
3. Aufgabe
Bemerkung: Auch hier werden einige letzte Umformungen nötig, weil gefordert ist, dass .
1)
4)
Bemerkung: Für die letzte Umformung wurde die eulersche Identität verwendet.
4. Aufgabe
Bemerkung: Es gibt absichtlich keine umfangreichen Erklärungen zu diesen Aufgaben, denn Gleichungen bleiben Gleichungen und komplexe Zahlen sind in erster Linie einmal Zahlen und erst in zweiter Linie komplex. Insofern ist hier vorab nicht viel zu sagen. Rechnen Sie einfach drauf los!
Wer Schwierigkeiten hat, schaue in den Kapiteln Quadratische Gleichungen bzw. Polynome nach.
1)
4)
Bemerkung: Bislang war der Satz vom Nullprodukt zwar immer so formuliert worden: "Ein Produkt reeller Zahlen ist genau dann , wenn einer der Faktoren
ist." Er gilt aber natürlich auch für komplexe Zahlen.
5)
Bemerkung: ist eine doppelte Lösung.
6)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
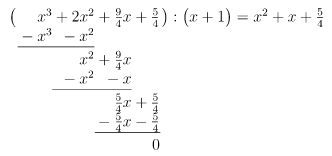
Lösung des reduzierten Polynoms:
10)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
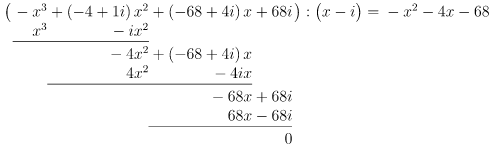
Lösung des reduzierten Polynoms:
11)
Substitution:
Rücksubstitution:
12)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
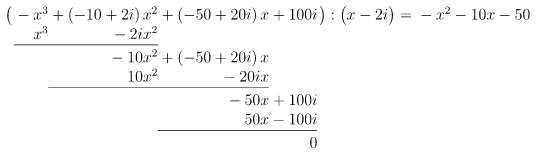
Lösung des reduzierten Polynoms:
14)
Bemerkung: Die Multiplikation mit ist hier ohne Einschränkungen möglich, weil
. Eine Multiplikation mit
kann also nicht passieren.
16)
allgemeine Formel für die Wurzeln aus einer komplexen Zahl:
Bestimmung von und
:
Da und
ist
.
Berechnung der Wurzeln:
17)
allgemeine Formel für die Wurzeln aus einer komplexen Zahl:
Bestimmung von und
:
Da und
ist
.
Berechnung der Wurzeln:
18)
allgemeine Formel für die Wurzeln aus einer komplexen Zahl:
Bestimmung von und
:
Da und
ist
.
Berechnung der Wurzeln:
19)
allgemeine Formel für die Wurzeln aus einer komplexen Zahl:
Bestimmung von und
:
Da und
liegt
im zweiten Quadranten.
Berechnung der Wurzeln:
20)
allgemeine Formel für die Wurzeln aus einer komplexen Zahl:
Bestimmung von und
:
Da und
liegt
im dritten Quadranten.
Berechnung der Wurzeln: