SOS Mathematik
Übersicht:
18.3 Betragsgleichungen und -funktionen - Lösungen
Eine Bemerkung vorab: Verschachtelte Funktionen betrachtet man am besten von innen nach außen.
1. Aufgabe
1)
Bei handelt es sich um eine um
nach oben verschobene Wurzelfunktion.
hat keine Nullstellen, weil
und deswegen
für alle
. Bei
hat
ein Minimum, denn
ist kleiner als
für alle anderen
.
Für den Wertebereich gilt:
2)
Der Funktionsterm lässt sich vereinfachen zu , weil
. Es handelt sich hierbei also um eine gebrochen rationale Funktion, deren Graph eine Hyperbel ungerader Ordnung ist. Wegen des Faktors
im Zähler verläuft der Graph nicht durch die Punkte
und
sondern durch
und
.
hat eine Polstelle bei
.
ist punktsymmetrisch zum Koordinatenursprung.
3)
Diese Funktion ist linear; ihr Graph ist also eine Gerade. Der Betrag bewirkt nur, dass der Koeffizient positiv wird. Es handelt sich bei also um eine steigende Gerade, deren Funktionsgleichung man auch einfacher als
schreiben könnte. Da keine Konstante addiert wird, handelt es sich um eine Ursprungsgerade, die logischerweise eine Nullstelle bei
hat.
ist punktsymmetrisch zum Koordinatenursprung.
4)
Der Graph von ist eine um
nach rechts verschobene Hyperbel ungerader Ordnung. Aufgrund der Verschiebung und des Faktors
im Zähler verläuft der Graph von
durch die Punkte
und
statt durch
und
.
Die Funktion hat bei
eine Polstelle.
ist punktsymmetrisch zum Punkt
.
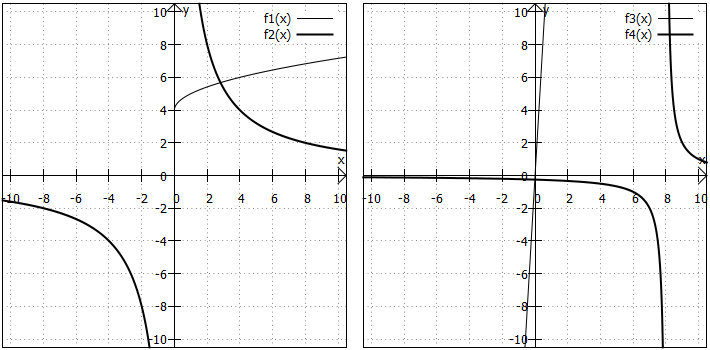
5)
Der Betrag hat bei dieser Funktion keine Wirkung, da ohnehin immer positiv ist. Der Graph ist also eine Hyperbel gerader Ordnung, die (wie das solche einfachen Hyperbeln gerader Ordnung nun mal tun) durch die Punkte
und
verläuft.
hat eine Polstelle bei
.
Der Graph ist achsensymmetrisch zur y-Achse.
6)
Durch den Betrag im Radikanden können hier alle reellen Zahlen eingesetzt werden. Für negative Zahlen verläuft die Funktion analog zum positiven Bereich. hat eine Nullstelle bei
, die zugleich Minimum der Funktion ist. Kleiner als
kann das Ergebnis einer Wurzel ja nicht werden. Daran ändert auch der Betrag im Radikanden nichts.
Der Graph ist achsensymmetrisch zur y-Achse, daher verläuft der Graph nicht nur durch den Punkt , wie das für solche Wurzelfunktionen üblich ist, sondern auch durch
.
7) ist eine um
nach oben verschobene nach unten geöffnete Betragsfunktion.
Die Funktion hat Nullstellen bei und
und ein Maximum bei
, weil
für alle
. Also ist
dann am größten, wenn
ist. Dann wird nämlich am wenigsten von der
subtrahiert.
ist achsensymmetrisch zur y-Achse.
Für den Wertebereich gilt:
8)
Vereinfacht gilt: . Der Graph dieser Funktion verläuft wie der positive Ast einer Hyperbel. Wegen
und des Faktors
im Zähler verläuft der Graph durch den Punkt
.
hat eine Polstelle bei
.
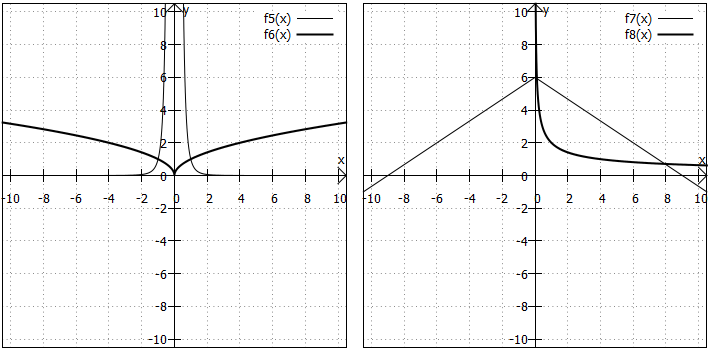
9)
Innerhalb des Betrags steht der Term einer um nach oben und um
nach links verschobenen Hyperbel ungerader Ordnung. Der Betrag bewirkt nun, dass alle Punkte mit negativem Funktionswert "nach oben geklappt" werden. Der Graph von
verläuft aufgrund der Verschiebung durch die Punkte
und
. Da diese Punkte ohnehin positive Funktionswerte haben, ändert der Betrag hier also nichts.
hat eine Nullstelle bei
, die gleichzeitig Minimum ist, weil
und
hier der kleinste mögliche Wert ist. Bei
liegt eine Polstelle. Für sehr große und sehr kleine x-Werte nähern sich die Funktionswerte der
an.
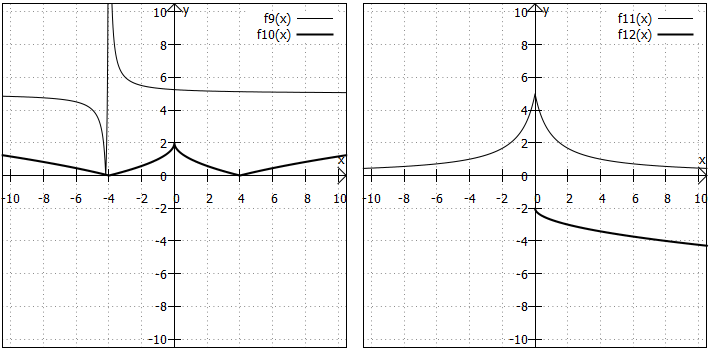
10)
Zunächst steht unter der Wurzel die Variable innerhalb eines Betrags. Das bewirkt, dass die Funktion für alle reellen Zahlen definiert ist, weil die Variable unter der Wurzel nie negativ werden kann. Innerhalb des äußeren Betrags steht also der Term dieser Wurzelfunktion um nach unten verschoben. Der Betrag bewirkt nun, dass alle Punkte mit negativem Funktionswert "nach oben geklappt" werden.
hat zwei Nullstellen bei
und bei
, die gleichzeitig Minima sind. Kleiner als
kann eine solche Betragsfunktion ja nicht werden. Zwischen den zwei Minima muss sich ein Maximum befinden. Da die Funktion aufgrund des Betrages achsensymmetrisch ist, muss das Maximum genau "in der Mitte" zwischen den Minima liegen. Es liegt also bei
.
11)
Die Funktion hat ein Maximum bei , weil der Nenner dort am kleinsten ist. Je größer
wird, desto größer wird der Nenner und desto kleiner wird der Wert des gesamten Bruches. Gleiches gilt für sehr kleine
, da das Vorzeichen wegen des Betrages irrelevant ist. An beiden Rändern des Definitionsbereiches nähert sich der Graph von
also der
an.
Da niemals
werden kann, wird der Nenner nie
. Es gibt also keine Definitionslücken.
ist aufgrund des Betrages achsensymmetrisch.
Für den Wertebereich gilt:
12)
Die Funktion ist eine "nach unten gekippte" Wurzelfunktion. Zusätzlich ist sie um nach unten verschoben.
hat ein Maximum bei
, denn dort ist der Radikand
. Es wird bei
also nichts von der
subtrahiert, sodass der Funktionswert hier am größten ist.
Für den Wertebereich gilt:
2. Aufgabe
1)
a)
b)
Probe:
Für :
Für :
Ergebnis: Für und
ergeben sich wahre Aussagen:
und
sind also tatsächlich Punkte des Graphen.
2)
a)
b)
Probe:
Für :
Für :
Ergebnis: Für und
ergeben sich wahre Aussagen:
und
sind also tatsächlich Punkte des Graphen.
3)
a)
b)
Probe:
Für :
Für :
Ergebnis: Für und
ergeben sich wahre Aussagen:
und
sind also tatsächlich Punkte des Graphen.
4)
a)
b)
Substitution:
Rücksubstitution:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert die Rücksubstitution von keine weiteren Punkte.
Probe:
Für :
Für :
Ergebnis: Für und
ergeben sich unwahre Aussagen:
und
sind also nicht Lösungen der Gleichung. Das bedeutet, dass die Funktion nirgends den Funktionswert
annimmt.
5)
a)
b)
Probe:
Für :
Für :
Ergebnis: Für und
ergeben sich wahre Aussagen:
und
sind also tatsächlich Punkte des Graphen.
6)
a)
b) ist keine Lösung, da im ersten Fall nur
infrage kommen. Ebenso ist
keine Lösung, da im zweiten Fall nur
möglich sind.
Probe:
Für :
Für :
Ergebnis: Für und
ergeben sich wahre Aussagen:
und
sind also tatsächlich Punkte des Graphen.
7)
a)
b)
Bemerkung: Da der Betrag sein soll, können wir den Betragsstriche weglassen (Umformung von der 3. zur 4. Zeile), da
ja weder positiv noch negativ ist.
Probe:
Für :
Für :
Ergebnis: Für und
ergeben sich wahre Aussagen:
und
sind also tatsächlich Punkte des Graphen.
8)
a)
b) ist keine Lösung, da im ersten Fall nur
infrage kommen. Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert der zweite Fall keine weiteren Punkte.
Probe:
Für :
Ergebnis: Für ergibt sich eine wahre Aussage:
ist also tatsächlich ein Punkt des Graphen.
9)
a)
b) ist keine Lösung, da im ersten Fall nur
infrage kommen. Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert der zweite Fall keine weiteren Punkte.
Probe:
Für :
Ergebnis: Für ergibt sich eine wahre Aussage:
ist also tatsächlich ein Punkt des Graphen.
10)
a)
b)
Bemerkung: Da der Betrag sein soll, können wir den Betragsstriche weglassen (Umformung von der 3. zur 4. Zeile), da
ja weder positiv noch negativ ist.
Probe:
Für :
Für :
Ergebnis: Für und
sich wahre Aussagen:
und
sind also tatsächlich Punkte des Graphen.
3. Aufgabe
Im ersten Koordinatensystem ist die Funktion zu sehen, also eine klassische Polynomfunktion. Um genau zu sein, handelt es sich hierbei um ein biquadratisches Polynom. Die Funktionswerte im Intervall
sind hier auch ohne Betrag positiv, was man z. B. sehen kann, wenn man
berechnet.
Im zweiten Koordinatensystem ist die Funktion dargestellt. Im Gegensatz zu Polynomfunktionen können Betragsfunktionen "Knicke" enthalten, nämlich immer dort, wo die Funktionswerte, wenn man die Funktion ohne den Betrag betrachtet, das Vorzeichen wechseln. Die Funktionswerte im Intervall
sind hier nur deswegen positiv, weil der Betrag auf
angewendet wird, sonst wären sie negativ. Das sieht man z. B., wenn man
berechnet. Ohne den Betrag wäre der Graph von
eine ganz normale nach oben geöffnete Parabel mit einem Tiefpunkt bei
.