SOS Mathematik
Übersicht:
12.3 Eigenschaften und "besondere Punkte" von Funktionen - Lösungen
1. Aufgabe
1)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist punktsymmetrisch zum Koordinatenursprung.
2)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
3)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist punktsymmetrisch zum Koordinatenursprung.
4)
Die Funktion ist achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
5)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
6)
Die Funktion ist achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
7)
Die Funktion ist achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
8)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist punktsymmetrisch zum Koordinatenursprung.
9)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
10)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
11)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
12)
Die Funktion ist achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
13)
Die Funktion ist achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
Bemerkung: Bitte achten Sie darauf, dass die Variable hier heißt und nicht
.
14)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
15)
Die Funktion ist achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
16)
Die Funktion ist achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
17)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist punktsymmetrisch zum Koordinatenursprung.
18)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
19)
Die Funktion ist achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
20)
Die Funktion ist nicht achsensymmetrisch zur y-Achse.
Die Funktion ist nicht punktsymmetrisch zum Koordinatenursprung.
Zusatzfrage: Es gibt eine Funktion, die sowohl achsensymmetrisch zur y-Achse als auch punktsymmetrisch zum Koordinatenursprung ist, nämlich .
Ok, keine besonders spannende Funktion ...
2. Aufgabe
1)
Beide Werte liegen im Definitionsbereich, daher sind und
tatsächlich Nullstellen der Funktion.
2)
Dies ist keine Nullstelle der Funktion, denn .
3)
Dieser Wert liegt im Definitionsbereich, daher ist tatsächlich Nullstelle der Funktion.
4)
Von diesen Werten liegen nur und
im Definitionsbereich, daher sind auch nur an diesen Stellen tatsächlich Nullstellen der Funktion.
5)
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Funktion keine Nullstellen.
3. Aufgabe
1)
Dies ist eine lineare Funktion. Wenn man mal von konstanten Funktionen absieht, können lineare Funktionen entweder ausschließlich ansteigend oder ausschließlich fallend sein. Mischformen gibt es nicht. Extrempunkte können also allenfalls an den Rändern des Definitionsbereichs entstehen. Sind solche Funktionen, wie bei dieser Aufgabe, für die gesamten reellen Zahlen definiert, haben sie keine Extrempunkte.
Bemerkung: und
sind keine Zahlen, daher können dort auch keine Extrempunkte vorliegen.
2)
Quadratische Funktionen haben im Scheitelpunkt entweder einen Tiefpunkt (wenn die Parabel nach oben geöffnet ist) oder einen Hochpunkt (wenn die Parabel nach unten geöffnet ist). Den Scheitelpunkt kann man z. B. mithilfe der quadratischen Ergänzung bestimmen:
Da ist, liegt der Scheitelpunkt der Funktion also bei
. Da die Parabel nach oben geöffnet ist (vor dem
-Term steht eine positive Zahl, nämlich
), kann im Scheitelpunkt nur ein Tiefpunkt liegen.
Interessant ist noch der obere Rand des Definitionsbereichs, nämlich die Stelle . Da es sich um eine nach oben geöffnete Parabel handelt und der Tiefpunkt bei
liegt, ist die Funktion bei
ansteigend. Bei
liegt also ein Hochpunkt.
3)
Dies ist wieder eine lineare Funktion. Im Gegensatz zu 1) ist sie aber nur für einen Teilbereich der reellen Zahlen definiert, nämlich für . In diesem Fall liegt am unteren Ende des Definitionsbereichs ein Extrempunkt vor. Da die Steigung hier positiv ist, muss der Wert am unteren Ende des Definitionsbereichs der kleinste Funktionswert von allen sein. Es liegt also ein Tiefpunkt bei
vor.
4)
Diese Funktion ist konstant. Daher kann sie keinen größten oder kleinsten Wert haben.
5) lässt sich durch Ausklammern von
und mithilfe der 2. binomischen Formel auf folgende Form bringen:
. Daran kann man 1. ablesen, dass die Funktion nach unten geöffnet ist (vor dem
-Term steht eine negative Zahl), und 2., dass die Funktion im Punkt
ihren Scheitelpunkt hat. Es gilt aber:
. Daher liegt hier kein Extrempunkt der Funktion vor.
Es müssen nun noch die Ränder des Definitionsbereichs betrachtet werden: Bei liegt ein Tiefpunkt und bei
ein Hochpunkt der Funktion, da
als nach unten geöffnete Parabel mit einem Scheitelpunkt bei
bis
ansteigend ist.
6)
Dies ist eine fallende lineare Funktion, die nur für einen Teilbereich der reellen Zahlen definiert ist, nämlich für . Ein Extrempunkt kann daher nur am unteren Rand des Definitionsbereiches auftreten. Der dazu gehörige Funktionswert kann dann einfach berechnet werden:
. Da die Funktion fällt, ist es ein Hochpunkt.
7)
Hier liegt eine quadratische Funktion vor, die nach oben geöffnet ist (der Koeffizient vor ist ja positiv). Es ist also ein Tiefpunkt zu erwarten. Der Scheitelpunkt wird mit Hilfe der quadratischen Ergänzung bestimmt:
Der Scheitelpunkt liegt also bei .
Da die Funktion in dieser Aufgabe für die gesamten reellen Zahlen definiert ist, können an den Rändern des Definitionsbereiches keine weiteren Extrempunkte existieren.
8)
Hierbei handelt es sich wieder um eine lineare Funktion. Da der Definitionsbereich alle reellen Zahlen umfasst, kann in diesem Fall nirgends ein Extrempunkt auftreten.
9)
Hier haben wir es wieder mit einer steigenden linearen Funktion mit einem eingeschränkten Definitionsbereich zu tun. Da der Definitionsbereich aber auf ein offenes Intervall eingeschränkt ist, gibt es keine Randwerte, an denen Extrempunkte auftreten können.
10)
Hierbei handelt es sich um eine nach unten geöffnete quadratische Funktion, die um den Faktor gestreckt und um
Einheiten nach oben verschoben ist. Da keine Verschiebung nach links/recht erfolgt, muss der Scheitelpunkt also bei
liegen. Es handelt sich um einen Hochpunkt, da die Parabel nach unten geöffnet ist. Deshalb treten auch an den Grenzen des Definitionsbereiches jeweils Tiefpunkte auf. Die Funktionswerte lassen sich wie folgt berechnen:
Insgesamt hat die Funktion innerhalb der Grenzen des Definitionsbereiches also einen Tiefpunkt bei , einen Hochpunkt bei
und einen weiteren Tiefpunkt bei
.
4. Aufgabe
In den ersten Grafik gibt es folgende Wende- und Sattelpunkte zu entdecken:
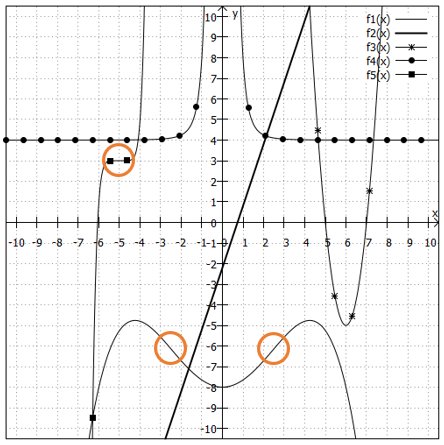
Nicht gefragt waren die konkreten Koordinaten, bei denen die Wende- und Sattelpunkte liegen. Diese können nämlich nur mithilfe von Ableitungen ermittelt werden, was in diesem Lernmodul noch nicht thematisiert wurde. Der Vollständigkeit halber hier noch die Werte:
hat zwei Wendepunkte, die bei
und
liegen.
hat einen Sattelpunkt bei
.
- Die anderen Funktionen in der ersten Grafik haben keine Wende- oder Sattelpunkte.
In der zweiten Grafik finden sich folgende Wende- und Sattelpunkte:
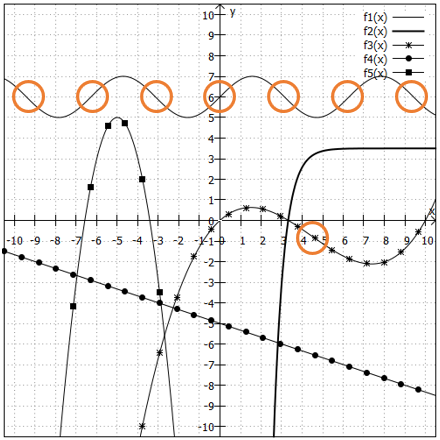
Auch hier noch die konkreten Werte der Wendepunkte: