SOS Mathematik
Dieses Kapitel enthält die folgenden Themen:
14.2 Bruchgleichungen und gebrochen rationale Funktionen - Erklärungen
Dieses Kapitel zeigt einen weiteren Gleichungs- bzw. Funktionstyp, nämlich Gleichungen/Funktionen, in denen Polynome durcheinander dividiert werden. Ein Anwendungsfall für solche Gleichungen und Funktionen sind antiproportionale Zusammenhänge: Beispielsweise berechnet sich die Geschwindigkeit bekanntermaßen nach der Gleichung . Wenn die Geschwindigkeit
in Abhängigkeit der Strecke
bei festgelegter Zeit
berechnet werden soll, steht die Variable im Zähler - das kennen wir schon. Soll hingegen die Geschwindigkeit
in Abhängigkeit der Zeit
bei festgelegter Strecke
berechnet werden soll, steht die Variable im Nenner - darum werden wir uns in diesem Kapitel kümmern. Auch in den Wirtschaftswissenschaften gibt es Zusammenhänge, bei denen die Variable im Nenner des Funktionsterms steht, z. B. sogenannte "regressive Kostenfunktionen". Dabei handelt es sich um Kostenfunktionen, bei denen die Kosten/Stückkosten bei steigender Menge der Bezugsgrößen abnehmen.
Warum die Gleichungen dabei "Bruchgleichungen" und die Funktionen "gebrochen rational" heißen, kann ich Ihnen leider auch nicht sagen ...
Definition
Definition einer Bruchgleichung: Bruchgleichungen sind Gleichungen, bei denen die Variable im Nenner eines Bruchs steht.
Definition einer gebrochen rationalen Funktion: Gebrochen rationale Funktionen sind Funktionen, bei denen die Variable im Nenner eines Bruchs steht.
Anders formuliert: Eine Bruchgleichung/gebrochen rationale Funktion ist ein Quotient zweier Polynome, wobei der Grad des Polynoms im Nenner mindestens sein muss.
Das Polynom im Zähler nennt man Zählerpolynom. Den Grad des Zählerpolynoms nennt man Zählergrad.
Das Polynom im Nenner nennt man Nennerpolynom. Den Grad des Nennerpolynoms nennt man Nennergrad.
Natürlich darf eine Bruchgleichung/gebrochen rationale Funktion auch mehrere Brüche enthalten, bei denen Variablen im Nenner stehen. Auch Brüche, bei denen die Variable im Zähler steht, sind erlaubt. Allerdings: Enthält eine Gleichung/Funktion nur Brüche, deren Nenner ausschließlich Zahlen enthalten, benötigen wir keinen neuen Funktions- und Gleichungstyp. Dann kämen wir mit linearen, quadratischen und Polynomgleichungen aus.
Definitionsbereich: Bei Bruchgleichungen/gebrochen rationalen Funktionen ist es wichtig, sich Gedanken zum Definitionsbereich zu machen: Da wir durch nicht teilen dürfen, darf der Nenner niemals den Wert
annehmen. Wir müssen also prüfen, für welche Variablenwerte das passiert, und den Definitionsbereich so "zuschneiden", dass nur passende Werte enthalten sind. Dafür müssen Ungleichungen gelöst werden.
Wichtig: Der Definitionsbereich gehört fest zu Gleichungen/Funktionen dazu.
Das Umformen des Bruchterms, z. B. durch Kürzen, kann daher problematisch sein. Ein Beispiel: Die Funktion ist nicht identisch mit der Funktion
. Denn: Der Definitionsbereich von
ist
; der Definitionsbereich von
ist
. Diese Veränderung darf nicht einfach so "unter den Tisch fallen". Weitere Erläuterungen dazu gibt es ganz unten in diesem Kapitel bei der Beispielfunktion
.
Bruchgleichungen
Starten wir auch hier wieder mit einigen Beispielen:
mit
mit
mit
Da der Nenner des ersten Bruchs mithilfe der 3. binomischen Formel umgeformt werden kann zu, gibt es nur zwei Variablenwerte, für die einer der Nenner
wird.
Lösungsweg
Bei Bruchgleichungen ist es immer das erste Ziel, die Brüche aus der Gleichung zu entfernen. Dann entstehen nämlich häufig lineare oder quadratische Gleichungen, von denen wir schon wissen, wie man sie löst. Das ist ein ganz typisches Vorgehen, wenn in der Mathematik neue Probleme auftauchen: Man versucht, das Problem so zu bearbeiten, dass etwas Bekanntes entsteht, wo man schon Lösungswege kennt. Dann muss man sich für den Rest keine weiteren Gedanken machen.
Für Bruchgleichungen bedeutet das, dass wir die gesamte Gleichung mit den enthaltenen Nennern multiplizieren müssen, wenn die Nenner Variablen enthalten. Sie erinnern sich, was passiert, wenn man einen Bruch mit seinem Nenner multipliziert? Richtig: Die Nenner kürzen sich gegenseitig weg, wie bei
Ganz wichtig: Auch bei Bruchgleichungen darf man natürlich nicht aus Summen und ebenso nicht aus Potenzen mit unterschiedlichen Basen kürzen!
Zum Abschluss des Lösungsweges muss noch zwingend überprüft werden, ob sich alle ermittelten Werte für die Variable im Definitionsbereich befinden. Werte, die nicht im Definitionsbereich liegen, stellen keine Lösungen für die ursprüngliche Gleichung dar. Man bezeichnet sie daher als Scheinlösungen. Was genau das ist, wird weiter unten erklärt.
Schauen wir uns nun einige Beispiele an:
Beispiel 1:
Betrachten wir die Gleichung .
Bestimmung des Definitionsbereichs:
Die beiden Nenner und
müssen ungleich
sein. Daher müssen wir nun ausrechnen, für welche x-Werte diese Bedingung erfüllt wird:
Aus der Betrachtung der beiden Ergebnisse können wir ableiten, dass wir alle Werte aus mit Ausnahme von
und
verwenden dürfen. Der Definitionsbereich ist also
.
Lösung der Gleichung:
Zur 1. Zeile: Um die Brüche in der Gleichung zu eliminieren, wird zunächst mit multipliziert. Dadurch verschwindet der Bruch auf der linken Seite. Wichtig: Alle Terme der Gleichung müssen mit dem
multipliziert werden! Ebenso wie beim Multiplizieren einer Gleichung mit einer Zahl alle Bestandteile der Gleichung mit dieser Zahl multipliziert werden müssen, ist dies auch beim Multiplizieren mit einem Nenner notwendig. Andernfalls können die Probleme auftreten, die bereits im Kapitel lineare Gleichungen erläutert wurden.
Zur 2. Zeile: Analog zur 1. Zeile soll jetzt der Bruch auf der rechten Seite verschwinden. Daher wird mit dem Nenner des Bruches, also mit multipliziert. Auch hier müssen alle Terme mit dem Faktor durchmultipliziert werden! Zusätzlich wichtig: Da hier mit einer Summe multipliziert wird, müssen Klammern darum gesetzt werden. Sonst kommen Punkt- und Strichrechnung durcheinander ...
Zur 3. Zeile: Der letzte Bruch der Gleichung ist . Diesen Bruch könnte man stehen lassen. Da
ja "nur" eine Zahl ist, würde er beim restlichen Lösungsweg nicht weiter stören. Wenn man alle Terme mit
multipliziert, wie wir das hier gemacht haben, kann man komplett ohne Brüche weiterrechnen.
Ab der 4. Zeile: Nachdem nun alle Brüche entfernt wurden, können die Klammern ausmultipliziert und anschließend die Terme zusammengefasst werden - so wie man das bei jeder anderen Gleichung auch tun würde. Das Ergebnis ist eine quadratische Gleichung, welche mit der p-q-Formel oder der a-b-c-Formel gelöst werden kann.
Zum Abschluss: Beide berechneten Werte liegen im Definitionsbereich und sind also Lösungen der Gleichung.
In der Erklärung zur 2. Zeile von Beispiel 1 wurde betont, dass Klammern um den Nenner gesetzt werden müssen, da der Nenner aus einer Summe besteht, die mit einem anderen Term multipliziert wird und andernfalls die Rechenoperationen nicht mehr in der richtigen Reihenfolge ausgeführt werden. Schauen wir uns in einem nächsten Beispiel an, was passiert, wenn man die Klammern vergisst.
Beispiel 2:
Betrachten wir die Gleichung .
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Zunächst die korrekte Rechnung mit Probe:
Probe:
Für :
Für :
Für und
ergeben sich wahre Aussagen:
Würde man in der zweiten Zeile dieser Rechnung fälschlicherweise keine Klammern setzen, erhielte man die folgende Rechnung:
Probe für :
Man sieht, dass ohne die Klammern aus der quadratischen Gleichung mit zwei Lösungen eine lineare Gleichung mit nur einer Lösung wird. Setzt man die Lösung der linearen Gleichung in die Ausgangsgleichung ein, geht die Probe nicht auf. Das heißt, die fehlenden Klammern ändern die Rechnung so erheblich, dass der ausgerechnete Wert keine Lösung mehr ist. Daher: Die Klammern müssen also immer gesetzt werden, wenn der Nenner eine Summe/Differenz enthält!
Beispiel 3:
Dass man nicht einfach mit jedem Nenner durchmultiplizieren sollte, sieht man an der folgenden Bruchgleichung .
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
1. Lösung der Gleichung: Zunächst der geschicktere Lösungsweg, bei dem man sich allerdings zuerst die Nenner genau anschauen muss. Dann stellt man nämlich fest, dass der Nenner auf der rechten Seite mithilfe der 1. binomischen Formel zusammengefasst werden kann und das Quadrat des ersten Nenners auf der linken Seite ist (der zweite Nenner links ist ja "nur" eine Zahl und damit eigentlich unerheblich). Man muss also die Gleichung nur mit multiplizieren, um beide Nenner "loszuwerden".
Zur 1. Zeile: Wie oben beschrieben, wird hier der Nenner des Bruchs auf der rechten Seite mithilfe der binomischen Formel zusammengefasst, quasi als Vorbereitung des eigentlichen Lösungsweges.
Zur 2. Zeile: Nun werden auch hier die Brüche eliminiert. Dazu wird die Gleichung mit dem Nenner des rechten Bruches durchmultipliziert.
Zur 3. Zeile: Jetzt sieht man, dass durch Umformung aus der 2. Zeile auch der erste Bruch auf der linken Seite verschwindet, da und
gekürzt werden können. Zudem wird nun mit
multipliziert, um auch den zweiten Bruch auf der linken Seite zu entfernen.
Ab der 4. Zeile: Nun haben wir die Bruchgleichung zu einer quadratischen umgeformt, die wir nach den üblichen Methoden lösen können. Vergessen Sie nicht zu prüfen, ob und
im Definitionsbereich liegen!
2. Lösung der Gleichung: Natürlich kann man auch - ohne die Überlegungen zu den Nennern - einfach mit jedem Nenner multiplizieren. Dann passiert Folgendes:
Zur 1. Zeile: Wir ersparen uns die Vorbereitung des Lösungsweges und multiplizieren sofort mit dem Nenner des linken Bruches.
Zur 2. Zeile: Nun wird die Gleichung mit multipliziert, um den zweiten Bruch auf der linken Seite zu entfernen.
Zur 3. Zeile: Der letzte Bruch der Gleichung befindet sich auf der rechten Seite. Nun wird die Gleichung also mit dessen Nenner multipliziert.
Ab der 4. Zeile: Nun sind alle Brüche aus der Gleichung entfernt und die einzelnen Terme können ausmultipliziert und sortiert werden. Dabei erhält man hier eine kubisches Polynom, also eine Gleichung 3. Grades.
Wenn man die beiden entstehenden Gleichungen und
vergleicht, sieht man schnell, warum es sich lohnt, die Überlegungen zu den Nennern anzustellen. Während die erste relativ problemlos mit der a-b-c-Formel oder der p-q-Formel gelöst werden kann, bleibt bei der zweiten nur, eine Lösung zu erraten und dann eine Polynomdivision durchzuführen. Dazu kommt, dass sich eine dritte Lösung ergibt, die aber nicht im Definitionsbereich der Ausgangsgleichung liegt. Man kann zwar etwas schneller losrechnen, der Lösungsweg wird aber sehr viel komplizierter und damit auch fehleranfälliger.
Nach Abschluss der Rechnung: Prüfung auf Scheinlösungen!
Leider sind nicht alle Gleichungsarten so gutmütig wie lineare und quadratische. Beispielsweise können bei Bruchgleichungen und bestimmten anderen Gleichungstypen sogenannte Scheinlösungen entstehen. Das bedeutet, dass man trotz völlig richtiger Rechnung Werte ausrechnet, die die Ausgangsgleichung doch nicht lösen. Ursache dafür ist, dass uns bestimmte Umformungen im Lösungsweg zwar weiterbringen, sie aber trotzdem die Lösungsmenge ändern können. Mathematisch sagt man: Sie sind keine Äquivalenzumformungen.
Schauen wir uns das am Beispiel an:
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also . Für
würde man ja durch
dividieren, was bekanntermaßen nicht geht.
Lösung der Gleichung:
Multipliziert man die Ausgangsgleichung mit dem Nenner, erhält man die quadratische Gleichung , die die Lösungen
und
hat (Das können Sie selbst ausrechen ...).
Nun kommt das Problem: Die quadratische Gleichung "weiß" nicht, dass es mal einen Nenner gegeben hat ... Dieser Nenner würde werden, wenn wir
einsetzten. Daher hatten wir zu Beginn
aus dem Definitionsbereich ausgeschlossen. Der Wert
kommt als Lösung der Ausgangsgleichung gar nicht infrage.
ist also eine Scheinlösung der Bruchgleichung.
Nur ist wirklich eine Lösung der ursprünglichen Bruchgleichung. Der Definitionsbereich spielt also bei dieser Art von Gleichung eine ziemlich wichtige Rolle. Es muss immer, nachdem die Gleichung gelöst wurde, überprüft werden, ob die berechneten Werte im Definitionsbereich liegen. Dann kann man die Scheinlösungen aus der Lösungsmenge ausschließen. Da Scheinlösungen die ursprüngliche Gleichung ja nicht lösen, haben sie in der Lösungsmenge natürlich nichts zu suchen ... Die Lösungsmenge unserer Beispielgleichung ist demnach:
Sie sehen also, dass das korrekte Rechnen nur ein Teil des richtigen Lösungsweges ist. Noch mal zurück zu den Ausgangsbedingungen und zum Definitionsbereich zu gehen und zu prüfen, ob damit alles in Ordnung ist, ist hier zwingend nötig.
Gebrochen rationale Funktionen
Wir schauen uns den Verlauf und die Eigenschaften von gebrochen rationalen Funktionen zunächst anhand der einfachsten Beispiele, die möglich sind, an. Dabei müssen wir zwei Fälle unterscheiden, weil der Verlauf der Graphen abhängig ist von den Exponenten im Nenner. Als dritter Fall kommen dann Beispiele für komplexere gebrochen rationale Funktionen hinzu.
1. Fall
Im Nenner des Funktionsterms steht nur ein Term und dieser hat einen ungeraden Exponenten, also Funktionen der folgenden Gestalt , wobei
eine ungerade natürliche Zahl ist. Die Graphen nennt man Hyperbeln ungerader Ordnung. Hier einige Beispiele:
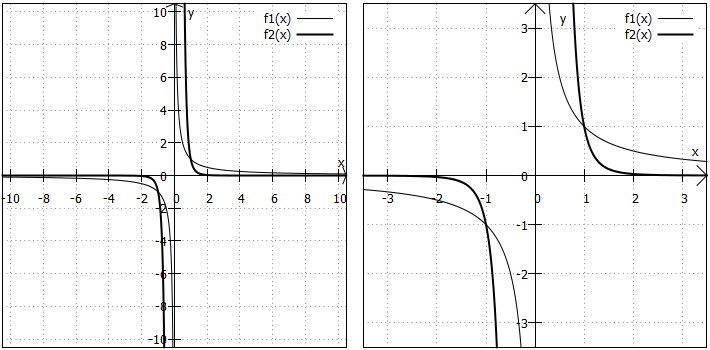
Wertebereich: Der Wertebereich umfasst außer der alle reellen Zahlen.
kann sich ja nicht als Ergebnis einer Division ergeben, wenn
durch eine andere reelle Zahl geteilt wird.
Randverhalten: An den Rändern des Definitionsbereichs nähern sich die Funktionswerte sowohl für sehr kleine als auch für sehr große x-Werte der an.
Symmetrie: Als Funktionen mit ausschließlich ungeraden Exponenten sind ihre Graphen punktsymmetrisch zum Koordinatenursprung.
"Besondere Punkte": Die Hyperbeln haben keine Nullstellen, Extrempunkte und Wendepunkte. Es gibt aber eine Polstelle bei , da die Funktion hier eine Definitionslücke hat. Unmittelbar links von der Definitionslücke werden die Funktionswerte sehr klein und unmittelbar rechts davon werden sie sehr groß.
Weitere Besonderheiten: Alle Funktionsgraphen in diesem Fall verlaufen durch die Punkte und
. Das kann man einfach nachrechnen:
2. Fall
Im Nenner des Funktionsterms steht nur ein Term und dieser hat einen geraden Exponenten, also Funktionen der folgenden Gestalt , wobei
eine gerade natürliche Zahl, außer
, ist. Die Graphen nennt man Hyperbeln gerader Ordnung. Hier einige Beispiele:
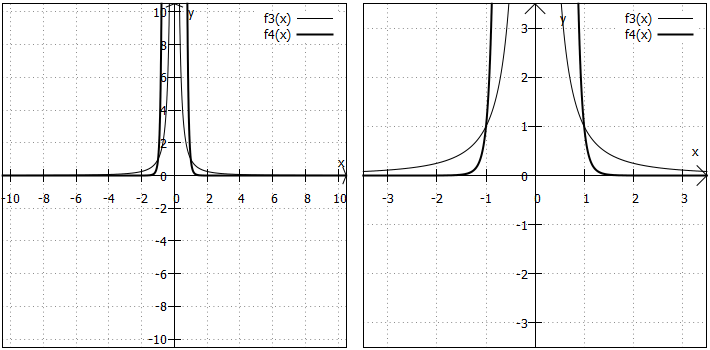
Wertebereich: Der Wertebereich umfasst nur die positiven reellen Zahlen. Egal, welche Zahl für x eingesetzt wird: Da mit einer gerade Zahl potenziert wird, ist der Nenner immer positiv. Und wenn man zwei positive Zahlen durcheinander teilt, muss das Ergebnis ebenfalls positiv sein.
Randverhalten: Die Funktionswerte nähern sich sowohl für sehr kleine als auch für sehr große x-Werte der an.
Symmetrie: Als Funktionen mit ausschließlich geraden Exponenten sind ihre Graphen achsensymmetrisch zur y-Achse.
"Besondere Punkte": Die Hyperbeln haben keine Nullstellen, Extrempunkte und Wendepunkte, aber eine Polstelle bei .
Weitere Besonderheiten: Alle Funktionsgraphen verlaufen durch die Punkte und
. Auch hier kann man das nachrechnen:
3. Fall
Gebrochen rationale Funktionen können aber noch viel mehr. Die Definition erlaubt ja jede Art von Polynom in Zähler und Nenner. Sie werden in den folgenden Grafiken sehen, dass der Verlauf von komplexeren gebrochen rationalen Funktionsgraphen ziemlich unterschiedlich sein kann. Sie heißen dann auch nicht mehr Hyperbeln. Hier einige Beispiele für gebrochen rationale Funktionen allgemeiner Art:

Wertebereich: Der Wertebereich kann sämtliche reellen Zahlen oder nur Teilbereiche von ihnen umfassen. Beispielsweise ist der Wertebereich von nur das halboffene Intervall
.
Randverhalten: Ob sich die Funktionswerte für sehr kleine und sehr große x-Werte der oder einer anderen reellen Zahl annähern oder sehr groß bzw. sehr klein werden, hängt vom Verhältnis von Zähler- zu Nennergrad ab. Um einen Eindruck zu bekommen, wie die Funktion global verläuft, kann man eine Polynomdivision durchführen. Am Beispiel von
:
Wir hatten oben schon gesehen, dass bei einer Polynomdivision ein Rest bleiben kann. Das passiert auch hier. Je größer der Betrag von wird, desto mehr nähert sich der Wert des Rest-Bruches der
an. Für sehr große und sehr kleine x-Werte spielt er also keine Rolle, sodass die Funktion annähernd so verläuft wie die lineare Funktion
. Man nennt dies das asymptotische Verhalten. Zwischen den ganz kleinen und ganz großen x-Werten kann natürlich alles Mögliche passieren (Nullstellen, Extrempunkte, ...). Darüber sagt das asymptotische Verhalten nichts aus.
hat beispielsweise bei
eine Polstelle, was bei linearen Funktionen nicht vorkommen kann.
"Besondere Punkte":
Eine gebrochen rationale Funktion in allgemeiner Form kann Nullstellen haben und zwar an den Nullstellen des Zählerpolynoms. Allerdings muss eine Nullstelle des Zählerpolynoms nicht zwangsläufig eine Nullstelle der gesamten Funktion bewirken (das hängt davon ab, ob das Nennerpolynom bei diesem x-Wert auch eine Nullstelle hat oder nicht).
Ob eine gebrochen rationale Funktion Extrem- und Wendepunkte hat, kann man nicht im Allgemeinen sagen.
Gebrochen rationale Funktionen können an den Nullstellen des Nennerpolynoms (also an den Definitionslücken) Polstellen haben oder auch nicht (das hängt davon ab, ob das Zählerpolynom an dieser Stelle auch eine Nullstelle hat).
Schauen wir uns mit
nochmal etwas genauer an: Sowohl im Zähler als auch im Nenner steht der Faktor
. Daher ist die
auch nicht Element des Definitionsbereichs, ebenso wie die
, die durch den Faktor
ausgeschlossen wird. In der Grafik oben sehen wir aber, dass sich die Funktion bei
und
ganz unterschiedlich verhält: Bei
hat sie eine Polstelle, während bei
auf der ersten Blick gar nichts Auffälliges passiert. Was man auf den ersten Blick nicht sieht, was aber trotzdem da ist, ist eine Definitionslücke bei
, d. h. der Graph hat hier ein "Loch". Daher darf man auch nicht einfach den Faktor
, der in Zähler und Nenner vorkommt, kürzen und den Definitionsbereich anpassen. Das wäre eine andere Funktion! Gleichwohl ist
eine "besondere" Definitionslücke, da bei diesem Wert sowohl im Zähler als auch im Nenner eine Nullstelle auftritt. Man nennt dies eine hebbare Definitionslücke, weil man durch das Kürzen quasi die Definitionslücke "beheben" kann. Man kommt dann zu der neuen Funktion
mit
.