Dieses Kapitel enthält die folgenden Themen:

• Was ist ein Vektor?
• Rechenoperationen mit Vektoren
• Parallelität von Vektoren
• Linearkombinationen von Vektoren
• Der Betrag eines Vektors
• Lineare Unabhängigkeit
• Produkte von Vektoren

 

25.2 Vektorrechnung - Erklärungen

Wie Sie in den letzten Kapiteln ja wahrscheinlich schon gemerkt haben, ist die Mathematik nach den Grundlagenthemen noch lange nicht fertig - im Gegenteil: Sie hat noch viele weitere Konzepte "vorrätig". In diesem Kapitel kommt nun die Unterscheidung zwischen skalaren und vektoriellen Größen hinzu. Das, was Sie bislang kennengelernt haben, sind Skalare gewesen, nämlich Maßzahlen evtl. zusammen mit einer Maßeinheit, z. B. Längen, Zeiten oder Preise. Bei Vektoren kommt - wenn man sie geometrisch interpretiert - zu der Maßzahl noch die Angabe einer Richtung und einer Orientierung hinzu, z. B. bei Geschwindigkeiten oder Kräften. Gerade in der Physik (beispielsweise bei den Bewegungsgleichungen Isaac Newtons) wird das Verstehen schwierig, wenn man nicht weiß, was Vektoren sind und wie man mit ihnen rechnet. Bei wirtschaftlichen Betrachtungen sind Richtung und Orientierung zwar meist eher unwichtig, trotzdem hat sich das Rechnen mit Vektoren hier in vielen Fällen als sinnvoll und praktisch herausgestellt.

Das Wort "Vektor" kommt aus dem Lateinischen und bedeutet "Träger" oder "Passagier"; sprich: Es geht darum, etwas von einem Ort zu einem anderen zu transportieren, was dem gerade beschriebenen physikalischen Verständnis von Vektoren nahe kommt. Das Wort "Skalar" stammt - ebenso wie "Skala" und "Skalierung" - vom lateinischen Wort "scala" ab, welches "Leiter" oder "Treppe" bedeutet. Skalare lassen sich also wie Treppenstufen anordnen. Dass man in der Vektorrechnung lieber "Skalar" statt einfach "Zahl" sagt, hat u. a. damit zu tun, dass sie sich dadurch leichter von den Zahlen im Vektor, die ja eine ganz andere "Aufgabe" haben, unterscheiden lassen.

 

Was ist ein Vektor?

Es gibt viele Varianten, einen Vektor zu beschreiben: Die Spanne reicht von der mathematisch-theoretischen Denkweise, in der ein Vektor ein "Repräsentant eines Vektorraumes" ist, bis zur anschaulichen Beschreibung eines Vektors als Pfeil. Wir nutzen in diesem Kapitel zwei Definitionen eines Vektors:

Komponentenweise: Ein Vektor ist ein n-Tupel reeller (oder auch komplexer) Zahlen. Diese Zahlen nennt man die Komponenten des Vektors. Man kann mithilfe eines Vektors also mehrere Zahlen zu einem (mathematischen) Objekt zusammenfassen und damit rechnen. In dieser Hinsicht haben Vektoren eine gewisse Ähnlichkeit mit Tabellen, die ja auch strukturierte Zusammenstellungen von Zahlenwerten sind.
Man unterscheidet dabei Zeilenvektoren $\vec{a}^{\,T}=\begin{pmatrix} a_1;\, a_2;\, \ldots;\, a_n\end{pmatrix}$ und Spaltenvektoren $\vec{a}=\begin{pmatrix}a_1\cr a_2\cr\ldots\cr a_n\end{pmatrix}$. Um einen Zeilenvektor zu kennzeichnen, verwendet man das hochgestellte $T$, welches für transponiert steht und Zeilen und Spalten gegeneinander tauscht. Für die geometrische Interpretation ist es im Großen und Ganzen egal, welche "Version" des Vektors man verwendet. Man kann sich hierbei also einfach die bequemere Schreibweise aussuchen. Bei der Durchführung von Rechenoperationen ist die Entscheidung schon wichtiger. Dazu werden wir weiter unten kommen.

Aus der Definition eines n-Tupels leiten sich zwei Dinge ab:

1. n gibt an, aus wie vielen Komponenten der Vektor besteht.
2. Die Reihenfolge der Komponenten ist wichtig. Die Vertauschung von Komponenten erzeugt einen anderen Vektor!

Für die Anschauung sind 2- und 3-komponentige Vektoren, also Vektoren in der Ebene und im Raum, praktisch. In der Mathematik, in der man sich ja (bekanntermaßen) an fehlender Anschauung nicht sehr stört, kann man problemlos auch mit n-komponentigen Vektoren arbeiten. Das Schöne dabei ist, dass sich an den Grundprinzipien nichts ändert. Im nächsten Abschnitt wird es dazu ein Beispiel geben.


Geometrisch: Der Pfeil, durch den der Vektor symbolisiert wird, zeichnet sich durch drei Angaben aus, die in gleicher Weise für den Vektor von Bedeutung sind: seine Länge, seine Richtung und seine Orientierung, wobei Orientierung meint, an welcher Seite des Pfeils die Pfeilspitze ist.
Damit ist schon ganz schön viel über einen Vektor festgelegt. Wichtig ist aber auch, was nicht festgelegt ist: Auch wenn Anfangs- und Endpunkt eines Vektors durchaus eine Rolle spielen können, sind sie im Allgemeinen unerheblich. Das heißt: Der Begriff "Vektor" bezeichnet nicht einen Pfeil, sondern viele, nämlich all diejenigen, die die gleiche Länge, gleiche Richtung und gleiche Orientierung haben. Falls Ihnen das komisch vorkommt: Letztendlich ist es bei Brüchen ganz ähnlich: $\frac{1} {2}$ und $\frac{2} {4}$ sehen zwar unterschiedlich aus, meinen aber die gleiche Zahl.
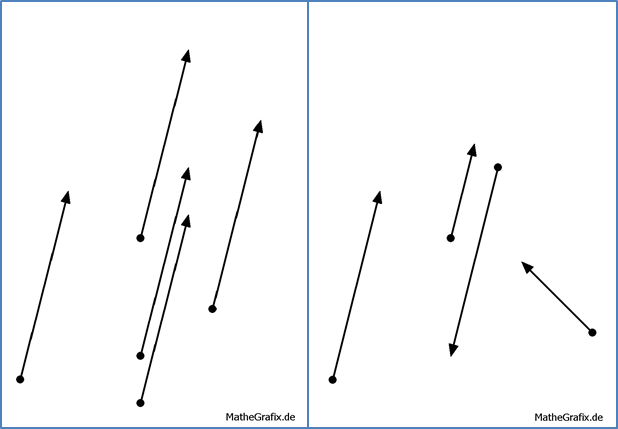
Auf der linken Seite der folgenden Grafik sehen Sie fünf Pfeile, die alle die gleiche Länge, die gleiche Richtung und die gleiche Orientierung haben. Es ist also ein Vektor dargestellt. Anfangs- und Endpunkt spielen dabei keine Rolle. Die Pfeile auf der rechten Seite unterscheiden sich hinsichtlich Länge, Richtung und/oder Orientierung. Hier sind also vier verschiedene Vektoren symbolisiert.

Um von der Komponenten- zur grafischen Darstellung zu kommen und umgekehrt, braucht man - wie schon an anderen Stellen - ein Koordinatensystem. Das 2-achsige Koordinatensystem, welches wir bislang für Funktionen verwendet haben, hilft allerdings nur weiter, wenn die Vektoren zwei Komponenten haben. Haben die Vektoren drei Komponenten, benötigt man entsprechend ein Koordinatensystem mit drei Achsen. Mit Vektoren mit mehr als drei Komponenten lässt sich zwar problemlos rechnen. Da es mit der Anschauung dann aber sowieso nicht mehr funktioniert, brauchen wir uns auch keine Gedanken über ein passendes Koordinatensystem zu machen ...
Wie funktioniert das nun konkret: Betrachten wir zwei Punkte (der Einfachheit halber in der Ebene, sodass wir 2-komponentige Vektoren bekommen) $P\left(x_p\mid y_p\right)$ und $Q\left(x_q\mid y_q\right)$. Möchte man von $P$ zu $Q$ gelangen, muss man sich $x_q-x_p$ Einheiten in x-Richtung und $y_q-y_p$ Einheiten in y-Richtung bewegen. Damit haben wir auch schon den entsprechenden Vektor berechnet. Man erhält also einen Vektor aus seinem Anfangs- und Endpunkt, indem man die Koordinaten des Anfangspunkts von den Koordinaten des Endpunkts subtrahiert. Man schreibt dafür $\vec{PQ}=\begin{pmatrix}x_q\cr y_q\end{pmatrix}-\begin{pmatrix}x_p\cr y_p\end{pmatrix}=\begin{pmatrix}x_q-x_p\cr y_q-y_p\end{pmatrix}=\begin{pmatrix}x\cr y\end{pmatrix}$
Dieser Vektor $\vec{PQ}$ trägt zwar noch die Punkte im Namen, sagt aber letztendlich nur aus, dass man $x$ Schritte in x-Richtung und $y$ Schritte in y-Richtung gegangen ist. Damit haben wir den Kreis geschlossen zu der Aussage, dass ein Vektor nicht einen, sondern viele Pfeile bezeichnet. Dass diese Pfeile alle die gleiche Länge, gleiche Richtung und gleiche Orientierung haben, ist nicht so überraschend, weil sie ja alle aus den Komponenten $x$ und $y$ bestehen.
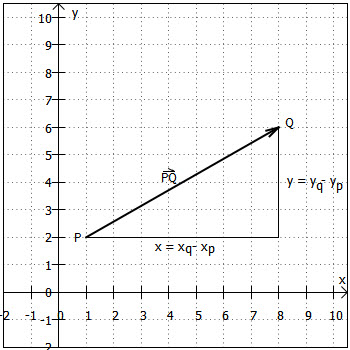
Ein Beispiel: Die Grafik rechts zeigt, wie aus den Punkten $P\left(1\mid 2\right)$ und $Q\left(8\mid 6\right)$ der Vektor $\vec{PQ}$ berechnet wird: $\vec{PQ}=\begin{pmatrix}8\cr6\end{pmatrix}-\begin{pmatrix}1\cr2\end{pmatrix}=\begin{pmatrix}8-1\cr6-2\end{pmatrix}=\begin{pmatrix}7\cr4\end{pmatrix}$


Eine Folgerung: Zwei Vektoren $\vec{a}$ und $\vec{b}$ sind dann gleich, wenn sie die gleiche Anzahl Zeilen bzw. Spalten haben und alle Komponenten gleich sind. Man schreibt in diesem Fall: $\vec{a}=\vec{b}$ bzw. $\begin{pmatrix}a_1\cr a_2\cr a_3\end{pmatrix}=\begin{pmatrix}b_1\cr b_2\cr b_3\end{pmatrix}$
Umgekehrt bedeutet das, dass zwei Vektoren dann verschieden sind, wenn sie sich in mindestens einer Komponente unterscheiden. Es müssen nicht alle Komponenten unterschiedlich sein; eine reicht völlig. Stellen Sie sich das geometrisch vor: Bereits die Veränderung einer Komponente reicht, damit die Richtung und/oder Länge des Vektors anders ist.


Noch etwas Formales: Es gibt verschiedene Varianten, wie man Vektoren bezeichnet. In diesem Kapitel werden kleine Pfeile über der (lateinischen) Variablenbezeichnung oder Pfeile über dem Anfangs- und Endpunkt des Vektors verwendet. In anderen Texten werden auch halbfette Buchstaben (was handschriftlich eher unpraktisch ist) oder Unterstriche zur Kennzeichnung verwendet. In alten Mathebüchern findet man auch altdeutsche Frakturbuchstaben als Bezeichnung. Es kommt - mathematisch gesehen - nicht darauf an. Hauptsache, die Bezeichnungen sind eindeutig und einheitlich.

 

Erste Rechenoperationen mit Vektoren

Wie bei vielen mathematischen Größen möchte man auch bei Vektoren wissen, wie man mit ihnen rechnet - sonst würde man ja nicht viel mit ihnen anfangen können ...

Eine Einschränkung zu Beginn: Nicht alle diese Rechenoperationen sind in allen Anwendungszusammenhängen wirklich sinnvoll und aussagekräftig. Sie zu definieren ist natürlich trotzdem wichtig, um an den richtigen Stellen richtig mit ihnen umgehen zu können. Auch bei Skalaren führt ja nicht jede Rechnung automatisch zu einer brauchbaren Aussage. Beispiel: Die Feststellung, dass alle Professorinnen und Professoren einer Hochschule zusammen $5.884$ Jahre alt sind, lässt sich nicht sinnvoll interpretieren. Die Aussage, dass das durchschnittliche Alter der Professorinnen und Professoren $61{,}2$ Jahre ist, ist hingegen für die Personalplanung eine wichtige Größe.

Ebenso muss man auf die Einheiten aufpassen - und auch hier ist es bei Skalaren genauso: $5=5$ ist sicher richtig. $5\, m=5\, kg$ passt weder von den Einheiten zusammen noch lassen sich sinnvolle Aussagen daraus ableiten.


Hier nun das oben versprochene Beispiel:
Der Zeilenvektor $\vec{k}^{\,T}=\begin{pmatrix}0{,}5;\, 0{,}125;\, 3;\, 0{,}2;\, 0{,}2;\, 1\end{pmatrix}$ bezeichne das Rezept eines Rührkuchens: $0{,}5\,kg$ Mehl, $0{,}125\,l$ Milch, $3$ Eier, $0{,}2\,kg$ Butter, $0{,}2\,kg$ Zucker und $1$ Päckchen Backpulver. Auch wenn man Kuchenrezepte in Realität natürlich nicht als Vektor abbildet, lassen sich an diesem Beispiel einige Dinge gut veranschaulichen:

1. Wir haben damit (ohne große Probleme) einen 6-komponentigen Vektor erzeugt. Wie oben gesagt: Ein Vektor ist erstmal "nur" eine Zusammenstellung von Werten. Man kann den Vektor $\vec{k}^{\,T}$ zwar nicht zeichnen, verstehen kann man ihn trotzdem.
2. Die Einheiten sind in diesem Vektor genauso wichtig wie sonst: Ändert man den Vektor zu $\vec{k_1}^{T}=\begin{pmatrix}500;\, 0{,}125;\, 3;\, 0{,}2;\, 0{,}2;\, 1\end{pmatrix}$, sollte man dazu sagen, dass die Mehlmenge jetzt in Gramm angegeben ist. Mit $500\,kg$ Mehl wird der Kuchen sicher nichts ...
3. Auch das Vertauschen von Komponenten geht nicht einfach so: Den Vektor $\vec{k_2}^{T}=\begin{pmatrix}1;\, 0{,}125;\, 3;\, 0{,}2;\, 0{,}2;\, 500\end{pmatrix}$ muss man in diesem Zusammenhang interpretieren als: $1\,g$ Mehl, $0{,}125\,l$ Milch, $3$ Eier, $0{,}2\,kg$ Butter, $0{,}2\,kg$ Zucker und $500$ Päckchen Backpulver. Ich denke, das spricht für sich ...

 

Addition und Subtraktion

Voraussetzung dafür, dass Vektoren addiert werden können, ist, dass alle Vektoren gleich viele Komponenten haben. Gleiches gilt (natürlich) für die Subtraktion. In den Formeln dieses Kapitels werden bloß Vektoren mit $3$ Komponenten betrachtet. Für Vektoren mit $2$, $4$ oder mehr Komponenten funktionieren die Konzepte genauso. Damit die Vektoren ordentlich gezeichnet werden können, wurden für die Beispiele 2-komponentige Vektoren gewählt.

 

Addition

Komponentenweise: Die Summe zweier Vektoren $\vec{a}$ und $\vec{b}$ berechnet man, indem man die Komponenten der beiden Vektoren zeilenweise addiert, also $\vec{a}+\vec{b}=\begin{pmatrix}a_1\cr a_2\cr a_3\end{pmatrix}+\begin{pmatrix}b_1\cr b_2\cr b_3\end{pmatrix}=\begin{pmatrix}a_1+b_1\cr a_2+b_2\cr a_3+b_3\end{pmatrix}$

Geometrisch: Geometrisch verschiebt man bei der Addition von zwei Vektoren $\vec{a}$ und $\vec{b}$ den zweiten Vektor $\vec{b}$ parallel, sodass sein Anfangspunkt im Endpunkt von $\vec{a}$ liegt. Der Summenvektor führt dann vom Anfangspunkt von $\vec{a}$ zum Endpunkt von $\vec{b}$. In der Schreibweise mit Anfangs- und Endpunkt ergibt sich daraus die folgende Gleichung: $\vec{AB}+\vec{BC}=\vec{AC}$. Da das entstehende Dreieck zu einem Parallelogramm ergänzt werden kann, kann man auch sagen: Der Summenvektor ist die Diagonale des Parallelogramms, das aus den Vektoren gebildet wird.

Beispiel: Gegeben seien $\vec{a}=\begin{pmatrix}4\cr-8\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}2\cr3\end{pmatrix}$. Dann ist $\vec{a}+\vec{b}=\begin{pmatrix}4\cr-8\end{pmatrix}+\begin{pmatrix}2\cr3\end{pmatrix}=\begin{pmatrix}4+2\cr-8+3\end{pmatrix}=\begin{pmatrix}6\cr-5\end{pmatrix}$

Hier die zugehörige Grafik:

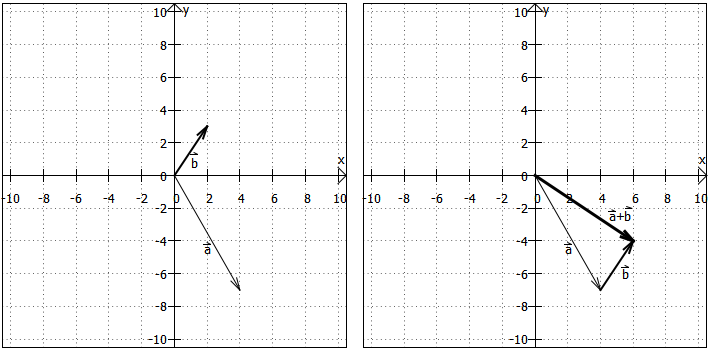
Bei der Addition von mehr als zwei Vektoren erweitert man dieses Verfahren einfach, also: Anfangspunkt des zweiten Vektors an Endpunkt des ersten, Anfangspunkt des dritten Vektors an Endpunkt des zweiten, Anfangspunkt des vierten Vektors an Endpunkt des dritten, ... und verbindet den Anfangspunkt des ersten Vektors mit den Endpunkt des letzten - fertig. Dabei kann es passieren, dass der Endpunkt des letzten Vektors genau auf dem Anfangspunkt des ersten Vektors liegt. Die Summe aller dieser Vektoren ist dann $\vec{0}$. Dass man in Formelschreibweise einfach die entsprechenden Komponenten der einzelnen Vektoren - egal wie viele es sind - addiert, versteht sich fast von selbst ...


Zwei ganz wichtige Vektoren in diesem Zusammenhang:

• Der Nullvektor: $\vec{0}=\begin{pmatrix}0\cr0\cr0\end{pmatrix}$. Geometrisch gesehen, bildet der Nullvektor einen Punkt auf sich selbst ab und ist daher der einzige Vektor, für den die Veranschaulichung durch einen Pfeil nicht funktioniert. Bitte achten Sie darauf, dass $0$ (ein Skalar) und $\vec{0}$ (ein Vektor, bestehend aus mehreren Werten) zwei völlig unterschiedliche Gebilde sind.
  
  
• Der Gegenvektor: Zu einem Vektor $\vec{a}=\begin{pmatrix}a_1\cr a_2\cr a_3\end{pmatrix}$ ist $-\vec{a}=\begin{pmatrix}-a_1\cr-a_2\cr-a_3\end{pmatrix}$ der sogenannte Gegenvektor. Geometrisch betrachtet, hat $-\vec{a}$ die gleiche Länge und die gleiche Richtung wie $\vec{a}$, aber die entgegengesetzte Orientierung. Anders gesagt, wenn $\vec{a}$ von Punkt $A$ zu Punkt $B$ verläuft, verläuft $-\vec{a}$ von $B$ zu $A$.

 

Subtraktion

Wie beim "normalen Rechnen" ist auch bei Vektoren die Subtraktion die Umkehrung der Addition. Das macht die Sache einfach:

Komponentenweise: Die Differenz zweier Vektoren berechnet man, indem man die Komponenten der beiden Vektoren zeilenweise subtrahiert, also $\vec{a}-\vec{b}=\begin{pmatrix}a_1\cr a_2\cr a_3\end{pmatrix}-\begin{pmatrix}b_1\cr b_2\cr b_3\end{pmatrix}=\begin{pmatrix}a_1-b_1\cr a_2-b_2\cr a_3-b_3\end{pmatrix}$
Wenn man möchte, kann man das - ähnlich wie bei ganzen Zahlen - als Addition des Gegenvektors verstehen: $\vec{a}-\vec{b}=\vec{a}+\left(-\vec{b}\right)=\begin{pmatrix}a_1\cr a_2\cr a_3\end{pmatrix}+\begin{pmatrix}-b_1\cr-b_2\cr-b_3\end{pmatrix}=\begin{pmatrix}a_1-b_1\cr a_2-b_2\cr a_3-b_3\end{pmatrix}$. Das Ergebnis ist natürlich dasselbe.

Geometrisch: Der Gedanke mit dem Gegenvektor liefert einen guten Einstieg für die geometrische Variante von $\vec{a}-\vec{b}$: Da $\vec{a}-\vec{b}=\vec{a}+\left(-\vec{b}\right)$, verschiebt man den Gegenvektor von $\vec{b}$ so, dass sein Anfangspunkt im Endpunkt von $\vec{a}$ liegt. Der Differenzvektor führt dann vom Anfangspunkt von $\vec{a}$ zum Endpunkt von $-\vec{b}$. Alternativ kann man sich die Frage stellen, welcher Vektor zu $\vec{b}$ addiert werden muss, damit $\vec{a}$ herauskommt - auch diese Überlegung kennt man vom Rechnen mit Skalaren.

Beispiel: Gegeben seien wieder $\vec{a}=\begin{pmatrix}4\cr-5\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}2\cr3\end{pmatrix}$. Dann ist $\vec{a}-\vec{b}=\begin{pmatrix}4\cr-5\end{pmatrix}-\begin{pmatrix}2\cr3\end{pmatrix}=\begin{pmatrix}4-2\cr-5-3\end{pmatrix}=\begin{pmatrix}2\cr-8\end{pmatrix}$

Hier die zugehörige Grafik:

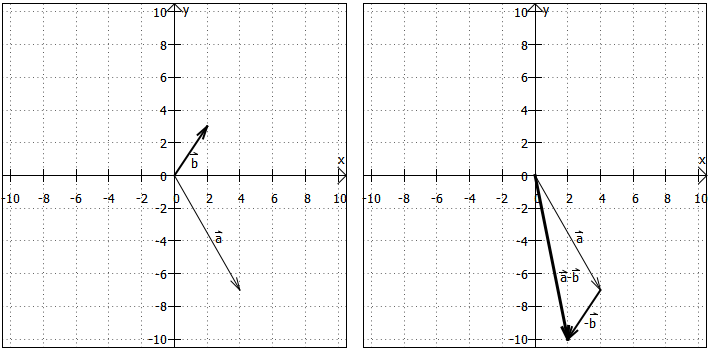
Da sich Addition und Subtraktion von Vektoren direkt auf die Addition und Subtraktion von reellen Zahlen zurückführen lassen, gelten hier die gleichen Rechengesetze, z. B. Kommutativ- und Assoziativgesetz. Das heißt, Vektoren verhalten sich hier angenehmerweise so, wie man es gewohnt ist.

 

Skalare Multiplikation

Eine Bemerkung vorweg: Aus Gründen, die wahrscheinlich keine/r mehr wirklich benennen kann, bezeichnet man Skalare in der Vektorrechnung gerne mit griechischen Buchstaben, am liebsten mit $\lambda$ (gesprochen: "lambda") oder $\mu$ (gesprochen: "mü"). Geschickt ist das auf jeden Fall, weil dadurch Verwechslungen zwischen Skalaren und Vektoren vermieden werden.


Komponentenweise: Ein Vektor $\vec{a}$ wird mit dem Skalar $\lambda\in\mathbb{R}$ multipliziert, indem jede Komponente des Vektors mit dem Skalar multipliziert wird, also $\lambda\cdot \vec{a}=\lambda\cdot\begin{pmatrix}a_1\cr a_2\cr a_3\end{pmatrix}=\begin{pmatrix}\lambda\cdot a_1\cr\lambda\cdot a_2\cr\lambda\cdot a_3\end{pmatrix}$

Bemerkung 1: Den Multiplikationspunkt $\cdot$ darf man - wie bei der "normalen" Multiplikation - weglassen, wenn die Schreibweise eindeutig bleibt.
Bemerkung 2: Ebenfalls wie bei der "normalen" Multiplikation kann man die skalare Multiplikation dafür nutzen, "unhandliche" Faktoren vorzuziehen. Ein Beispiel: $\begin{pmatrix}-\frac{5}{2}\cr2\cr\frac{7}{2}\end{pmatrix}=\dfrac{1}{2}\begin{pmatrix}-5\cr4\cr7\end{pmatrix}$

Geometrisch: Die geometrische Interpretation der skalaren Multiplikation eines Vektors $\vec{a}$ mit dem Skalar $\lambda\in\mathbb{R}$ ist nicht sehr überraschend: Die Länge des Vektors ändert sich um den Faktor $\left|\lambda\right|$ . An der Richtung ändert sich hingegen nichts. Eventuell wird allerdings die Orientierung umgekehrt. Das charakterisiert man mit folgenden Begriffen:

• Multipliziert man einen Vektor $\vec{a}$ mit einem positiven Skalar $\lambda_1$, so hat $\lambda_1\vec{a}$ die gleiche Orientierung wie $\vec{a}$. Die Vektoren $\vec{a}$ und $\lambda_1\vec{a}$ sind parallel oder auch gleichsinnig parallel.
  
  
• Multipliziert man einen Vektor $\vec{a}$ mit einem negativen Skalar $\lambda_2$, so hat $\lambda_2\vec{a}$ die entgegen gesetzte Orientierung von $\vec{a}$. Die Vektoren $\vec{a}$ und $\lambda_2\vec{a}$ sind antiparallel oder auch gegensinnig parallel. Die Multiplikation mit $-1$ erzeugt den Gegenvektor.
  
  
• Multipliziert man einen Vektor mit $0$, entsteht der Nullvektor, was vermutlich wenig überraschen wird ... Anders ist es da schon mit der Festlegung, dass der Nullvektor zu jedem Vektor parallel ist. Dies ist nicht wirklich offensichtlich, aber später in verschiedenen Zusammenhängen nützlich.

Parallele und antiparallele Vektoren lassen sich durch Parallelverschiebung in eine Linie bringen. Sie heißen deshalb auch kollinear (abgeleitet vom Lateinischen "collinearis": auf der gleichen Gerade/Linie liegend).

Bis hierhin wurden in diesem Kapitel bloß Vektoren mit $3$ Komponenten betrachtet. Für Vektoren mit $2$, $4$ oder mehr Komponenten funktionieren die Konzepte genauso. Auch hier noch zwei Beispiele mit einem 2-komponentigen Vektor:

• Parallelität: Gegeben seien $\vec{a}=\begin{pmatrix}3\cr-4\end{pmatrix}$ und $\lambda_1 =2$ . Das skalare Produkt ist $\lambda_1\vec{a}=2\begin{pmatrix}3\cr-4\end{pmatrix}=\begin{pmatrix}2\cdot 3\cr2\cdot \left(-4\right)\end{pmatrix}=\begin{pmatrix}6\cr-8\end{pmatrix}$
  
  
• Antiparallelität: Gegeben seien $\vec{a}=\begin{pmatrix}3\cr-4\end{pmatrix}$ und $\lambda_2=-2{,}5$ . Das skalare Produkt ist $\lambda_2\vec{a}=-2{,}5\begin{pmatrix}3\cr-4\end{pmatrix}=\begin{pmatrix}-2{,}5\cdot 3\cr-2{,}5\cdot \left(-4\right)\end{pmatrix}=\begin{pmatrix}-7{,}5\cr10\end{pmatrix}$

Hier das Ganze in einer Grafik:

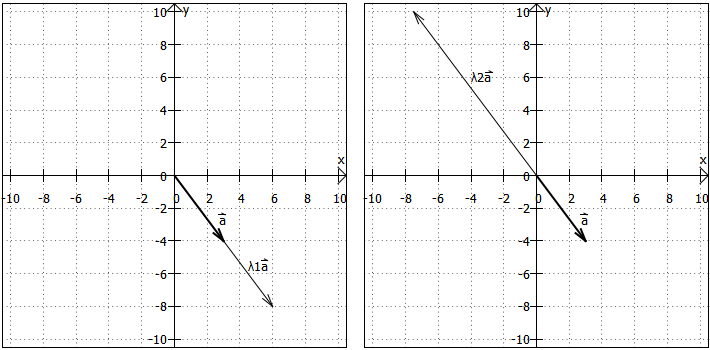
Aus dem gleichen Grund wie bei Addition und Subtraktion gelten auch hier das Kommutativ- und das Assoziativgesetz sowie zusätzlich zwei Varianten des Distributivgesetzes: Für die Vektoren $\vec{a}$ und $\vec{b}$ sowie die Skalare $\lambda , \mu\in\mathbb{R}$ gelten

• $\lambda\left(\vec{a}+\vec{b}\right)=\lambda\vec{a}+\lambda\vec{b}$
• $\left(\lambda+\mu\right)\vec{a}=\lambda\vec{a}+\mu\vec{a}$

 

Was ist eine Linearkombination?

Mit diesen gerade besprochenen Rechenoperationen kann man schon eine ganze Menge erreichen: Bereits mit zwei 2-komponentigen Vektoren kann man mithilfe von Vektoraddition und skalarer Multiplikation eine komplette Ebene erzeugen. Drei 3-komponentige Vektoren und Vektoraddition und skalare Multiplikation reichen für den 3-dimensionalen Raum.

Etwas formaler die folgende Vokabel:
Definition: Verknüpft man mehrere n-komponentige Vektoren mittels Addition und skalarer Multiplikation, spricht man von einer Linearkombination. In einer Formel: $\vec{a}=\lambda_1\vec{a_1}+\lambda_2\vec{a_2}+\dots+\lambda_n\vec{a_n}$ mit den Skalaren $\lambda_1,\dots, \lambda_n\in\mathbb{R}$ und den n-komponentigen Vektoren $\vec{a_1}$ bis $\vec{a_n}$.
Wichtig: Eine Linearkombination von Vektoren ergibt wieder einen Vektor. In diesem Fall ist das der Vektor $\vec{a}$.

Ein Beispiel:
Wir betrachten noch mal das Kuchenbeispiel von oben. Ein Rezept für Nusskuchen lautet: $0{,}4\,kg$ Mehl, $0{,}125\,l$ Milch, $4$ Eier, $0{,}15\,kg$ Butter, $0{,}2\,kg$ Zucker, $1{,}5$ Päckchen Backpulver und $0{,}3\,kg$ Nüsse. Dieses Rezept lässt sich durch den Vektor $\vec{k_N}^{T}=\begin{pmatrix}0{,}4;\, 0{,}125;\, 4;\, 0{,}15;\, 0{,}2;\, 1{,}5;\, 0{,}3\end{pmatrix}$ darstellen.
Damit der Vektor $\vec{k}^{\,T}$ des Rührkuchens die gleiche Anzahl an Komponenten hat, müssen wir als letzte Komponente eine $0$ ergänzen, denn Nüsse sind ja nicht enthalten: $\vec{k_R}^{T}=\begin{pmatrix}0{,}5;\, 0{,}125;\, 3;\, 0{,}2;\, 0{,}2;\, 1;\, 0\end{pmatrix}$ . Bitte beachten Sie, dass der Rührkuchenvektor einen anderen Namen bekommen hat! Da nur Vektoren, die die gleiche Anzahl von Komponenten haben, identisch sein können, gilt: $\vec{k_R}^{T}\neq\vec{k}^{\,T}$

Nun lässt sich mithilfe einer Linearkombination bestimmen, wie viele Zutaten vorhanden sein müssen, wenn $3$ Nusskuchen und $2$ Rührkuchen gebacken werden sollen, nämlich:
$\begin{array}{rcl}\vec{z} &=& 3\cdot\vec{k_N}^{T} + 2\cdot\vec{k_R}^{T} \cr\cr &=& 3\cdot\begin{pmatrix}0{,}4;\, 0{,}125;\, 4;\, 0{,}15;\, 0{,}2;\, 1{,}5;\, 0{,}3\end{pmatrix} + 2\cdot \begin{pmatrix}0{,}5;\, 0{,}125;\, 3;\, 0{,}2;\, 0{,}2;\, 1;\, 0\end{pmatrix} \cr \cr &=& \begin{pmatrix}3\cdot 0{,}4;\, 3\cdot 0{,}125;\, 3\cdot 4;\, 3\cdot 0{,}15;\, 3\cdot 0{,}2;\, 3\cdot 1{,}5;\, 3\cdot 0{,}3\end{pmatrix} + \begin{pmatrix}2\cdot 0{,}5;\, 2\cdot 0{,}125;\, 2\cdot 3;\, 2\cdot 0{,}2;\, 2\cdot 0{,}2;\, 2\cdot 1;\, 2\cdot 0\end{pmatrix} \cr \cr &=& \begin{pmatrix}1{,}2;\, 0{,}375;\, 12;\, 0{,}45;\, 0{,}6;\, 4{,}5;\, 0{,}9\end{pmatrix} + \begin{pmatrix}1;\, 0{,}25;\, 6;\, 0{,}4;\, 0{,}4;\, 2;\, 0\end{pmatrix} \cr \cr &=& \begin{pmatrix}1{,}2+1;\, 0{,}375+0{,}25;\, 12+6;\, 0{,}45+0{,}4;\, 0{,}6+0{,}4;\, 4{,}5+2;\, 0{,}9+0 \end{pmatrix} \cr \cr &=& \begin{pmatrix}2{,}2;\, 0{,}625;\, 18;\, 0{,}85;\, 1;\, 6{,}5;\, 0{,}9\end{pmatrix} \end{array}$
Man benötigt also insgesamt $2{,}2\,kg$ Mehl, $0{,}625\,l$ Milch, $18$ Eier, $0{,}85\,kg$ Butter, $1\,kg$ Zucker, $6{,}5$ Päckchen Backpulver und $0{,}9\,kg$ Nüsse.

Zugegebenermaßen hätte man das auch ohne Vektorrechnung problemlos ausrechnen können. Das Beispiel soll auch nur zeigen, dass sich hinter dem Begriff "Linearkombination" kein wirklich schwieriges Konzept versteckt ...

 

Der Betrag eines Vektors

Definition: Der Betrag eines Vektors $\vec{a}$ ist ein Maß für seine Länge oder - wenn man es anschaulich möchte - ein Maß für die Länge des Pfeils. Wie bei Zahlen schreibt man dafür: $\left|\vec{a}\right|$.


Komponentenweise:
Bei der Berechnung hilft uns ein "alter Bekannter", nämlich der Satz des Pythagoras. Daraus ergeben sich die folgenden Formeln: $\left| \vec{a} \right| = \begin{pmatrix}a_1\cr a_2\end{pmatrix} = \sqrt{{a_1}^2 + {a_2}^2}$ für 2-komponentige Vektoren, $\left| \vec{a} \right| = \begin{pmatrix}a_1\cr a_2\cr a_3\end{pmatrix} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2 }$ für 3-komponentige Vektoren bzw. $\left| \vec{a} \right| = \begin{pmatrix}a_1\cr a_2\cr\vdots\cr a_n\end{pmatrix} = \sqrt{{a_1}^2 + {a_2}^2 + \ldots + {a_n}^2 }$ für den allgemeinen Fall.
Aufgrund der Wurzeleigenschaften ist der Betrag eines Vektors natürlich immer größer oder gleich $0$. Ist ja für eine Länge auch logisch ... Weil die einzelnen Komponenten unter der Wurzel quadriert werden, gilt $\left|\vec{a}\right|=\left|-\vec{a}\right|$


Geometrisch:

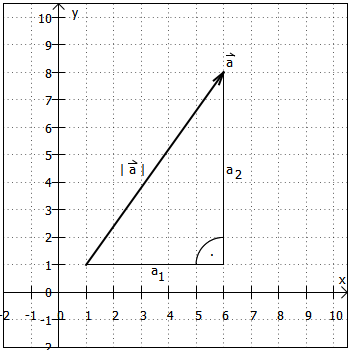
Damit haben wir gleichzeitig erklärt, wo diese Formeln herkommen - zumindest für den 2-dimensionalen Fall ...

Ein geometrischer Anwendungsfall: Um von zwei gegebenen Vektoren $\vec{a}$ und $\vec{b}$ den Abstand ihrer Endpunkte zu bestimmen, rechnet man: $\left|\vec{a}-\vec{b}\right|$ bzw. $\left|\vec{b}-\vec{a}\right|$ . Da sich $\vec{a}-\vec{b}$ und $\vec{b}-\vec{a}$ nur im Vorzeichen unterscheiden, das ja durch den Betrag ohnehin wegfällt, ist es egal, welche Differenz man bildet.


Und nun ein Beispiel:
Gegeben sei $\vec{a} = \begin{pmatrix}9\cr-10\cr1\end{pmatrix}$
Der Betrag dieses Vektors ist $\left|\vec{a}\right|=\sqrt{9^2+\left(-10\right)^2+1^2}=\sqrt{182}\approx 13{,}49$


Statt vom "Betrag des Vektors" wird auch von der "Norm des Vektors" gesprochen. Statt $\left|\vec{a}\right|$ schreibt man dann $\Vert\vec{a}\Vert$ . Das Konzept der "Norm" ist in der höheren Mathematik von größerer Bedeutung, als hier vielleicht deutlich wird. Schon mal gut zu wissen ist, dass normierte Vektoren, sprich Vektoren, die den Betrag $1$ haben, häufig nützlich sind. Um einen beliebigen Vektor $\vec{a}\neq\vec{0}$ zu normieren, muss man diesen Vektor mit dem Kehrwert seines Betrages skalarmultiplizieren, man rechnet also: $\vec{a_n} = \dfrac{1}{\left|\vec{a}\right|}\,\vec{a}$. Der entstehende Vektor hat dieselbe Richtung und Orientierung wie $\vec{a}$, aber eben den Betrag $1$. Im oberen Beispiel würde das so aussehen: $\vec{a_n} = \dfrac{1}{\sqrt{182}}\begin{pmatrix}9\cr-10\cr1\end{pmatrix}$

 

Lineare Unabhängigkeit

Ein wichtiges Konzept bei Vektoren, das es so bei Zahlen nicht gibt, ist die lineare Unabhängigkeit.

Definition: Die Vektoren $\vec{a_1} , \vec{a_2} , \dots , \vec{a_n}$ heißen linear unabhängig, wenn die Gleichung $\lambda_1\vec{a_1}+\lambda_2\vec{a_2}+\dots+\lambda_n\vec{a_n}=\vec{0}$ nur die Lösung $\lambda_1=\lambda_2=\dots\lambda_n=0$ hat.
Anders gesagt: Eine Linearkombination dieser Vektoren ergibt nur dann den Nullvektor, wenn alle skalaren Koeffizienten $0$ sind.
Und noch eine andere Formulierung: Keiner der Vektoren lässt sich aus den anderen kombinieren.

Definition: Die Vektoren $\vec{a_1} , \vec{a_2} , \dots , \vec{a_n}$ heißen linear abhängig, wenn die Gleichung $\lambda_1\vec{a_1}+\lambda_2\vec{a_2}+\dots+\lambda_n\vec{a_n}=\vec{0}$ mehrdeutig lösbar ist. Das heißt, wenn die Gleichung nicht nur die Lösung $\lambda_1=\lambda_2=\dots\lambda_n=0$ hat, sondern es noch weitere Lösungen gibt.
Anders gesagt: Eine Linearkombination dieser Vektoren ergibt auch dann den Nullvektor, wenn nicht alle skalaren Koeffizienten $0$ sind.
Und auch hier noch eine andere Formulierung: Mindestens einer dieser Vektoren ist eine Linearkombination der übrigen Vektoren, lässt sich also mithilfe der anderen darstellen.


Ein Merksatz zur linearen Unabhängigkeit:
Die Anzahl der Komponenten gibt vor, wie viele linear unabhängige Vektoren es maximal geben kann: in der Ebene zwei, im Raum drei. Die Vektoren $\begin{pmatrix}1\cr0\cr0\end{pmatrix}$, $\begin{pmatrix}0\cr1\cr0\end{pmatrix}$ und $\begin{pmatrix}0\cr0\cr1\end{pmatrix}$ (Man nennt sie auch Einheitsvektoren.) sind das beste Beispiel dafür: Es gibt keine weitere Möglichkeit, eine $1$ in einen 3-komponentigen Vektor "unterzubringen".
Wichtige Folgerung: Jeder weitere Vektor mit $3$ Komponenten lässt sich eindeutig aus diesen erzeugen. Das ist natürlich nicht bloß bei diesen speziellen Vektoren so: Hat man drei linear unabhängige 3-komponentige Vektoren, kann man damit jeden Vektor des 3-dimensionalen Raumes eindeutig darstellen.


Merksätze zur linearen Abhängigkeit:

• Eine Menge von Vektoren, die den Nullvektor enthält, ist immer linear abhängig. Zur Verdeutlichung ein Beispiel: Die Vektorgleichung $\lambda_1\begin{pmatrix}1\cr0\cr-4\end{pmatrix}+\lambda_2\begin{pmatrix}-3\cr-2\cr7\end{pmatrix}+\lambda_3\begin{pmatrix}0\cr0\cr0\end{pmatrix}=\vec{0}$ hat unendlich viele Lösungen, z. B.
  • $\lambda_1 =0$ , $\lambda_2 =0$ und $\lambda_3 =1$
  • $\lambda_1 =0$ , $\lambda_2 =0$ und $\lambda_3=-5$
  • $\lambda_1 =0$ , $\lambda_2 =0$ und $\lambda_3=\frac{112}{47}$
  • oder oder oder ...
    
    
• Eine Menge linear abhängiger Vektoren enthält sozusagen "überflüssige" Informationen: Betrachtet man zwei linear abhängige Vektoren, beispielsweise $\vec{a}$ und $2\vec{a}$, kann man mit ihnen sämtliche Punkte einer Geraden darstellen. Das hätte man aber auch mit nur einem der beiden Vektoren erreichen können. Zwei linear unabhängige Vektoren spannen hingegen eine Ebene auf. Man "gewinnt" also eine Dimension hinzu. Das führt zu den folgenden beiden Aussagen:
  • Zwei Vektoren sind linear abhängig, wenn sie parallel sind.
  • Drei Vektoren sind linear abhängig, wenn sie in einer Ebene liegen. So, wie zwei parallele Vektoren kollinear heißen (siehe oben), heißen drei Vektoren, die in einer Ebene liegen, komplanar (abgeleitet vom Lateinischen "planum": in der gleichen Ebene/Plane liegend).

Wie stellt man nun fest, ob eine Menge von Vektoren linear (un)abhängig ist?
Es ist leider so, dass es Vektoren meist nicht sofort anzusehen ist, ob sie linear abhängig oder linear unabhängig sind. Daher folgendes Verfahren: Man betrachtet $\lambda_1\vec{a_1}+\lambda_2\vec{a_2}+\dots+\lambda_n\vec{a_n}=\vec{0}$, also eine Vektorgleichung mit den Variablen $\lambda_1$ bis $\lambda_n$. Daraus entsteht ein lineares Gleichungssystem, dessen Lösung Auskunft über die lineare (Un)Abhängigkeit der Vektoren gibt.

Hier der Rechenweg anhand von zwei Beispielen:
1.
Gegeben seien die drei Vektoren $\begin{pmatrix}1\cr-1\cr1\end{pmatrix}$ , $\begin{pmatrix}3\cr0\cr4\end{pmatrix}$ und $\begin{pmatrix}11\cr-5\cr3\end{pmatrix}$
Um zu entscheiden, ob sie linear abhängig oder unabhängig sind, muss die folgende Gleichung gelöst werden: $\lambda_1\begin{pmatrix}1\cr-1\cr1\end{pmatrix}+\lambda_2\begin{pmatrix}3\cr0\cr4\end{pmatrix}+\lambda_3\begin{pmatrix}11\cr-5\cr3\end{pmatrix}=\vec{0}$

Diese führt zu dem Gleichungssystem:
$\begin{array}{crcrcrcrl} \text{I} & \lambda_1 &+& 3\lambda_2 &+& 11\lambda_3 &=& 0 \cr \text{II} & -\lambda_1 & & &-& 5\lambda_3 &=& 0 \cr \text{III} & \lambda_1 &+& 4\lambda_2 &+& 3\lambda_3 &=& 0 \cr \cr \text{I} & \lambda_1 &+& 3\lambda_2 &+& 11\lambda_3 &=& 0 \cr \text{I+II} & & & 3\lambda_2 &+& 6\lambda_3 &=& 0 \cr \text{I-III} & & & -\lambda_2 &+& 8\lambda_3 &=& 0 \cr \cr \text{I} & \lambda_1 &+& 3\lambda_2 &+& 11\lambda_3 &=& 0 \cr \text{II'} & & & 3\lambda_2 &+&6\lambda_3 &=& 0 \cr \text{II'+3 III'} & & & & & 30\lambda_3 &=& 0 & \Rightarrow \lambda_3 = 0 \cr \cr \text{II'} & & & 3\lambda_2 &+& 6\cdot 0 &=& 0 & \Rightarrow \lambda_2 = 0 \cr \text{I} & \lambda_1 &+& 3 \cdot 0 &+& 11 \cdot 0 &=& 0 & \Rightarrow \lambda_1 = 0 \end{array}$

Ergebnis: Da $\lambda_1=\lambda_2=\lambda_3=0$ die einzige Lösung des Gleichungssystems ist, sind die drei Vektoren linear unabhängig.


2.
Gegeben seien die drei Vektoren $\begin{pmatrix}-2\cr-2\cr6\end{pmatrix}$ , $\begin{pmatrix}-5\cr3\cr-1\end{pmatrix}$ und $\begin{pmatrix}-7\cr1\cr5\end{pmatrix}$
Um zu entscheiden, ob sie linear abhängig oder unabhängig sind, muss die folgende Gleichung gelöst werden: $\lambda_1\begin{pmatrix}-2\cr-2\cr6\end{pmatrix}+\lambda_2\begin{pmatrix}-5\cr3\cr-1\end{pmatrix}+\lambda_3\begin{pmatrix}-7\cr1\cr5\end{pmatrix}=\vec{0}$

Diese führt zu dem Gleichungssystem:
$\begin{array}{crcrcrcr} \text{I} & -2\lambda_1 &-& 5\lambda_2 &-& 7\lambda_3 &=& 0 \cr \text{II} & -2\lambda_1 &+& 3\lambda_2 &+& \lambda_3 &=& 0 \cr \text{III} & 6\lambda_1 &-& \lambda_2 &+& 5\lambda_3 &=& 0 \cr \cr \text{I} & -2\lambda_1 &-& 5\lambda_2 &-& 7\lambda_3 &=& 0 \cr \text{I-II} & & & -8\lambda_2 &-& 8\lambda_3 &=& 0 \cr \text{3 I+III} & & & -16\lambda_2 &-& 16\lambda_3 &=& 0 \cr \cr \text{I} & -2\lambda_1 &-& 5\lambda_2 &-& 7\lambda_3 &=& 0 \cr \text{II'} & & & -8\lambda_2 &-& 8\lambda_3 &=& 0 \cr \text{2 II'-III'} & & & & & 0 &=& 0 \end{array}$

Wegen der entstandenen Nullzeile ist es offensichtlich unmöglich, eine eindeutige Lösung zu finden. Es gibt also unendlich viele Lösungen dieses Gleichungssystems. Sprich: Zu jeder Variable, die wir frei wählen, können wir die beiden anderen so berechnen, dass das Gleichungssystem gelöst wird. Nehmen wir z. B. $\lambda_3= 1$ . Eingesetzt in $-8\lambda_2 - 8\lambda_3 = 0$ führt dies zu $\lambda_2= -1$. Dies beides eingesetzt in die erste Gleichung ergibt $\lambda_1= -1$. Eine weitere Lösung (auf dem gleichen Weg berechnet) ist $\lambda_1 =4$, $\lambda_2 =4$ und $\lambda_3=-4$. Auch $\lambda_1=\lambda_2=\lambda_3=0$ ist im Übrigen eine Lösung des Gleichungssystems - aber eben nicht die einzige.

Ergebnis: Da die Gleichung keine eindeutige Lösung hat, sind die drei Vektoren linear abhängig. Ein Vektor lässt sich also als Linearkombination der anderen darstellen, z. B. ist $\begin{pmatrix}-2\cr-2\cr6\end{pmatrix} + \begin{pmatrix}-5\cr3\cr-1\end{pmatrix} = 1\cdot\begin{pmatrix}-2\cr-2\cr6\end{pmatrix} + 1\cdot\begin{pmatrix}-5\cr3\cr-1\end{pmatrix} = \begin{pmatrix}-7\cr1\cr5\end{pmatrix}$


Eine mathematische Randbemerkung: Da auf den rechten Seiten der Gleichungen jeweils eine $0$ steht (mathematisch nennt man so etwas ein homogenes lineares Gleichungssystem), gibt es hier nur zwei Möglichkeiten für die Lösung: Entweder ist das Gleichungssystem eindeutig lösbar mit der Lösung $\lambda_1=\lambda_2=\dots=\lambda_n=0$ ; dann sind die Vektoren linear unabhängig. Oder das Gleichungssystem hat unendlich viele Lösungen; dann sind die Vektoren linear abhängig.

Eine lerntechnische Randbemerkung: Falls Sie mit dem Lösen linearer Gleichungssysteme Schwierigkeiten haben, schauen Sie bitte im entsprechenden Kapitel nach. Dort sind die verschiedenen Lösungswege ausführlich erklärt - und Übungsaufgaben gibt es auch.


Ausblick: Es gibt weitere Wege, um festzustellen, ob Vektoren linear (un)abhängig sind, beispielsweise kann man dafür auch Determinanten nutzen.

 

Produkte von Vektoren

Bei der Multiplikation von Vektoren muss man ein bisschen aufpassen: Anders als bei "normalen Zahlen" unterscheidet man hier vier verschiedene Produkte! Neben der skalaren Multiplikation, die oben schon behandelt wurde ("Skalar mal Vektor gleich Vektor") gibt es noch das Skalarprodukt ("Vektor mal Vektor gleich Skalar"), das Vektorprodukt ("Vektor mal Vektor gleich Vektor") und das Spatprodukt, bei welchem Vektor- und Skalarprodukt verknüpft werden ("Vektor mal Vektor mal Vektor gleich Skalar"). Diese Vielfalt resultiert daraus, dass wir nicht mehr nur Objekte gleichen Typs miteinander multiplizieren (also "eine Zahl mal eine andere Zahl"), sondern nun verschiedene mathematische Objekte zur Hand haben, nämlich Zahlen und Vektoren, sodass sich einfach mehr Kombinationsmöglichkeiten ergeben.

Ganz wichtig: Eine Division durch Vektoren ist nicht definiert! Möglich ist allerdings, einen Vektor durch einen Skalar zu teilen - das ist eine Folgerung aus der skalaren Multiplikation, die ja die Multiplikation von Vektoren mit Brüchen nicht ausschließt.

 

Skalarprodukt

Wir beginnen mit dem Skalarprodukt. Das Zeichen für diese Rechenoperation ist $\cdot$, also der gleiche Multiplikationspunkt wie bei der skalaren Multiplikation. Da man Skalar und Vektor aber gut unterscheiden kann, ist das nicht das Problem. Ein bisschen aufpassen sollte man trotzdem ...
Man nennt das Skalarprodukt auch inneres Produkt oder Punktprodukt.

Wichtig vorab:

• Ein Skalarprodukt kann man nur berechnen, wenn beide Vektoren die gleiche Anzahl von Komponenten haben.
• Aus Gründen, die später bei der Matrizenrechnung wichtig werden, benötigen wir den ersten Faktor als Zeilenvektor und den zweiten als Spaltenvektor. Man sagt auch abkürzend: "Zeilenvektor mal Spaltenvektor". In anderen Lehrbüchern wird das Skalarprodukt auch als "Spaltenvektor mal Spaltenvektor" notiert. Rechnerisch macht das auch tatsächlich keinen großen Unterschied, aber der Zusammenhang von Skalarprodukt und Matrixmultiplikation wird nicht so deutlich.

Definition:
Komponentenweise: $\vec{a}^{\,T} \cdot \vec{b} = \begin{pmatrix}a_1;\, a_2;\, a_3\end{pmatrix} \cdot \begin{pmatrix}b_1\cr b_2\cr b_3\end{pmatrix} = a_1b_1+a_2b_2+a_3b_3$


Geometrisch: $\vec{a}^{\,T} \cdot \vec{b}=\left|\vec{a}\right| \cdot \left|\vec{b}\right| \cdot \cos\left(\varphi\right)$
In Worten: Das Skalarprodukt ist das Produkt der Beträge beider Vektoren und dem Kosinus des kleineren Winkels zwischen $\vec{a}$ und $\vec{b}$ , hier $\varphi$ (gesprochen: "phi") genannt.

Wichtig: Skalarprodukte können immer nur von genau zwei Vektoren berechnet werden, denn das Ergebnis dieser Multiplikation ist ja ein Skalar. Würde man dieses Ergebnis mit einem weiteren Vektor multiplizieren wollen, wäre die Ausgangssituation also nicht mehr "Vektor mal Vektor".


Ein Beispiel:
Gegeben seien $\vec{a}=\dfrac{1}{3}\begin{pmatrix}0\cr-2\cr-7\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}11\cr0\cr3\end{pmatrix}$
Das Skalarprodukt dieser beiden Vektoren ist $\vec{a}^{\,T}\cdot\vec{b}=\dfrac{1}{3}\begin{pmatrix}0;\,-2;\,-7\end{pmatrix} \cdot \begin{pmatrix}11\cr0\cr3\end{pmatrix} = \dfrac{1}{3}\cdot 0\cdot 11+\dfrac{1}{3}\cdot \left(-2\right)\cdot 0+\dfrac{1}{3}\cdot \left(-7\right) \cdot 3 =-7$
Solange wir mit dem Winkel zwischen zwei Vektoren noch nichts anfangen können, hilft uns die geometrische Variante nicht viel. Sie wird aber weiter unten nützlich werden.


Rechengesetze beim Skalarprodukt:
Die Skalarmultiplikation hat - netterweise - mehr oder weniger die Eigenschaften einer "normalen" Multiplikation, z. B. kann man einfach Klammer ausmultiplizieren und das Kommutativ- bzw. Assoziativgesetz anwenden.

Einen bedeutenden Unterschied gibt es aber: Der Satz vom Nullprodukt gilt hier nicht! Das heißt: Das Skalarprodukt zweier Vektoren kann auch dann $0$ sein, wenn beide Vektoren vom Nullvektor verschieden sind. Ein Beispiel: $\begin{pmatrix}3;\,-2\end{pmatrix} \cdot \begin{pmatrix}4\cr6\end{pmatrix} = 3\cdot 4-2\cdot 6 = 0$. Das ist (vermutlich) zunächst überraschend, ergibt sich aber direkt aus der geometrischen Form des Skalarprodukts: Neben den Beträgen der Vektoren spielt ja auch der Kosinus des eingeschlossenen Winkels eine Rolle. Und der Kosinus von $90^\circ$ bzw. $\frac{\pi}{2}$ ist bekanntlich $0$. Geometrisch interpretiert: Die Vektoren stehen also senkrecht (orthogonal) zueinander.
Zusammenfassung: Das Skalarprodukt zweier Vektoren ist genau dann $0$, wenn (mindestens) einer der Vektoren der Nullvektor ist oder die Vektoren einen rechten Winkel einschließen.
Dazu noch eine Vokabel: Ein Vektor, der im rechten Winkel zu einem anderen Vektor (oder auf einem sonstigen geometrischen Objekt) steht, heißt Normalenvektor.


Schauen wir noch an, was passiert, wenn man das Skalarprodukt eines Vektors mit sich selbst berechnet: $\vec{a}^{\,T} \cdot \vec{a} = \left|\vec{a}\right| \cdot \left|\vec{a}\right| \cdot \cos\left(0\right) = \left|\vec{a}\right|^2 \cdot 1 = \left|\vec{a}\right|^2$
Ergebnis: Das Skalarprodukt eines Vektors mit sich selbst ist das Quadrat seines Betrages.
Zieht man daraus die Wurzel, erhält man $\left|\vec{a}\right|=\sqrt{\vec{a}^{\,T} \cdot \vec{a}}$. Daraus folgt, dass das Skalarprodukt eines Vektors mit sich selbst immer dann größer als $0$ ist, wenn der Vektor nicht der Nullvektor ist. Wurzeln aus positiven Werten liefern ja bekanntlich positive Ergebnisse.


Ein Beispiel
Eine kleine Bemerkung vorab: Vektor $\vec{p}$ wird beim ersten Auftreten nur deswegen als Zeilenvektor geschrieben, weil er dann weniger Platz braucht ...
Betrachten wir noch einmal das Rührkuchenbeispiel von oben: $\vec{k_R}^{T}=\begin{pmatrix}0{,}5;\, 0{,}125;\, 3;\, 0{,}2;\, 0{,}2;\, 1\end{pmatrix}$ . Sind nun die Kosten pro Kilogramm Mehl, Liter Milch, Ei, Kilogramm Butter, Kilogramm Zucker und Päckchen Backpulver in dem folgenden Vektor zusammengetragen $\vec{p}^{\,T}=\begin{pmatrix}0{,}79;\, 1{,}09\;\; 0{,}30\;\; 3{,}56\;\; 1{,}20\;\; 0{,}09\end{pmatrix}$ , liefert das Skalarprodukt einen Weg, den Gesamtpreis des Kuchens auszurechnen, nämlich:
$\begin{array}{cclcl} \vec{k}^{\,T}\cdot\vec{p} &=& \begin{pmatrix}0{,}5;\, 0{,}125;\, 3;\, 0{,}2;\, 0{,}2;\, 1\end{pmatrix} \cdot \begin{pmatrix}0{,}79\cr1{,}09\cr0{,}30\cr3{,}56\cr1{,}20\cr0{,}09\end{pmatrix} \cr \cr &=& 0{,}5\cdot 0{,}79 + 0{,}125\cdot 1{,}09 + 3\cdot 0{,}30 + 0{,}2\cdot 3{,}56 + 0{,}2\cdot 1{,}20 + 1\cdot 0{,}09 &\approx& 2{,}47 \end{array}$

Die Zutaten für den Kuchen kosten insgesamt also etwa $2{,}47$ EUR.
Auch wenn man (verständlicherweise) fürs Kuchenbacken normalerweise nicht die Vektorrechnung bemüht, sind die hier aufgezeigten Prinzipien durchaus realistische Anwendungsfälle. Ersetzt man den "Rezeptvektor" durch einen allgemeinen Mengenvektor, ist der Weg vom Kuchenbacken zur innerbetrieblichen Leistungsverrechnung oder zur Produktionsplanung in Unternehmen nicht weit.


Eine Anwendung des Skalarprodukts: Die Berechnung von Winkeln zwischen Vektoren
Ein geometrisches Konzept: Die Ermittlung des Winkels, der von zwei Vektoren eingeschlossen wird.
Wichtig: Dies ist natürlich nur dann sinnvoll möglich, wenn beide Vektoren vom Nullvektor verschieden sind.

Dieser Winkel bzw. sein Kosinus tauchte ja etwas weiter oben bereits auf, nämlich in der Formeln $\vec{a}^{\,T}\cdot\vec{b}=\left|\vec{a}\right| \cdot \left|\vec{b}\right| \cdot \cos\left(\varphi\right)$. Da es ja noch eine zweite Variante gibt, das Skalarprodukt zu berechnen, können wir die beiden Formeln kombinieren: $a_1b_1+a_2b_2+a_3b_3=\left|\vec{a}\right| \cdot \left|\vec{b}\right| \cdot \cos\left(\varphi\right)$
Nach ein bisschen Umstellen erhält man für die Winkelberechnung folgende Formel: $\varphi = \arccos \left( \dfrac{ a_1 b_1 + a_2 b_2 + a_3 b_3}{\sqrt{{a_1}^2+{a_2}^2+{a_3}^2} \cdot \sqrt{{b_1}^2+{b_2}^2+{b_3}^2}} \right) = \arccos \left( \dfrac {\vec{a}^{\,T} \cdot \vec{b}}{\left|\vec{a}\right| \cdot \left|\vec{b}\right|} \right)$

Dieser Winkel liegt zwischen $0^\circ$ und $180^\circ$ bzw. zwischen $0$ und $\pi$.


Zwei Winkelbeispiele:
Betrachten wir noch mal das Beispiel von oben: $\vec{a}=\dfrac{1}{3}\begin{pmatrix}0\cr-2\cr -7\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}11\cr0\cr3\end{pmatrix}$
Das Skalarprodukt dieser beiden Vektoren ist (wie bereits berechnet): $\vec{a}^{\,T}\cdot\vec{b} = -7$
Um den Winkel zwischen diesen Vektoren zu bestimmen, benötigen wir nun noch die Beträge:
$\left|\vec{a}\right| = \sqrt{0+\left(-\dfrac{2}{3}\right)^2+\left(-\dfrac{7}{3}\right)^2} = \dfrac{\sqrt{53}}{3}$
$\left|\vec{b}\right| = \sqrt{11^2+0+3^2} = \sqrt{130}$
Der Winkel $\varphi$ zwischen $\vec{a}$ und $\vec{b}$ ist also: $\varphi = \arccos \left( \dfrac {-7}{\frac{\sqrt{53}}{3} \cdot \sqrt{130}} \right)\approx 104{,}65^\circ$


Und nun - damit wir das Ganze vernünftig zeichnen können - noch ein Beispiel mit 2-komponentigen Vektoren:
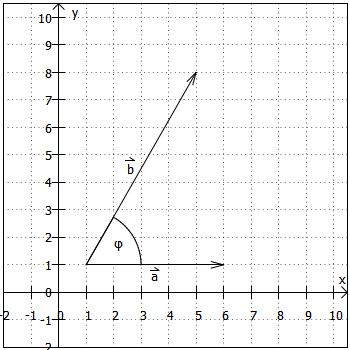
Gegeben seien die Vektoren $\vec{a}=\begin{pmatrix}5\cr0\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}4\cr7\end{pmatrix}$
Das Skalarprodukt dieser beiden Vektoren ist: $\vec{a}^{\,T}\cdot\vec{b} = 5\cdot 4+0\cdot 7$
Um den Winkel zwischen diesen Vektoren zu bestimmen, benötigen wir nun noch die Beträge:
$\left|\vec{a}\right| = \sqrt{5^2+0} = 5$
$\left|\vec{b}\right| = \sqrt{4^2+7^2} = \sqrt{65}$
Der Winkel $\varphi$ zwischen $\vec{a}$ und $\vec{b}$ ist also: $\varphi = \arccos \left( \dfrac {20}{5 \cdot \sqrt{65}} \right)\approx 60{,}26^\circ$
In einer Grafik sieht das dann so aus:

 

 

Die beiden folgenden Produkte von Vektoren sind in erster Linie für Ingenieurstudierende relevant.

 

Vektorprodukt

Um das Vektorprodukt vom Skalarprodukt unterscheiden zu können, wird hier ein anderes Zeichen benutzt, nämlich $\times$. Wegen dieses Zeichens wird das Vektorprodukt auch Kreuzprodukt genannt. Manchmal nennt man es auch äußeres Produkt. Die Bezeichnung "Vektorprodukt" gibt aber - wie Skalarprodukt - von vorneherein ganz klar an, wie das Ergebnis aussieht. Daher verwende ich hier diesen Begriff.

Wichtig vorab: Das Vektorprodukt gibt es in dieser Form nur für dreidimensionale Vektoren!


Definition:
Komponentenweise: $\vec{a} \times \vec{b} = \begin{pmatrix}a_1\cr a_2\cr a_3\end{pmatrix} \times \begin{pmatrix}b_1\cr b_2\cr b_3\end{pmatrix} = \begin{pmatrix}a_2b_3-a_3b_2 \cr a_3b_1-a_1b_3 \cr a_1b_2 - a_2b_1\end{pmatrix}$
Das sieht zunächst reichlich verwirrend aus ... Um sich die Formel zu merken, gibt es eine Eselsbrücke, die auch "Schnürsenkelprinzip" genannt wird:
Dazu schreibt man 1. die Komponenten der beiden Vektoren jeweils zweimal untereinander, streicht als 2. die erste und die letzte Zeile und subtrahiert dann als 3. die entstehenden Produkte über Kreuz:

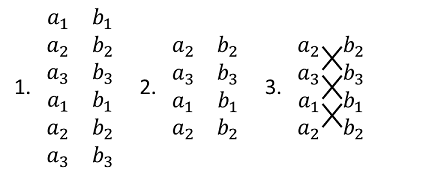
Es werden also in jeder Zeile des Ergebnisses genau die anderen Zeilen der Ausgangsvektoren verknüpft: in der ersten Ergebniszeile die Elemente aus der 2. und 3. Zeile der Ausgangsvektoren etc. Zudem unterscheiden sich Minuend und Subtrahend im Ergebnis nur durch die Reihenfolge der Indizes.

Später werden Sie evtl. noch eine Möglichkeit kennenlernen, Vektorprodukte zu berechnen - allerdings muss man dazu mit Determinanten umgehen können.


Geometrisch: Vom geometrischen Standpunkt aus ist es ja immer wichtig, von einem Vektor Betrag, Richtung und Orientierung zu kennen. Da das Vektorprodukt nun mal einen Vektor als Ergebnis liefert, müssen diese Fragen auch hier beantwortet werden:
Der Betrag des Vektorprodukts entspricht der Fläche des Parallelogramms, das von $\vec{a}$ und $\vec{b}$ aufgespannt wird, also: $\left|\vec{a} \times \vec{b}\right|=\left|\vec{a}\right|\cdot\left|\vec{b}\right|\cdot\sin\left(\varphi\right)$ , wobei $\varphi$ der kleinere Winkel ist, der zwischen $\vec{a}$ und $\vec{b}$ liegt.
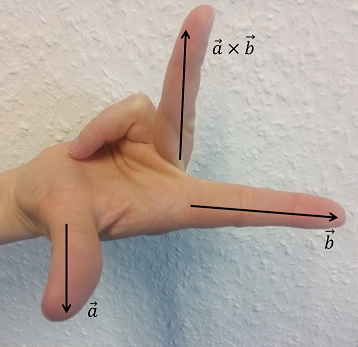
Zu Richtung und Orientierung: $\vec{a}\times\vec{b}$ steht im rechten Winkel zu $\vec{a}$ und $\vec{b}$. Zusammen bilden die Vektoren $\vec{a}$, $\vec{b}$ und ihr Vektorprodukt ein so genanntes Rechte-Hand-System, in dem sich $\vec{a}$ , $\vec{b}$ und $\vec{a}\times\vec{b}$ wie Daumen, Zeigefinger und Mittelfinger der rechten Hand verlaufen. Damit ist dann auch die Orientierung festgelegt.

Rechengesetze beim Vektorprodukt:
Anders als beim Skalarprodukt gelten für das Vektorprodukt Rechenregeln, die uns (noch) nicht so vertraut sind:

• Das Vektorprodukt eines Vektors mit sich selbst ist immer der Nullvektor. In einer Formel: $\vec{a}\times\vec{a}=\vec{0}$. Etwas Allgemeiner gilt: $\vec{a}\times\vec{b} =\vec{0}$ genau dann, wenn $\vec{a}$ und $\vec{b}$ parallel bzw. antiparallel sind oder wenn (mindestens) einer der Vektoren der Nullvektor ist. Geometrisch passt das: In all diesen Fällen wird von den Vektoren kein Parallelogramm aufgespannt.
  
  
• Das Vektorprodukt ist nicht kommutativ, sondern antikommutativ (auch antisymmetrisch genannt): $\vec{a}\times\vec{b} = -\left(\vec{b}\times\vec{a}\right)$ (Bitte das Minuszeichen nicht übersehen!)
  
  
• Das Assoziativgesetz gilt nur, wenn ein Skalar $\lambda\in\mathbb{R}$ beteiligt ist: $\left(\lambda\vec{a}\right)\times\vec{b} = \lambda\left(\vec{a}\times\vec{b}\right)=\vec{a}\times\left(\lambda\vec{b}\right)$. Für drei Vektoren gilt es (im Allgemeinen) nicht!
  
  
• Immerhin das Distributivgesetz gilt in seiner gewohnten Form: $\left(\vec{a}+\vec{b}\right)\times\vec{c} = \vec{a}\times\vec{c}+\vec{b}\times\vec{c}$ bzw. $\vec{a}\times\left(\vec{b}+\vec{c}\right)=\vec{a}\times\vec{b}+\vec{a}\times\vec{c}$

Ein Rechenbeispiel:
Gegeben seien $\vec{a} = \begin{pmatrix}1\cr-1\cr4\end{pmatrix}$ und $\vec{b} = \begin{pmatrix}2\cr-3\cr0\end{pmatrix}$
Das Vektorprodukt dieser Vektoren ist $\vec{a} \times \vec{b} = \begin{pmatrix}1\cr-1\cr4\end{pmatrix} \times \begin{pmatrix}2\cr-3\cr0\end{pmatrix} = \begin{pmatrix}-1\cdot 0 - 4\cdot\left(-3\right) \cr 4\cdot 2 - 1\cdot 0 \cr 1\cdot \left(-3\right) - \left(-1\right)\cdot 2\end{pmatrix} = \begin{pmatrix}12\cr8\cr-1\end{pmatrix}$


Anwendung: Physiker bzw. Ingenieure nutzen Vektorprodukte beispielsweise, um die Feldstärke von Magnetfeldern zu bestimmen. In der BWL kommt man üblicherweise ohne Vektorprodukte aus.

 

Spatprodukt

Kommen wir zum letzten Produkt von Vektoren: Da das Spatprodukt eine Kombination aus Skalar- und Vektorprodukt ist, wird meist kein eigenes Symbol dafür eingeführt. Man nennt das Spatprodukt (aus leicht einsehbaren Gründen) auch gemischtes Produkt.

Wichtig vorab 1: Da ein Vektorprodukt berechnet wird, müssen die Vektoren jeweils drei Komponenten haben.
Wichtig vorab 2: Da ein Skalarprodukt berechnet wird, ist das Ergebnis ein Skalar.


Definition:
Komponentenweise: $\vec{a}^{\,T}\cdot \left(\vec{b} \times \vec{c}\right)$
Bitte achten Sie darauf, dass die Klammern genauso gesetzt werden müssen. $\left(\vec{a}^{\,T}\cdot \vec{b}\right) \times \vec{c}$ würde nicht funktionieren, weil $\vec{a}^{\,T}\cdot \vec{b}$ ja einen Skalar als Ergebnis hat. Aus diesem Skalar und dem Vektor $\vec{c}$ kann aber kein Vektorprodukt berechnet werden.

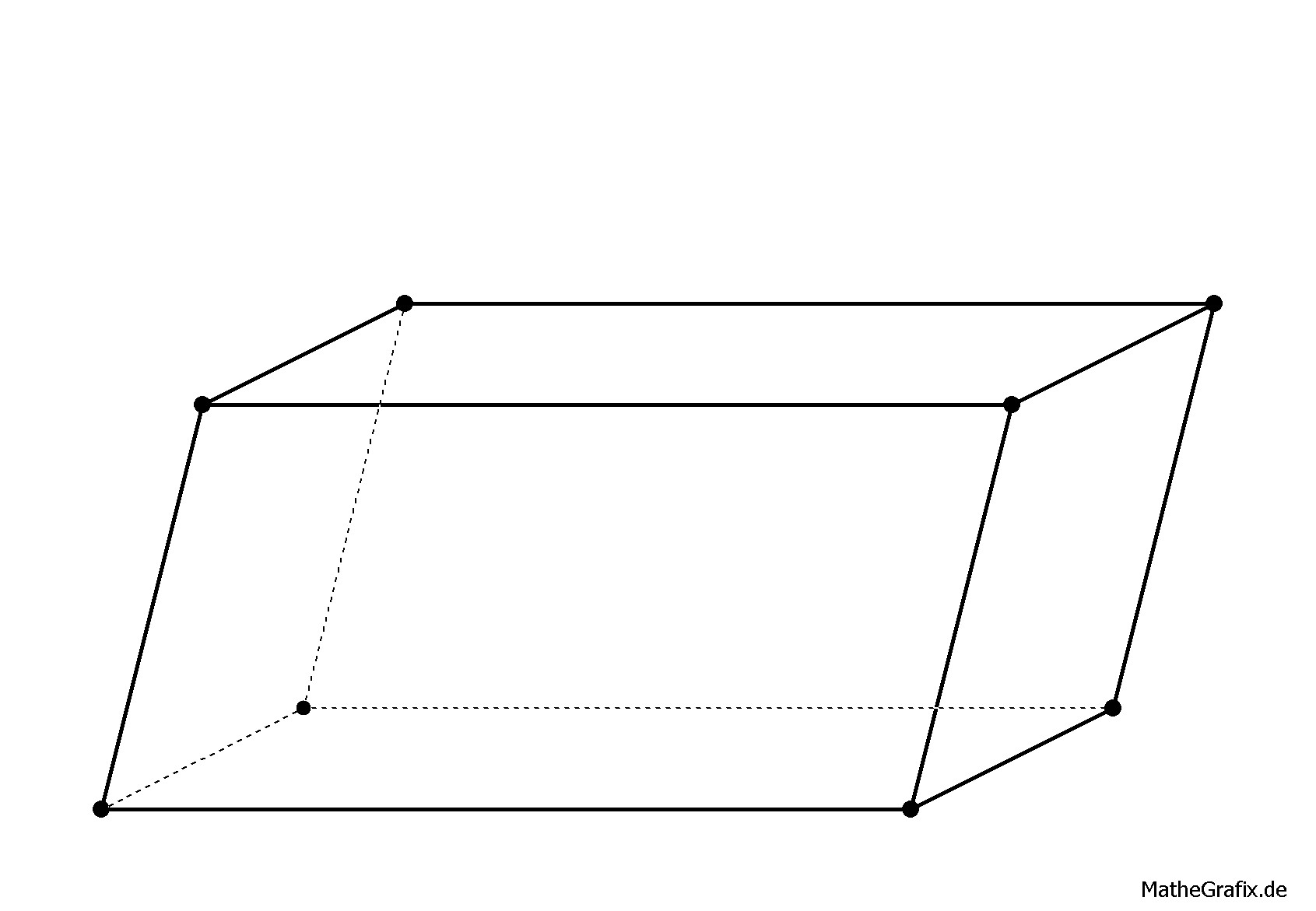
Geometrisch: In den geometrischen Betrachtungen steckt gleichzeitig die Erklärung, was man mit dem Spatprodukt anfangen kann. Dafür müssen wir zunächst die Frage klären, was ein Spat im mathematischen Sinne (man sagt dazu auch Parallelepiped) ist: Es handelt sich um ein Art dreidimensionales Parallelogramm, das von drei Vektoren im Raum aufgespannt wird (siehe Grafik rechts). Mithilfe des Spatprodukts kann man das Volumen eines solchen Spats bestimmen: $V_{Spat} = \left|\vec{a}^{\,T}\cdot\left(\vec{b}\times\vec{c}\right)\right|$ . Es fügt sich in dieser Hinsicht gut an das Vektorprodukt an, mit dem ja die Fläche eines Parallelogramms berechnet werden kann. Und wie beim Vektorprodukt spielt auch hier die Orientierung eine Rolle, wenn wir auf den Betrag verzichten: Ist das Spatprodukt positiv, bilden $\vec{a}$, $\vec{b}$ und $\vec{c}$ (in dieser Reihenfolge) ein Rechtssystem. Ist das Spatprodukt negativ, bilden $\vec{a}$, $\vec{b}$ und $\vec{c}$ (in dieser Reihenfolge) ein Linkssystem. Man spricht daher auch vom orientierten Volumen (ähnlich dem orientierten Flächeninhalt bei Integralen).


Ein Beispiel:
Gegeben seien $\vec{a}=\begin{pmatrix}2\cr-6\cr1\end{pmatrix}$ , $\vec{b}=\begin{pmatrix}5\cr-1\cr-10\end{pmatrix}$ und $\vec{c}=\begin{pmatrix}-3\cr0\cr-1\end{pmatrix}$
Das Spatprodukt dieser Vektoren ist
$\begin{array}{rcl} \vec{a}^{\,T}\cdot\left(\vec{b} \times \vec{c}\right) &=& \begin{pmatrix}2;\,-6;\,1\end{pmatrix}\cdot\left(\begin{pmatrix}5\cr-1\cr-10\end{pmatrix} \times \begin{pmatrix}-3\cr0\cr-1\end{pmatrix}\right) \cr &=& \begin{pmatrix}2;\,-6;\,1\end{pmatrix}\cdot\begin{pmatrix}-1\cdot \left(-1\right) - \left(-10\right)\cdot 0 \cr -10\cdot \left(-3\right) - 5\cdot \left(-1\right) \cr 5\cdot 0 - \left(-1\right)\cdot \left(-3\right)\end{pmatrix} \cr &=& \begin{pmatrix}2;\,-6;\,1\end{pmatrix}\cdot\begin{pmatrix}1\cr35\cr-3\end{pmatrix} \cr &=& 2\cdot 1 + \left(-6\right)\cdot 35 - 3 = -211 \end{array}$


Rechengesetze beim Spatprodukt:

• Da das Vektorprodukt eines Vektors mit sich selbst der Nullvektor und das Skalarprodukt eines beliebigen Vektors mit dem Nullvektor $0$ ist, ist auch $\vec{a}^{\,T}\cdot\left(\vec{b}\times\vec{b}\right) = 0$.
  
  
• Dass das Spatprodukt nicht kommutativ ist, ist relativ naheliegend, weil das Vektorprodukt es ja auch nicht ist. Allerdings gibt es hier stattdessen eine wirklich spannende Eigenschaft: Der Wert des Spatprodukts ändert sich nicht, wenn man die Faktoren zyklisch durchtauscht: $\vec{a}^{\,T}\cdot\left(\vec{b}\times\vec{c}\right) = \vec{c}^{\,T}\cdot\left(\vec{a}\times\vec{b}\right) = \vec{b}^{\,T}\cdot\left(\vec{c}\times\vec{a}\right)$.
  
  
• Ebenso wie das Vektorprodukt ist das Spatprodukt nicht assoziativ. Eine Art Assoziativgesetz gilt aber für Skalare: $\lambda\vec{a}^{\,T}\cdot\left(\vec{b}\times\vec{c}\right) = \vec{a}^{\,T}\cdot\left(\lambda\vec{b}\times\vec{c}\right) = \vec{a}^{\,T}\cdot\left(\vec{b}\times\lambda\vec{c}\right) = \vec{a}^{\,T}\cdot\left(\vec{b}\times\vec{c}\right)\cdot\lambda$. Anders formuliert: Multipliziert man einen der Vektoren mit einem Skalar, kann man diesen quasi aus dem Spatprodukt "ausklammern".
  
  
• Noch ein Klassiker zum Abschluss - das Distributivgesetz: $\left(\vec{a}+\vec{b}\right)^{\,T}\cdot\left(\vec{c}\times\vec{d}\right) = \vec{a}^{\,T}\cdot\left(\vec{c}\times\vec{d}\right) + \vec{b}^{\,T}\cdot\left(\vec{c}\times\vec{d}\right)$

Einen Sonderfall müssen wir noch betrachten, nämlich $\vec{a}^{\,T}\cdot\left(\vec{b} \times \vec{c}\right)=0$. Dann muss das Volumen des betrachteten Spats $0$ sein, was entweder passiert, wenn einer der Vektoren der Nullvektor ist oder die drei Vektoren in einer Ebene liegen (dann kann ja kein 3-dimensionales Gebilde entstehen). Das heißt, man kann mithilfe des Spatprodukts feststellen, ob drei gegebene Vektoren komplanar (in anderen Worten: linear abhängig) sind. Dieser Rechenweg ist manchmal einfacher, als der im Abschnitt "Lineare Unabhängigkeit" beschriebene.

 

Ausblick

Mathematisch kann man eine Menge mit Vektoren machen, was überhaupt nichts mehr mit Geometrie und Pfeilen zu tun hat. Das ist ja durchaus typisch für die Mathematik: Hat man in einem Bereich etwas Nützliches gefunden, sucht man nach Möglichkeiten, dieses Prinzip auf andere Bereiche zu übertragen.

Der ganz oben erwähnte Vektorraum ist ein Beispiel dafür: Ausgehend von Vektoren wurde ein (abstraktes) Konzept entwickelt, welches u. a. auf Funktionen angewendet werden kann. Das klingt zunächst vielleicht komisch, ist aber sehr praktisch. Wurde nämlich gezeigt, dass eine Menge von Funktionen einen Vektorraum bildet, weiß man, dass die Funktionen bestimmte Eigenschaften haben (müssen) und dass bestimmte Rechenverfahren problemlos angewendet werden können. Man muss dies also nicht für jede Eigenschaft und jedes Rechenverfahren einzeln überprüfen.

Etwas naheliegender sind natürlich Matrizen und Determinanten. Diese können beispielsweise beim Lösen linearer Gleichungssysteme, die ja in vielen Zusammenhängen auftreten, eingesetzt werden. Darauf baut z. B. auch der Simplex-Algorithmus zum Lösen linearer Optimierungsprobleme auf. Nach vielen militärischen Anwendungsfällen wird dieses Verfahren heute im Rahmen des Operations Research vor allem in Unternehmen eingesetzt, um herauszufinden, wie die gegebenen Mittel eingesetzt werden müssen, um das beste aller möglichen Ergebnisse zu erreichen.

Sie sehen, das Feld, in dem Vektoren zum Einsatz kommen, ist vielfältig. Damit Sie Vektoren später für die eigentlich spannenden Dinge nutzen können, wurden in diesem Kapitel die Grundlagen gelegt, ohne die es - wie immer - nicht geht.