Übersicht:

• Lösung zur 1. Aufgabe
• Lösung zur 2. Aufgabe
• Lösung zur 3. Aufgabe
• Lösung zur 4. Aufgabe
• Lösung zur 5. Aufgabe

16.3 Exponentialgleichungen und -funktionen - Lösungen

Eine Bemerkung vorab: Bei vielen Aufgaben könnte man auch einen Logarithmus zu einer anderen Basis nehmen. Es gilt nämlich z. B.: $\dfrac{\ln(15)}{\ln(26)} = \dfrac{\lg(15)}{\lg(26)} \approx 0{,}83$

1. Aufgabe

1)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr\cr 26^x &=& 15 &\vert& \ln() \cr \ln(26^x) &=& \ln(15) &\vert& \text{3. Logarithmengesetz} \cr x \cdot \ln(26) &=& \ln(15) &\vert& :\ln(26) \cr x &=& \dfrac{\ln(15)}{\ln(26)} \approx 0{,}83 \cr\cr \mathbb{L} &=& \left\{\dfrac{\ln(15)}{\ln(26)}\right\} \end{array}$

Bemerkung: Die Darstellung $\dfrac{\ln(15)}{\ln(26)}$ des Ergebnisses ist die mathematisch beste, weil sie exakt ist. Wer das Ergebnis lieber als Dezimalzahl hat, sollte erst ganz am Ende umformen und runden, da die Rundungsfehler sonst zu groß werden.
 

2)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \\\\ 2^{5+x} &=& 8^x \\2^{5+x} &=& \left(2^3\right)^x \\2^{5+x} &=& 2^{3x} &\vert& \text{ld}() \\5+x &=& 3x &\vert& -x \\5 &=& 2x &\vert& :2 \\\dfrac{5}{2} &=& x \\\\\mathbb{L} &=& \left\{\dfrac{5}{2}\right\}\end{array}$
 

3)
$\begin{array}{rclcl}\mathbb{D} &=& \mathbb{R} \cr\cr 27^x+4 &=& 0 &\vert& -4 \cr 27^x &=& -4 \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, hat diese Gleichung keine Lösung: $\mathbb{L} = \emptyset$

4)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr \cr e^{2x+3} &=& 2 \cdot e^x &\vert& \ln() \cr \ln\left(e^{2x+3}\right) &=& \ln\left(2 \cdot e^x\right) &\vert& \text{1. Logarithmengesetz} \cr 2x+3 &=& \ln\left(2\right) + \ln\left(e^x\right) \cr 2x+3 &=& \ln(2)+x &\vert& -x -3 \cr x &=& \ln(2)-3 \approx -2{,}31 \cr \cr \mathbb{L} &=& \left\{\ln(2)-3\right\} \end{array}$
 

5)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr \cr 10^x &=& 100^{x+1} \cr 10^x &=& \left(10^2\right)^{x+1} &\vert& \text{5. Potenzgesetz} \cr 10^x &=& 10^{2(x+1)} &\vert& \lg() \cr \lg\left(10^x\right) &=& \lg\left(10^{2(x+1)}\right) \cr x &=& 2(x+1) \cr x &=& 2x+2 &\vert& -2x \cr -x &=& 2 &\vert& \cdot (-1) \cr x &=& -2 \cr \cr \mathbb{L} &=& \{-2\} \end{array}$

6)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr \cr 11^{x+2} &=& 8 &\vert& \ln() \cr \ln\left(11^{x+2}\right) &=& \ln(8) &\vert& \text{3. Logarithmengesetz} \cr (x+2)\ln(11) &=& \ln(8) &\vert& : \ln(11) \cr x+2 &=& \dfrac{\ln(8)}{\ln(11)} &\vert& -2 \cr x &=& \dfrac{\ln(8)}{\ln(11)}-2 \approx -1{,}13 \cr \cr \mathbb{L} &=& \left\{ \dfrac{\ln(8)}{\ln(11)} - 2\right\} \end{array}$
 

7)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr \cr 1{,}06^{x-1} &=& 2{,}08^x &\vert& \ln() \cr \ln\left(1{,}06^{x-1}\right) &=& \ln\left(2{,}08^x\right) &\vert& \text{3. Logarithmengesetz} \cr (x-1)\ln(1{,}06) &=& x\ln(2{,}08) \cr x\ln(1{,}06)-\ln(1{,}06) &=& x\ln(2{,}08) &\vert& +\ln(1{,}06)-x\ln(2{,}08) \cr x\ln(1{,}06)-x\ln(2{,}08) &=& \ln(1{,}06) \cr x\left(\ln(1{,}06)-\ln(2{,}08)\right) &=& \ln(1{,}06) &\vert& : \left(\ln(1{,}06)-\ln(2{,}08)\right) \cr x &=& \dfrac{\ln(1{,}06)}{\ln(1{,}06)-\ln(2{,}08)} \approx -0{,}09 \cr \cr \mathbb{L} &=& \left\{\dfrac{\ln(1{,}06)}{\ln(1{,}06)-\ln(2{,}08)}\right\} \end{array}$

Bemerkung: Auch wenn es vielleicht nicht so aussieht: Ab der dritten Zeile ist die Ursprungsgleichung auf eine lineare Gleichung zurückgeführt. Es wird ab diesem Zeitpunkt keine Umformung oder Rechenoperation benötigt, die nicht schon im Kapitel 5 eingeführt worden ist. Die Gleichung lässt sich also ziemlich unkompliziert lösen - ok, die Koeffizienten sind etwas unhandlich ...
 

8)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr \cr 17^s &=& e &\vert& \ln() \cr \ln(17^s) &=& \ln(e) &\vert& \text{3. Logarithmengesetz} \cr s \cdot \ln(17) &=& 1 &\vert& : \ln(17) \cr s &=& \dfrac{1}{\ln(17)} \approx 0{,}35 \cr \cr \mathbb{L} &=& \left\{\dfrac{1}{\ln(17)}\right\} \end{array}$
 

9)
$\begin{array}{rclcl}\mathbb{D} &=& \mathbb{R} \cr \cr 66^y &=& 1 & \vert & \ln() \cr \ln(66^y) &=& \ln(1) &\vert& \text{3. Logarithmengesetz} \cr y \cdot \ln(66) &=& 0 & \vert & :\ln(66) \cr y &=& 0 \cr \cr \mathbb{L} &=& \left\{0\right\}\end{array}$
 

10)
$\begin{array}{rclcl}\mathbb{D} &=& \mathbb{R} \cr \cr 48^{\frac{1}{18}x-39} &=& 48 &\vert& \log_{48}() \cr \dfrac{1}{18}x-39 &=& 1 &\vert& +39 \cr \dfrac{1}{18}x &=& 40 &\vert& : \dfrac{1}{18} \cr x &=& 720 \cr \cr \mathbb{L} &=& \left\{720\right\}\end{array}$
 

11)
$\begin{array}{rclcl}\mathbb{D} &=& \mathbb{R} \cr \cr -33+5^{3x-7} &=& 12 &\vert& +33 \cr 5^{3x-7} &=& 45 &\vert& \ln() \cr \ln(5^{3x-7}) &=& \ln(45) &\vert& \text{3. Logarithmengesetz} \cr \left(3x-7 \right)\ln(5) &=& \ln(5 \cdot 9) &\vert& \text{1. Logarithmengesetz} \cr 3x \cdot \ln(5) - 7\ln(5) &=& \ln(5) + \ln(9) &\vert& +7\ln(5) \cr 3x\ln(5) &=& 8\ln(5) + \ln(3^2) &\vert& : 3\ln(5) \cr x &=& \dfrac{8\ln(5) + 2\ln(3)}{3\ln(5)} \approx 3{,}12 \cr \cr \mathbb{L} &=& \left\{\dfrac{8\ln(5) + 2\ln(3)}{3\ln(5)}\right\}\end{array}$

12)
$\begin{array}{rclcl}\mathbb{D} &=& \mathbb{R} \cr \cr 7 \cdot e^{15x^2-30x} &=& 21 &\vert& :7 \cr e^{15x^2-30x} &=& 3 &\vert& \ln() \cr 15x^2-30x &=& \ln(3) &\vert& :15 \cr x^2-2x &=& \dfrac{\ln(3)}{15} &\vert& - \dfrac{\ln(3)}{15} \cr x^2-2x-\dfrac{\ln(3)}{15} &=& 0 &\vert&\text{p-q-Formel} \cr x_{1,2} &=& 1\pm\sqrt{1+\dfrac{\ln(3)}{15}} \cr\cr x_1 &=& 1+\sqrt{1+\dfrac{\ln(3)}{15}} \approx 2{,}04 \cr x_2 &=& 1-\sqrt{1+\dfrac{\ln(3)}{15}} \approx -0{,}04 \cr \cr \mathbb{L} &=& \left\{1+\sqrt{1+\dfrac{\ln(3)}{15}};\,1-\sqrt{1+\dfrac{\ln(3)}{15}}\right\}\end{array}$
 

13)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr\cr 5^{2t}-16\cdot 5^t &=& 0 &\vert& \text{3. Potenzgesetz} \cr \left(5^t\right)^2-16\cdot 5^t &=& 0 \end{array}$

Substitution: $u=5^t$
$\begin{array}{crclcl} & u^2-16u &=& 0 \cr & u\left(u-16 \right) &=& 0 \cr \text{Faktor 1: } & u_1 &=& 0 \cr\cr \text{Faktor 2: } & u -16 &=& 0 \cr & u_2 &=& 16\end{array}$

Rücksubstitution:
$\begin{array}{rclcl} u_1 = 5^{t_1} &=& 0 \cr\cr u_2 = 5^{t_2} &=& 16 &\vert&\ln() \cr \ln(5^t_2) &=& \ln(16) &\vert& \text{3. Logarithmengesetz} \cr t_2 \cdot \ln(5) &=& \ln(16) &\vert&:\ln(5) \cr t_2 &=& \dfrac{\ln(16)}{\ln(5)} \approx1{,}72 \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert die Rücksubstitution von $u_1$ keine weiteren Lösungen: $\mathbb{L} = \left\{\dfrac{\ln(16)}{\ln(5)}\right\}$

14)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr\cr 4 \cdot e^{25x+18}-1 &=& 51 &\vert& +1 \cr 4 \cdot e^{25x+18} &=& 52 &\vert& :4 \cr e^{25x+18} &=& 13 &\vert& \ln() \cr \ln(e^{25x+18}) &=& \ln(13) \cr 25x+18 &=& \ln(13) &\vert& -18 \cr 25x &=& \ln(13)-18 &\vert& :25 \cr x &=& \dfrac{\ln(13)-18}{25} \approx -0{,}62 \cr\cr \mathbb{L}&=&\left\{\dfrac{\ln(13)-18}{25}\right\} \end{array}$
 

15)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr\cr e^x \cdot e^{2x} -e^{18} &=& 0 &\vert& \text{1. Potenzgesetz} \cr e^{x+2x} -e^{18} &=& 0 &\vert& +e^{18} \cr e^{3x} &=& e^{18} &\vert& \ln() \cr 3x &=& 18 &\vert& :3 \cr x &=& 6 \cr\cr \mathbb{L}&=&\left\{6\right\} \end{array}$

16)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr\cr 2^{5z^2} \cdot 2^{95z-45} \cdot 2^{-55} &=& 1 &\vert& \text{1. Potenzgesetz} \cr 2^{5z^2+(95z-45)-55} &=& 1 &\vert& \text{ld()} \cr 5z^2 + 95z -100 &=& 0 &\vert& :5 \cr z^2+19z-20 &=& 0 &\vert&\text{p-q-Formel} \cr z_{1,2} &=& -\dfrac{19}{2} \pm \sqrt{\left(\dfrac{19}{2}\right)+20} \cr &=& -\dfrac{19}{2} \pm \sqrt{\dfrac{441}{4}} \cr\cr z_1 &=& -\dfrac{19}{2} + \dfrac{21}{2} = 1 \cr z_2 &=& -\dfrac{19}{2} - \dfrac{21}{2} =-20 \cr\cr \mathbb{L}&=&\left\{-20; 1\right\} \end{array}$

17)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr\cr \dfrac{1.000^{x+1}}{10^{5x}}-12 &=& 43 &\vert& \text{5. Potenzgesetz} \cr\cr \dfrac{\left(10^3\right)^{x+1}}{10^{5x}}-12 &=& 43 &\vert& \text{2. Potenzgesetz} \cr\cr 10^{3x+3-5x}-12 &=& 43 &\vert& +12 \cr 10^{-2x+3} &=& 55 &\vert& \lg() \cr -2x+3 &=& \lg(55) &\vert& -3 \cr -2x &=& \lg(55)-3 &\vert& :(-2) \cr x &=& \dfrac{\lg(55)-3}{-2} \approx 0{,}63 \cr\cr \mathbb{L}&=&\left\{\dfrac{\lg(55)-3}{-2}\right\} \end{array}$

18)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr\cr 2 \cdot 10^{2x}-16 \cdot 10^x+30 &=& 0 &\vert& \text{3. Potenzgesetz} \cr 2 \cdot \left(10^x \right)^2 -16 \cdot 10^x+30 &=& 0 \end{array}$

Substitution: $u=10^x$
$\begin{array}{rclcl} 2u^2 -16u+30 &=& 0 &\vert& :2 \cr u^2-8u+15 &=& 0 &\vert& \text{p-q-Formel} \cr u_{1,2} &=& 4\pm \sqrt{16-15} \cr u_{1,2} &=& 4\pm \sqrt{1}\cr\cr u_1 &=& 4+1 = 5 \cr u_2 &=& 4-1 = 3\end{array}$

Rücksubstitution:
$\begin{array}{rclcl} u_1 = 10^{x_1} &=& 5 &\vert& \lg() \cr x_1 &=& \lg(5) \approx 0{,}70 \cr\cr u_2 = 10^{x_2} &=& 3 &\vert& \lg() \cr x_2 &=& \lg(3) \approx 0{,}48 \cr\cr\mathbb{L}&=&\left\{\lg(3); \lg(5) \right\}\end{array}$

19)
$\begin{array}{rclcl} \mathbb{D} &=& \mathbb{R} \cr\cr -9 \cdot e^{4x}+45 \cdot e^2x &=& 0 &\vert& \text{3. Potenzgesetz} \cr -9 \cdot \left(e^{2x} \right)^2+45 \cdot e^{2x} &=& 0 \end{array}$

Substitution: $u=e^{2x}$
$\begin{array}{crclcl} & -9u^2+45u &=& 0 \cr & 9u(-u+5) &=& 0 \cr \text{Faktor 1:} & u_1 &=& 0 \cr\cr \text{Faktor 2:} & -u+5 &=& 0 \cr & u_2 &=& 5\end{array}$

Rücksubstitution:
$\begin{array}{rclcl} u_1 = e^{2x_1} &=& 0 \cr\cr u_2 = e^{2x_2} &=& 5 &\vert& \ln() \cr 2x_2 &=& \ln(5) &\vert& :2 \cr x_2 &=& \dfrac{\ln(5)}{2} \approx 0{,}80 \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert die Rücksubstitution von $u_1$ keine weiteren Lösungen: $\mathbb{L} = \left\{\dfrac{\ln(5)}{2}\right\}$

20)
$\begin{array}{crclcl}& \mathbb{D} &=& \mathbb{R} \\\\& 3\left(\dfrac{1}{3} x^2-112\right) e^{2x+6} &=& -\dfrac{109x}{e^{-2x-6}} \\\\& \left(x^2-336\right) e^{2x+6} &=& -109x\cdot e^{-(-2x-6)} &\vert& +109xe^{2x+6}\\\\& \left(x^2-336\right) e^{2x+6} +109xe^{2x+6} &=& 0\\\\& \left(x^2+109x-336\right) e^{2x+6} &=& 0 &\vert& \text{Satz vom Nullprodukt} \\\\\text{Faktor 1:} & x^2+109x-336 &=& 0 &\vert & \text{p-q-Formel} \\\\& x_{1,2} &=& -\dfrac{109}{2}\pm \sqrt{\left(\dfrac{109}{2}\right)^2+336} \\\\& x_{1,2} &=& -\dfrac{109}{2}\pm \sqrt{\dfrac{13.225}{4}} \\\\& x_{1} &=& -\dfrac{109}{2}+\dfrac{115}{2} = 3 \\\\& x_{2} &=& -\dfrac{109}{2}-\dfrac{115}{2} = -112 \\\\\\\text{Faktor 2:} & e^{2x+6} &=& 0\end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert der zweite Faktor keine weiteren Lösungen: $\mathbb{L} = \{-112;3\}$

2. Aufgabe

Sei $x$ die Anzahl der Jahre.
Dann lautet die Gleichung, die zu lösen ist: $1.000 \cdot 1{,}025^x=5.000$

$\begin{array}{rclcl} 1.000 \cdot 1{,}025^x &=& 5.000 &\vert& :1.000 \cr 1{,}025^x &=& 5 &\vert& \ln() \cr \ln\left(1{,}025^x\right) &=& \ln(5) &\vert& \text{3. Logarithmengesetz} \cr x\cdot \ln(1{,}025) &=& \ln(5) &\vert& : \ln(1{,}025) \cr x &=& \dfrac{\ln(5)}{\ln(1{,}025)} \approx 65{,}18 \end{array}$

Nach ungefähr $65{,}18$ Jahren beträgt das Kapital insgesamt $5.000$ EUR.

3. Aufgabe

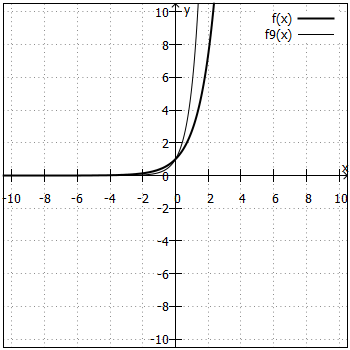
Der Übersicht wegen sind immer nur zwei Graphen in ein Koordinatensystem eingezeichnet. Zusätzlich zu $f_1(x)$ bis $f_{12}(x)$ wurde jeweils $f(x)=e^x$ (fett gedruckt) mit abgebildet, um einen besseren Vergleich zu haben.

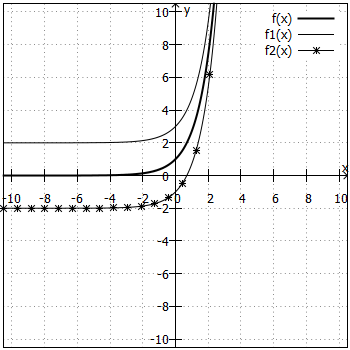
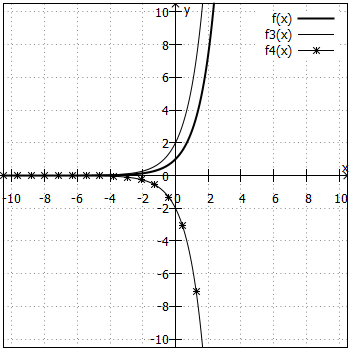
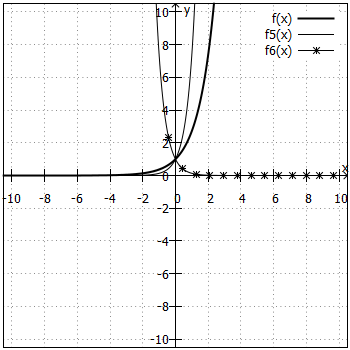
$f_5(x)$ und $f_6(x)$ sind achsensymmetrisch zur y-Achse. Dies gilt allgemein für $f(x)=a^x$ und $f(x)=\left(\frac{1}{a}\right)^x=a^{-x}$.

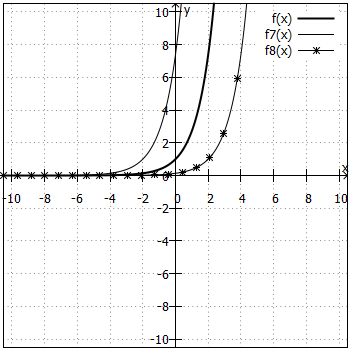
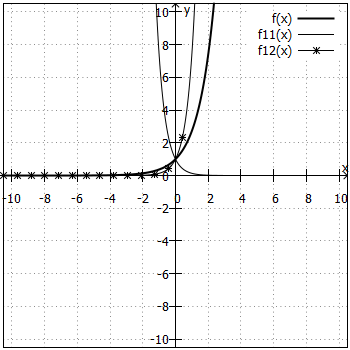
Was ist mit $f_{10}(x)$?
$f_{10}(x)=(-2e)^x$ hat eine negative Basis, und Potenzen mit negativen Basen sind im Bereich der reellen Zahlen nur für ganzzahlige Exponenten definiert, weil sonst Wurzeln aus negativen Zahlen gezogen werden müssen, z. B. ist ja $(-2e)^\frac{1}{2}=\sqrt{-2e}$ nicht definiert. Da Funktionen üblicherweise für die reellen Zahlen (oder Teilbereiche davon) definiert sind, gäbe es hier also für beliebig viele x-Werte keinen Funktionswert. Daher beschreibt $f_{10}(x)$ keine Funktion.

Die Graphen von $f_{11}(x)$ und $f_{12}(x)$ sollten Ihnen bekannt vorkommen, denn sie sind bereits im dritten Koordinatensystem von oben mit den Funktionsgraphen von $f_5(x)$ und $f_6(x)$ zu sehen gewesen. Ist es überraschend, dass zwei unterschiedlich aussehende Funktionsterme den gleichen Graphen haben? Nein, denn nach dem Potenzgesetzen gilt:

$f_5(x)=e^{2x}=\dfrac{1}{e^{-2x}}=f_{12}(x)$
und
$f_6(x)=e^{-2x}=\dfrac{1}{e^{2x}}=f_{11}(x)$

4. Aufgabe

1)
a)
$\begin{array}{rclll} f(0) &=& \dfrac{5^{0-1}}{10} &=& \dfrac{1}{50} \quad \rightarrow \quad P_1\left(0 \mid \dfrac{1}{50}\right) \end{array}$

b)
$\begin{array}{rclll} 0{,}2 &=& \dfrac{5^{x-1}}{10} &\vert & \cdot 10 \cr 2 &=& 5^{x-1} &\vert & \ln{()} \cr \ln{(2)} &=& \ln{\left(5^{x-1}\right)}\cr \ln{(2)} &=& (x-1) \cdot \ln{(5)} &\vert & :\ln{(5)}\cr \dfrac{\ln{(2)}}{\ln{(5)}} &=& x-1 &\vert & +1 \cr \dfrac{\ln{(2)}}{\ln{(5)}}+1 &=& x \cr x &\approx& 1{,}43 \in\mathbb{D} & & \rightarrow \quad P_2(1{,}43 \mid 0{,}2) \end{array}$

2)
a)
$\begin{array}{rclll} f(-32) &=& f(a)= 2^{5 \cdot (-32)-3} &\approx& 8{,}55 \cdot 10^{-50} \quad \rightarrow \quad P_1(-32 \mid 8{,}55\cdot 10^{-50} ) \end{array}$

b)
$\begin{array}{rclll}8 &=& 2^{5a-3} &\vert & \log_2()\cr 3 &=& 5a-3 &\vert & +3\cr 6 &=& 5a &\vert & :5\cr a &=& \dfrac{6}{5} \in\mathbb{D} & & \rightarrow \quad P_2\left(\dfrac{6}{5} \mid 8\right)\end{array}$

3)
a)
$\begin{array}{rclll} f(-14) &=& \dfrac{1}{2} \cdot 3{,}5^{2 \cdot (-14)} &\approx& 2{,}92\cdot 10^{-16} \quad \rightarrow \quad P_1(-14 \mid 2{,}92\cdot 10^{-16}) \end{array}$

b)
$\begin{array}{rclll}\dfrac{49}{8} &=& \dfrac{1}{2} \cdot \left(\dfrac{7}{2}\right)^{2x} & \vert & \cdot 2\cr \dfrac{49}{4} &=& \left(\dfrac{7}{2}\right)^{2x} & \vert & \ln{()}\cr \ln{\left(\dfrac{49}{4}\right)} &=& \ln{\left(\left(\dfrac{7}{2}\right)^{2x}\right)}\cr \ln{\left(\left(\dfrac{7}{2}\right)^2\right)} &=& 2x \cdot \ln{\left(\dfrac{7}{2}\right)} \cr 2\ln{\left(\dfrac{7}{2}\right)} &=& 2x \cdot \ln{\left(\dfrac{7}{2}\right)} & \vert & : 2\ln \left(\dfrac{7}{2}\right)\cr x &=& 1 \in\mathbb{D} & & \rightarrow \quad P_2\left(1 \mid 6{,}125\right)\end{array}$

4)
a)
$\begin{array}{rclll} f(0{,}1) &=& \dfrac{100}{3^{0{,}1-5}} &\approx& 21.771{,}79 \quad \rightarrow \quad P_1(0{,}1 \mid 21.771{,}79) \end{array}$

b)
$\begin{array}{rclll} 8.100 &=& \dfrac{100}{3^{x-5}} &\vert & \text{Kehrwert bilden}\cr\cr \dfrac{1}{8.100} &=& \dfrac{3^{x-5}}{100} &\vert & \cdot 100\cr \dfrac{1}{81} &=& 3^{x-5}\cr 3^{-4} &=& 3^{x-5} &\vert & \log_3()\cr -4 &=& x-5 &\vert & +5\cr x &=& 1\in\mathbb{D} & & \rightarrow \quad P_2(1 \mid 8.100) \end{array}$

5)
a)
$\begin{array}{rclll} f(10) &=& e^{7 \cdot 10-15} &\approx& 5{,}83\cdot 10^{34} \quad \rightarrow \quad P_1(10 \mid 5{,}83\cdot 10^{34}) \end{array}$

b)
$\begin{array}{rclll} -15 &=& e^{7 \cdot x-15} \cr -15 &=& \dfrac{e^{7x}}{e^{15}} &\vert & \cdot e^{15}\cr -15\cdot e^{15} &=& e^{7x} &\vert & \ln() \cr \ln(-15\cdot e^{15}) &=& 7x\end{array}$

Da der Logarithmus einer negativen Zahl nicht definiert ist, hat diese Gleichung keine Lösung: Das bedeutet, dass die Funktion nirgends den Funktionswert $-15$ annimmt.

6)
a)
$\begin{array}{rclll} f\left(\dfrac{1}{11}\right) &=& -13 \cdot e^{22 \cdot \frac{1}{11}} &\approx & -96{,}06 \quad \rightarrow \quad P_1\left(\dfrac{1}{11} \mid -96{,}06 \right) \end{array}$

b)
$\begin{array}{rclll} -13 &=& -13 \cdot e^{22x} &\vert & : \left(-13\right)\cr 1 &=& e^{22x} &\vert & \ln()\cr 0 &=& 22x &\vert & : 22\cr x &=& 0 \in\mathbb{D} & & \rightarrow \quad P_2\left(0 \mid -13\right) \end{array}$

7)
a)
$\begin{array}{rclll} f(-9) &=& 10^{(-9)^2-4}-1 &=& 10^{77}-1 \quad \rightarrow \quad P_1(-9 \mid 10^{77}-1) \end{array}$

b)
$\begin{array}{rclll} 9 &=& 10^{x^2-4}-1 &\vert & +1 \cr 10 &=& 10^{x^2-4} &\vert & \log_{10}()\cr 1 &=& x^2-4 &\vert & +4\cr 5 &=& x^2 &\vert & \pm\sqrt{ }\cr\cr x_2 &=& \sqrt{5} \in\mathbb{D} & & \rightarrow \quad P_2\left(\sqrt{5} \mid 9\right) \cr x_3 &=& -\sqrt{5} \in\mathbb{D} & & \rightarrow \quad P_3\left(-\sqrt{5} \mid 9\right)\end{array}$

8)
a)
$\begin{array}{rclll} f(-0{,}5) &=& 27 \cdot e^{(-0{,}5)^3-(-0{,}5)^2} &\approx& 18{,}56 \quad \rightarrow \quad P_1(-0{,}5 \mid 18{,}56) \end{array}$

b)
$\begin{array}{crclll} & 27 &=& 27 \cdot e^{x^3-x^2} &\vert & : 27 \cr &1 &=& e^{x^3-x^2} &\vert & \ln{()} \cr & 0 &=& x^3-x^2 \cr & 0 &=& x^2(x-1) & \vert & \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & x^2 &=& 0 &\vert& \pm\sqrt{} \cr & x_1 &=& 0 \in\mathbb{D} & & \rightarrow \quad P_2(0 \mid 27) \cr\cr \text{Faktor 2:} & x-1 &=& 0 &\vert & +1 \cr & x_2 &=& 1 \in\mathbb{D} & & \rightarrow \quad P_3(1 \mid 27) \end{array}$

9)
a)
$\begin{array}{rclll} g\left(\dfrac{11}{10}\right) &=& 2^{\frac{1}{2} \cdot \left(\frac{11}{10}\right)^2-1}+1 &\approx & 1{,}76 \quad \rightarrow \quad P_1\left(\dfrac{11}{10} \mid 1{,}76 \right) \end{array}$

b)
$\begin{array}{rclll} 1 &=& 2^{\frac{1}{2} y^2-1}+1 &\vert & -1 \cr 0 &=& 2^{\frac{1}{2} y^2-1}\cr 0 &=& \dfrac{2^{\frac{1}{2} y^2}}{2} &\vert & \cdot 2\cr 0 &=& 2^{\frac{1}{2} y^2} &\vert & \log_{2}{( )}\cr \log_{2}{(0)} &=& \dfrac{1}{2} y^2\end{array}$

Da der Logarithmus von $0$ nicht definiert ist, hat diese Gleichung keine Lösung: Das bedeutet, dass die Funktion nirgends den Funktionswert $1$ annimmt.

10)
a)
$\begin{array}{rclll} f(17) &=& 1+\dfrac{2.000}{4^{17+1}} &\approx & 1{,}000000029 \quad \rightarrow \quad P_1(17 \mid 1{,}000000029) \end{array}$

b)

$\begin{array}{rclll} 32.001 &=& 1+\dfrac{2.000}{4^{x+1}} &\vert & -1 \cr\cr 32.000 &=& \dfrac{2.000}{4^{x+1}} &\vert & \text{Kehrwert bilden}\cr\cr \dfrac{1}{32.000} &=& \dfrac{4^{x+1}}{2.000} &\vert & \cdot 2.000\cr \dfrac{1}{16} &=& 4^{x+1} \cr 4^{-2} &=& 4^{x+1} &\vert & \log_{4}()\cr -2 &=& x+1 &\vert & -1\cr x &=& -3 \in\mathbb{D} & & \rightarrow \quad P_2(-3 \mid 32.001) \end{array}$

5. Aufgabe

1)
$\begin{array}{crclcl} & \mathbb{D} &=& \mathbb{R} \cr\cr & 0 &=& x e^x &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & 0 &=& x \cr\cr \text{Faktor 2:} & 0 &=& e^x \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert der zweite Faktor keine weiteren Nullstellen. Die einzige Nullstelle von $f(x)$ liegt bei $x=0$.

2)
$\begin{array}{crclcl} & \mathbb{D} &=& \mathbb{R} \cr\cr & 0 &=& 6e^x+xe^x+2e^x \cr & 0 &=& (x+8)e^x &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & 0 &=& x+8 &\vert& -8 \cr & -8 &=& x \cr\cr \text{Faktor 2:} & 0 &=& e^x \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert der zweite Faktor keine weiteren Nullstellen. Die einzige Nullstelle von $f(x)$ liegt bei $x=-8$.

3)
$\begin{array}{crclcl} & \mathbb{D} &=& \mathbb{R} \cr\cr & 0 &=& 123(x+13)10^{2x+5} &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & 0 &=& 123(x+13) &\vert& :123 \cr & 0 &=& x+13 &\vert& -13 \cr & -13 &=& x \cr\cr \text{Faktor 2:} & 0 &=& 10^{2x+5} \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert der zweite Faktor keine weiteren Nullstellen. Die einzige Nullstelle von $f(x)$ liegt bei $x=-13$.

4)
$\begin{array}{lrclcl} & \mathbb{D} &=& \mathbb{R} \cr\cr & 0 &=& 2x\left(2x^2e^{x^3+1}-9exe^{x^3}-5e^{x^3+1}\right) \cr & 0 &=& 4x^3e^{x^3+1}-18x^2e^{x^3+1}-10xe^{x^3+1} \cr & 0 &=& e^{x^3+1}\left(4x^3-18x^2-10x\right) &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & 0 &=& e^{x^3+1} \cr\cr \text{Faktor 2:} & 0 &=& 4x^3-18x^2-10x \cr & 0 &=& x\left(4x^2-18x-10\right) &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 2.1:} & 0 &=& x_1 \cr\cr \text{Faktor 2.2:} & 0 &=& 4x^2-18x-10 &\vert& :4 \cr & 0 &=& x^2-\dfrac{9}{2}x-\dfrac{5}{2} &\vert& \text{p-q-Formel} \cr\cr & x_{2,3} &=& \dfrac{9}{4} \pm \sqrt{\left(-\dfrac{9}{4}\right)^2+\dfrac{5}{2}} \cr & &=& \dfrac{9}{4} \pm \sqrt{\dfrac{121}{16}} \cr\cr & x_2 &=& \dfrac{9}{4} + \dfrac{11}{4} = 5 \cr\cr & x_3 &=& \dfrac{9}{4} - \dfrac{11}{4} = -\dfrac{1}{2} \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert der erste Faktor keine weiteren Nullstellen. Die Nullstellen von $f(x)$ liegen bei $x_1=0$, $x_2=5$ und $x_3=-\dfrac{1}{2}$.

5)
$\begin{array}{lrclcl} & \mathbb{D} &=& \mathbb{R} \cr\cr & 0 &=& (v^2+2v-2) \cdot e^{-6v} &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & 0 &=& e^{-6v} \cr\cr \text{Faktor 2:} & 0 &=& v^2+2v-2 &\vert& \text{p-q-Formel} \cr & v_{1,2} &=& -1 \pm \sqrt{1^2+2} \cr\cr & v_1 &=& -1+\sqrt{3} \approx 0{,}73 \cr & v_2 &=& -1-\sqrt{3} \approx -2{,}73 \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert der erste Faktor keine weiteren Nullstellen. Die Nullstellen von $f(v)$ liegen bei $v_1=-1+\sqrt{3}$ und $v_2=-1-\sqrt{3}$.

6)
$\begin{array}{rclcll}\mathbb{D} &=& \mathbb{R} \cr\cr 0 &=& 3^x-2 &\vert& -3^x \\-3^x &=& -2 &\vert&\cdot (-1) \\3^x &=& 2 &\vert& \log_{3}() \\x &=& \log_{3}(2)\end{array}$

Die Nullstelle von $f(x)$ liegt bei $x=\log_{3}(2)$.

7)
$\begin{array}{rclcll}\mathbb{D} &=& \mathbb{R}\setminus_{\{-\frac{1}{2}\}} \\ \\0 &=& \dfrac{e^y}{e^{2y+1}}-{e^y}^2 &\vert & +{e^y}^2 \\ \\{e^y}^2 &=& e^{y-(2y+1)} \\{e^y}^2 &=& e^{-y-1} &\vert& \ln() \\\ln\left({e^y}^2\right) &=& \ln\left(e^{-y-1}\right) \\y^2 &=& -y-1 &\vert& +y+1 \\y^2+y+1 &=& 0 &\vert &\text{p-q-Formel} \\y_{1,2} &=& -\dfrac{1}{2}\pm\sqrt{\left(\dfrac{1}{2}\right)^2-1} \\&=& -\dfrac{1}{2}\pm\sqrt{-\dfrac{3}{4}} \\\end{array}$

Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Funktion keine Nullstellen.

8)
$\begin{array}{rclcll}\mathbb{D} &=& \mathbb{R} \cr\cr 0 &=& 100^x+10^x-10 \\0 &=& (10^2)^x+10^x-10 \\0 &=& (10^x)^2+10^x-10 \\\end{array}$

Substitution: $u=10^x$
$\begin{array}{rclcll}u^2+u-10 &=& 0 &\vert& \text{p-q-Formel} \\u_{1,2} &=& -\dfrac{1}{2}\pm\sqrt{\left(\dfrac{1}{2}\right)^2+10} \\ \\&=& -\dfrac{1}{2}\pm\sqrt{\dfrac{41}{4}} \\ \\u_1 &=& -\dfrac{1}{2}+\dfrac{\sqrt{41}}{2} \approx 2{,}70 \\ \\u_2 &=& -\dfrac{1}{2}-\dfrac{\sqrt{41}}{2} \approx -3{,}70 \\ \\\end{array}$

Rücksubstitution:
$\begin{array}{rclcll}u_1 =10^{x_1} &=& -\dfrac{1}{2}+\dfrac{\sqrt{41}}{2} &\vert& \lg() \\ \\x_1 &=& \lg \left(-\dfrac{1}{2}+\dfrac{\sqrt{41}}{2}\right)\approx 0{,}4316 \\ \\u_2 =10^{x_2} &=& -\dfrac{1}{2}-\dfrac{\sqrt{41}}{2}\end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert die Rücksubstitution von $u_2$ keine weiteren Nullstellen. Die einzige Nullstelle von $f(x)$ liegt bei $x=\lg\left(-\dfrac{1}{2}+\dfrac{\sqrt{41}}{2}\right)$.

9)
$\begin{array}{rclcll}\mathbb{D} &=& \mathbb{R} \cr\cr 0 &=& -12\cdot 5^{3x}\cdot 5^{-x+1}+60 &\vert& -60 \\-60 &=& -12\cdot 5^{3x}\cdot 5^{-x+1} \\-60 &=& -12\cdot 5^{2x+1} &\vert& :(-12) \\5 &=& 5^{2x+1} &\vert& \log_{5}() \\\log_{5} \left(5\right) &=& \log_{5} \left(5^{2x+1}\right) \\1 &=& 2x+1 &\vert& -1\\0 &=& 2x &\vert& :2\\x &=& 0\end{array}$ 

Die Nullstelle von $f(x)$ liegt bei $x=0$.

10)
$\begin{array}{rclcll}\mathbb{D} &=& \mathbb{R} \cr\cr 0 &=& -2\cdot 3^x+9^x-2 \\0 &=& (3^2)^x-2\cdot 3^x-2 \\0 &=& (3^x)^2-2\cdot 3^x-2\end{array}$

Substitution: $u = 3^x$
$\begin{array}{rclcll}u^2-2u-2 &=& 0 &\vert& \text{p-q-Formel} \\u_{1,2} &=& 1\pm\sqrt{(-1)^2+2}\\&=& 1\pm\sqrt{3} \\ \\u_1 &=& 1+\sqrt{3} \approx 2{,}73 \\u_2 &=& 1-\sqrt{3} \approx -0{,}73\end{array}$

Rücksubstitution:
$\begin{array}{rclcll}u_1 = 3^x &=& 1+\sqrt{3} &\vert& \log_3() \\x_1 &=& \log_{3} (1+\sqrt{3})\approx 0{,}9148 \\ \\u_2 = 3^x &=& 1-\sqrt{3} \\\end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert die Rücksubstitution von $u_2$ keine weiteren Nullstellen. Die einzige Nullstelle von $f(x)$ liegt bei $x_1=\log_{3}\left(1+\sqrt{3}\right)$.

11)
$\begin{array}{lrclcl} & \mathbb{D} &=& \mathbb{R} \cr\cr & 0 &=& (-5z^2+35) \cdot e^{z} &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & 0 &=& e^{z} \cr\cr \text{Faktor 2:} & 0 &=& -5z^2+35 &\vert& -35 \cr & -35 &=& -5z^2 &\vert& :(-5) \cr & 7 &=& z^2 \cr\cr & z_1 &=& \sqrt{7} \cr & z_2 &=& -\sqrt{7} \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert der erste Faktor keine weiteren Nullstellen. Die Nullstellen von $f(z)$ liegen bei $z_1=\sqrt{7}$ und $z_2=-\sqrt{7}$.

12)
$\begin{array}{lrclcl} & \mathbb{D} &=& \mathbb{R} \cr\cr & 0 &=& (a^2x-3a)\cdot e^{2-ax} &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & 0 &=& e^{2-ax} \cr\cr \text{Faktor 2:} & 0 &=& a^2x-3a \cr & 0 &=& a(ax-3) &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 2.1:} & 0 &=& a_1 \cr\cr \text{Faktor 2.2:} & 0 &=& ax-3 &\vert& +3 \cr & 3 &=& ax &\vert& :x \cr & a_2 &=& \dfrac{3}{x} \end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert der erste Faktor keine weiteren Nullstellen. Die Nullstelle von $f(a)$ liegen bei $a_1=0$ und $a_2=\dfrac{3}{x}$.

Bemerkung: Bitte achten Sie darauf, dass die Variable hier $a$ und nicht $x$ ist! Das erkennt man daran, dass die Funktion $f(a)$ heißt ...
Bei der Lösung $a_2$ wird deutlich, dass der Parameter $x\neq 0$ sein muss, da wir ja durch den Parameter teilen. Das wird auch dann plausibel, wenn man sich anschaut, wie der Funktionsterm für $x=0$ aussieht, nämlich $f(a) = -3a\cdot e^{2}$. Diese Funktion ist linear, da $e^2 \approx 7{,}39$ eine Konstante ist, und lineare Funktionen können nun mal nicht mehr als eine Nullstelle haben.

13)
$\begin{array}{lrclcl} & \mathbb{D} &=& \mathbb{R} \cr\cr & 0 &=& \left(\dfrac{5}{3}y^2-\dfrac{7}{4}y+8\right) \cdot e^{-\frac{1}{2}y^2+2} &\vert& \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & 0 &=& e^{-\frac{1}{2}y^2+2} \cr\cr \text{Faktor 2:} & 0 &=& \dfrac{5}{3}y^2-\dfrac{7}{4}y+8 &\vert& \cdot \dfrac{3}{5} \cr\cr & 0 &=& y^2-\dfrac{21}{20}y+\dfrac{24}{5} &\vert& \text{p-q-Formel} \cr\cr & y_{1,2} &=& \dfrac{21}{40} \pm \sqrt{\left(-\dfrac{21}{40}\right)^2-\dfrac{24}{5}} \cr & y_{1,2} &=& \dfrac{21}{40} \pm \sqrt{-\dfrac{7.239}{1.600}} \end{array}$

Da Potenzen niemals negativ oder $0$ sein können und aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat $g(y)$ keine Nullstellen.

14)
$\begin{array}{rclcll}\mathbb{D} &=& \mathbb{R} \cr\cr0 &=& \dfrac{e^{x^2}\cdot e^{-2}}{e^x}-1 &\vert& +1 \\1 &=& \dfrac{e^{x^2}\cdot e^{-2}}{e^x} \\1 &=& e^{x^2-2}\cdot e^{-x} \\1 &=& e^{x^2-2-x} &\vert& \ln()\\\ln (1) &=& \ln \left(e^{x^2-2-x}\right) \\0 &=& x^2-x-2 &\vert&\text{p-q-Formel} \\x_{1,2} &=& \dfrac{1}{2}\pm\sqrt{\left(-\dfrac{1}{2}\right)^2+2} \\\\&=& \dfrac{1}{2}\pm\sqrt{\dfrac{9}{4}} \\\\x_1 &=& \dfrac{1}{2}+\dfrac{3}{2} = 2 \\x_2 &=& \dfrac{1}{2}-\dfrac{3}{2} = -1\end{array}$

Die Nullstellen von $f(x)$ liegen bei $x_1=2$ und bei $x_2=-1$.

15)
$\begin{array}{rclcll}\mathbb{D} &=& \mathbb{R} \\ \\0 &=& \dfrac{8}{2^{x^2}}-2^{-2x} &\vert& +2^{-2x} \\ \\2^{-2x} &=& \dfrac{8}{2^{x^2}} &\vert& \cdot 2^{x^2} \\2^{-2x}\cdot 2^{x^2} &=& 8 \\2^{x^2-2x} &=& 2^3 &\vert& \log_2() \\x^2-2x &=& 3 &\vert& -3 \\x^2-2x-3 &=& 0 &\vert& \text{p-q-Formel} \\x_{1,2} &=& 1\pm\sqrt{(-1)^2+3} \\&=& 1\pm\sqrt{4} \\ \\x_1 &=& 1-2=-1 \\x_2 &=& 1+2=3\end{array}$

Die Nullstellen von $f(x)$ liegen bei $x_1=-1$ und bei $x_2=3$.

Bemerkung: Die Multiplikation mit $2^{x^2}$ ist hier ohne Einschränkungen möglich, weil $2^{x^2}$ immer größer als $0$ ist. Eine Multiplikation mit $0$ kann also nicht passieren.

16)
$\begin{array}{rclll}\mathbb{D} &=& \mathbb{R} \cr\cr a\cdot4^a-2\dfrac{1}{4^{-a}}+a^2\cdot 4^a &=& 0 \\a^2\cdot 4^a+a\cdot4^a-2\cdot 4^a &=& 0 &\vert & :4^a\\a^2+a-2 &=& 0 &\vert & \text{p-q-Formel}\\a_{1,2} &=& -\dfrac{1}{2}\pm\sqrt{\left(\dfrac{1}{2}\right)^2+2}\\a_{1,2} &=& -\dfrac{1}{2}\pm\sqrt{\dfrac{9}{4}}\\\\a_1 &=& -\dfrac{1}{2}+\dfrac{3}{2} = 1\\a_2 &=& -\dfrac{1}{2}-\dfrac{3}{2} = -2\end{array}$

Die Nullstellen von $f(a)$ liegen bei $a_1=1$ und bei $a_2=-2$.

Bemerkung: Die Division durch $4^{a}$ ist hier ohne Einschränkungen möglich, weil $4^{a}$ immer größer als $0$ ist. Eine Division durch $0$ kann also nicht passieren.

17) 
$\begin{array}{rclll}\mathbb{D} &=& \mathbb{R} \cr\cr t\cdot e^{t-1}+e^t-e^{t-1} &=& 0 \\e^{t-1}\left(t+e^1-1\right) &=& 0 &\vert & :e^{t-1} \\t+e-1 &=& 0 &\vert& -e+1\\t &=& 1-e\approx -1{,}7183\end{array}$

Die Nullstelle von $g(t)$ liegt bei $t=1-e$.

Bemerkung: Die Division durch $e^{t-1}$ ist hier ohne Einschränkungen möglich, weil $e^{t-1}$ immer größer als $0$ ist. Eine Division durch $0$ kann also nicht passieren.

18)
$\begin{array}{crclll}& \mathbb{D} &=& \mathbb{R}\setminus_{\{-1\}} \\\\& \dfrac{3}{\left(x+1\right)^2}\cdot\left(e^{\frac{4}{5}x+3}-3\right) &=& 0 \\\\\text{Faktor 1:} & \dfrac{3}{\left(x+1\right)^2} &=& 0 &\vert& \cdot \left(x+1\right)^2 \\& 3 &=& 0 \\\\\text{Faktor 2:} & e^{\frac{4}{5}x+3}-3 &=& 0 &\vert & +3 \\& e^{\frac{4}{5}x+3} &=& 3 &\vert & \ln() \\& \dfrac{4}{5}x+3 &=& \ln(3) &\vert & -3\\& \dfrac{4}{5}x &=& \ln(3) -3 &\vert & :\dfrac{4}{5}\\& x &=& \dfrac{5}{4}\left(\ln(3) -3\right) \approx -2{,}38\end{array}$

Da der erste Faktor zu einem Widerspruch führt, liefert er keine weiteren Nullstellen. Die einzige Nullstelle von $f(x)$ liegt bei $x=\dfrac{5}{4}\left(\ln(3) -3\right)$.

Bemerkung: Die Multiplikation mit $(x+1)^2$ ist hier ohne Einschränkungen möglich, weil $x=-1 \not\in \mathbb{D}$. Eine Multiplikation mit $0$ kann also nicht passieren.

19) 
$\begin{array}{lrclll}& \mathbb{D} &=& \mathbb{R} \\\\& 3e^{-\frac{2}{3}y+5}\cdot\left(y^3+3y^2-4y\right) &=& 0 \\\\\text{Faktor 1:} & 3e^{-\frac{2}{3}y+5} &= & 0 &\vert& :3 \\& e^{-\frac{2}{3}y+5} &= & 0 \\\\\text{Faktor 2:} & y^3+3y^2-4y &=& 0 \\& y\left(y^2+3y-4\right) &=& 0 \\\text{Faktor 2.1:} & y_1 &=& 0 \\\\\text{Faktor 2.2:} & y^2+3y-4 &=& 0 &\vert& \text{p-q-Formel} \\& y_{2,3} &=& -\dfrac{3}{2}\pm\sqrt{\left(\dfrac{3}{2}\right)^2+4}\\& y_{2,3} &=& -\dfrac{3}{2}\pm\sqrt{\dfrac{25}{4}}\\\\& y_2 &=& -\dfrac{3}{2}+\dfrac{5}{2} = 1\\& y_3 &=& -\dfrac{3}{2}-\dfrac{5}{2} = -4\end{array}$

Da Potenzen niemals negativ oder $0$ sein können, liefert der erste Faktor keine weiteren Nullstellen. Die Nullstellen von $f(y)$ liegen bei $y_1=0$, $y_2=1$ und bei $y_3=-4$.

20)
$\begin{array}{rclll}\mathbb{D} &=& \mathbb{R} \\\\\dfrac{e^{13x}-64}{201e^{x+52}} &=& 0 &\vert& \cdot 201e^{x+52} \\\\e^{13x}-64 &=& 0 &\vert & +64\\e^{13x} &=& 64 &\vert & \ln() \\13x &=& \ln(64) &\vert &:13 \\x &=& \dfrac{\ln(64)}{13} \approx 0{,}32\end{array}$

Die Nullstelle von $f(x)$ liegt bei $x=\dfrac{\ln(64)}{13}$.

Bemerkung: Die Multiplikation mit $201e^{x+52}$ ist hier ohne Einschränkungen möglich, weil $201e^{x+52}$ immer größer als $0$ ist. Eine Multiplikation mit $0$ kann also nicht passieren.