Lernmodul Mathematik
Dieses Kapitel enthält die folgenden Themen:
15.2 Wurzelgleichungen und -funktionen - Erklärungen
Nachdem wir uns im Kapitel Potenzen, Wurzeln, Logarithmen angeschaut haben, wofür Wurzeln gut sind und wie sie funktionieren, ist es wohl nicht sehr überraschend, dass sie auch Teil von Gleichungen und Funktionen sein können. Benötigt werden Wurzeln in Gleichungen und Funktionen beispielsweise, wenn der Satz des Pythagoras irgendwo "mitspielt" (z. B. bei der Diagonalen eines Quadrates in Abhängigkeit der Seitenlänge), aber auch in der Statistik, wo Wurzeln in der Formel für die Standardabweichung enthalten sind.
Wer sich (noch) nicht mit den Rechenregeln für Wurzeln vertraut gemacht hat, sollte dies nun nachholen. Auch mit Potenzen und binomischen Formeln sollten Sie sich auskennen. Wir werden diese Rechenregeln und -gesetze im nun folgenden Kapitel brauchen.
Definition
Definition einer Wurzelgleichung: Wurzelgleichungen sind Gleichungen, bei denen die Variable im Radikanden von Wurzeln steht.
Definition einer Wurzelfunktion: Wurzelfunktionen sind Funktionen, bei denen die Variable im Radikanden von Wurzeln steht.
Es ist egal, ob es sich um eine zweite, dritte, vierte etc. Wurzel handelt. Natürlich müssen die Wurzelterme nicht alleine in der Gleichung/Funktion stehen, sondern dürfen mit allem, was wir bislang in diesem Lernmodul kennengelernt haben, z. B. mit Brüchen, kombiniert werden.
Definitionsbereich: Auch bei dieser Art von Gleichung/Funktion ist es wichtig, sich Gedanken zum Definitionsbereich zu machen:
- Fall: Bei geraden Wurzelexponenten darf der Radikand im Bereich der reellen Zahlen nicht negativ sein. Wir müssen also prüfen, für welche Variablenwerte das passiert, und den Definitionsbereich so "zuschneiden", dass nur passende Werte enthalten sind. Dafür müssen Ungleichungen gelöst werden.
- Fall: Bei ungeraden Wurzelexponenten dürfen auch negative Zahlen im Radikand stehen, denn es gilt ja:
für ungerade
.
Wurzelgleichungen
Wie immer einige einleitende Beispiele:
mit
mit
mit
Achtung: Diese Gleichung sieht nur aus wie eine Wurzelgleichung. Man kann sie leicht vereinfachen, indem man die Wurzel ausrechnet. Dann steht da nur noch eine lineare Gleichung, nämlich.
Lösungsweg
Grundsätzliches Vorgehen bei Wurzelgleichungen ist, dass man zunächst versucht, die Wurzel allein auf eine Seite der Gleichung zu bringen. Mathematisch sagt man: Die Wurzel wird auf einer Seite der Gleichung isoliert. Potenziert man anschließend die Gleichung mit dem Wurzelexponenten, bleibt von der isolierten Wurzel nur der Radikand stehen. Je nachdem, woraus der Radikand besteht, bleibt danach in vielen Fällen nur eine lineare oder quadratische Gleichung übrig. Damit haben wir wieder ein neues Problem auf etwas zurückgeführt, von dem wir schon wissen, wie man damit umgeht.
Wichtig zu wissen ist noch, dass beim Lösen von Wurzelgleichungen die Probe zwingend zum Lösungsweg dazugehört. Durch den eingeschränkten Definitionsbereich kann es nämlich passieren, dass sogenannte Scheinlösungen entstehen. Dazu weiter unten mehr ...
Schauen wir uns ein paar Beispiele an:
Beispiel 1:
Betrachten wir die Gleichung .
Bestimmung des Definitionsbereichs:
Da Wurzeln aus negativen Zahlen dann erlaubt sind, wenn der Wurzelexponent ungerade ist, gibt es hier keine Einschränkungen: Der Definitionsbereich ist also .
Lösung der Gleichung:
Probe:
Für ergibt sich eine wahre Aussage:
Zur 1. Zeile: Wir subtrahieren , um den Wurzelterm auf der linken Seite der Gleichung zu isolieren.
Zur 2. Zeile: Die gesamte Gleichung wird mit potenziert, um die Wurzel aufzuheben. Wichtig: Solche Umformungen müssen immer auf beiden Seiten der Gleichung durchgeführt werden und auf die gesamte Gleichungsseite angewendet werden. Wie wir schon bei linearen Gleichungen und anderen Gleichungstypen gesehen haben, führt es zu falschen Werten, wenn Umformungen nur auf einige Bestandteile der Gleichung angewendet werden.
Ab der 3. Zeile: Resultat ist eine lineare Gleichung, die man löst wie jede andere lineare Gleichung auch.
Zur Probe: Die Probe für den berechneten Wert geht auf. Somit ist Lösung der Gleichung.
Sie sehen, dass das Lösen von Wurzelgleichungen gar nicht so kompliziert sein muss. Durch das Potenzieren entsteht eine Gleichung, die sich mit bereits bekannten Verfahren lösen lässt. So etwas mag man in der Mathematik immer gerne ...
Bei den Lösungsstrategien für Wurzelgleichungen sind zwei Aspekte besonders wichtig:
- Der Wurzelterm muss auf einer Seite der Gleichung isoliert werden.
- Wenn vor dem Quadrieren auf einer Seite der Gleichung eine Summe/Differenz steht, muss die binomische Formel verwendet werden.
Schauen wir uns an, was passiert, wenn man das nicht tut ...
Beispiel 2:
Betrachten wir die Gleichung .
Bestimmung des Definitionsbereichs:
Da der Wurzelexponent gerade ist (), muss der Radikand größer oder gleich
sein.
Der Definitionsbereich ist also .
Zunächst die korrekte Rechnung mit Probe:
Probe:
Für ergibt sich eine wahre Aussage:
Würde man den Wurzelterm nicht isolieren, wäre die Rechnung zwar grundsätzlich richtig, aber nicht zielführend:
Das ist prinzipiell nicht falsch: Die Gleichung hat die gleiche Lösung wie die ursprüngliche Gleichung
. Dass es uns auf dem Weg zur Lösung nicht weiterbringt, wenn die Gleichung nach jeder Umformung komplizierter ist als vorher, ist aber wohl auch einleuchtend. Fazit: Damit die Gleichung einfacher wird und wir der Lösung näherkommen, muss der Wurzelterm auf einer Seite der Gleichung isoliert werden.
Schlimmer als das fehlende Isolieren des Wurzelterms ist aber, wenn man beim Quadrieren einer Summe keine binomische Formel anwendet. Dann wird das Ergebnis wirklich falsch. Schauen wir uns an unserer Beispielgleichung an, was passiert, wenn man fälschlicherweise
zu
umformen würde:
Probe:
Das ist eine falsche Aussage. Die Probe geht in diesem Fall also nicht auf. Das bedeutet ist keine Lösung unserer Gleichung. Letztendlich überrascht das nicht, da wir ja gleich zu Beginn eine fehlerhafte Umformung durchgeführt haben. Wir erhalten also eine zusätzliche Bestätigung, dass die binomische Formel zu Beginn der Rechnung wirklich wichtig gewesen wäre. In diesem Beispiel hätte man das Problem natürlich umgehen können, indem man den Wurzelterm auf der linken Seite der Gleichung isoliert.
Beispiel 3:
Wenn mehrere Wurzelterme in einer Gleichung und/oder zusätzlich Terme ohne Wurzel enthalten sind, muss man die Schritte aus Beispiel 1 ggf. wiederholen. Um dies deutlich zu machen, betrachten wir die Gleichung .
Bestimmung des Definitionsbereichs:
Da beide Wurzelexponenten gerade sind, müssen beide Radikanden größer oder gleich sein.
linker Radikand:
rechter Radikand:
Für die abschließende Ermittlung des Definitionsbereichs bekommen wir also zwei Bedingungen: (für den linken Radikanden) und
(für den rechten Radikanden). Da beide Radikanden Teil der Gleichung sind, müssen natürlich auch beide Bedingungen erfüllt sein. Dies müssen wir nun prüfen:
- x-Werte kleiner als
erfüllen keine Bedingung.
- x-Werte, die größer gleich
, aber kleiner als
sind, erfüllen nur die erste Bedingung.
- Nur x-Werte größer oder gleich
erfüllen beide Bedingungen.
Der Definitionsbereich ist also .
Lösung der Gleichung:
Probe:
Für :
Für :
Nur für ergibt sich eine wahre Aussage:
Zur 1. Zeile: Zunächst fasst man die Gleichung so weit wie möglich zusammen. Je weniger einzelne Terme, desto einfacher ...
Zur 2. Zeile: Nun wird die Gleichung quadriert. Das hilft aber diesmal nur teilweise, weil nur eine der Wurzeln isoliert werden kann. Die ist ja auch noch da und steht auf der linken Gleichungsseite gemeinsam mit einem Wurzelterm.
Zur 3. Zeile: Diese Zeile müsste man grundsätzlich nicht hinschreiben. Man sieht hier aber gut, worauf beim Quadrieren geachtet werden muss: In der Klammer auf der linken Seite steht nämlich eine Differenz. Das heißt, dieses Quadrat kann nur mithilfe der 2. binomischen Formel (oder mit dem Distributivgesetz) aufgelöst werden. Das ist wichtig! Wir hatten uns oben bei Beispiel 2 und im Kapitel Potenzen, Wurzeln, Logarithmen ja angeschaut, was passiert, wenn man z. B. den mittleren Term nicht berücksichtigt. Genau der gleiche Fehler passiert hier auch.
Das ist ebenfalls eine Erklärung, warum es sinnvoll ist, die Wurzel vor dem Quadrieren auf einer Seite der Gleichung zu isolieren, wenn es möglich ist. Wenn die Wurzel nämlich alleine auf einer Seite der Gleichung steht, können wir ganz beruhigt quadrieren, weil hier keine Kombination von Potenz-, Punkt- und Strichrechnung auftritt.
Zur 4. Zeile: Da der mittlere Term der binomischen Formel ist, in diesem Fall also
, bleibt eine Wurzel weiterhin bestehen. Gut ist, dass dies nun die einzige Wurzel ist.
Zur 5. und 6. Zeile: Die verbleibende Wurzel muss nun wieder durch die üblichen Umformungen isoliert werden.
Zur 7. Zeile: Nun befindet sich die Wurzel allein auf einer Seite, und es kann ohne Probleme quadriert werden. Auf der rechten Seite muss auf die binomische Formel geachtet werden. Alle Wurzeln sind nach dieser Umformung verschwunden.
Ab der 8. Zeile: Es bleibt eine quadratische Gleichung ohne konstanten Term übrig. Daher kann ausgeklammert und anschließend der Satz vom Nullprodukt angewendet werden.
Zur Probe: Bei dieser Gleichung liefert nur eine wahre Aussage. Bei
geht die Probe nicht auf (
ist ja offensichtlich nicht richtig). Die einzige Lösung ist somit
.
Nach Abschluss der Rechnung: Prüfung auf Scheinlösungen!
Dass im dritten Beispiel die Probe für nicht aufgeht, obwohl wir völlig richtig gerechnet haben, ist bei Wurzelgleichungen (leider) durchaus typisch. Beim Lösen von Wurzelgleichungen können nämlich Scheinlösungen entstehen. Bei Bruchgleichungen hatten wir ja auch schon gesehen, dass in der Rechnung Werte entstehen können, die die Gleichung nur scheinbar lösen.
Bei Wurzelgleichungen ist die Ursache dafür, dass Quadrieren keine Äquivalenzumformung ist: Quadrieren wir die Gleichung , erhalten wir
. Das sieht erst mal unproblematisch aus, allerdings haben wir eine Lösung hinzubekommen:
löst die neue Gleichung ja auch ... Die Lösungsmengen der ursprünglichen und der neuen Gleichung sind also nicht identisch. Da man beim Lösen von Wurzelgleichungen kaum um das Quadrieren (oder allgemein das Potenzieren) herumkommt, besteht immer die Gefahr, dass solche Scheinlösungen entstehen. Um diese zu finden, muss bei Wurzelgleichungen also immer eine Probe durchgeführt werden. Bei Scheinlösungen geht die Probe nämlich nicht auf, sodass man Lösungen von Scheinlösungen unterscheiden und dann die Scheinlösungen aus der Lösungsmenge ausschließen kann.
Um noch ein bisschen präziser zu sein: Das Problem tritt dann auf, wenn der Wurzelexponent gerade ist und wir daher auf dem Lösungsweg mit einer geraden Zahl potenzieren müssen. Es schadet aber nicht, auch bei Wurzelgleichungen mit ungeraden Wurzelexponenten eine Probe durchzuführen. Lieber eine Probe zu viel, als eine zu wenig ...
Wurzelfunktionen
Auch den Verlauf und die Eigenschaften von Wurzelfunktionen wollen wir uns anhand einiger Beispiele anschauen. Wie schon bei den gebrochen rationalen Funktionen unterscheiden wir hier zwei einfache Fälle und einen komplexeren Fall.
1. Fall
Der Radikand besteht nur aus der Variablen und der Wurzelexponent ist gerade. Wir betrachten also nun Funktionen dieser Form , wobei
eine gerade Zahl ist. Hier ist der Definitionsbereich
, da aus negativen Zahlen ja keine Wurzeln gezogen werden können, wenn der Wurzelexponent gerade ist. Hier zwei Beispiele:
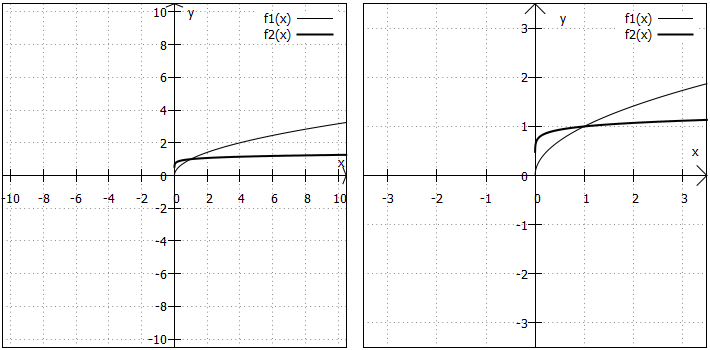
Wertebereich: Der Wertebereich dieser Funktionen umfasst nur die nichtnegativen reellen Zahlen, da Wurzeln mit geraden Wurzelexponenten grundsätzlich so definiert sind, dass keine negativen Ergebnisse entstehen können. Das ist dann natürlich auch hier so.
Randverhalten: Am unteren Rand vom Definitionsbereich können wir den Funktionswert direkt ausrechnen, weil ja Teil des Intervalls ist:
bei allen Funktionen, die wir hier gerade betrachten. Für sehr große x-Werte werden die Funktionswerte immer größer. Wurzelfunktionen wachsen zwar langsamer als alle Polynomfunktionen, aber schneller als Logarithmusfunktionen.
Symmetrie: Aufgrund des einseitig eingeschränkten Definitionsbereichs können die Graphen von Wurzelfunktionen nicht symmetrisch sein.
"Besondere Punkte": Die hier betrachteten Funktionen haben eine Nullstelle bei , aber keine Extrempunkte, Wendepunkte und Polstellen.
Weitere Besonderheiten: Diese einfachen Wurzelfunktionen verlaufen alle durch den Punkt . Das liegt daran, dass Wurzeln die Antwort auf die Frage "Welche Zahl ergibt
, wenn man sie
-mal mit sich selbst multipliziert?" geben - und egal, wie oft man die
mit sich selbst multipliziert, das Ergebnis ist immer
.
2. Fall
Der Radikand besteht nur aus der Variablen und der Wurzelexponent ist ungerade. Wir betrachten hier also Funktionen dieser Form , wobei
eine ungerade Zahl ist und zwar konkret folgende Beispiele:
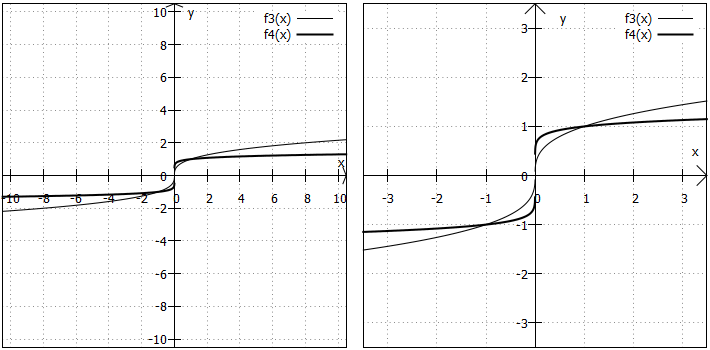
Bemerkung: In der Grafik sieht es ein bisschen so aus, als wäre der Graph bei unterbrochen. Das ist aber nicht so, sondern liegt nur an dem etwas unpräzisen Plot ...
Wertebereich: Der Wertebereich umfasst alle reellen Zahlen.
Randverhalten: Für sehr kleine x-Werte werden die Funktionswerte immer kleiner; für sehr große x-Werte immer größer. Dass Wurzelfunktionen langsamer als Polynom- aber schneller als Logarithmusfunktionen wachsen, ist hier genauso.
Symmetrie: In diesem Fall sind die Graphen von Wurzelfunktionen punktsymmetrisch zum Koordinatenursprung.
"Besondere Punkte": Die nun betrachteten Funktionen haben ebenfalls eine Nullstelle bei , aber keine Extrempunkte, Wendepunkte und Polstellen.
Weitere Besonderheiten: Im zweiten Fall verlaufen alle Funktionen durch die Punkte und
. Für den Punkt
hatten wir oben schon geklärt, warum das so ist. Für
können wir nachrechnen:
, da
ungerade ist
3. Fall
Was kann man sonst noch so mit Wurzelfunktionen machen? Natürlich geht mit Wurzelfunktionen noch viel mehr, abhängig davon was man in den Radikanden steckt und was sonst so im Funktionsterm passiert. Schauen wir uns dazu die folgenden Funktionen an:
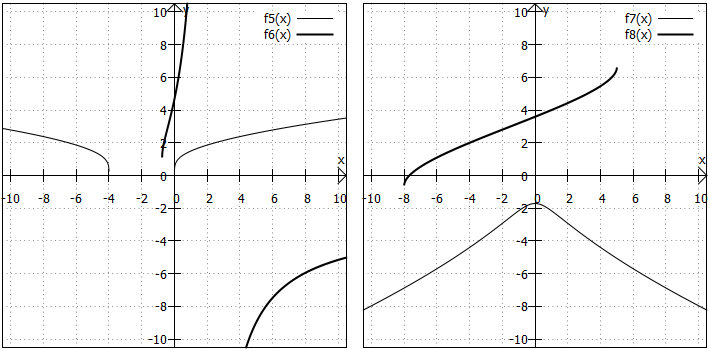
Wie Sie sehen, kann man bei Wurzelfunktionen, die über die beiden einfachen Fälle hinausgehen, keine allgemeinen Aussagen über den Verlauf und besondere Punkte der Graphen treffen.
Wertebereich: Der Wertebereich kann nur ein verhältnismäßig kleines Intervall umfassen (z. B. bei :
) oder (zumindest einseitig) unbeschränkt sein, wie bei
und
. Bei
hat der Wertebereich sogar eine "Lücke", ist aber nach oben und unten unbeschränkt.
Das ist ganz ähnlich zum Definitionsbereich.
Randverhalten: Mal werden die Funktionswerte an den Rändern des Definitionsbereichs beliebig groß oder beliebig klein. Mal können sie - wie bei - einfach ausgerechnet werden (kleinster Wert:
, größter Wert:
).
Symmetrie: Nachdem wir in den oberen Fällen gesehen haben, dass einfache Wurzelfunktionen nicht symmetrisch bzw. punktsymmetrisch sind, sind bei diesen Beispielen zwei achsensymmetrische Graphen dabei: ist achsensymmetrisch zu einer senkrechten Gerade durch
und
ist achsensymmetrisch zur y-Achse.
"Besondere Punkte":
In der Grafik wird deutlich, dass nicht jede dieser komplexeren Funktionen eine Nullstelle hat (siehe z. B. und
). Allerdings ist es schon so, dass mehr "besondere Punkte" auftreten können, je komplexer der Funktionsterm ist:
Beispielsweise hat einen Extrempunkt
. Um genau zu sein, ist es ein Hochpunkt.
Die Funktion hat einen Wendepunkt bei
. Dort ändert sich die Krümmung von einer Rechtskurve zu einer Linkskurve.
hat eine Polstelle bei
, weil dort der Nenner eine Nullstelle hat, die nicht gleichzeitig Nullstelle des Zählers ist.