SOS Mathematik
Dieses Kapitel enthält die folgenden Themen:
- Trigonometrie am Dreieck
- Die trigonometrischen Funktionen
- Die Additionstheoreme
- Der "trigonometrische Pythagoras"
- Die invers trigonometrischen Funktionen
21.2 Trigonometrie - Erklärungen
Die Trigonometrie ist insofern ein spannender mathematischer Bereich, weil ihre Vorstufen schon in den Antike bekannt waren. Benötigt wurden trigonometrische Berechnungen damals vor allem in der Astronomie und für Landvermessungen. Auch für die Navigation in der Seefahrt ist die Trigonometrie schon sehr lange wichtig. Es gibt also ganz praktische Anwendungsfälle.
Wichtig: Bei allen Aufgaben im Bereich der Trigonometrie ist darauf zu achten, ob die Winkel im Grad- oder im Bogenmaß gegeben sind und ob der Taschenrechner, der bei diesen Aufgaben durchaus sinnvoll ist, entsprechend eingestellt ist. Viele Taschenrechner zeigen bei der Einstellung Gradmaß ein "D" oder "DEG" und bei der Einstellung Bogenmaß ein "R" oder "RAD" (für Radiant) am oberen Rand des Displays.
Auch anhand der Ergebnisse ist der Unterschied zu erkennen: Ist der Taschenrechner auf Gradmaß eingestellt, erhält man bzw.
. Ist umgekehrt der Taschenrechner auf Bogenmaß eingestellt, erhält man
bzw.
. Alle diese "Ergebnisse" sind FALSCH!
Korrekt ist und damit
bzw.
und damit
Trigonometrie am Dreieck
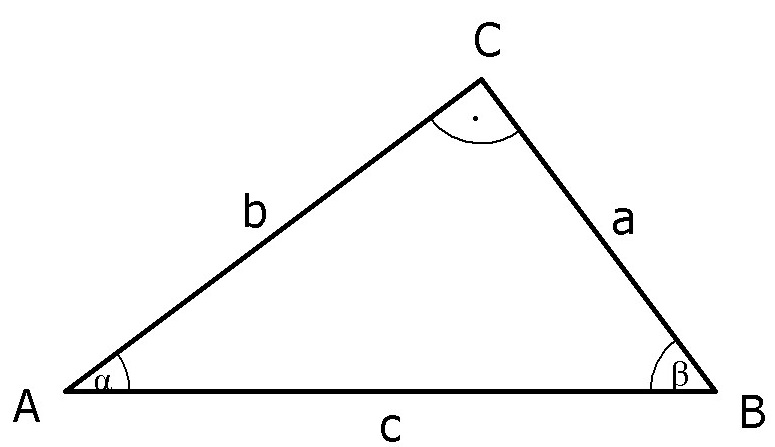 |
Im rechtwinkligen Dreieck gilt (alle Bezeichnungen entsprechend der oberen Zeichnung):
| Sinus: | und | ||||
| Kosinus: | und | ||||
| Tangens: | und | ||||
| Kotangens: | und |
Die Ankathete zu einem Winkel ist die Kathete, die an diesen Winkel angrenzt, wohingegen die Gegenkathete eines Winkels dem Winkel gegenüberliegt. Die Hypotenuse liegt immer dem rechten Winkel gegenüber.
Bemerkung 1: Ganz wichtig: Alle diese Berechnungen funktionieren wirklich nur am rechtwinkligen Dreieck. Für Dreiecke ohne rechten Winkel gibt es Verallgemeinerungen, die dann Sinussatz und Kosinussatz heißen.
Bemerkung 2: Es gilt für alle :
und
Bemerkung 3: Der Kotangens wird selten verwendet, weil für alle gilt:
. Er wird also nicht wirklich gebraucht.
Zur Schreibweise:
- Bei all diesen Funktionen können die Klammern weggelassen werden, wenn keine Verwechslungsgefahr besteht. Man schreibt dann beispielsweise:
.
- Dringend notwendig sind die Klammern aber dann, wenn Verwechslungen auftreten können. Beispielsweise könnte
sowohl
als auch
meinen.
Trigonometrische Funktionen
Begreift man den Winkel als unabhängige Variable, d. h. fasst man als Winkel im Bogenmaß auf, entstehen aus diesen Rechenvorschriften Funktionen, die trigonometrische Funktionen oder Winkelfunktionen genannt werden.
Dann schreibt man: mit dem Definitionsbereich
und dem Wertebereich
mit
und
mit
und
mit
und
Bemerkung: Die Lücken in den Definitionsbereichen von Tangens und Kotangens erklären sich aus der Bemerkung 1 von oben: Da sich der Tangens als Quotient von Sinus und Kosinus darstellen lässt, kann er an den Stellen, wo der Nenner wird, nicht definiert sein. Der Kosinus hat eine Nullstelle bei
und dann jeweils im Abstand von
in beide Richtungen weitere, also z. B. bei
oder bei
. Das lässt sich mathematisch ausdrücken mit
mit
(
ist hierbei die Menge der ganzen Zahlen).
Analog beim Kotangens.
Die trigonometrischen Funktionen sind periodische Funktionen, d. h. ihre Funktionswerte wiederholen sich in regelmäßigen Abständen. Der kleinste Abstand dieser Wiederholung, Periode genannt, beträgt bei der Sinus- und der Kosinusfunktion , bei der Tangens- und der Kotangensfunktion
In der folgenden Grafik sind die Graphen der Sinus- (dünne Linie) und der Kosinusfunktion (fette Linie) dargestellt:

In der nun folgenden Grafik sind die Graphen der Tangens- (dünne Linie) und der Kotangensfunktion (fette Linie) dargestellt:
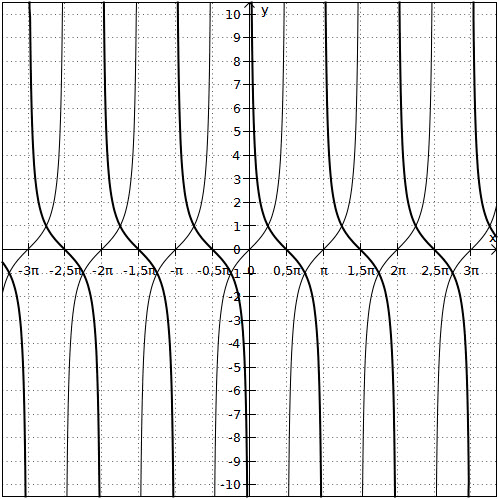
Additionstheoreme
Noch eine ganz wichtige Sache im Zusammenhang mit trigonometrischen Funktionen:
Die Summe zweier Sinuswerte ist nicht das Gleiche wie die Summe der Winkel, von der dann der Sinus berechnet wird! Dies kann man sich beispielsweise anhand der folgenden Rechnung klarmachen: kann schon deshalb nicht das Gleiche sein wie oben, weil der Sinus ja maximal den Wert
annehmen kann.
Natürlich kann man aber auch mit Summen in Sinus- bzw. Kosinusfunktionen rechnen. Dafür gibt es die sogenannten Additionstheoreme, nämlich
für alle :
und noch einige weitere ...
Der "trigonometrische Pythagoras"
Eine ganz wichtige Formel ...
Es gilt für alle :
Achtung: Mit ist
gemeint und nicht
.
Inverse trigonometrische Funktionen
Die Berechnung von Winkel kann im rechtwinkligen Dreieck mithilfe der inversen trigonometrischen Funktionen geschehen. Weil die Winkel hier üblicherweise im Bogenmaß verwendet werden und "Arkus" das lateinische Worte für "Bogen" ist, werden diese Funktionen auch Arkusfunktionen genannt. Beispielsweise liefert die Arkussinusfunktion zu einem gegebenen Wert (der, wie wir unten sehen werden, zwischen
und
liegen muss) einen Winkel
, für den
gilt. Die Bezeichnungen, die im Folgenden verwendet werden, beziehen sich alle wieder auf die Zeichnung am Anfang der Seite.
| Arkussinus: | und | ||||
| Arkuskosinus: | und | ||||
| Arkustangens: | und |
Auf dem Taschenrechner steht statt meist
, statt
und statt
. Bitte beachten Sie, dass damit nicht der Kehrwert gemeint ist!
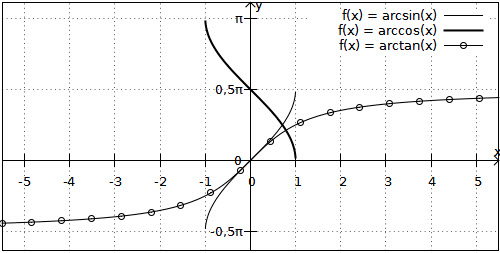
Auch wenn in diesem Lernmodul vor allem die Winkelberechnung als Anwendungsfall der Arkusfunktionen betrachtet wird, sind sie natürlich für viele andere Bereiche auch nützlich bzw. notwendig. Wenigstens die Graphen der Arkusfunktionen sollen nicht fehlen: mit dem Definitionsbereich
und dem Wertebereich
als Umkehrfunktion zu
mit
und
mit
und
als Umkehrfunktion zu
mit
und
mit
und
als Umkehrfunktion zu
mit
und
Bemerkung 1: Bitte beachten Sie, dass der Arkussinus und der Arkuskosinus nicht für alle reellen Zahlen definiert sind, sondern nur auf dem Intervall . Warum ist das so? Umkehrfunktionen "beantworten" grundsätzlich die Frage: "Wie lautete das Argument der Funktion, wenn wir xy als Ergebnis erhalten haben?" Die Umkehrfunktion bekommt also das Ergebnis der Ursprungsfunktion als Argument und liefert das Argument der Ursprungsfunktion zurück. Nun können Sinus und Kosinus ja bekanntlich nur Werte zwischen
und
annehmen. Fragen der Art "Wie lautete das Argument der Sinusfunktion, wenn wir als Ergebnis
erhalten haben?" sind also sinnlos.
Bemerkung 2: Manchmal müssen beim Bilden von Umkehrfunktionen die Definitionsbereiche der ursprünglichen Funktionen eingeschränkt werden, so auch hier. Warum das? Wegen der Periodizität der trigonometrischen Funktionen hätte z. B. die Frage "Wie lautete das Argument der Sinusfunktion, wenn der Funktionswert ist?" (also genau die Frage, die
"beantworten" möchte) nicht nur die Antwort
, sondern auch
,
,
und unendlich viele andere Werte. Ließe man also die gesamten reellen Zahlen als Definitionsbereich zu, gäbe es keine eindeutige Antwort. Das ist ein Widerspruch zur Funktionsdefinition, die eine eindeutige Zuordnung der Werte verlangt. Man löst das Problem, indem man die Definitionsbereiche so einschränkt, dass jeder Funktionswert genau einmal enthalten ist. Das ist beim Sinus für
; beim Kosinus für
und beim Tangens für
der Fall. Da aus Bemerkung 1 auch folgt, dass die Wertebereiche der Umkehrfunktionen den Definitionsbereichen der ursprünglichen Funktionen entsprechen, kennen wir somit die Wertebereiche der Arkusfunktionen.
Animierte Grafik:
Sinus und Cosinus am Einheitskreis.gif (525 KB)