Übersicht:

18.1 Betragsgleichungen und -funktionen - Aufgaben

1. Aufgabe

Wie verlaufen die Graphen der folgenden Funktionen? Welche Eigenschaften und "speziellen Punkte" haben sie?
Geben Sie zudem die Definitionsbereiche an!

Hinweis: Der erste Teil der Aufgabe ist so gemeint, dass aus dem Funktionsterm Erkenntnisse über der Verlauf des Graphen abgeleitet werden sollen. Die konkreten Funktionswerte und Verläufe der Graphen interessieren hier erst im zweiten Schritt.

1) $f(x) = x^\frac{1}{2}+4$		11) $f(x) = \dfrac{1}{\vert x\vert+1}$
2) $f(x) = \sqrt{256} \cdot \dfrac{1}{x}$		12) $f(x) = -2-\sqrt{\dfrac{1}{2}x}$
3) $f(x) = \vert-17\vert x$		13)
4) $f(x) = \dfrac{2}{x-8}$		14)
5) $f(x) = \left\vert\dfrac{1}{x^4}\right\vert$		15)
6) $f(x) = \sqrt{\vert x\vert}$		16)
7) $f(x) = -\left\vert\dfrac{2}{3}x\right\vert+6$		17)
8) $f(x) = \dfrac{\sqrt[3]{8}}{\sqrt{x}}$		18)
9) $f(x) = \left\vert \dfrac{1}{x+4}+5 \right\vert$		19)
10) $f(x) = \left\vert \sqrt{\vert x\vert}-2\right\vert$		20)

2. Aufgabe

1) Gegeben sei die Funktion $f(x)= \left\vert x-1 \right\vert +2$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=0$ b) wenn $y=6$		6) Gegeben sei die Funktion $f(x)=\left\vert -2x^2-20x+78 \right\vert$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=\dfrac{1}{3}$ b) wenn $y=0$
2) Gegeben sei die Funktion $f(x)= -\left\vert x-13 \right\vert +\dfrac{x}{2}$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=-24$ b) wenn $y=2$		7) Gegeben sei die Funktion $f(x)= - 4\left\vert (6x+5)(-26x-13)\right\vert-10$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=0$ b) wenn $y=-10$
3) Gegeben sei die Funktion $f(z)= 2 \cdot \left\vert z+4 \right\vert$ mit $z\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(z\mid y)$ , a) wenn $z=103$ b) wenn $y=20$		8) Gegeben sei die Funktion $f(x)= \left\vert x\right\vert \cdot x +4x-1$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=-21$ b) wenn $y=116$
4) Gegeben sei die Funktion $f(x)=\left\vert \dfrac{7}{2}x^2-2 \right\vert \cdot 3-\dfrac{9}{2}x^2$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=-\dfrac{4}{3}$ b) wenn $y=-18$		9) Gegeben sei die Funktion $s(t)= t \cdot \left\vert 3t\right\vert -23$ mit $t\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(t\mid y)$ , a) wenn $t=8$ b) wenn $y=256$
5) Gegeben sei die Funktion $f(x)= 12+ \left\vert x^3 \right\vert-150$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=-60$ b) wenn $y=-111$		10) Gegeben sei die Funktion $f(x)= -7\left\vert x^2-x \right\vert-6$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x = \dfrac{1}{8}$ b) wenn $y= -6$

3. Aufgabe

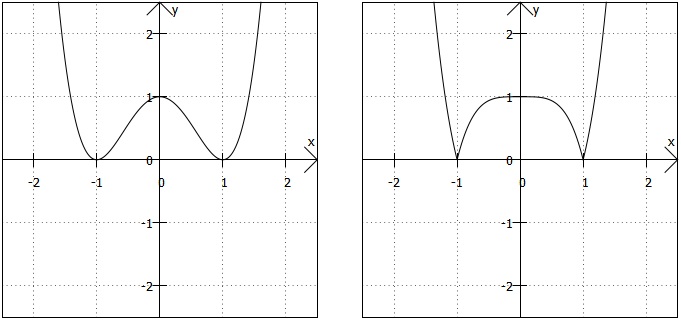
Was fällt Ihnen auf, wenn Sie die folgenden zwei Graphen vergleichen? Wie erklären Sie sich die Unterschiede?

zwei Funktionen zum Vergleich