SOS Mathematik
Dieses Kapitel enthält die folgenden Themen:
- Definition
- Polynomgleichungen
- Lösungsweg: Umformen
- Lösungsweg: Ausklammern
- Lösungsweg: Substitution
- Lösungsweg: Polynomdivision
- Polynomfunktionen
- Spezielle Polynome
13.2 Polynomgleichungen und -funktionen - Erklärungen
In den Kapiteln 9 und 10 hatten wir uns quadratische Gleichungen und quadratische Funktionen angeschaut. Im Folgenden werden wir diese mathematischen Objekte verallgemeinern. Der Gedanke, dass in Gleichungen und Funktionen auch Potenzen mit einem Exponenten größer als auftauchen können, liegt ja nicht allzu fern. Beispielsweise werden solche Gleichungen und Funktionen gebraucht, wenn Volumina betroffen sind. Man sieht ja schon an Einheiten wie
, dass man mit Quadraten offensichtlich nicht auskommt. In einem ingenieurwissenschaftlichen Studium werden Sie zudem später lernen, dass es sehr hilfreich sein kann, komplizierte Funktionen durch Polynome anzunähern (Stichwort: Taylorpolynom).
Sprachlich ist man hier häufig etwas ungenau und sagt einfach nur "Polynom" - egal, ob man eine Polynomgleichung oder eine Polynomfunktion meint. Was gemeint ist und was man tun soll, wird dann aus dem Zusammenhang bzw. der Aufgabenstellung klar.
Definition
Definition einer Polynomgleichung: Polynomgleichungen sind Gleichungen, bei denen Potenzterme mit beliebigen natürlichen Exponenten, ggf. multipliziert mit einem Koeffizienten, addiert werden.
Definition einer Polynomfunktion: Polynomfunktionen sind Funktionen, bei denen Potenzterme mit beliebigen natürlichen Exponenten, ggf. multipliziert mit einem Koeffizienten, addiert werden.
Allgemeine Darstellung einer Polynomgleichung: mit
,
und
Allgemeine Darstellung einer Polynomfunktion: mit
,
und
Die Gleichungen/Funktionen, die wir in vorherigen Kapiteln angeschaut haben, sehen ziemlich ähnlich aus, nur mit weniger Bestandteilen. Wenn Sie sich z. B. das "Ende" der allgemeinen Polynomgleichung ansehen, bleibt genau eine quadratische Gleichung übrig: .
Die reellen Zahlen heißen Koeffizienten des Polynoms. Da wir es hier mit reellen Zahlen zu tun haben, sind natürlich auch Brüche als Koeffizienten möglich. Wichtig: Da es sich bei den Koeffizienten um Zahlen handelt, ist klar, dass Variablen darin nicht vorkommen dürfen. Insbesondere dürfen Variablen nicht im Nenner eines Bruches stehen.
Die natürliche Zahl heißt Grad des Polynoms. Der Grad des Polynoms entspricht also dem höchsten Exponenten, der in dem Polynom vorkommt. Wichtig: Der Koeffizient dieses höchsten Potenzterms darf nicht
sein:
. Wäre
, würde diese Potenz ja wegfallen. Das hatten wir bei quadratischen Gleichungen ja auch schon diskutiert.
Definitionsbereich: Aus mathematischer Sicht gibt es keine Einschränkungen für den Definitionsbereich von Polynomen. Er umfasst also die gesamten reellen Zahlen, solange keine inhaltlichen Einschränkungen vorliegen (z. B. sollten die Maße eines Zylinders, für den das Volumen berechnet werden soll, positiv sein).
Polynomgleichungen
Starten wir mit ein paar Beispielen:
Dies ist ein Polynom vom Gradmit den Koeffizienten
,
,
und
.
Dies ist ein Polynom vom Gradmit den Koeffizienten
,
,
,
und
. Der Grad ist
, da der Koeffizient vom
-Term
ist.
Dies ist kein Polynom, weil die Variable beiim Nenner steht.
Lösungswege
Es gibt verschiedene Lösungsverfahren für Polynomgleichungen, die wir uns im Folgenden an verschiedenen Beispielen genauer anschauen werden. Bei manchen Polynomgleichungen benötigt man keine neuen mathematischen Verfahren. Zum Lösen genügen Methoden, die wir bereits in vorherigen Kapiteln kennengelernt haben. Wir müssen sie nur etwas kombinieren.
Leider gibt es bei allgemeinen Polynomgleichungen höheren Grades - anders als bei linearen und quadratischen Gleichungen - nur in Ausnahmefällen elementare Lösungsverfahren. Ein elementares Lösungsverfahren bei quadratischen Gleichungen ist z. B. die p-q-Formel, mit der man ohne große Komplikationen die Lösungen erhält. Das Lösen von Polynomgleichungen höheren Grades verläuft nur dann ähnlich unkompliziert, wenn die Gleichungen eine bestimmte Struktur aufweisen. Andernfalls kann das Lösen von Polynomen höheren Grades ziemlich aufwendig oder sogar unmöglich sein, sodass Lösungen nur näherungsweise bestimmt werden können. Solche Näherungsverfahren nennt man auch numerische Verfahren. Wenn nötig, werden Sie diese im Studium kennenlernen.
Umformen
Manche Polynomgleichungen kann man so umformen, dass auf einer Seite der Gleichung nur noch steht (mathematisch gesprochen: "man isoliert
"). Anschließend kommt man durch Wurzelziehen zur Lösung.
Struktur der Gleichung: Die Gleichung enthält nur einen Potenzterm, d. h. sie lässt sich in die Form bringen.
Bei Wurzeln mit geraden Wurzelexponenten aufpassen:
- Auch wenn solche Wurzeln im Bereich der reellen Zahlen immer nichtnegativ sind, entstehen beim Lösen der Gleichung zwei Lösungen, eine positive und eine negative.
- Steht unter einer solchen Wurzel eine negative Zahl, ist das Wurzelziehen nicht möglich.
Bei Wurzel mit ungeradem Wurzelexponenten kann beides nicht passieren. Nur beim Wurzelziehen aus negativen Radikanden muss man auf den Betrag aufpassen.
Ein Beispiel:
Und noch ein Beispiel:
Letztendlich funktioniert das genauso, wie wir das bei quadratischen Gleichungen - Lösungsweg: Umformen schon gesehen hatte, nur dass der Wurzelexponent ein anderer ist.
Ausklammern
Eine weitere Lösungsmöglichkeit ist das Ausklammern, das als erster Schritt immer eine gute Option ist, wenn die Struktur der Gleichung sich dafür eignet. Dadurch reduziert sich nämlich der Grad des Polynoms.
Struktur der Gleichung: Alle Summanden der Gleichung enthalten einen gemeinsamen Faktor, in dem auch die Variable bzw. Potenzen der Variablen enthalten sind.
Beispiel:
Zur 1. Zeile: Es rechnet sich einfacher, wenn vor dem nur eine
steht. Daher wird durch den Koeffizienten von
, also durch
, dividiert. Wichtig: Alle Terme der Gleichung müssen durch
dividiert werden! Andernfalls werden höchstwahrscheinlich genau die Probleme auftreten, die bereits im Kapitel lineare Gleichungen erläutert wurden.
Zur 2. Zeile: Als Nächstes sollen alle Terme auf der linken Seite der Gleichung gesammelt werden. Dazu wird gerechnet. Tipp: Für den Überblick ist es gut, die Terme so zu sortieren, dass der Term mit dem höchsten Exponenten immer zuerst steht und dann die übrigen Terme mit absteigendem Exponenten folgen.
Zur 3. Zeile: Es fällt auf, dass alle Summanden der Gleichung den Faktor enthalten. Das
kann also ausgeklammert werden.
Zur 4. Zeile: Nun haben wir die Gleichung in ein Produkt zweier Faktoren mit dem Ergebnis umgeformt, sodass uns der Satz vom Nullprodukt weiterhilft.
Ab der 5. Zeile: Nun betrachten wir die beiden Faktoren einzeln: Beim ersten Faktor (5. Zeile) ergibt sich die Lösung quasi von selbst. Beim zweiten Faktor (7. Zeile) müssen wir noch etwas weiterrechnen. Allerdings handelt es sich bei um eine einfache quadratische Gleichung, die mit der p-q-Formel gelöst werden kann.
Substitution
Bei der Lösung einer Gleichung durch Substitution werden komplizierte Gleichungen vereinfacht und damit in eine Form gebracht, in der wir sie lösen können. Der Begriff "Substitution" leitet sich vom lateinischen Wort "substituere" ab, welches "ersetzen" bedeutet - genau das tun wir bei einer mathematischen Substitution: Wir ersetzen (vorübergehend) kompliziertere Terme durch einfachere. Substituiert man bei Polynomen, ist es das Ziel, dass die Exponenten kleiner werden (z. B. und
), sodass man idealerweise am Ende die p-q- oder die a-b-c-Formel anwenden kann.
Im Anschluss an das folgende Beispiel 1 werden die einzelnen Schritte erläutert.
Struktur der Gleichung: In einer Gleichung sind nur Terme enthalten, die "Varianten" eines Ausgangsterms sind.
Beispiel 1:
Struktur der Gleichung: In der Gleichung sind alle Terme Varianten von
. Wir ersetzen dieses
durch
. Aus
wird dann
.
Falls Sie sich gefragt haben, was mit der ist: Auch diese ist - wenn man es mathematisch ganz genau nimmt - eine Variante von
, nämlich
, und passt damit ins Muster.
Substitution:
Rücksubstitution:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert die Rücksubstitution von keine weiteren Lösungen:
Erläuterung der einzelnen Schritte:
- Schritt - Substitution: Beim Substituieren wird der Ausgangsterm durch eine neue Variable ersetzt, meist
oder
. Dadurch wird die Gleichung deutlich handlicher.
- Schritt - Lösen der vereinfachten Gleichung: Je nach Gestalt der so entstandenen Gleichung kommen verschiedenste Verfahren zum Lösen der Gleichung infrage. In Beispiel oben entsteht eine "normale" quadratische Gleichung, die mithilfe der p-q-Formel gelöst werden kann.
- Schritt - Rücksubstitution: Zum Abschluss muss die Substitution rückgängig gemacht werden, da ja Lösungen für
und nicht für
oder
gesucht waren.
Natürlich muss der Ausgangsterm, der substituiert wird, nicht immer sein. Daher nun ein zweites Beispiel ... In späteren Kapiteln bei anderen Gleichungstypen werden Sie sehen, dass man noch ganz andere Terme substituieren kann. Daher ist es wichtig, sich hier schon mal mit diesem Vorgehen vertraut zu machen.
Beispiel 2:
Struktur der Gleichung: In der Gleichung sind alle Terme Varianten von
. Wir ersetzen dieses
durch
Aus
wird somit
und aus
wird
. Achtung:
wäre hier kein guter Name für die substituierte Variable, weil ja die Variable der Ausgangsgleichung schon so heißt.
Substitution:
Rücksubstitution:
Polynomdivision
Ein ziemlich wichtiges Verfahren beim Lösen von Polynomgleichungen ist die Polynomdivision. Dabei wird - wie der Name schon vermuten lässt - ein Polynom durch ein anderes dividiert. Vorteil dieses Verfahrens ist, dass der Grad des Ausgangspolynoms kleiner wird. Man sagt, "das Polynom wird reduziert". Wenn man Glück hat, ist irgendwann der Punkt erreicht, an dem für den restlichen Lösungsweg Verfahren wie die p-q-Formel weiterhelfen. Abhängig vom Grad der Polynome muss man dafür ggf. mehrfach dividieren. Nachteile dieses Verfahrens sind, dass man eine Lösung schon kennen muss, damit man anfangen kann, die übrigen zu berechnen, und nicht immer erhält man bei Anwendung der Polynomdivision am Ende alle Lösungen ...
Bevor wir uns intensiver mit der Polynomdivision beschäftigen, gehen wir nochmal einen Schritt zurück - so etwa in unsere Grundschulzeit - und erinnern uns an das schriftliche Dividieren von zwei natürlichen Zahlen. Im Großen und Ganzen funktioniert das Dividieren von zwei Polynomen nämlich genauso.
Ein Beispiel für die schriftliche Division: Berechnet werden soll . Dafür müssen wir drei Schritte so oft wiederholen, wie Stellen im Dividenden vorhanden sind.
- 1. Stelle:
- Wir prüfen zunächst, wie oft der Divisor, also die
, in die erste Stelle vom Dividenden, in diesem Fall in die
, passt. Das ist 1-mal der Fall. Die
notieren wir hinter dem Gleichheitszeichen.
- Wir multiplizieren "rückwärts", also die gerade gefundene
mit dem Divisor von oben:
und notieren das Ergebnis unter der ersten Stelle vom Dividenden, also unter der
.
- Wir subtrahieren die
von der
, schreiben das Ergebnis unter die Rechnung und ergänzen dort die nächste Stelle vom Dividenden, in diesem Fall die
.
- Wir prüfen zunächst, wie oft der Divisor, also die
- 2. Stelle:
- Wir prüfen, wie oft der Divisor in die unterste Zeile unserer Rechnung, in diesem Fall in die
, passt. Das ist 2-mal der Fall. Die
notieren wir hinter dem Gleichheitszeichen und der
.
- Wir multiplizieren "rückwärts":
und notieren das Ergebnis unter der Rechnung, also unter der
.
- Wir subtrahieren die
von der
, schreiben das Ergebnis unter die Rechnung und ergänzen dort die nächste Stelle, in diesem Fall die
.
- Wir prüfen, wie oft der Divisor in die unterste Zeile unserer Rechnung, in diesem Fall in die
- 3. Stelle:
- Wir prüfen wieder, wie oft der Divisor in die unterste Zeile unserer Rechnung, in diesem Fall in die
, passt. Das ist gar nicht der Fall. Wir notieren also eine
hinter dem Gleichheitszeichen und der
.
- Wir multiplizieren "rückwärts":
und notieren das Ergebnis unter der Rechnung, also unter der
.
- Wir subtrahieren die
von der
, schreiben das Ergebnis unter die Rechnung und ergänzen dort die nächste Stelle, in diesem Fall die
.
- Wir prüfen wieder, wie oft der Divisor in die unterste Zeile unserer Rechnung, in diesem Fall in die
- 4. Stelle:
- Wir prüfen noch einmal, wie oft der Divisor in die unterste Zeile unserer Rechnung, in diesem Fall in die
, passt. Das ist 6-mal der Fall. Die
notieren wir hinter dem Gleichheitszeichen und der
.
- Wir multiplizieren "rückwärts":
und notieren das Ergebnis unter der Rechnung, also unter der
.
- Wir subtrahieren die
von der
und schreiben das Ergebnis unter die Rechnung.
- Wir prüfen noch einmal, wie oft der Divisor in die unterste Zeile unserer Rechnung, in diesem Fall in die
Probe: Um unsere Rechnung zu überprüfen, können wir das Ergebnis mit dem Divisor multiplizieren: . Passt!
Geschafft! Hoffentlich erinnern Sie sich daran ... Dann ist es nämlich bedeutend einfacher, die Polynomdivision zu durchschauen.
Kommen wir nun konkret dazu, wie die Polynomdivision funktioniert. Die drei sich wiederholenden Schritte sind dabei die gleichen wie oben, nur dass noch ein paar Variablen im Spiel sind. Auch hier nehmen wir uns ein Beispiel vor, nämlich die Polynomgleichung , bei der die weiter oben besprochenen Lösungsverfahren nicht weiterhelfen. Um die Polynomdivision durchführen zu können, benötigen wir die Information, dass
eine der Lösungen ist. Das sinnvollste Vorgehen, wie man das herausfindet, schauen wir uns weiter unten an.
Durch die Polynomdivision wird das ursprüngliche Polynom in ein Produkt zweier Faktoren zerlegt. Wichtig dabei ist, dass auf der anderen Seite der Gleichung steht. Denn nur so können wir uns im Anschluss den Satz vom Nullprodukt zunutze machen. Für die gegebene Lösung
muss mindestens einer der beiden Faktoren
werden, damit das gesamte Produkt
wird. Der Faktor
) erfüllt genau diese Anforderung. (Wäre die gegebene Lösung
, bekämen wir den Faktor
). Letztendlich taucht die Lösung im Faktor immer mit umgekehrtem Vorzeichen auf. Ziel der Polynomdivision ist es, noch den zweiten Faktor zu bestimmen. Hierfür dividieren wir das Polynom durch unseren Faktor. Damit kann es losgehen:
- 1. Schritt:
- Wir prüfen, wie oft das
vom Divisor in den ersten Term des Dividenden, in diesem Fall in
, passt. Das ist
-mal der Fall.
notieren wir hinter dem Gleichheitszeichen.
- Wir multiplizieren "rückwärts":
und notieren das Ergebnis unter dem Dividenden, also unter
.
- Wir subtrahieren
von
. Daher steht in unserer Rechnung in der zweiten Zeile
. Das Ergebnis schreiben wir unter die Rechnung und ergänzen dort den nächsten Term des Dividenden, in diesem Fall
. Beim Subtrahieren darauf achten, dass natürlich nur Potenzen mit gleichem Exponenten zusammengerechnet werden dürfen (Potenz- vor Punkt- vor Strichrechnung!).
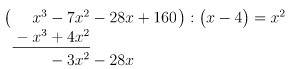
- Wir prüfen, wie oft das
Zur Notation: Ganz wichtig: In der ersten Zeile der Rechnung müssen um Dividend und Divisor auf alle Fälle Klammern gesetzt werden! Sonst würden in diesem Beispiel nur und
durcheinander geteilt werden - Punktrechnung geht ja vor Strichrechnung!
Bemerkung: Den Satz beim 1. Unterpunkt "Wir prüfen, wie oft das vom Divisor in den ersten Term des Dividenden, in diesem Fall in
, passt." könnte man auch so formulieren: "Wir prüfen, mit welchem Faktor man das
vom Divisor multiplizieren muss, um den ersten Term des Dividenden, in diesem Fall in
, zu erhalten."
- 2. Schritt:
- Wir prüfen nun, wie oft das
vom Divisor in den ersten Term der untersten Zeile, in diesem Fall in
, passt. Das ist
-mal der Fall.
notieren wir hinter dem Gleichheitszeichen und dem
.
- Wir multiplizieren "rückwärts":
und notieren das Ergebnis unter dem Dividenden, also unter
.
- Wir subtrahieren
von
, schreiben das Ergebnis unter die Rechnung und ergänzen dort den nächsten Term des Dividenden, in diesem Fall
.
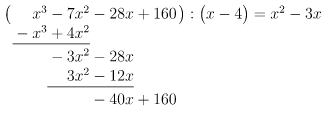
- Wir prüfen nun, wie oft das
- 3. Schritt:
- Wir prüfen noch einmal, wie oft das
vom Divisor in den ersten Term der untersten Zeile, in diesem Fall in
, passt. Das ist
-mal der Fall.
notieren wir hinter dem Gleichheitszeichen und dem
.
- Wir multiplizieren "rückwärts":
und notieren das Ergebnis unter dem Dividenden, also unter
.
- Wir subtrahieren
von
und schreiben das Ergebnis unter die Rechnung.
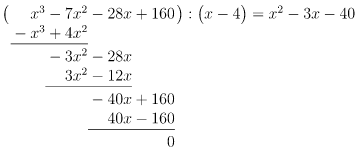
- Wir prüfen noch einmal, wie oft das
Auch hier: Geschafft!
Das reduzierte Polynom ist quadratisch, sodass wir mithilfe der p-q-Formel die restlichen Lösungen ermitteln können:
.
Bemerkung 1: Diese Polynomdivision ist ohne Rest aufgegangen, was die Bestätigung dafür ist, dass tatsächlich eine Lösung der Gleichung ist. Natürlich kann bei der Polynomdivision auch ein Rest bleiben. Dann war die angenommene Lösung doch keine (Dafür gibt es gleich das 1. Beispiel.) oder man hat sich verrechnet ...
Bemerkung 2: Hinter dem Gleichheitszeichen der letzten Rechnung steht das sogenannte "reduzierte Polynom", welches in diesem Fall quadratisch ist. Das muss aber nicht immer der Fall sein. Das reduzierte Polynom kann natürlich auch einen anderen Grad haben. Dazu schauen wir uns weiter unten noch das 2. Beispiel an.
Merke: Der Grad des reduzierten Polynoms entspricht immer dem Grad vom Ausgangspolynom minus dem Grad vom Divisor.
Wie bei der schriftlichen Division können wir zur Überprüfung unserer Rechnung eine Probe durchführen, indem wir das Ergebnis mit dem Divisor multiplizieren:
Stimmt also!
Zwei etwas andere Beispiele für die Polynomdivision:
1. Beispiel:
Wie bei der Division natürlicher Zahlen ist es natürlich auch möglich, dass bei einer Polynomdivision ein Rest bleibt: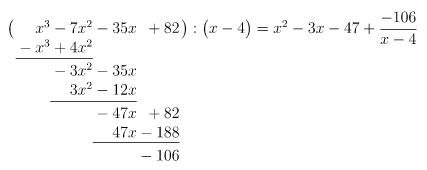
In diesem Fall ist keine Lösung der Ausgangsgleichung. Hinter dem Gleichheitszeichen steht auch nicht das reduzierte Polynom - da im letzten Summand durch die Variable geteilt wird, handelt es sich bei
nicht um ein Polynom, sondern um etwas gebrochen Rationales ...
Die Rechnung wird abgebrochen, wenn der Grad des Polynoms in der untersten Zeile kleiner ist als der Grad des Divisors. Diese Variante kommt vor allem bei gebrochen rationalen Funktionen vor, um diese integrieren zu können oder den globalen Verlauf zu erkennen.
2. Beispiel:
Polynomdivision ist auch mit einem quadratischen Divisor möglich: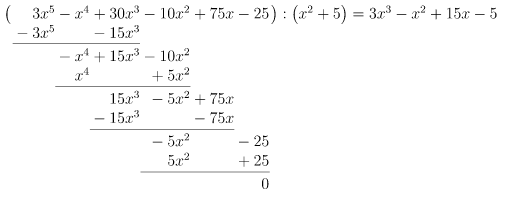
Der Ablauf der Polynomdivision bleibt so wie oben besprochen. Wir prüfen natürlich in diesem Fall, wie oft das vom Divisor in den ersten Term des Dividenden passt. Es muss dann darauf geachtet werden, dass sich der Grad der Terme beim Rückmultiplizieren jeweils um
unterscheidet. Daher bleiben beim Subtrahieren "Lücken", da ja nur Potenzen mit gleichem Exponenten zusammengerechnet werden dürfen (Potenz- vor Punkt- vor Strichrechnung!). Man muss hier also (noch) ein bisschen besser aufpassen ...
Zum Abschluss noch ein paar Worte, wie man die erste Lösung finden kann:
- Zunächst kann in vielen Fällen die grafische Darstellung des Polynoms helfen.
- Ansonsten bleibt einem hier (anders als sonst in der Mathematik) nicht viel mehr übrig als Raten und Probieren. Die besten Kandidaten zum Probieren sind die Teiler des konstanten Terms. Es gilt nämlich: Hat eine Polynomfunktion nur ganzzahlige Koeffizienten und besitzt ganzzahlige Nullstellen, dann ist eine der Nullstellen ein Teiler des konstanten Terms.
Bei unserer Gleichungist dies die
mit den Teilern
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
und
.
Für:
Für:
Für:
Für:
Für:
Allerdings ist es nicht gesagt, dass man tatsächlich immer eine Lösung durch Probieren finden kann. Nehmen wir als Beispiel das Polynom . Die Teiler des konstanten Terms
sind
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
und
. Wenn wir uns den Graphen der zugehörigen Polynomfunktion anschauen, sehen wir, dass keiner dieser Teiler eine Lösung sein kann:
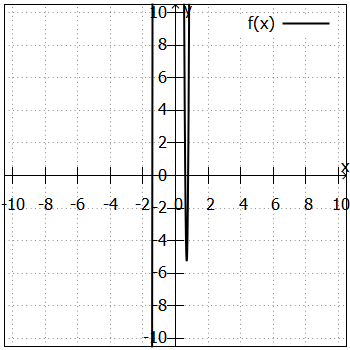
Die Lösungen sind ,
und
. Das kann man durch einfaches Probieren nicht herausfinden. Insofern helfen uns die beiden oben genannten Strategien hier nicht weiter. Wir finden keine Lösung, mit der wir eine Polynomdivision durchführen könnten. In solchen Fällen bleibt die Situation also leider unklar: Findet man einfach nur keine weiteren Lösungen (Man kann ja mal etwas übersehen ...) oder gibt es tatsächlich keine? Auf diese Frage gibt es keine Antwort. Ganzzahlige Lösungen lassen sich verhältnismäßig leicht finden - aber gebrochene Lösungen (wie hier) oder irrationale (wie
) sollen ja auch mal vorkommen ... Dann kommt man mit der Polynomdivision leider nicht weiter.
So, nun kennen Sie die wichtigsten Verfahren zum Lösen von Polynomgleichungen. Es gibt allerdings keine Garantie, dass man damit tatsächlich zur Lösung einer gegebenen Gleichung kommt. Was man in jedem Fall weiß: Die Anzahl der Lösungen einer Polynomgleichung ist im Bereich der reellen Zahlen maximal so groß wie der Grad des Polynoms. Anders formuliert: Polynome vom Grad haben im Bereich der reellen Zahlen maximal
Lösungen. In etwas verallgemeinerter Form steckt diese Erkenntnis im sogenannten "Fundamentalsatz der Algebra" und geht auf die Doktorarbeit von Carl Friedrich Gauß zurück. Das liefert einem zumindest eine "Obergrenze", ab der man weiß, dass es keine weiteren Lösungen mehr geben kann.
Polynomfunktionen
Kommen wir nun zu den Polynomfunktionen. Statt Polynomfunktion sagt man manchmal auch ganz rationale Funktion. Das ist einfach nur ein anderer Begriff und meint genau das Gleiche. Wir werden uns in den folgenden Abschnitten anschauen, welche Eigenschaften und "besondere Punkte" sie haben. Entscheidend ist dabei meistens, ob der Grad der Polynomfunktion gerade oder ungerade ist, wobei wir im Folgenden nur Polynome mit einem Grad von mindestens betrachten.
Um genau zu sein, ist auch die Funktion eine Polynomfunktion geraden Grades. Allerdings ist dieser Sonderfall eines geraden Polynoms so einfach (man könnte auch sagen, er ist trivial), dass es sich nicht lohnt, hier viele Worte zu verlieren ... Alles Wissenswerte dazu können Sie im Kapitel über lineare Funktionen nachlesen.
Randverhalten
Bei Polynomen geraden Grades gibt es zwei Möglichkeiten für das Randverhalten: Entweder liefern sowohl sehr kleine x-Werte als auch sehr große x-Werte sehr große Funktionswerte (Anders formuliert: Der Funktionswert geht gegen .) oder sowohl sehr kleine x-Werte als auch sehr große x-Werte liefern sehr kleine Funktionswerte. "Sehr klein" bedeutet dabei, dass es sich um negative Zahlen mit einem sehr großen Betrag handelt, z. B.
. Der Funktionswert geht also gegen
.
Hintergrund ist, dass die höchste Potenz in einem Polynom den entscheidenden Einfluss auf den Gesamtverlauf des Graphen hat. Beispielsweise ist für sehr kleine und sehr große x-Werte deutlich größer als
und überlagert damit den Effekt, den
auf den Verlauf des Graphen nimmt. Außerdem sind Potenzen mit geradem Exponenten immer nichtnegativ, weil "minus mal minus gleich plus" ist. Das Vorzeichen vom Koeffizienten der höchsten Potenz "entscheidet" also, ob die Funktionswerte für sehr kleine und sehr große x-Werte positiv oder negativ sind.
Auch für Polynome ungeraden Grades gibt es zwei mögliche Verläufe: Entweder gehen die Funktionswerte für sehr kleine x-Werte gegen und die für sehr große x-Werte gegen
. Oder umgekehrt. Wieder liegt es am Vorzeichen vom Koeffizienten der höchsten Potenz, welcher Verlauf vorliegt.
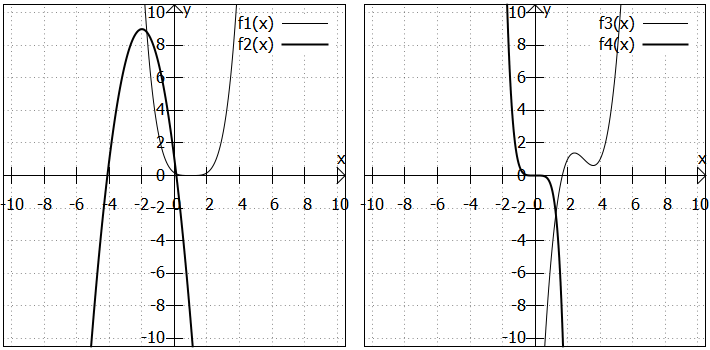
In der linken Grafik sind zwei Polynome geraden Grades abgebildet, in der rechten Grafik zwei Polynome ungeraden Grades. Schauen wir uns das Randverhalten dieser Polynome genauer an:
- Das Polynom
hat einen geraden Grad und die höchste Potenz einen positiven Koeffizienten. Da
nichtnegativ ist für alle x-Werte und der Koeffizient
am Vorzeichen nichts ändert, verläuft
von
nach
.
- Bei
hat die höchste Potenz einen geraden Exponenten und ihr Koeffizient ist negativ. Der Graph ist nach unten geöffnet. Entsprechend gehen die Funktionswerte für sehr kleine und sehr große x-Werte gegen
.
- Das Polynom
hat einen ungeraden Grad und die höchste Potenz einen positiven Koeffizienten.
ist negativ für negative x-Werte und positiv für positive x-Werte. Der Koeffizient
ändert daran nichts, also verläuft
von
nach
.
- Umgekehrt ist es bei
. Der Potenzterm
ist zwar auch negativ für negative x-Werte und positiv für positive x-Werte. Durch die Multiplikation mit
verläuft der Graph von
nach
.
Symmetrie
Polynome mit ausschließlich geraden Exponenten (auch "gerade Polynome" genannt) sind achsensymmetrisch zur y-Achse, da solche Polynome die Bedingung immer erfüllen.
Polynome mit ausschließlich ungeraden Exponenten (auch "ungerade Polynome" genannt) sind punktsymmetrisch zum Koordinatenursprung, da solche Polynome die Bedingung immer erfüllen.
Bitte beachten Sie, dass ein konstanter Term im Polynom einen geraden Exponenten hat, da man dort ja ein ergänzen könnte, und
eine gerade Zahl ist.
Polynome mit beliebigen Exponenten sind weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Koordinatenursprung, können aber zu anderen Geraden bzw. Punkten symmetrisch sein.
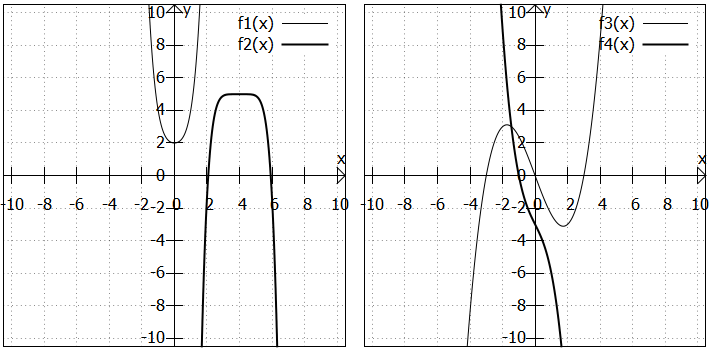
In der linken Grafik sind zwei Polynome geraden Grades abgebildet, in der rechten Grafik zwei Polynome ungeraden Grades. Sie sehen:
ist als gerades Polynom achsensymmetrisch zur y-Achse.
- Löst man bei
die Klammer auf, erhält man
, also ein Polynom mit geraden und ungeraden Exponenten. Der Graph von
kann also nicht achsensymmetrisch zur y-Achse sein. Er ist aber achsensymmetrisch zur senkrechten Gerade durch
. Das überrascht nicht sehr, wenn wir uns die zusammengefasste Form anschauen: Die
in der Klammer bewirkt ja gerade eine Verschiebung des Graphen um
Einheiten nach rechts. Die
hinter der Klammer bewirkt eine Verschiebung des Graphen um
Einheiten nach oben (was aber auf die Achsensymmetrie keinen Einfluss hat).
ist als ungerades Polynom punktsymmetrisch zum Koordinatenursprung.
- Achten Sie bei
darauf, dass dies kein Polynom mit ausschließlich ungeraden Exponenten ist (auch wenn es auf den ersten Blick vielleicht so aussieht). Entsprechend ist sein Graph nicht punktsymmetrisch zum Ursprung. Er ist punktsymmetrisch zum Punkt
.
Nullstellen
Die Anzahl der Nullstellen eines Polynoms ist im Bereich der reellen Zahlen maximal so groß wie sein Grad. Anders formuliert: Polynome vom Grad haben im Bereich der reellen Zahlen maximal
Nullstellen.
Polynome, die keinen konstanten Term enthalten, haben immer mindestens eine Nullstelle, nämlich . Umgekehrt formuliert: Wenn alle Summanden im Polynom die Variable enthalten, ist der Funktionswert für
immer
, z. B. bei
.
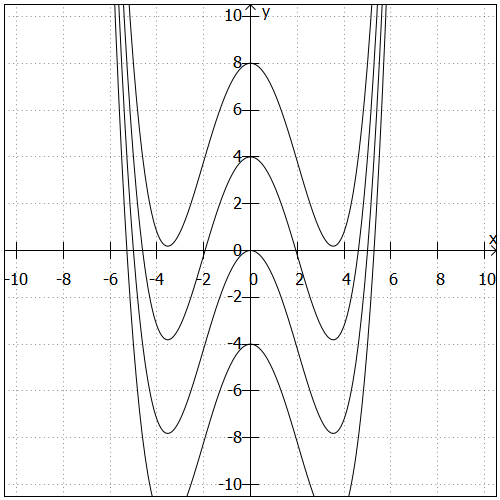
In der folgenden Grafik sind verschiedene Varianten des Polynoms geraden Grades dargestellt. Wir wissen, dass maximal vier Nullstellen auftreten können, da es sich um ein Polynom vierten Grades handelt. Die konkrete Zahl der Nullstellen ist aber abhängig von der Konstanten, die zum Funktionsterm addiert wird:
- Die oberste der abgebildeten Funktionen
hat keine Nullstellen.
- Die zweitoberste der abgebildeten Funktionen
hat vier Nullstellen.
- Die zweiunterste der abgebildeten Funktionen
hat drei Nullstellen.
- Die unterste der abgebildeten Funktionen
hat zwei Nullstellen.
Polynome ungeraden Grades haben mindestens eine Nullstelle. Wenn Sie sich an das Randverhalten von Polynomen ungeraden Grades erinnern, kann das auch gar nicht anders sein: Ein Graph, der ohne Sprünge und Lücken von nach
verläuft (oder umgekehrt), muss ja die x-Achse mindestens einmal schneiden.
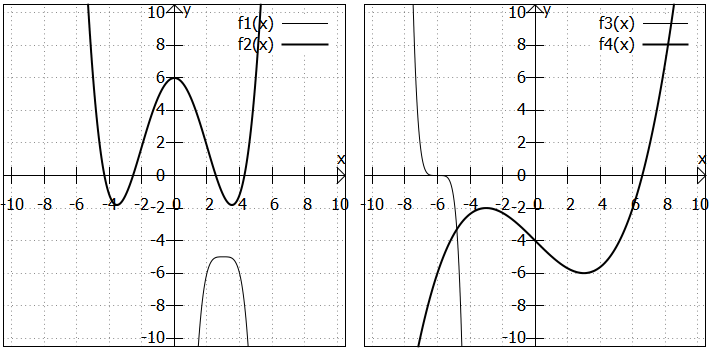
In der folgenden Grafik sind verschiedene Varianten der Funktion dargestellt. Da es sich um ein Polynom dritten Grades handelt, können maximal drei Nullstellen auftreten. Abhängig von der Konstanten, die addiert wird, ändert sich auch hier die Zahl der Nullstellen. Allerdings bewirkt keine Konstante, dass die Funktion vollständig über oder vollständig unter der x-Achse liegt:
- Die oberste der abgebildeten Funktionen
hat eine Nullstelle.
- Die mittlere der abgebildeten Funktionen
hat zwei Nullstellen.
- Die unterste der abgebildeten Funktionen
hat drei Nullstellen.

Extrempunkte
Polynome vom Grad haben im Bereich der reellen Zahlen maximal
Extrempunkte. Ob es sich dabei um Hoch- oder um Tiefpunkte handelt, hängt vom konkreten Verlauf des Graphen ab.
Bei so vernünftig verlaufenden Funktionen wie Polynomen, die keine Sprünge, Lücken oder sonstige Auffälligkeiten haben, liegt zwischen zwei Hochpunkten immer ein Tiefpunkt und zwischen zwei Tiefpunkten immer ein Hochpunkt. Salopp formuliert: Wenn Sie auf einem Gipfel stehen, müssen Sie erstmal ins Tal, bevor Sie den nächsten Gipfel erklimmen können.
Auch zwischen zwei Nullstellen muss immer mindestens ein Extrempunkt liegen (Ausnahme ist das Polynom , was ja quasi nur aus Nullstellen besteht.). Umgekehrt gilt dies aber nicht: Ein Extrempunkt muss nicht immer zwischen zwei Nullstellen liegen. Eine Funktion, die beispielsweise so weit nach oben verschoben ist, dass sie die x-Achse nicht schneidet, darf ja trotzdem Extrempunkte haben.
Polynome geraden Grades haben immer mindestens ein Extrempunkt. Bei Polynomen ungeraden Grades weiß man nicht, ob sie Extrempunkte haben oder nicht. Beides ist möglich.
Wende- und Sattelpunkte
Polynome vom Grad haben im Bereich der reellen Zahlen maximal
Wende- bzw. Sattelpunkte.
Bei Polynomfunktionen, die ja - wie oben schon erwähnt - vernünftig verlaufen, muss sich zwischen zwei Extrempunkten immer mindestens ein Wendepunkt befinden. Allerdings müssen zwischen zwei Wendepunkten nicht zwingend auch Extrempunkte liegen.
Bei Polynomen geraden Grades kann man allgemein nichts über das Vorhandensein von Wende- und Sattelpunkten sagen: Sie können welche haben oder auch nicht. Polynome ungeraden Grades haben immer mindestens einen Wende- bzw. Sattelpunkt.
In der linken Grafik sind wieder zwei Polynome geraden Grades abgebildet, in der rechten Grafik zwei Polynome ungeraden Grades. Sie sehen:
- Da das Polynom geraden Grades
ein verschobenes, nach unten geöffnetes
-Polynom mit dem Hochpunkt
ist, hat der Graph keinen Wende- oder Sattelpunkt, sondern nur einen Hochpunkt.
- Bei
, ebenfalls ein Polynom geraden Grades, passiert mehr: Es hat zwei Wendepunkt bei
und
, dazu vier Nullstellen und drei Extrempunkte.
- Das Polynom ungeraden Grades
hat einen Sattelpunkt bei
, der gleichzeitig Nullstelle ist. Hoch- und Tiefpunkte gibt es nicht.
- Bei dem Polynom
ist der Wendepunkt
eingerahmt von zwei Extrempunkten. Eine Nullstelle gibt es auch noch.
Polstellen
Da Polynome aus mathematischer Sicht für die gesamten reellen Zahlen definiert sind und somit keine Definitionslücken haben, können keine Polstellen auftreten. Auch Einschränkungen des Definitionsbereichs aufgrund inhaltlicher Rahmenbedingungen erzeugen keine Polstellen.
Spezielle Polynome
Einige häufig auftretende Polynome haben spezielle Bezeichnungen - unabhängig davon, ob es sich um eine Polynomgleichung oder eine Polynomfunktion handelt ():
- Konstantes Polynom:
- Lineares Polynom:
bzw.
mit
Statt "lineares Polynom" kann man auch "Polynom ersten Grades" sagen. Egal, wie man solche Polynome nennt, Sie kennen sie schon aus den Kapiteln lineare Gleichungen und lineare Funktionen. - Quadratisches Polynom:
bzw.
mit
Statt "quadratisches Polynom" kann man auch "Polynom zweiten Grades" sagen. Auch diese Polynome kennen Sie schon aus den Kapiteln quadratische Gleichungen und quadratische Funktionen. - Kubisches Polynom:
bzw.
mit
Statt "kubisches Polynom" sagt man häufig auch "Polynom dritten Grades". - Biquadratisches Polynom:
bzw.
mit
,
,
und
Ein biquadratisches Polynom ist ein spezielles Polynom vierten Grades, bei dem die Koeffizientenund
immer
sind. Es bleiben also nur die Potenzen
und
(ggf. mit Koeffizienten) und eventuell der konstante Term übrig.