SOS Mathematik
Dieses Kapitel enthält die folgenden Themen:
- Allgemeines zur quadratischen Funktion
- Strecken und Stauen einer Parabel
- Verschieben einer Parabel
- Quadratische Ergänzung
- Weitere interessante Punkte einer Parabel
10.2 Quadratische Funktionen - Erklärungen
So, wie es zu den linearen Gleichungen lineare Funktionen gibt, gibt es auch quadratische Funktionen passend zu den quadratischen Gleichungen. Um diese wird es im Folgenden gehen. Es wird damit ein bisschen komplexer als bei linearen Funktionen - dafür auch etwas spannender.
Was man allgemein wissen sollte
Die allgemeine Gleichung einer quadratischen Funktion lautet: mit
(siehe Zahlenbereiche) oder auch
mit
. In beiden Fälle muss
sein, weil sonst der quadratische Term der Funktionsgleichung (oder sogar noch mehr) wegfällt. Das "Problem" kennen wir schon von den quadratischen Gleichungen.
Der Graph einer quadratischen Funktion ist eine Parabel. Schauen wir uns als Erstes den Graphen von , der einfachsten quadratischen Funktion, an. Dazu erstellen wir eine Wertetabelle mit einigen Funktionswerten:
Im Koordinatensystem sieht die Parabel dann so aus:
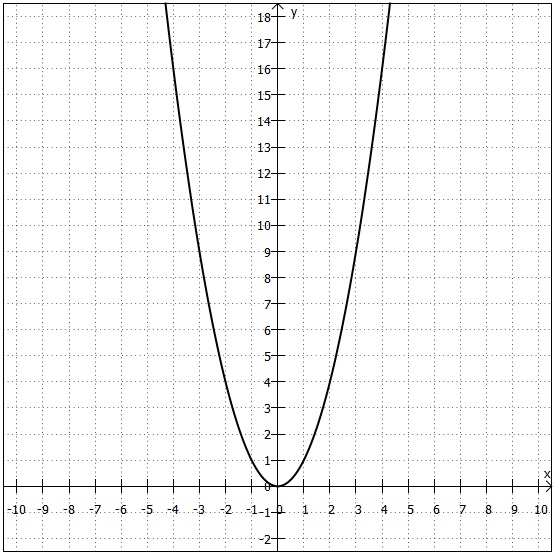
Es fällt auf, dass die Parabel für negative x-Werte fällt und für positive x-Werte steigt. Daher hat sie bei einen tiefsten Punkt. Dieser Verlauf ist typisch für Parabeln. Die Alternative zu diesem Verlauf ist, dass die Parabel für negative x-Werte steigt und für positive x-Werte fällt und damit einen höchsten Punkt hat (Beispiele dafür kommen etwas später im Laufe dieses Kapitels ...). Der tiefste bzw. höchste Punkt einer Parabel wird Scheitelpunkt genannt. Damit haben wir auch schon - bis auf Verschiebungen, um die wir uns weiter unten kümmern werden - alle möglichen Verläufe von Parabeln besprochen. Der Gegensatz zu linearen Funktionen, die entweder nur steigen oder nur fallen (wenn sie nicht konstant sind) und daher auch keinen höchsten oder tiefsten Punkt haben können, ist vermutlich offensichtlich.
In den nächsten Abschnitten schauen wir uns jeweils anhand von Beispielen an, was man mit einer Parabel im Koordinatensystem alles machen kann. In der allgemeinen Gleichung einer quadratischen Funktion tauchen mehrere Konstanten auf, die jeweils einen bestimmten Einfluss auf den Verlauf der Parabel haben. Diese Einflüsse gibt es nicht bloß bei Parabeln sondern bei jedem Funktionsgraphen, sodass wir hier einen Grundstein für die Betrachtung von ganz verschiedenen Funktionstypen legen.
Strecken und Stauchen einer Parabel
Schauen wir als erstes, wie die reelle Zahl aus der Parabelgleichung (
oder
) den Verlauf des Graphen beeinflusst: Da
die Kurzform für
ist (Sie wissen ja, eine
wird gerne mal weggelassen ...), hatten wir oben schon ein Beispiel dafür gesehen, dass Parabeln mit positivem
, also
, nach oben geöffnet sind.
Ist dabei größer als
, also
, dann wird die Parabel steiler. Mathematisch sagt man: Sie wird gestreckt. Beispielhaft schauen wir uns die Wertetabelle von
an. Sie sehen, dass die Funktionswerte alle deutlicher größer sind als bei
:
Der Graph von ist im folgenden Koordinatensystem als dünne Linie eingezeichnet.
Ist zwar positiv, aber kleiner als
, also
, dann wird die Parabel bauchiger. Mathematisch sagt man: Sie wird gestaucht. Das Beispiel hier ist
:
Der Graph von ist im folgenden Koordinatensystem als Linie mit Sternchen eingezeichnet. Als Vergleich ist der Graph von
als dicke Linie miteingezeichnet.
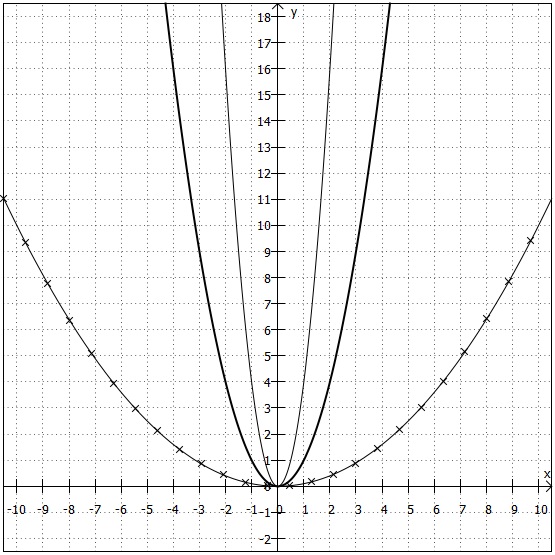
Sie sehen, dass die drei Parabeln sehr ähnlich verlaufen: Alle sind nach oben geöffnet. Alle haben den Scheitelpunkt im Punkt . Alle haben die typische Parabelform. Nur in der Streckung/Stauchung unterscheiden sich die drei Parabeln. In Abhängigkeit von
ändert sich also das Steigungsverhalten der Parabel.
Nun kann auch negativ sein, also
. Dann ist die Parabel nach unten geöffnet. Wir betrachten als Beispiel die einfachste quadratische Funktion mit einem negativen
, nämlich
:
Der Graph von ist im folgenden Koordinatensystem als dicke Linie eingezeichnet.
Ist dabei kleiner als
, also
, dann wird die Parabel wieder gestreckt, allerdings "kopfüber". Beispielhaft schauen wir uns die Wertetabelle von
an:
Der Graph von ist im folgenden Koordinatensystem als dünne Linie eingezeichnet.
Ist zwar negativ, aber größer als
, also
, dann wird die Parabel "kopfüber" gestaucht. Sie sehen das an der folgenden Wertetabelle für
:
Der Graph von ist im folgenden Koordinatensystem als Linie mit Sternchen eingezeichnet. Als Vergleich ist der Graph von
als dicke Linie miteingezeichnet.
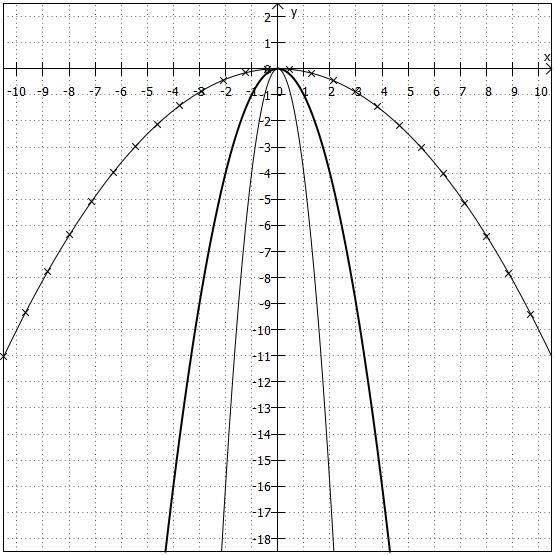
Die Erkenntnisse hier sind ziemlich analog zu oben ... Die drei Parabeln verlaufen sehr ähnlich: Diesmal sind alle nach unten geöffnet. Es bleibt dabei, dass alle den Scheitelpunkt im Punkt und die typische Parabelform haben. Nur in der Streckung/Stauchung gibt es wieder Unterschiede im Verlauf der drei Parabeln.
Wenn Sie diese Grafik mit der darüber vergleichen, sehen Sie, dass und
spiegelbildlich zueinander verlaufen. Gleiches gilt für
und
sowie für
und
. Was soll auch anderes passieren, wenn die Funktionswerte bis auf das Minuszeichen alle gleich sind?
Eine wichtige Vokabel noch in diesem Zusammenhang: Ist oder
, also bei
und
, wird die Parabel auch Normalparabel genannt.
Nun wäre es ein bisschen langweilig, wenn wir zwar verschieden gestreckte/gestauchte Parabeln erzeugen könnten, der Scheitelpunkt der Parabel aber immer im Koordinatenursprung liegen müsste ... Die übrigen Konstanten aus der Parabelgleichung machen es möglich, die Parabel im Koordinatensystem in alle Richtungen zu verschieben.
Verschieben einer Parabel
Auch hier schauen wir uns verschiedene Beispiele als Wertetabelle und als Graph an. Ausgangspunkt ist jeweils die sogenannte Scheitelpunktform einer quadratischen Gleichung mit
und
. Um
hatten wir uns im vorherigen Abschnitt schon gekümmert. Nun interessieren uns
und
.
In den folgenden beiden Grafiken ist der Graph von als dicke Linie zum Vergleich miteingezeichnet.
Wir nehmen eine positive reelle Zahl , also
.
Wahrscheinlich können Sie sich vorstellen, was bei passiert, wenn also zu den Funktionswerten von
jeweils
addiert wird ... Richtig: Alle Funktionswerte werden um
größer; der Graph wird also um
Einheiten nach oben verschoben. Besonders gut sieht man das am Scheitelpunkt. Als Beispiel haben wir hier
:
Der Graph von ist im folgenden Koordinatensystem als dünne Linie eingezeichnet.
Umgekehrt ist der Graph der Funktion gegenüber dem Graphen von
um
Einheiten nach unten verschoben. Wir schauen uns hier
an:
Der Graph von ist im folgenden Koordinatensystem als Linie mit Sternchen eingezeichnet.
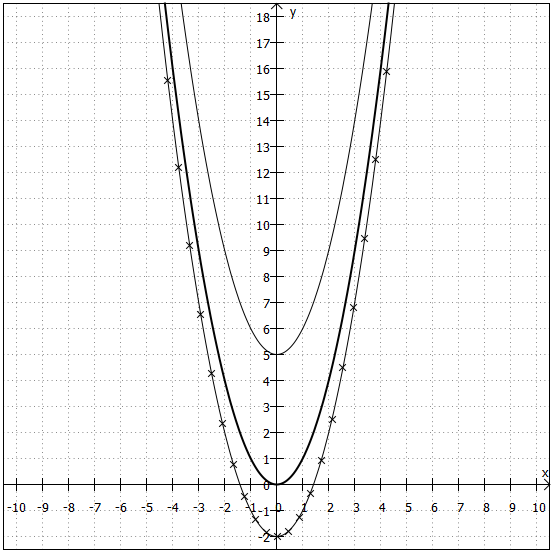
In beiden Fällen bleibt der Scheitelpunkt bei , aber sein Funktionswert ändert sich: Der Scheitelpunkt von
liegt im Punkt
. Bei
liegt der Scheitelpunkt im Punkt
. Da bei beiden Funktionen
ist, sind sie nicht gestreckt/gestaucht, sondern haben exakt die gleiche Form wie die mit einer dicken Linie eingezeichnete Normalparabel.
Zu guter Letzt: sei eine positive reelle Zahl, also
. Natürlich geht es jetzt um die Verschiebung nach rechts und links - allerdings funktioniert diese nicht ganz so, wie man es vielleicht erwartet:
Die Funktion ist gegenüber der Normalparabel um
Einheiten nach rechts verschoben. Ein negatives Vorzeichen in der Klammer führt also zu einer Verschiebung in positive x-Richtung. Schauen wir uns beispielhaft
an:
Der Graph von ist im folgenden Koordinatensystem als dünne Linie eingezeichnet.
Die Funktion ist gegenüber der Normalparabel um
Einheiten nach links verschoben. Ein positives Vorzeichen in der Klammer führt also zu einer Verschiebung in negative x-Richtung. Auch hier ein Beispiel:
Der Graph von ist im folgenden Koordinatensystem als Linie mit Sternchen eingezeichnet.
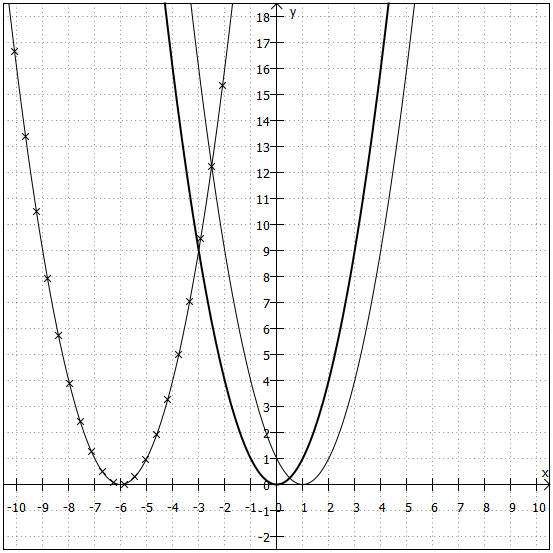
Sie sehen, dass der Scheitelpunkt in die "verkehrte" Richtung rutscht: Steht in der Klammer , ist die x-Koordinate des Scheitelpunkts
; bei
in der Klammer ist die x-Koordinate des Scheitelpunkts
.
Woran das liegt, schauen wir uns am Beispiel von an. Genauer, wir betrachten den Scheitelpunkt von
: Es handelt sich um eine nach oben geöffnete Parabel, da der Koeffizient von
positiv ist. Damit ist der Scheitelpunkt der niedrigste Punkt der Parabel, also der Punkt mit der kleinsten y-Koordinate (Das sehen Sie auch in der Grafik ...). Da Quadrate nie negativ werden können, ist
der kleinste Wert, den der Funktionsterm
annehmen kann. Wir müssen also die Frage beantworten, bei welchem x-Wert der Funktionsterm
wird, um zu sehen, wohin der Scheitelpunkt rutscht: Das passiert, wenn
ist, denn
. Der Scheitelpunkt von
liegt also im Punkt
. Der negative Wert
in der Parabelgleichung führt also dazu, dass der Scheitelpunkt in den positiven x-Bereich rutscht.
Umgekehrt führt ein positiver Wert in der Parabelgleichung dazu, dass der Scheitelpunkt im negativen x-Bereich liegt, weil
(also der Funktionsterm von
) dann
wird, wenn
ist.
Fazit: Lassen Sie sich von der auf den ersten Blick unlogischen Verschiebungsrichtung nicht irritieren! Am besten gelingt dies, wenn Sie sich am Scheitelpunkt orientieren.
Kleine Randbemerkung: Wie man in der Grafik sieht, ist die Wertetabelle von nicht sehr geschickt, weil die x-Werte so gewählt sind, dass der Scheitelpunkt in den berechneten Werten gar nicht enthalten ist. Aus den Werten geht nur der aufsteigende Teil der Parabel hervor, was einen falschen Eindruck vom Verlauf der Funktion erwecken kann. Auch fürs Erstellen von Wertetabellen ist es also gut, aus dem Funktionsterm eine Vorstellung vom Verlauf des Graphen entwickeln zu können. Dann kann man die x-Werte so auswählen, dass sie dem Verlauf des Graphen gerecht werden. In diesem Fall wären x-Werte zwischen
und
besser gewesen.
Zusammenfassung:
Wir sind von der Scheitelpunktform einer Parabel mit
und
ausgegangen und sind über die Beispiele zu folgenden Erkenntnissen gekommen:
bewirkt eine Streckung/Stauchung der Parabel.
führt zu einer Verschiebung der Parabel nach rechts/links.
verschiebt die Parabel nach oben/unten.
Selbstverständlich kann eine Parabel gleichzeitig gestreckt/gestaucht und nach rechts/links und nach oben/unten verschoben sein, z. B. .
Sie ist
Graphisch sieht diese Funktion so aus:
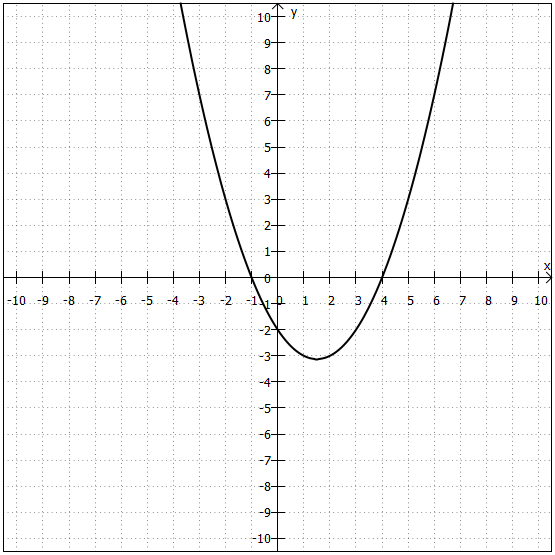
Sowohl aus der Funktionsgleichung als auch aus dem Graphen können Sie ablesen, dass der Scheitelpunkt bei liegt (Achtung: kein Minuszeichen bei der x-Koordinate!). Daher heißt diese Form der Funktionsgleichung Scheitelpunktform. Natürlich kann man den Funktionsterm auch ausmultiplizieren:
Das nennt man die allgemeine Form der Funktionsgleichung. Wenn Sie die Funktion z. B. ableiten möchten (Wir klären in einem späteren Kapitel, was das ist ...), ist die ausmultiplizierte Form der Funktionsgleichung sehr hilfreich. Allerdings ist in ausmultiplizierter Form, also bei , nicht mehr zu erkennen, wo der Scheitelpunkt liegt. Dafür ist - wie der Name schon sagt - die Scheitelpunktform nützlicher. Beide Formen haben also ihre Berechtigung und man muss schauen, in welchem Kontext die quadratische Funktion steht, um zu entscheiden, welche Form benötigt wird.
Unabhängig davon: Achten Sie beim Ausmultiplizieren unbedingt auf die richtige Reihenfolge der Rechenoperationen - Sie wissen ja: Klammern vor Potenz- vor Punkt- vor Strichrechnung! Und die 2. binomische Formel möchte beim Auflösen von auch berücksichtigt werden ...
Quadratische Ergänzung
Gerade habe wir uns angeschaut, wie man in wenigen Schritten von der Scheitelpunktform zur allgemeinen Gleichung einer quadratischen Funktion kommt. Der umgekehrte Weg ist (leider) komplizierter: Das Verfahren dazu heißt quadratische Ergänzung und beruht auf der Anwendung der 1. oder 2. binomischen Formel von rechts nach links. Wir schauen uns das genaue Vorgehen an folgendem Beispiel an:
Jetzt kommt man auf die Idee, den Term innerhalb der Klammer mithilfe der 2. binomischen Formel zusammenzufassen: . Die ersten beiden Summanden passen dafür ja schon gut. Ganz so einfach funktioniert es dann aber doch nicht, da das Quadrieren mit der binomischen Formel eine
als letzten Summanden liefert und nicht eine
. Wir können die
in unserer Funktionsgleichung aber so "zerlegen", dass die benötigte
entsteht und dann noch ein Rest, der uns erst mal nicht weiter kümmert. In diesem Fall ist das
, denn
. Salopp formuliert: Die
ist ein bisschen wie "Wünsch Dir was" und die
der Korrekturterm, damit sich der Term nicht ändert. Das fügt man in die obere Rechnung ein und erhält:
Nun hat man alle drei Summanden zusammen, um die 2. binomische Formel von rechts nach links anwenden zu können. Die letzte in der Funktionsgleichung bleibt dabei einfach stehen:
Jetzt sind wir fertig und können den Scheitelpunkt wie gewohnt ablesen: Er liegt bei .
Weitere interessante Punkte einer Parabel
Nun haben wir schon viel zum Verlauf einer Parabel zusammengetragen. Neben dem Scheitelpunkt gibt es noch weitere interessante Punkte, die über den Verlauf einer Parabel Aufschluss geben. Diese Punkte wollen wir uns zum Abschluss des Kapitels noch kurz anschauen.
Betrachten wir nochmal die Funktion von oben, deren Scheitelpunkt bei
liegt. Wie wir gesehen hatten, schneidet diese Parabel die x-Achse. Solche Schnittpunkte nennt man Nullstellen (Mehr dazu wird es im nächsten Kapitel geben ...). Uns interessiert für den Moment, wie man sie bei quadratischen Funktionen ermittelt: Da der Funktionsgraph bei einer Nullstelle die x-Achse schneidet, muss der zugehörige Funktionswert
sein. Wir müssen also die x-Werte der Funktion berechnen, für die das zutrifft. Man setzt nun
an der Stelle von
in die Funktionsgleichung ein. Das nennt man "die Funktion nullsetzen". Jetzt müssen wir nur noch die entstandene quadratische Gleichung lösen:
Zur Probe setzen wir beide Stellen in ein und berechnen die Funktionswerte.
Für :
Für :
Ergebnis: Beide Funktionswerte sind .
hat also bei
und
Nullstellen.
Nutzen wir gleich noch ein paar Erkenntnisse von den quadratischen Gleichungen und übertragen sie auf Funktionen: Es gibt quadratische Gleichungen, die keine, eine oder zwei Lösungen haben. Das bedeutet für die entsprechenden Funktionen, dass sie keine, eine oder zwei Nullstellen haben. Für alle drei Fälle haben Sie weiter oben in diesem Kapitel schon Beispiele gesehen.
Wie Sie vielleicht gemerkt haben, geht der Wechsel von quadratischen Funktionen zu quadratischen Gleichungen - und auch umgekehrt - manchmal schnell (Die letzte Rechnung könnte Ihnen zumindest teilweise bekannt vorgekommen sein ...). Dieser Zusammenhang zwischen Gleichungen und Funktionen wird Ihnen (auch in diesem Lernmodul) immer wieder begegnen. Das ist eine ziemlich nützliche Eigenschaft, die es ermöglicht, bei vielen Aufgaben von zwei Seiten zu argumentieren: rechnerisch und graphisch. Stimmen dann die rechnerischen und die graphischen Ergebnisse nicht überein, weiß man, dass ein Fehler im Lösungsweg enthalten ist - und kann sich auf die Suche machen, um den Fehler zu finden und die Lösung zu korrigieren.