SOS Mathematik
Übersicht:
17.3 Logarithmusgleichungen und -funktionen - Lösungen
Erste Bemerkung zur Bestimmung des Definitionsbereichs: Auch bei unkomplizierten Logarithmen wie (Aufgabe 1.2) muss im Definitionsbereich berücksichtigt werden, dass das Argument nicht negativ oder
werden darf. Möglich sind in diesem Fall alle positiven reellen Zahlen, also ist
. Da im Fall von
das Argument so einfach ist, wurde dafür in den folgenden Aufgaben keine Rechnung aufgeschrieben.
Um Logarithmen wie (Aufgabe 1.3) oder
(Aufgabe 1.20) müssen wir uns bei der Bestimmung des Definitionsbereichs nicht kümmern, weil
bzw.
einfach Zahlen sind.
Zweite Bemerkung zur Bestimmung des Definitionsbereichs: Da das Argument größer als sein muss, müssen zur Bestimmung des Definitionsbereichs Ungleichungen gelöst werden. Wenn Sie damit Schwierigkeiten haben, schauen Sie bitte im entsprechenden Kapitel nach.
1. Aufgabe
1)
Bestimmung des Definitionsbereichs:
1. Argument links:
2. Argument links:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
2)
Definitionsbereich:
Lösung der Gleichung:
Bemerkung: Die Division durch ist hier ohne Einschränkungen möglich, weil
. Eine Division durch
kann also nicht passieren.
3)
Definitionsbereich:
Lösung der Gleichung:
4)
Bestimmung des Definitionsbereichs:
Argument links:
Argument rechts:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
Bemerkung: Die Multiplikation mit ist hier problemlos möglich, weil
. Eine Multiplikation mit
kann also nicht passieren.
5)
Bestimmung des Definitionsbereichs:
1. Argument links:
2. Argument links:
1. Argument rechts:
Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
Diese Gleichung hat also zwei Lösungen bei und
. Diese x-Werte sind auf jeden Fall nicht Teil des Definitionsbereichs. Es ergeben sich die Intervalle
,
und
.
Jetzt muss noch geprüft werden, in welchen Intervallen der Term positive bzw. negative Werte annimmt. Es ist sinnvoll, für die Prüfung möglichst einfache x-Werte zu verwenden, Z. B. liefert als Ergebnis
, für
ergibt sich
und
führt zu
. Das bedeutet, dass
im ersten und dritten Intervall positiv ist. Die ursprüngliche Ungleichung
ist also nur in diesen beiden Intervallen wahr.
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
Bemerkung: Unabhängig davon, welches Element des Definitionsbereichs in diese Gleichung eingesetzt wird, erhält man immer auf beiden Seiten dasselbe Ergebnis. ist schließlich immer richtig. Jede reelle Zahl löst also diese Gleichung, d. h. die Lösungsmenge entspricht dem Definitionsbereich.
6)
Bestimmung des Definitionsbereichs:
1. Argument links:
2. Argument links:
Da Potenzen mit einer positiven Basis, wie und
, ausschließlich positive Werte annehmen, sind die gegebenen Ungleichungen für alle x-Werte wahr. Der Definitionsbereich ist also
.
Lösung der Gleichung:
7)
Bestimmung des Definitionsbereichs:
1. Argument links:
Da das Argument des ersten Logarithmus eine Quadratwurzel ist und solche Wurzeln ausschließlich nichtnegative Ergebnisse liefern, muss nur vermieden werden, dass die Wurzel den Wert
annimmt:
Radikand im 1. Argument links:
2. Argument links:
Da das Argument des zweiten Logarithmus ein quadratischer Ausdruck ist und Quadrate im Bereich der reellen Zahlen immer nichtnegativ sind, muss nur ausgeschlossen werden, dass das Quadrat den Wert
annimmt:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
8)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Lösung der Gleichung:
9)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Lösung der Gleichung:
Bemerkung: Die Multiplikation mit ist hier ohne Einschränkungen möglich, weil
. Eine Multiplikation mit
kann also nicht passieren.
10)
Bestimmung des Definitionsbereichs:
1. Argument links:
Da ein Quadrat im Bereich der reellen Zahlen immer nichtnegativ ist, muss im vorliegenden Fall nur vermieden werden, dass der quadratische Ausdruck wird:
Argument rechts:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
11)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Lösung der Gleichung:
12)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Lösung der Gleichung:
13)
Bestimmung des Definitionsbereichs:
1. Argument links:
Da das Argument des ersten Logarithmus eine Quadratwurzel ist und solche Wurzeln ausschließlich nichtnegative Ergebnisse liefern, muss nur vermieden werden, dass die Wurzel den Wert
annimmt:
Radikand im 1. Argument links:
2. Argument links:
Da das Argument des zweiten Logarithmus eine 3. Wurzel ist, könnte das Ergebnis der Wurzel auch negativ oder
sein. Um das auszuschließen, muss der Radikand
einen positiven Wert haben. Die zugehörige Ungleichung
wurde aber schon bei der Betrachtung des Radikanden im 1. Argument auf der linken Gleichungsseite gelöst.
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche s-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
Da diese Logarithmusgleichung Wurzeln enthält, muss eine Probe durchgeführt werden:
Es ergibt sich eine wahre Aussage:
14)
Bestimmung des Definitionsbereichs:
1. Argument links:
2. Argument links:
Bemerkung: Durch die Multiplikation mit kann eine Fallunterscheidung bei der Ungleichung vermieden werden, da ein Quadrat im Bereich der reellen Zahlen immer nichtnegativ ist. Somit ist eine Umkehrung des Vergleichszeichens ausgeschlossen.
Argument rechts:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
Bemerkung: Die Division durch ist hier ohne Einschränkungen möglich, weil
. Eine Division durch
kann also nicht passieren.
15)
Bestimmung des Definitionsbereichs:
Argument:
Nenner:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
Bemerkung: Die Multiplikationen mit und
sind hier ohne Einschränkungen möglich, weil
und
. Eine Multiplikation mit
kann also nicht passieren.
16)
Bestimmung des Definitionsbereichs:
Argument links:
Da ein Quadrat im Bereich der reellen Zahlen immer nichtnegativ ist, muss im vorliegenden Fall nur vermieden werden, dass der quadratische Ausdruck wird:
Argument rechts:
Da für schon bei der Betrachtung des linken Arguments ausgeschlossen wurden, dass die Variable den Wert
annimmt, wurde damit auch gleichzeitig sichergestellt, dass im rechten Argument keine Division durch
auftritt.
Bemerkung: Durch die Multiplikation mit kann eine Fallunterscheidung bei der Ungleichung vermieden werden, da ein Quadrat im Bereich der reellen Zahlen immer nichtnegativ ist. Somit ist eine Umkehrung des Vergleichszeichens ausgeschlossen.
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
Bemerkung: Die Multiplikation mit ist hier ohne Einschränkungen möglich, weil
. Eine Multiplikation mit
kann also nicht passieren.
Auch hier muss eine Probe durchgeführt werden, weil in der Gleichung eine Wurzel enthalten ist:
Es ergibt sich eine wahre Aussage:
17)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Lösung der Gleichung:
18)
Bestimmung des Definitionsbereichs:
Argument links:
Da ein Quadrat im Bereich der reellen Zahlen immer nichtnegativ ist, muss im vorliegenden Fall nur vermieden werden, dass der quadratische Ausdruck wird:
Argument rechts:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Lösung der Gleichung:
Da dies ein Widerspruch ist, hat diese Gleichung keine Lösung:
Bemerkung: Die Division durch ist hier ohne Einschränkungen möglich, weil
. Eine Division durch
kann also nicht passieren.
19)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Lösung der Gleichung:
Bemerkung: Die Division durch ist hier ohne Einschränkungen möglich, weil
. Eine Division durch
kann also nicht passieren.
20)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Lösung der Gleichung:
2. Aufgabe
Wie bei den Exponentialfunktionen wurden hier immer nur zwei Graphen in ein Koordinatensystem eingezeichnet und als Orientierung die Funktion (fett gedruckt) mit abgebildet.
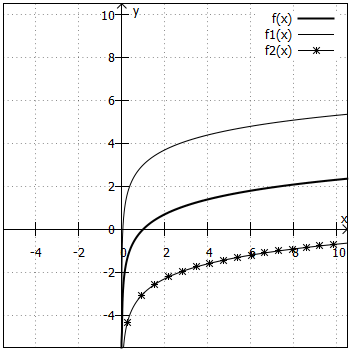
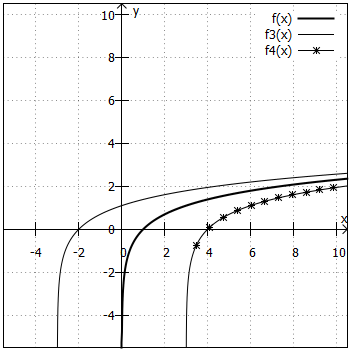
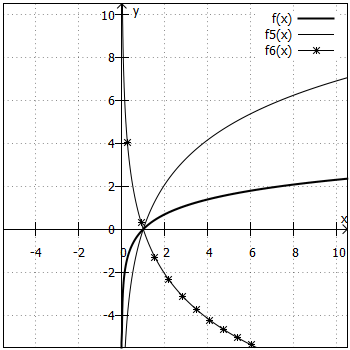
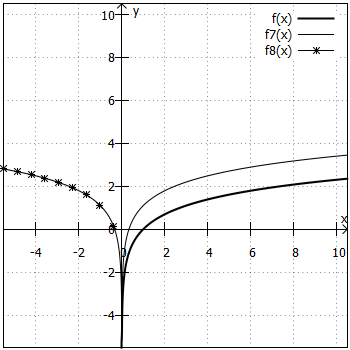
3. Aufgabe
1)
a)
b)
Bemerkung: Schaut man sich die Lösung zu Teil a) genau an, sieht man, dass es sich bei um eine Nullstelle handelt. Da es sich beim Argument des Logarithmus um einen linearen Term handelt, hätte man sich die Rechnung für Teil b) sparen können, da es nur einen Wert für
geben kann, der dazu führt, dass das Argument
und somit der Logarithmus
wird. Die Funktion kann also nur eine Nullstelle haben ...
4. Aufgabe
1)
Bestimmung des Definitionsbereichs:
Da das Argument des Logarithmus ein quadratischer Term ist und Quadrate im Bereich der reellen Zahlen immer nichtnegativ sind, muss nur vermieden werden, dass das Quadrat den Wert
annimmt:
Der Definitionsbereich ist also .
Berechnung der Nullstellen:
Ergebnis: Die Nullstellen von liegen bei
und
.
2)
Bestimmung des Definitionsbereichs:
1. Argument rechts:
2. Argument rechts:
Da das Argument des zweiten Logarithmus ein quadratischer Term ist und Quadrate im Bereich der reellen Zahlen immer nichtnegativ sind, muss nur vermieden werden, dass das Quadrat den Wert
annimmt:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Die einzige Nullstelle von liegt bei
.
3)
Bestimmung des Definitionsbereichs:
Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
Diese Gleichung hat also zwei Lösungen bei und
. Diese x-Werte sind auf jeden Fall nicht Teil des Definitionsbereichs. Es ergeben sich die Intervalle
,
und
.
Jetzt muss noch geprüft werden, in welchen Intervallen der Term positive bzw. negative Werte annimmt. Es ist sinnvoll, für die Prüfung möglichst einfache x-Werte zu verwenden. Z. B. liefert als Ergebnis
, für
ergibt sich
und
führt zu
. Das bedeutet, dass
im ersten und dritten Intervall positiv ist. Die ursprüngliche Ungleichung
ist also nur in diesen beiden Intervallen wahr.
Der Definitionsbereich ist also .
Berechnung der Nullstellen:
Ergebnis: Die Nullstellen von liegen bei
und
.
4)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Berechnung der Nullstellen:
Ergebnis: Die Nullstellen von liegen bei
und
.
5)
Bestimmung des Definitionsbereichs:
Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
Diese Gleichung hat also zwei Lösungen bei und
. Diese x-Werte sind auf jeden Fall nicht Teil des Definitionsbereichs. Es ergeben sich die Intervalle
,
und
.
Jetzt muss noch geprüft werden, in welchen Intervallen der Term positive bzw. negative Werte annimmt. Es ist sinnvoll, für die Prüfung möglichst einfache x-Werte zu verwenden, Z. B. liefert als Ergebnis
, für
ergibt sich
und
führt zu
. Das bedeutet, dass
im ersten und dritten Intervall positiv ist. Die ursprüngliche Ungleichung
ist also nur in diesen beiden Intervallen wahr.
Der Definitionsbereich ist also .
Berechnung der Nullstellen:
Ergebnis: Die Nullstellen von liegen bei
und
.
6)
Bestimmung des Definitionsbereichs:
2. Argument links:
3. Argument links:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist der Fall für . Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Die Nullstelle von liegt bei
.
7)
Bestimmung des Definitionsbereichs:
Da ein Quadrat im Bereich der reellen Zahlen immer nichtnegativ ist, ist das Argument als Summe aus einem Quadrat und der Zahl immer positiv. Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Da im Bereich der reellen Zahlen aus negativen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Funktion keine Nullstellen.
8)
Bestimmung des Definitionsbereichs:
Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Gleichung keine Lösung.
Jetzt muss noch geprüft werden, ob der Term nur positive oder nur negative Werte annimmt. Es ist sinnvoll, für die Prüfung einen möglichst einfachen x-Wert zu verwenden. Z. B. liefert als Ergebnis
. Das bedeutet, dass
für jeden x-Wert positiv ist.
Der Definitionsbereich ist also .
Berechnung der Nullstellen:
Ergebnis: Die Nullstellen von liegen bei
,
und
.
9)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Berechnung der Nullstellen:
Ergebnis: Die Nullstelle von liegt bei
.
10)
Bestimmung des Definitionsbereichs:
1. Argument im Zähler:
Argument in Nenner:
Nenner:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist der Fall für unter Ausschluss der Zahl
. Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Die Nullstelle von liegt bei
.
Bemerkung: Die Multiplikation mit ist hier ohne Einschränkungen möglich, weil
. Eine Multiplikation mit
kann also nicht passieren.
11)
Bestimmung des Definitionsbereichs:
Der Definitionsbereich ist also .
Berechnung der Nullstellen:
Ergebnis: Die Nullstelle von liegt bei
.
12)
Bestimmung des Definitionsbereichs:
Argument:
Nenner:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Die Nullstelle von liegt bei
.
Bemerkung: Die Multiplikation mit ist hier problemlos möglich, weil
und
. Eine Multiplikation mit
kann also nicht passieren.
13)
Bestimmung des Definitionsbereichs:
Nenner des 1. Arguments rechts:
1. Argument rechts:
Hier ist eine Fallunterscheidung nötig, da wir mit der Variablen multiplizieren müssen.
Fall 1: Wir nehmen an, dass ist. Dann muss
sein.
Im Abgleich zwischen Eintrittsbedingung und Lösung des 1. Falls ergibt sich folgendes Zwischenergebnis:
Fall 2: Wir nehmen an, dass ist. Dann muss
sein.
Im Abgleich zwischen Eintrittsbedingung und Lösung des 2. Falls ergibt sich folgendes Zwischenergebnis:
Die Fallunterscheidung liefert uns also oder
.
Nenner des 2. Arguments rechts:
2. Argument rechts:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Die Nullstelle von liegt bei
und
.
Bemerkung: Die Multiplikation mit ist hier ohne Einschränkungen möglich, weil
. Eine Multiplikation mit
kann also nicht passieren.
14)
Bestimmung des Definitionsbereichs:
1. Argument links:
2. Argument links:
Ein Bruch ist genau dann positiv, wenn Zähler und Nenner das gleiche Vorzeichen besitzen. Das beinhaltet, dass weder Zähler noch Nenner sein dürfen.
In diesem Funktionsterm steht im Zähler ein Quadrat. Da ein Quadrat im Bereich der reellen Zahlen immer nichtnegativ ist, muss nur vermieden werden, dass das Quadrat den Wert annimmt:
Damit der gesamte Bruch einen positiven Wert annimmt, muss also auch der Nenner positiv sein. Die zugehörige Ungleichung wurde aber schon bei der Betrachtung des 1. Arguments auf der linken Gleichungsseite gelöst.
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Die Nullstelle von liegt bei
.
15)
Bestimmung des Definitionsbereichs:
1. Argument rechts:
Da das Argument des ersten Logarithmus ein Produkt aus einer positiven Zahl und einem Quadrat ist und solche Terme ausschließlich nichtnegative Ergebnisse liefern, muss nur vermieden werden, dass der Term den Wert annimmt:
2. Argument rechts:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Die Nullstelle von liegt bei
.
16)
Bestimmung des Definitionsbereichs:
Argument im Zähler:
Nenner:
Argument im Nenner:
Die zugehörige Ungleichung wurde schon bei der Betrachtung des Arguments im Zähler gelöst.
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für unter Ausschluss der Zahl
. Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Die Nullstellen von liegen bei
und
.
17)
Bestimmung des Definitionsbereichs:
Um diese quadratische Ungleichung zu lösen, wird im ersten Schritt die zugehörige quadratische Gleichung gelöst:
Diese Gleichung hat also zwei Lösungen bei und
. Diese x-Werte sind auf jeden Fall nicht Teil des Definitionsbereichs. Es ergeben sich die Intervalle
,
und
.
Jetzt muss noch geprüft werden, in welchen Intervallen der Term positive bzw. negative Werte annimmt. Es ist sinnvoll, für die Prüfung möglichst einfache x-Werte zu verwenden. Z. B. liefert als Ergebnis
, für
ergibt sich
und
führt zu
. Das bedeutet, dass der Term
im ersten und dritten Intervall positiv ist. Die ursprüngliche Ungleichung
ist also nur in diesen beiden Intervallen wahr.
Der Definitionsbereich ist also
Berechnung der Nullstellen:
Ergebnis: Die Nullstellen von liegen bei
und
.
18)
Bestimmung des Definitionsbereichs:
Da Potenzen mit geraden Exponenten im Bereich der reellen Zahlen immer nichtnegativ sind, ist das Argument als Summe aus solchen Potenzen und der Zahl immer positiv. Somit kann die gegebene Ungleichung niemals wahr werden. Der Definitionsbereich ist also
.
Da diese Funktion für keine Werte definiert ist, erübrigt sich die Suche nach Nullstellen.
19)
Bestimmung des Definitionsbereichs:
1. Argument rechts:
Da Potenzen mit einer positiven Basis, wie , ausschließlich positive Werte annehmen, ist die gegebene Ungleichung für alle x-Werte wahr.
2. Argument rechts:
Der Definitionsbereich ist also .
Berechnung der Nullstellen:
Ergebnis: Da der Logarithmus von nicht definiert ist, liegt die einzige Nullstelle von
bei
.
20)
Bestimmung des Definitionsbereichs:
1. Argument rechts:
2. Argument rechts:
Für die abschließende Ermittlung des Definitionsbereichs muss nun überprüft werden, für welche x-Werte alle ermittelten Bedingungen erfüllt sind. Das ist nur der Fall für . Der Definitionsbereich ist also
.
Berechnung der Nullstellen:
Ergebnis: Die Nullstellen von liegen bei
und
.