SOS Mathematik
Übersicht:
- Lösung zur 1. Aufgabe
- Lösung zur 2. Aufgabe
- Lösung zur 3. Aufgabe
- Lösung zur 4. Aufgabe
- Lösung zur 5. Aufgabe
13.3 Polynomgleichungen und -funktionen - Lösungen
1. Aufgabe
1) Grad
2) Grad
3) Grad
4) Grad
5) Grad
6) Grad
Bemerkung: Der Grad ist hier und nicht
, weil
den Koeffizienten
hat.
7) Grad
8) Grad
9) Grad
10) Grad
2. Aufgabe
2)
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Gleichung keine Lösung:
3)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
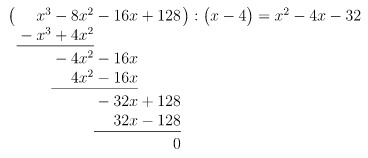
Lösung des reduzierten Polynoms:
4)
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert der zweite Faktor keine weiteren Lösungen:
5)
Substitution:
Rücksubstitution:
6)
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert der erste Faktor keine weiteren Lösungen:
7)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
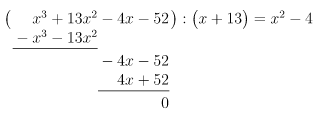
Lösung des reduzierten Polynoms:
8)
Substitution:
Rücksubstitution:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert der zweite Faktor keine weiteren Lösungen:
10)
Bemerkung: Unabhängig davon, welches Element des Definitionsbereichs in diese Gleichung eingesetzt wird, erhält man immer auf beiden Seiten dasselbe Ergebnis. ist schließlich immer richtig. Jede reelle Zahl löst also diese Gleichung, d. h. die Lösungsmenge entspricht dem Definitionsbereich.
11)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
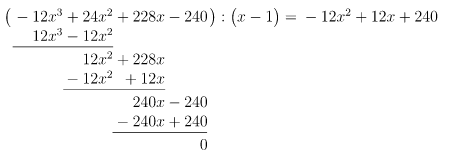
Lösung des reduzierten Polynoms:
12)
Substitution:
Rücksubstitution:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert die Rücksubstitution von keine weiteren Lösungen:
14)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
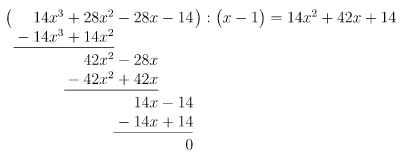
Lösung des reduzierten Polynoms:
17)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
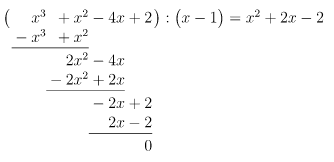
Lösung des reduzierten Polynoms:
18)
Alternativer Lösungsweg:
Man könnte als Alternative zu dem Lösungsweg oben auf die Idee kommen, die Gleichung durch zu teilen. Schließlich ist
auf beiden Seiten der Gleichung als Faktor enthalten. Allerdings ist dann eine Fallunterscheidung nötig, da wir durch die Variable dividieren.
1. Fall: Wir nehmen an, dass ist. Das bedeutet, dass
ist:
In diesem Fall dürfen wir durch teilen. Eine Division durch
ist ja ausgeschlossen.
Nun müssen wir noch die beiden errechneten Werte mit der Eintrittsbedingung abgleichen: und
. Geht also beides in Ordnung.
2. Fall: Wir nehmen an, dass , also
ist:
In diesem Fall dürfen wir nicht durch teilen, da wir dann durch
dividieren würden. Ersetzen wir in der Gleichung
durch
, erhalten wir
Dies ist eine wahre Aussage. Das heißt, erfüllt die Gleichung ebenfalls. Wir haben also eine weitere Lösung gefunden.
Lösung: Die Lösungsmenge besteht aus den Lösungen beider Fälle:
Bemerkung: Sie sehen an diesem Beispiel, dass es keine gute Idee wäre, nur durch zu dividieren, ohne die beiden entstehenden Fälle zu unterscheiden. Dann würden wir nämlich die Lösung
"verlieren".
19)
Für welche Werte des Parameters sind diese Werte Lösungen der Gleichung? Dazu müssen wir schauen, was im Radikanden passiert. Der darf ja nun mal nicht kleiner als
sein ... Hier haben wir keine Probleme:
ist positiv,
ist nichtnegativ, beides wird addiert. Bleibt also positiv.
sind also ohne Einschränkung Lösungen der Gleichung.
Bevor wir an dieser Stelle durch teilen, müssen wir eine Fallunterscheidung vornehmen, weil wir nicht wissen, welchen Wert
annimmt.
könnte ja
sein.
1. Fall: Wir nehmen an, dass ist. Anders formuliert: Wir nehmen an, dass
ist:
In diesem Fall dürfen wir durch teilen. Eine Division durch
ist ja ausgeschlossen.
Jetzt müssen wir noch prüfen, für welche Werte von der Radikand nichtnegativ ist:
Nun müssen wir noch die Eingangsbedingung der Fallunterscheidung mit der errechneten Bedingung abgleichen: Die Werte sind dann Lösungen, wenn der Parameter
, aber
ist.
2. Fall: Wir nehmen an, dass ist. Also ist der Parameter
. Dann erhalten wir in der Gleichung:
In diesem Fall, also wenn ist, löst jede reelle Zahl diese Gleichung, d. h. die Lösungsmenge entspricht dem Definitionsbereich.
ist schließlich immer richtig.
Zusammenfassung der Lösung, abhängig vom Wert des Parameters :
Für und
ist
.
Für ist
.
Für ist
.
Bemerkung: Die Lösungen, die sich bei "Faktor 1" ergeben haben, nicht vergessen!
20)
Das ist aber nicht die vollständige Lösung der Gleichung. Warum nicht? Wenn man durch dividiert, muss man natürlich sicher sein, dass der Term ungleich
ist, da man durch
ja nun mal nicht teilen darf. Darum müssen wir uns jetzt noch kümmern:
Eine Potenz wie kann grundsätzlich nur dann
sein, wenn die Basis
ist. Für
ist auch
, egal welchen Wert
annimmt. Der einzige "Sonderfall" wäre, wenn sowohl Basis als auch Exponent
wären. Der Exponent
ist
, wenn
ist. Das kann also nicht passieren. Trotzdem haben wir den Fall
mit der Rechnung oben noch nicht abgedeckt und müssen jetzt noch schauen, was dabei passiert:
Das ist eine wahre Aussage. ist also auch Lösung der Gleichung.
Insgesamt ergibt sich folgende Lösungsmenge:
3. Aufgabe
Zu den Eigenschaften, die in diesen Zusammenhang interessieren, zählen: Achsen- bzw. Punktsymmetrie, das Randverhalten, die mögliche Anzahl von Nullstellen, Extrempunkten und Wende- bzw. Sattelpunkten etc.
Um einen Funktionsgraphen zu zeichen, kann zusätzlich eine Wertetabelle helfen. Diese sind in der Musterlösung nicht angegeben.
Bemerkung: Achten Sie jeweils auf die Skaleneinteilung der Koordinatensysteme! Diese sollte immer so gewählt werden, dass der charakteristische Teil des Graphen dargestellt wird. Dort, wo es sinnvoll ist, sind die Funktionen in den folgenden Aufgaben doppelt dargestellt - einmal in einem Koordinatensystem, in dem die Achsen jeweils den Zahlenbereich von bis
umfassen (zur besseren Vergleichbarkeit), und einmal mit einer auf die Funktion angepassten Achseneinteilung.
1)
Symmetrie: Als Polynom, das sowohl gerade als auch ungerade Exponenten enthält, ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Koordinatenursprung.
Randverhalten: Als Polynom ungeraden Grades, bei dem die höchste Potenz einen negativen Koeffizienten hat, sind die Funktionswerte bei sehr kleinen x-Werten sehr groß und bei sehr großen x-Werten sehr klein.
Nullstellen: Als Polynom ungeraden Grades hat mindestens eine Nullstelle. Maximal kann es drei Nullstellen geben.
Extrempunkte: kann maximal zwei Extrempunkte haben.
Wende- und Sattelpunkte: Als Polynom ungeraden Grades mit dem Grad hat
genau einen Wende- bzw. Sattelpunkt.
Sonstiges: Die Funktion schneidet die y-Achse im Punkt .

2)
Symmetrie: Als Polynom, das sowohl gerade als auch ungerade Exponenten enthält, ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Koordinatenursprung. Wenn man nur die Zeichnung betrachtet, könnte man denken, dass die Funktion achsensymmetrisch zur y-Achse ist. Man muss wirklich genau schauen (vor allem, wenn die Skaleneinteilung an den Achsen nicht optimal gewählt wurde), um zu erkennen, dass dem nicht so ist. Deswegen ist eine rechnerische oder argumentative Lösung in vielen Fällen besser als eine zeichnerische.
Randverhalten: Als Polynom geraden Grades, bei dem die höchste Potenz einen positiven Koeffizienten hat, sind die Funktionswerte sowohl bei sehr kleinen als auch bei sehr großen x-Werten sehr groß.
Nullstellen: Als Polynom ohne konstanten Term hat mindestens eine Nullstelle bei
. Maximal kann es vier Nullstellen geben.
Extrempunkte: Als Polynom geraden Grades hat mindestens einen Extrempunkt. Maximal kann es drei Extrempunkte geben.
Wende- und Sattelpunkte: kann maximal zwei Wende- bzw. Sattelpunkte haben.
Sonstiges: Die Funktion schneidet die y-Achse im Punkt .
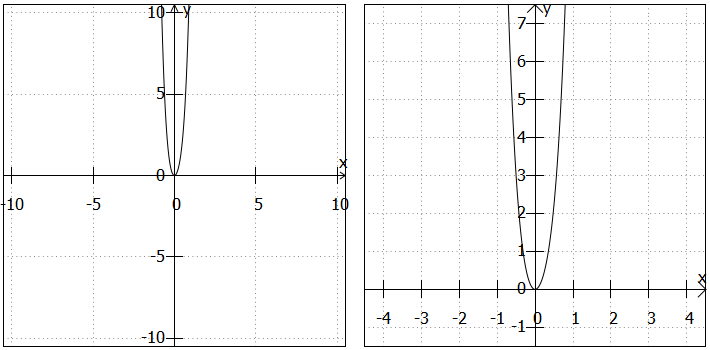
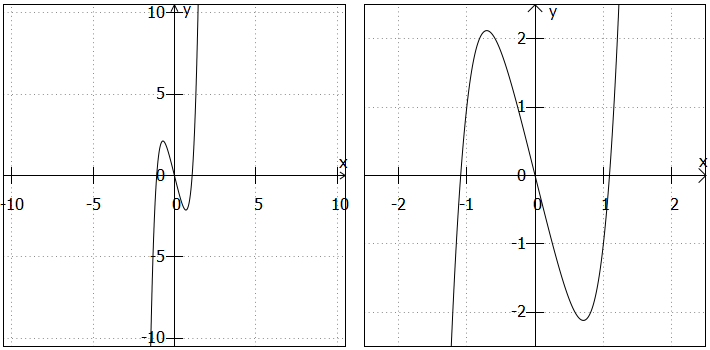
3)
Symmetrie: Als Polynom, das nur gerade Exponenten enthält, ist achsensymmetrisch zur y-Achse.
Randverhalten: Als Polynom geraden Grades, bei dem die höchste Potenz einen positiven Koeffizienten hat, sind die Funktionswerte sowohl bei sehr kleinen als auch bei sehr großen x-Werten sehr groß.
Nullstellen: kann maximal vier Nullstellen haben.
Extrempunkte: Als Polynom geraden Grades hat mindestens einen Extrempunkt. Maximal kann es drei Extrempunkte geben.
Wende- und Sattelpunkte: kann maximal zwei Wende- bzw. Sattelpunkte haben.
Sonstiges: Die Funktion schneidet die y-Achse im Punkt . Deshalb und weil die Parabel nach oben geöffnet ist (der Koeffizient vor
ist positiv), muss es mindestens zwei Nullstellen geben. Vom Punkt
ausgehend schneidet der Graph die x-Achse nämlich einmal im positiven und einmal im negativen Bereich. Weiter kann man argumentieren, dass es nicht drei Nullstellen geben kann, weil die Funktion dann nicht achsensymmetrisch zur y-Achse wäre. Drei Nullstellen und Achsensymmetrie zur y-Achse gemeinsam sind nur dann möglich, wenn eine Nullstelle im Punkt
liegt. Der Punkt
kann aber nicht Teil des Graphen sein, wenn der Punkt
auf dem Graphen liegt.
Bemerkung: Wenn Sie sich die Argumentation zur Anzahl der Nullstellen veranschaulichen wollen, können viele kleine Skizzen helfen. Z. B. können Sie in einem Koordinatensystem den Punkt markieren und dann versuchen Graphen zu zeichnen, die zwei, drei oder vier Nullstellen haben und den übrigen Kriterien entsprechen, also achsensymmetrisch zur y-Achse bzw. nach oben geöffnet sind.
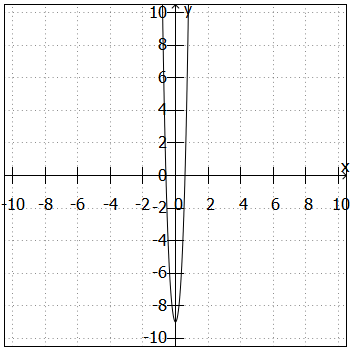
4)
Symmetrie: Als Polynom, das nur ungerade Exponenten enthält, ist punktsymmetrisch zum Koordinatenursprung.
Randverhalten: Als Polynom ungeraden Grades, bei dem die höchste Potenz einen positiven Koeffizienten hat, sind die Funktionswerte bei sehr kleinen x-Werten auch sehr klein und bei sehr großen x-Werten sehr groß.
Nullstellen: Als Polynom ohne konstanten Term hat mindestens eine Nullstelle bei
. Maximal kann es fünf Nullstellen geben.
Extrempunkte: kann maximal vier Extrempunkte haben.
Wende- und Sattelpunkte: Als Polynom ungeraden Grades hat mindestens einen Wende- bzw. Sattelpunkt. Maximal kann es drei Wende- bzw. Sattelpunkte geben.
Sonstiges: Die Funktion schneidet die y-Achse im Punkt .
5)
Symmetrie: Als Polynom, das nur gerade Exponenten enthält, ist achsensymmetrisch zur y-Achse.
Randverhalten: Als Polynom geraden Grades, bei dem die höchste Potenz einen negativen Koeffizienten hat, sind die Funktionswerte sowohl bei sehr kleinen als auch bei sehr großen x-Werten sehr klein.
Nullstellen: kann maximal sechs Nullstellen haben.
Extrempunkte: Als Polynom geraden Grades hat mindestens einen Extrempunkt. Maximal kann es fünf Extrempunkte geben.
Wende- und Sattelpunkte: kann maximal vier Wende- bzw. Sattelpunkte haben.
Sonstiges: Die Funktion schneidet die y-Achse im Punkt . Deshalb und weil die Parabel nach unten geöffnet ist (der Koeffizient vor
ist negativ), muss es folglich mindestens zwei Nullstellen geben. Weiter kann man argumentieren, dass es nicht drei oder fünf Nullstellen geben kann, weil die Funktion dann nicht achsensymmetrisch zur y-Achse wäre. Eine ungerade Anzahl Nullstellen und Achsensymmetrie zur y-Achse gemeinsam sind nur dann möglich, wenn eine Nullstelle im Punkt
liegt. Der Punkt
kann aber nicht Teil des Graphen sein, wenn der Punkt
auf dem Graph liegt.
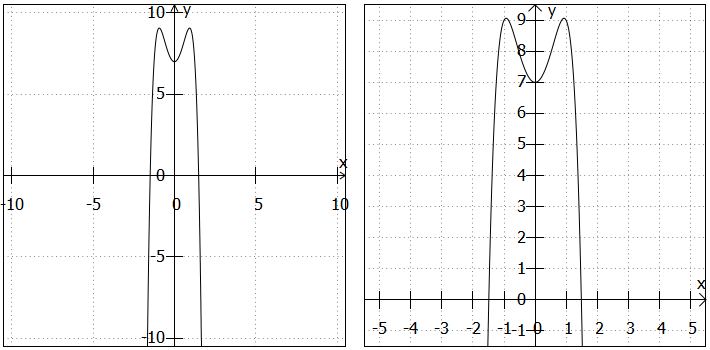
4. Aufgabe
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert der zweite Faktor keine weiteren Punkte.
3)
a)
b)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :

Lösung des reduziertes Polynom mit der p-q-Formel:
4)
a)
b)
Substitution:
Rücksubstitution:
Infos zu stehen unter "allgemeinere Erkenntnisse zu Wurzeln"
7)
a)
b)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
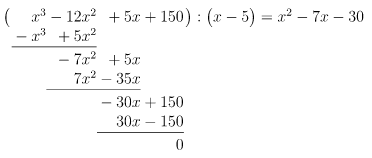
Lösung des reduziertes Polynom mit der p-q-Formel:
9)
a)
b)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
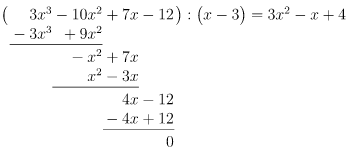
Lösung des reduziertes Polynom mit der p-q-Formel:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, hat diese Gleichung keine weiteren Lösungen. Die Funktion nimmt den Funktionswert also nur bei
an.
10)
a)
b)
Substitution:
Rücksubstitution:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert die Rücksubstitution von keine weiteren Punkte.
5. Aufgabe
1)
Substitution:
Rücksubstitution:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert die Rücksubstitution von keine weiteren Lösungen:
3)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
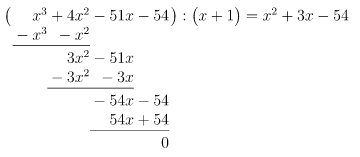
Lösung des reduzierten Polynoms:
4)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :

Lösung des reduzierten Polynoms:
5)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
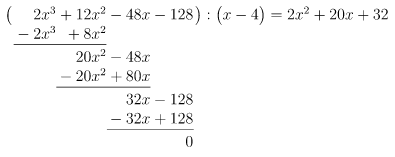
Lösung des reduzierten Polynoms:
6)
Substitution:
Rücksubstitution:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert die Rücksubstitution von keine weiteren Lösungen:
8)
Substitution:
Rücksubstitution:
10)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
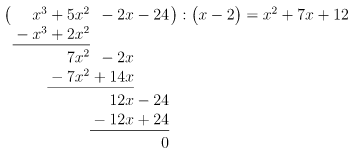
Lösung des reduzierten Polynoms:
11)
Substitution:
Rücksubstitution:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefern der erste Faktor und die Rücksubstitution von keine weiteren Lösungen:
13)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :

Lösung des reduzierten Polynoms:
14)
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert der zweite Faktor keine weiteren Lösungen:
15)
Durch Probieren finden wir die Lösungen und
, denn
und
Polynomdivision mit und
, also mit
:
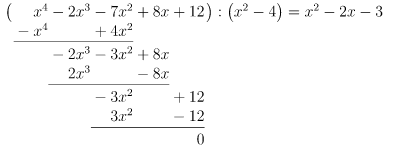
Lösung des reduzierten Polynoms:
16)
Substitution:
Rücksubstitution:
17)
Substitution:
Rücksubstitution:
18)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
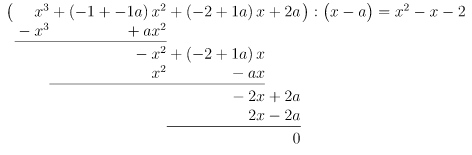
Lösung des reduzierten Polynoms:
19)
Durch Probieren finden wir die Lösung , denn
Polynomdivision mit :
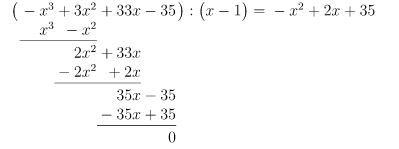
Lösung des reduzierten Polynoms:
20)
Substitution:
Rücksubstitution:
Da aus negativen reellen Zahlen keine Wurzeln mit geraden Wurzelexponenten gezogen werden können, liefert der zweite Faktor keine weiteren Lösungen: