Übersicht:

• Lösung zur 1. Aufgabe
• Lösung zur 2. Aufgabe
• Lösung zur 3. Aufgabe
• Lösung zur 4. Aufgabe
• Lösung zur 5. Aufgabe
• Lösung zur 6. Aufgabe
• Lösung zur 7. Aufgabe
• Lösung zur 8. Aufgabe

22.3 Ableitungen - Lösungen

1. Aufgabe

Um den Verlauf der Ableitung zu der gegebenen Funktion $f(x)$ zu ermitteln, muss die Steigung der Funktion ermittelt werden. In der nachfolgenden Grafik wurde an verschiedenen Stellen die entsprechende Tangente eingezeichnet, mit deren Hilfe man sich die Steigung der Funktion in diesen Punkten verdeutlichen kann:

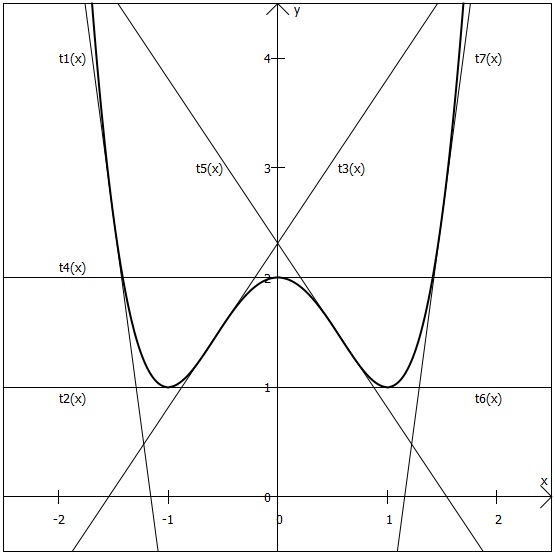
Da es bei dieser Aufgabe nur das Ziel ist, die Größenordnung der Steigung an einer bestimmten Stelle im Vergleich zu anderen einzuschätzen, müssen keine konkreten Zahlenwerte für die Tangentensteigungen ausgerechnet werden. Das geht mit den gegebenen Informationen auch gar nicht ...

Überlegungen zu den Tangenten:

• Die Tangente $t1(x)$ berührt die Funktion im Punkt $\left(-\frac{3}{2} \mid f\left(-\frac{3}{2}\right)\right)$ und ist eine fallende Gerade. Die Steigung von $f(x)$ muss an dieser Stelle also negativ sein.
• Die Tangente $t2(x)$ berührt die Funktion im Punkt $(-1 \mid f(-1))$ und ist eine konstante Gerade. Die Steigung von $f(x)$ muss an dieser Stelle also $0$ sein.
• Die Tangente $t3(x)$ berührt die Funktion im Punkt $\left(-\frac{1}{2} \mid f\left(-\frac{1}{2}\right)\right)$ und ist eine steigende Gerade. Die Steigung von $f(x)$ muss an dieser Stelle also positiv sein.
• Die Tangente $t4(x)$ berührt die Funktion im Punkt $(0 \mid f(0))$ und ist eine konstante Gerade. Die Steigung von $f(x)$ muss an dieser Stelle also $0$ sein.
• Die Tangente $t5(x)$ berührt die Funktion im Punkt $\left(\frac{1}{2} \mid f\left(\frac{1}{2}\right)\right)$ und ist eine fallende Gerade. Die Steigung von $f(x)$ muss an dieser Stelle also negativ sein.
• Die Tangente $t6(x)$ berührt die Funktion im Punkt $(1 \mid f(1))$ und ist eine konstante Gerade. Die Steigung von $f(x)$ muss an dieser Stelle also $0$ sein.
• Die Tangente $t7(x)$ berührt die Funktion im Punkt $\left(\frac{3}{2} \mid f\left(\frac{3}{2}\right)\right)$ und ist eine steigende Gerade. Die Steigung von $f(x)$ muss an dieser Stelle also positiv sein.

• Vergleicht man die beiden fallenden Tangenten $t1(x)$ und $t5(x)$, stellt man fest, dass $t1(x)$ sehr viel steiler verläuft als $t5(x)$. Die Steigung von $t1(x)$ muss als vom Betrag her größer sein als die Steigung von $t5(x)$.
• Gleiches gilt für die beiden steigenden Tangenten $t3(x)$ und $t7(x)$. $t7(x)$ verläuft deutlich steiler als $t3(x)$. Die Steigung von $t7(x)$ muss also vom Betrag her größer sein als die Steigung von $t3(x)$.

Überträgt man diese Erkenntnisse in ein Koordinatensystem, erhält man eine Kurve ähnlich der in der nachfolgenden Grafik gezeigten:

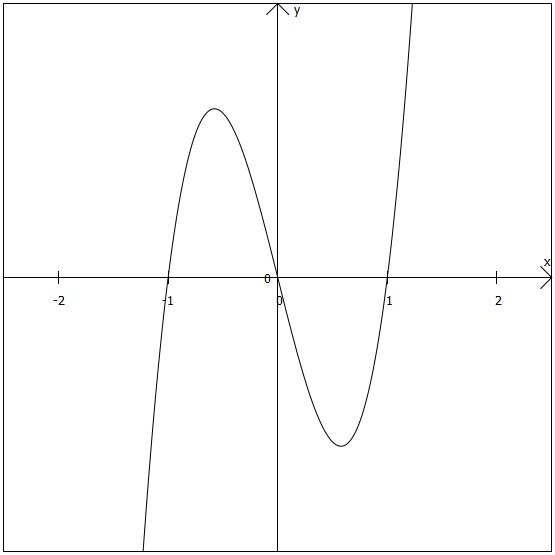
Mehr ist nicht gefragt ...
Diese Aufgabe ist deswegen wichtig, weil Sie sich hierüber einen anderen Blick auf Ableitungen erarbeiten. Dieser hilft zum Beispiel, um berechnete Ableitungen zu überprüfen, aber auch im Kontext von Anwendungsaufgaben.

2. Aufgabe

Bemerkung 1: Bitte denken Sie daran, dass die Rechenregeln, die Sie bislang in diesem Lernmodul gelernt haben, auch im Zusammenhang mit Ableitungen gelten! Das gilt zum Beispiel für folgende Regeln:

• Bruchrechenregeln gelten auch dann, wenn die Brüche innerhalb von Potenzen auftauchen! Beispielsweise muss im Exponenten bei Aufgaben 9) folgendermaßen gerechnet werden: $\frac{1}{3}-1=\frac{1}{3}-\frac{3}{3}=\frac{1-3}{3}=-\frac{2}{3}$, also erst die Brüche gleichnamig machen und dann zusammenfassen.
• Auch die Festlegungen im Rahmen der Potenz- und Wurzelrechnung, also $x^0 = 1$, $\dfrac{1}{x^n}=x^{-n}$ sowie $\sqrt[n]{x}=x^{\frac{1}{n}}$, werden hier immer wieder benötigt.

Bemerkung 2: Die Konstanten-, Faktor- und Summenregel beim Ableiten sind nicht übermäßig überraschend und auch nicht sehr schwierig in der Anwendung. (Vermutlich würden viele intuitiv genauso vorgehen ...) In dieser Aufgabe wird trotzdem Wert auf genau diese einfachen Regeln gelegt, da man sich diese einmal bewusst gemacht haben sollte, damit man später die komplexeren Regeln sinnvoll davon abgrenzen kann.

Bemerkung 3: Ganz so ausführlich wie in dieser Aufgabe müssen Lösungen normalerweise nicht aufgeschrieben werden.

1)
$\begin{array}{rcl} \mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& 8 \cdot 2 \cdot x^{2-1}-0 \cr &=& 16x \end{array}$

Vorgehen: Konstanten-, Faktor-, Summen- und Potenzregel
 

2)
$\begin{array}{rcl}\mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& -10 \cdot 3 \cdot x^{3-1}- 2 \cdot x^{2-1} \cr &=& -30x^2-2x \end{array}$

Vorgehen: Faktor-, Summen- und Potenzregel
 

3)
$\begin{array}{rcl} \mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& -\dfrac{10}{9} \cdot 18 \cdot x^{18-1}-11 \cdot 1 \cdot x^{1-1} \cr &=& -20x^{17}-11 \end{array}$

Vorgehen: Faktor-, Summen- und Potenzregel
 

4)
$\begin{array}{rcl}\mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& 2 \cdot 2 \cdot x^{2-1}-1 \cdot 1 \cdot x^{1-1}-0 \cr &=& 4x-1 \end{array}$

Vorgehen: Konstanten-, Faktor-, Summen- und Potenzregel
 

5)
$\begin{array}{rcl}\mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& -3 \cdot 4 \cdot x^{4-1}+16 \cdot 2 \cdot x^{2-1}+0 \cr &=& -12x^3+32x \end{array}$

Vorgehen: Konstanten-, Faktor-, Summen- und Potenzregel

6)
$\begin{array}{rcl} \mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& \dfrac{1}{4} \cdot 4 \cdot x^{4-1}-\dfrac{1}{3} \cdot 3 \cdot x^{3-1}+ \dfrac{1}{2} \cdot 2 \cdot x^{2-1}-1 \cdot 1 \cdot x^{1-1}+0 \cr &=& x^3-x^2+x-1 \end{array}$

Vorgehen: Konstanten-, Faktor-, Summen- und Potenzregel
 

7)
$\begin{array}{rcl}\mathbb{D} &=& \mathbb{R} \cr\cr f(x) &=& \dfrac{2}{7}x^{14} \cr \cr \cr f'(x) &=& \dfrac{2}{7} \cdot 14 \cdot x^{14-1} \cr\cr &=& 4x^{13} \end{array}$

Vorgehen: Faktor- und Potenzregel
 

8)
$\begin{array}{rcl}\mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& 230 \cdot 12 \cdot x^{12-1} + 17 \cdot 6 \cdot x^{6-1} -\dfrac{3}{5}\cdot 5 \cdot x^{5-1}+0 \cr &=& 2.760x^{11}+102x^5-3x^4 \end{array}$

Vorgehen: Konstanten-, Faktor-, Summen- und Potenzregel

9)
$\begin{array}{rcl}\mathbb{D}&=&]0;\infty[ \cr\cr f'(x) &=& 25 \cdot 4 \cdot x^{4-1} -66 \cdot \dfrac{1}{3} \cdot x^{\frac{1}{3}-1}-17\cdot \dfrac{3}{2} \cdot x^{\frac{3}{2}-1} +0 \cr \cr &=& 100x^3-22x^{-\frac{2}{3}}-\dfrac{51}{2}x^{\frac{1}{2}} \cr \cr &=& 100x^3-\dfrac{22}{\sqrt[3]{x^2}}-\dfrac{51}{2}\sqrt{x} \end{array}$

Vorgehen: Konstanten-, Faktor-, Summen- und Potenzregel

Bemerkung: $e$ ist einfach nur eine Zahl und fällt daher beim Ableiten weg ...

10)
$\begin{array}{rcl}\mathbb{D} &=& \mathbb{R}\setminus_{\{0\}} \cr\cr f'(x) &=& -3 \cdot x^{-3-1}+0 \cr &=& -3x^{-4} \cr \cr &=& -\dfrac{3}{x^4} \end{array}$

Vorgehen: Konstanten-, Summen- und Potenzregel

11)
$\begin{array}{rcl}\mathbb{D}&=&\mathbb{R}\setminus_{\{0\}} \cr \cr f(x) &=& 6x^{-1} \cr \cr \cr f'(x) &=& 6 \cdot \left(-1 \right) \cdot x^{-1-1} \cr &=& -6x^{-2} \cr \cr &=& -\dfrac{6}{x^2} \end{array}$

Vorgehen: Faktor- und Potenzregel

12)
$\begin{array}{rcl}\mathbb{D}&=&]0;\infty[ \cr \cr f(x) &=& 3x^{\frac{1}{2}}-7 \cr \cr \cr f'(x) &=& 3 \cdot \dfrac{1}{2} \cdot x^{\frac{1}{2}-1}-0 \cr \cr &=& \dfrac{3}{2} \cdot x^{-\frac{1}{2}} \cr \cr &=& \dfrac{3}{2} \cdot \dfrac{1}{x^\frac{1}{2}} \cr \cr &=& \dfrac{3}{2\sqrt{x}}\end{array}$

Vorgehen: Konstanten-, Faktor-, Summen- und Potenzregel
 

13)
$\begin{array}{rcl}\mathbb{D}&=&[0;\infty[ \cr \cr f(x) &=& x^1 \cdot x^{\frac{1}{2}} \cr \cr &=& x^{\frac{3}{2}} \cr \cr \cr f'(x) &=& \dfrac{3}{2} \cdot x^{\frac{3}{2}-1} \cr \cr &=& \dfrac{3}{2}x^{\frac{1}{2}} \cr \cr &=& \dfrac{3}{2}\sqrt{x}\end{array}$

Vorgehen: Potenzregel

Bemerkung: Meist lohnt es sich, die Funktion vor dem Ableiten genau zu betrachten und in eine möglichst "geschickte" Form zu bringen, auch wenn es erstmal nach mehr Arbeit aussieht ...
 

14)
$\begin{array}{rcl}\mathbb{D}&=&\mathbb{R}\setminus_{\{0\}} \cr \cr f(x) &=& x^{-2} \cr \cr \cr f'(x) &=& -2 \cdot x^{-2-1} \cr &=& -2\cdot x^{-3} \cr \cr &=& -\dfrac{2}{x^3} \end{array}$

Vorgehen: Potenzregel
 

15)
$\begin{array}{rcl}\mathbb{D}&=&\mathbb{R}\setminus_{\{0\}} \cr \cr f(x) &=& -\dfrac{1}{12} \cdot x^{-3} \cr\cr\cr f'(x) &=& -\dfrac{1}{12} \cdot \left(-3\right) \cdot x^{-3-1} \cr\cr &=& \dfrac{1}{4}x^{-4} \cr\cr &=& \dfrac{1}{4x^4} \end{array}$

Vorgehen: Faktor- und Potenzregel

16)
$\begin{array}{rcl}\mathbb{D}&=&\mathbb{R}\setminus_{\{0\}} \cr \cr f(x) &=& -17x^{-19} \cr \cr \cr f'(x) &=& -17 \cdot \left(-19 \right) \cdot x^{-19-1} \cr &=& 323x^{-20} \cr \cr &=& \dfrac{323}{x^{20}} \end{array}$

Vorgehen: Faktor- und Potenzregel

17)
$\begin{array}{rcl}\mathbb{D}&=&]0;\infty[ \cr \cr f(x) &=&5\cdot x^{\frac{1}{4}}-x+1 \cr\cr\cr f'(x) &=& 5\cdot \dfrac{1}{4} \cdot x^{\frac{1}{4}-1}-1 \cdot x^{1-1}+0 \cr\cr &=& \dfrac{5}{4} \cdot x^{-\frac{3}{4}}-1 \cr\cr &=& \dfrac{5}{4\sqrt[4]{x^3}}-1 \end{array}$

Vorgehen: Konstanten-, Faktor-, Summen- und Potenzregel

18)
$\begin{array}{rcl}\mathbb{D}&=&]0;+\infty[ \cr \cr f(x) &=& \dfrac{1}{6} \cdot x^{-\frac{1}{2}} \cr\cr\cr f'(x) &=& \dfrac{1}{6} \cdot \left(-\dfrac{1}{2}\right) \cdot x^{-\frac{1}{2}-1} \cr\cr &=& -\dfrac{1}{12} \cdot x^{-\frac{3}{2}} \cr\cr &=& -\dfrac{1}{12} \dfrac{1}{\sqrt{x^3}} \cr\cr &=& -\dfrac{1}{12\sqrt{x^3}} \end{array}$

Vorgehen: Faktor- und Potenzregel
 

19)
$\begin{array}{rcl}\mathbb{D}&=&\mathbb{R}\setminus_{\{0\}} \cr \cr f(x) &=& 15 \cdot x^{-\frac{6}{5}} \cr \cr \cr f'(x) &=& 15 \cdot \left(-\dfrac{6}{5}\right) \cdot x^{-\frac{6}{5}-1} \cr \cr &=& -18 \cdot x^{-\frac{11}{5}} \cr \cr &=& -18 \cdot \dfrac{1}{\sqrt[5]{x^{11}}} \cr \cr &=& -\dfrac{18}{\sqrt[5]{x^{11}}} \end{array}$

Vorgehen: Faktor- und Potenzregel
 

20)
$\begin{array}{rcl}\mathbb{D}&=&\mathbb{R} \cr \cr f'(x) &=& 7 \cdot a \cdot x^{a-1}+0 \cr &=& 7ax^{a-1} \end{array}$

Vorgehen: Konstanten-, Faktor-, Summen- und Potenzregel

 
Bemerkung zu den folgenden Aufgaben: Bitte beachten Sie, dass die Anwendung der Konstanten-, Faktor- und Summenregel nicht mehr explizit erwähnt wird, um den Blick auf die weitergehenden Ableitungsregeln zu lenken - auch wenn man die einfachen Ableitungsregeln (fast) bei jeder Aufgabe benötigt. Auch Hinweise zu speziellen Ableitungen wird nicht mehr notiert - dass man z. B. zum Ableiten einer Exponentialfunktion die Regel für die Exponentialfunktion benötigt, ist ja naheliegend ...

3. Aufgabe

Eine Bemerkung vorab: Die Funktionen 1) bis 5) könnte man auch gut ohne die Produktregel ableiten. Um genau zu sein, wäre es meist sogar sinnvoller, die Funktionsterme auszumultiplizieren und dann einfach die Regel für Polynome anzuwenden. In diesen Beispielen wurde nur deswegen die Produktregel angewendet, damit es auch ein paar leichte Beispiele gibt.

1) 
$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\f(x) &=& \left(x-1\right)\cdot\left(\dfrac{47}{2}x^2+16x+7\right)\\\\\quad u(x) &=& x-1 &\Rightarrow & u'(x) &=& 1\\\quad v(x) &=& \dfrac{47}{2}x^2+16x+7 &\Rightarrow & v'(x) &=& 47x+16\\\\f'(x) &=& 1\cdot \left(\dfrac{47}{2}x^2+16x+7\right)+\left(x-1\right)\cdot\left(47x+16\right)\\\\&=& \dfrac{47}{2}x^2+16x+7+47x^2+16x-47x-16\\\\&=& \dfrac{141}{2}x^2-15x-9\end{array}$

2)

$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\f(x) &=& \left(13x^2+\dfrac{7}{5}x-18\right)\left(11x^2-\dfrac{15}{4}x-1\right)\\\\\quad u(x) &=& 13x^2+\dfrac{7}{5}x-18 &\Rightarrow & u'(x) = 26x+\dfrac{7}{5}\\\\\quad v(x) &=& 11x^2-\dfrac{15}{4}x-1 &\Rightarrow & v'(x) = 22x-\dfrac{15}{4}\\\\\\f'(x) &=& \left(26x+\dfrac{7}{5}\right)\cdot\left(11x^2-\dfrac{15}{4}x-1\right)+\left(13x^2+\dfrac{7}{5}x-18\right)\cdot\left(22x-\dfrac{15}{4}\right)\\\\&=& 286x^3-\dfrac{195}{2}x^2-26x+\dfrac{77}{5}x^2-\dfrac{21}{4}x-\dfrac{7}{5}+286x^3-\dfrac{195}{4}x^2+\dfrac{154}{5}x^2-\dfrac{21}{4}x-396x+\dfrac{135}{2}\\\\&=& 572x^3-\dfrac{2.001}{20}x^2-\dfrac{865}{2}x+\dfrac{661}{10}\end{array}$

3)
$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\f(x) &=& \left(\dfrac{1}{8}x^3+5x\right)\cdot\sqrt{8}x\\\\\quad u(x) &=& \dfrac{1}{8}x^3+5x &\Rightarrow & u'(x) &=& \dfrac{3}{8}x^{2}+5\\\quad v(x) &=& \sqrt{8}x &\Rightarrow & v'(x) &=& \sqrt{8}\\\\f'(x) &=& \left(\dfrac{3}{8}x^{2}+5\right)\cdot\sqrt{8}x+\left(\dfrac{1}{8}x^3+5x\right)\cdot\sqrt{8}\\\\&=& \sqrt{8}\left(\dfrac{3}{8}x^{3}+5x+\dfrac{1}{8}x^3+5x\right)\\\\&=& \sqrt{8}\left(\dfrac{1}{2}x^{3}+10x\right)\\\end{array}$

4)
$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\f(x) &=& 3x^2\cdot 7x^{\frac{1}{2}}+ex^{10}-105\\\\\quad u(x) &=& 3x^2 &\Rightarrow & u'(x) &=& 6x\\\quad v(x) &=& 7x^{\frac{1}{2}} &\Rightarrow & v'(x) &=& \dfrac{7}{2}x^{-\frac{1}{2}}\\\\f'(x) &=& 6x\cdot 7x^{\frac{1}{2}}+3x^2\cdot \dfrac{7}{2}x^{-\frac{1}{2}}+10ex^9\\\\&=& 42x^1\cdot x^{\frac{1}{2}}+\dfrac{21}{2}x^2\cdot x^{-\frac{1}{2}}+10ex^9\\\\&=& 42x^{\frac{3}{2}}+\dfrac{21}{2}x^{\frac{3}{2}}+10ex^9\\\\&=& \dfrac{105}{2}x^{\frac{3}{2}}+10ex^9\\\\&=& \dfrac{105}{2}\sqrt{x^3}+10ex^9\\\end{array}$

Bemerkung: $ex^{10}$ muss nicht mit der Produktregel abgeleitet werden. $e$ ist ja einfach nur eine Zahl. Daher greift die Faktorregel.

5)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\g(k) &=& \left(\dfrac{11}{6}k^2-k\right)^2\cdot 72 \\&=& 72\left(\dfrac{11}{6}k^2-k\right)\cdot\left(\dfrac{11}{6}k^2-k\right) \\\\\quad u(k) &=& 72\left(\dfrac{11}{6}k^2-k\right) = 132k^2-72k &\Rightarrow & u'(k)&=& 264k-72 \\\quad v(k) &=& \dfrac{11}{6}k^2-k &\Rightarrow &v'(k) &=& \dfrac{11}{3}k-1 \\\\g'(k) &=& \left(264k-72\right)\cdot\left(\dfrac{11}{6}k^2-k\right)+\left(132k^2-72k\right)\cdot\left(\dfrac{11}{3}k-1\right) \\&=&484k^3-264k^2-132k^2+72k+484k^3-132k^2-264k^2+72k \\&=& 968k^3-792k^2+144k\end{array}$

6)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R}^+_0 \\\\f(x) &=& \left(4x^2-16\right)\sqrt{23x}-5 \\\\\quad u(x) &=& 4x^2-16 &\Rightarrow & u'(x) &=& 8x \\\quad v(x) &=& \sqrt{23x} = \sqrt{23}\sqrt{x} &\Rightarrow & v'(x) &=& \sqrt{23}\dfrac{1}{2\sqrt{x}} = \dfrac{\sqrt{23}}{2\sqrt{x}} \\\\f'(x) &=& 8x\cdot \sqrt{23x}+\left(4x^2-16\right)\cdot \dfrac{\sqrt{23}}{2\sqrt{x}} \\\\&=& 8x\sqrt{23x}+\dfrac{2x^2\sqrt{23}}{\sqrt{x}}-\dfrac{8\sqrt{23}}{\sqrt{x}}\end{array}$

7)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R}^+_0 \\\\g(x) &=& 2^x\sqrt[10]{1024x} \\&=& 2^x\cdot 2\sqrt[10]{x} \\\\\quad u(x) &=& 2^x &\Rightarrow & u'(x)&=& 2^x\cdot\ln(2) \\\quad v(x) &=& 2\sqrt[10]{x} = 2x^{\frac{1}{10}} &\Rightarrow & v'(x) &=& 2\cdot\dfrac{1}{10}x^{-\frac{9}{10}} = \dfrac{1}{5\sqrt[10]{x^9}} \\\\f'(x) &=& 2^x\cdot\ln(2)\cdot 2\sqrt[10]{x}+2^x\cdot \dfrac{1}{5}\cdot\dfrac{1}{\sqrt[10]{x^9}} \\\\&=& 2^{x+1}\cdot\ln(2)\sqrt[10]{x}+2^{x+1}\cdot\dfrac{1}{10\sqrt[10]{x^9}} \\\\&=& 2^{x+1}\left(\dfrac{1}{10\sqrt[10]{x^9}}+\ln(2)\sqrt[10]{x}\right)\end{array}$

8)
$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\f(x) &=& 23x^2\cdot e^x\\\\\quad u(x) &=& 23x^2 &\Rightarrow & u'(x) &=& 46x\\\quad v(x) &=& e^x &\Rightarrow & v'(x) &=& e^x\\\\f'(x) &=& 46x\cdot e^x+23x^2\cdot e^x\\&=& e^x\left(46x+23x^2\right)\\&=& 23xe^x\left(2+x\right)\\\end{array}$

9)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\f(k) &=& \dfrac{5}{4}k^{12}\cdot e^k-1 \\\\\quad u(k) &=& \dfrac{5}{4}k^{12} &\Rightarrow & u'(k) &=& 15k^{11} \\\quad v(k) &=& e^k &\Rightarrow &v'(k) &=& e^k \\\\f'(k) &=& 15k^{11}\cdot e^k+\dfrac{5}{4}k^{12}\cdot e^k \\\\&=& k^{11}e^k\left(15+\dfrac{5}{4}k\right)\end{array}$

10)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R}\setminus_{\{0\}} \\\\f(y) &=& \dfrac{16}{\frac{4}{3}y^7 e^{-y}}-\dfrac{14}{9} \\&=& 12y^{-7}e^y -\dfrac{14}{9} \\\\\quad u(y) &=& 12y^{-7} &\Rightarrow & u'(y)&=& -84y^{-8} \\\quad v(y) &=& e^y &\Rightarrow & v'(y) &=& e^y \\\\f'(y) &=& -84y^{-8}\cdot e^y+12y^{-7}\cdot e^y \\ &=& 12y^{-8}e^y(-7+y) \\&=& \dfrac{12e^y(y-7)}{y^8}\end{array}$

11)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R} \\\\f(x) &=& 5{,}5^x\cdot x^5-5 \\\\\quad u(x) &=& 5{,}5^x &\Rightarrow & u'(x) &=& 5{,}5^x\cdot\ln(5{,}5) \\\quad v(x) &=& x^5 &\Rightarrow & v'(x) &=& 5x^4 \\\\f'(x) &=& 5{,}5^x\cdot\ln(5{,}5)\cdot x^5+5{,}5^x\cdot 5x^4 \\&=& 5{,}5^x x^4\left(x\ln(5{,}5)+5\right)\end{array}$

12)
$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}^+ \\\\f(x) &=& 19x^2\cdot\ln(x)\\\\\quad u(x) &=& 19x^2 &\Rightarrow & u'(x) &=& 38x\\\quad v(x) &=& \ln(x) &\Rightarrow & v'(x) &=& \dfrac{1}{x}\\\\f'(x) &=& 38x\cdot\ln(x)+19x^2\cdot\dfrac{1}{x}\\&=& 38x\cdot\ln(x)+19x\\&=& x\left(38\ln(x)+19\right)\\\end{array}$

13)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R}^+ \\\\f(a) &=& -14\sqrt[4]{a}\cdot \log_4(a) \\\\\quad u(a) &=& -14\sqrt[4]{a} = -14a^{\frac{1}{4}} &\Rightarrow & u'(a) &=& -14\cdot\frac{1}{4}a^{-\frac{3}{4}} = -\dfrac{7}{2}a^{-\frac{3}{4}} \\\quad v(a) &=& \log_4(a) &\Rightarrow & v'(a) &=& \dfrac{1}{a\ln(4)} \\\\f'(a) &=& -\dfrac{7}{2}a^{-\frac{3}{4}}\cdot \log_4(a)-14\sqrt[4]{a}\cdot \dfrac{1}{a\ln(4)} \\&=& -\dfrac{7}{2}a^{-\frac{3}{4}}\cdot\log_4(a)-14a^{-\frac{3}{4}}\cdot\dfrac{1}{\ln(4)} \\&=& -\dfrac{7}{\sqrt[4]{a^3}}\left(\dfrac{\log_4(a)}{2}+\dfrac{2}{\ln(4)}\right)\end{array}$

14)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R}^+ \\\\f(x) &=& \dfrac{15}{x^2}\ln(x)+125 \\\\\quad u(x) &=& \dfrac{15}{x^2} = 15x^{-2} &\Rightarrow &u'(x) &=& 15\cdot(-2)x^{-3} = -\dfrac{30}{x^3} \\\quad v(x) &=& \ln(x) &\Rightarrow &v'(x) &=& \dfrac{1}{x} \\\\f'(x) &=& -\dfrac{30}{x^3}\ln(x)+\dfrac{15}{x^2}\cdot \dfrac{1}{x} \\\\&=& \dfrac{15-30\ln(x)}{x^3}\end{array}$

15)
$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\f(x) &=& 2x\cdot 3\sin(x)\\&=& 6x\cdot\sin(x)\\\\\quad u(x) &=& 6x &\Rightarrow & u'(x) &=& 6\\\quad v(x) &=& \sin(x) &\Rightarrow & v'(x) &=& \cos(x)\\\\f'(x) &=& 6\cdot\sin(x)+6x\cdot\cos(x)\\&=& 6\left(sin(x)+x\cos(x)\right)\\\end{array}$

16)
$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\f(x) &=& \sin(x)\cdot\cos(x)-\dfrac{3}{\pi}\\\\\quad u(x) &=& \sin(x) &\Rightarrow & u'(x) &=& \cos(x)\\\quad v(x) &=& \cos(x) &\Rightarrow & v'(x) &=& -\sin(x)\\\\f'(x) &=& \cos(x)\cdot\cos(x)+\sin(x)\cdot \left(-\sin(x)\right)-0\\&=& \cos^2(x)-\sin^2(x)\\\end{array}$

17)
$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}\\\quad a &\in& \mathbb{R}\\\\f(x) &=& ax^2\cdot 5^3\sin(x)+17ax^3\\&=& 125ax^2\cdot\sin(x)+17ax^3\\\\\quad u(x) &=& 125ax^2 &\Rightarrow & u'(x) &=& 250ax\\\quad v(x) &=& \sin(x) &\Rightarrow & v'(x) &=& \cos(x)\\\\f'(x) &=& 250ax\cdot \sin(x)+125ax^2\cdot\cos(x)+51ax^2\\&=& ax\left(250\sin(x)+125x\cdot\cos(x)+51x\right)\\\end{array}$

18)
$\begin{array}{ccllrcl}\quad\mathbb{D} &=& \mathbb{R}\\\\f(x) &=& e^x\cdot\sin(x)\\\\\quad u(x) &=& e^x &\Rightarrow & u'(x) &=& e^x\\\quad v(x) &=& \sin(x) &\Rightarrow & v'(x) &=& \cos(x)\\\\f'(x) &=& e^x\cdot\sin(x)+e^x\cdot\cos(x)\\&=& e^x\left(\sin(x)+\cos(x)\right)\\\end{array}$

19)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R}\setminus_{\{k\pi+\frac{\pi}{2}; k \in \mathbb{Z}\}} \\\\f(x) &=& -6x^3\tan(x)-18 \\\\\quad u(x) &=& -6x^3 &\Rightarrow &u'(x)&=& -18x^2 \\\quad v(x) &=& \tan(x) &\Rightarrow &v'(x) &=& \dfrac{1}{\cos^2(x)} \\\\f'(x) &=& -18x^2\cdot\tan(x)-6x^3\cdot \dfrac{1}{\cos^2(x)} \\&=& -6x^2\left(3\tan(x)+\dfrac{x}{\cos^2(x)}\right)\end{array}$

20)
$\begin{array}{cclcrcl}\quad\mathbb{D} &=& \mathbb{R}\setminus_{\{k\pi+\frac{\pi}{2}; k \in \mathbb{Z}\}} \\\\f(s) &=& -\tan(s)\left(\dfrac{s}{\pi}+\cos(s)\right) \\\\\quad u(s) &=& -\tan(s) &\Rightarrow & u'(s)&=& -\dfrac{1}{\cos^2(s)} \\\quad v(s) &=& \dfrac{1}{\pi}s+\cos(s) &\Rightarrow & v'(s) &=& \dfrac{1}{\pi}-\sin(s) \\\\f'(s) &=& -\dfrac{1}{\cos^2(s)}\cdot \left(\dfrac{s}{\pi}+\cos(s)\right) -\tan(s)\cdot \left(\dfrac{1}{\pi}-\sin(s)\right)\end{array}$

4. Aufgabe

1)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{100\right\}} \cr \cr f(x) &=& \dfrac{x^{4}}{100 - x} \cr \cr \quad u(x) &=& x^{4} & \Rightarrow & u'(x) &=&4 x^{3}\cr \quad v(x) &=&100 - x & \Rightarrow & v'(x) &=& -1\cr \cr f'(x) &=& \dfrac{4 x^{3}\cdot \left(100 - x\right)-x^{4} \cdot \left(-1\right)}{\left(100 - x\right)^2} \cr \cr &=& \dfrac{400x^3-4x^4+x^{4}}{\left(100 - x\right)^{2}}\cr \cr &=& \dfrac{x^{3} \left(400 - 3 x\right)}{\left(100 - x\right)^{2}}\end{array}$

2)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{0\right\}}\cr \cr f(x) &=& \dfrac{\dfrac{x^{2}}{9} + 1}{- 27 x^{13}} \cr \cr \quad u(x) &=& \dfrac{x^{2}}{9} + 1 & \Rightarrow & u'(x) &=&\dfrac{2}{9}x \cr \quad v(x) &=&- 27 x^{13} & \Rightarrow & v'(x) &=& - 351 x^{12}\cr \cr f'(x) &=& \dfrac{\dfrac{2}{9}x\cdot \left(- 27 x^{13}\right)-\left(\dfrac{x^{2}}{9} + 1 \right)\cdot \left(- 351 x^{12}\right)}{\left(- 27 x^{13}\right)^2}\cr \cr &=& \dfrac{- 6 x^{14}+ 39 x^{14} + 351x^{12}}{729 x^{26}}\cr \cr &=& \dfrac{x^{12} \left(33 x^{2} + 351\right)}{729 x^{26}}\cr \cr &=& \dfrac{11 x^{2} + 117}{243 x^{14}}\end{array}$

3)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{\frac{7}{12}\right\}} \cr \cr f(q) &=& \dfrac{\left(- 12 q+7\right)^{4}}{144 q^{2} - 168 q + 49}\cr \cr &=& \dfrac{\left(- 12 q+7\right)^{4}}{\left(- 12 q+7\right)^{2}} \cr \cr &=& \left( - 12 q+7\right)^{2}\cr \cr &=& 144q^2-168q + 49\cr \cr \cr f'(q) &=& 288 q - 168\end{array}$

Bemerkung: Diese Funktion kann man so umformen, dass sie ohne die Quotientenregel abgeleitet werden kann. Das ist natürlich viel einfacher.

4)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{-5\right\}}\cr \cr f(x) &=& \dfrac{x^{3}}{x + 5}\cr \cr \quad u(x) &=& x^{3} & \Rightarrow & u'(x) &=&3 x^{2}\cr \quad v(x) &=&x + 5 & \Rightarrow & v'(x) &=& 1 \cr \cr f'(x) &=& \dfrac{3 x^{2}\cdot \left(x + 5\right)-x^{3} \cdot 1}{\left(x + 5\right)^2}\cr \cr &=& \dfrac{3x^{3} + 15x^2-x^{3}}{\left(x + 5\right)^{2}}\cr \cr &=& \dfrac{x^{2} \left(2 x + 15\right)}{\left(x + 5\right)^{2}}\end{array}$

5)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{0\right\}}\cr \cr f(x) &=& \dfrac{4 x + 2}{7 x^{2}}\cr \cr \quad u(x) &=& 4 x + 2 & \Rightarrow & u'(x) &=&4\cr \quad v(x) &=&7 x^{2} & \Rightarrow & v'(x) &=& 14 x\cr \cr f'(x) &=& \dfrac{4 \cdot 7 x^{2}-\left(4 x + 2 \right)\cdot 14 x}{\left(7 x^{2}\right)^2}\cr \cr &=& \dfrac{28 x^{2}-56 x^{2}-28x}{49 x^{4}}\cr \cr &=& \dfrac{- 28 x \left(x + 1\right)}{49 x^{4}}\cr \cr &=& - \dfrac{4 x + 4}{7 x^{3}}\end{array}$

6)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{- \frac{2}{9}\right\}}\cr \cr f(x) &=& \dfrac{3 x + 5}{9 x + 2}\cr \cr \quad u(x) &=& 3 x + 5 & \Rightarrow & u'(x) &=&3\cr \quad v(x) &=&9 x + 2 & \Rightarrow & v'(x) &=& 9\cr \cr f'(x) &=& \dfrac{3 \cdot \left(9 x + 2\right)-\left(3 x + 5 \right)\cdot 9}{\left(9 x + 2\right)^2}\cr \cr &=& \dfrac{27 x + 6-27 x - 45}{\left(9 x + 2\right)^{2}}\cr \cr &=& \dfrac{-39}{\left(9 x + 2\right)^{2}}\end{array}$

7)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\cr \cr f(z) &=& \dfrac{23}{z^{-42}}\cr \cr &=& 23z^{42}\cr \cr\cr f'(z) &=& 42 \cdot 23z^{41}\cr \cr &=& 966z^{41}\end{array}$

Bemerkung: Auch diese Funktion kann man so umformen, dass sie ohne die Quotientenregel abgeleitet werden kann.

8)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x) &=& \dfrac{x}{2 x^{2} + 4} \cr \cr \quad u(x) &=& x & \Rightarrow & u'(x) &=&1\cr \quad v(x) &=&2 x^{2} + 4 & \Rightarrow & v'(x) &=& 4 x \cr \cr f'(x) &=& \dfrac{1 \cdot \left(2 x^{2} + 4\right)-x \cdot 4 x}{\left(2 x^{2} + 4\right)^2} \cr \cr &=& \dfrac{2 x^{2} + 4-4 x^{2}}{\left(2x^{2} + 4\right)^{2}} \cr \cr &=& \dfrac{4 - 2 x^{2}}{4\left(x^{2} + 2\right)^{2}} \cr \cr &=& \dfrac{2 - x^{2}}{2 \left(x^{2} + 2\right)^{2}} \end{array}$

9)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{\sqrt[3]{-32}\right\}}\cr \cr f(x) &=& \dfrac{15 x^{2} - 8 x}{x^{3} + 32}\cr \cr \quad u(x) &=& 15 x^{2} - 8 x & \Rightarrow & u'(x) &=&30 x - 8\cr \quad v(x) &=&x^{3} + 32 & \Rightarrow & v'(x) &=& 3 x^{2}\cr \cr f'(x) &=& \dfrac{\left(30 x - 8\right )\cdot \left(x^{3} + 32\right)-\left(15 x^{2} - 8 x \right)\cdot 3 x^{2}}{\left(x^{3} + 32\right)^2}\cr \cr &=& \dfrac{30x^4-8x^3+960x-256-45x^4+24x^3}{\left(x^{3} + 32\right)^{2}}\cr \cr &=& \dfrac{- 15 x^{4} + 16 x^{3} + 960 x - 256}{\left(x^{3} + 32\right)^{2}}\end{array}$

10)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{\frac{3}{2}\right\}}\cr \cr f(x) &=& \dfrac{8 x + 3}{4 x - 6} \cr \cr \quad u(x) &=& 8 x + 3 & \Rightarrow & u'(x) &=&8\cr \quad v(x) &=&4 x - 6 & \Rightarrow & v'(x) &=& 4\cr \cr f'(x) &=& \dfrac{8\cdot \left(4 x - 6\right)-\left(8 x + 3 \right)\cdot 4}{\left(4 x - 6\right)^2} \cr \cr &=& \dfrac{32 x - 48-32 x - 12}{\left(4 x - 6\right)^{2}}\cr \cr &=& \dfrac{-60}{4\left(2x - 3\right)^{2}} \cr \cr &=& - \dfrac{15}{\left(2 x - 3\right)^{2}}\end{array}$

11)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}^+\cr \cr f(w) &=& \dfrac{w - 13}{- 8 \sqrt{w}}\cr \cr \quad u(w) &=& w - 13 & \Rightarrow & u'(w) &=&1\cr \quad v(w) &=&- 8 \sqrt{w} = -8w^{\frac{1}{2}} & \Rightarrow & v'(w) &=& -8\cdot\dfrac{1}{2}w^{-\frac{1}{2}} = - \dfrac{4}{\sqrt{w}} \cr \cr f'(w) &=& \dfrac{1\cdot \left(- 8 \sqrt{w}\right)-\left(w - 13 \right)\cdot \left(- \dfrac{4}{\sqrt{w}}\right)}{\left(- 8 \sqrt{w}\right)^2} \cr \cr &=& \dfrac{-\dfrac{8w}{\sqrt{w}}+\dfrac{4w - 52}{\sqrt{w}}}{64 w} \cr \cr &=& \dfrac{\dfrac{-4 w - 52}{\sqrt{w}}}{64 w} \cr \cr &=& -\dfrac{4(w +13)}{\sqrt{w}}\cdot\dfrac{1}{64 w} \cr \cr &=& - \dfrac{w + 13}{16 \sqrt{w^3}}\end{array}$

12)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{10\right\}} \cr \cr f(x) &=& \dfrac{12 \sqrt{x}}{x - 10} \cr \cr \quad u(x) &=& 12 \sqrt{x} = 12x^{\frac{1}{2}} & \Rightarrow & u'(x) &=& 12\cdot\dfrac{1}{2}x^{-\frac{1}{2}} = \dfrac{6}{\sqrt{x}}\cr \quad v(x) &=&x - 10 & \Rightarrow & v'(x) &=& 1\cr \cr f'(x) &=& \dfrac{\dfrac{6}{\sqrt{x}}\cdot \left(x - 10\right)-12 \sqrt{x}\cdot 1}{\left(x - 10\right)^2} \cr \cr &=& \dfrac{\dfrac{6x - 60}{\sqrt{x}}-\dfrac{12x}{\sqrt{x}}}{\left(x - 10\right)^{2}} \cr \cr &=& \dfrac{\dfrac{-6 x - 60}{\sqrt{x}}}{\left(x - 10\right)^{2}} \cr \cr &=& -\dfrac{6 x + 60}{\sqrt{x}}\cdot\dfrac{1}{\left(x - 10\right)^{2}} \cr \cr &=& - \dfrac{6 x + 60}{\sqrt{x} \left(x - 10\right)^{2}} \end{array}$

13)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\cr \cr f(z) &=& \dfrac{2^{z} - 1}{4^{z}} \cr \cr \quad u(z) &=& 2^{z} - 1 & \Rightarrow & u'(z) &=&2^{z} \ln{\left(2 \right)}\cr \quad v(z) &=&4^{z} & \Rightarrow & v'(z) &=& 4^{z} \ln{\left(4 \right)}\cr \cr f'(z) &=& \dfrac{2^{z} \ln\left(2 \right)\cdot4^z-\left(2^{z} - 1 \right)\cdot 4^{z} \ln{\left(4 \right)}}{\left(4^{z}\right)^2}\cr \cr &=& \dfrac{8^{z} \ln{\left(2 \right)}-4^{z} \cdot 2^{z} \ln{\left(4 \right)}+4^z\ln{\left(4\right)}}{4^{2 z}} \cr \cr &=& \dfrac{8^{z} \ln{\left(2 \right)}-8^{z} \ln{\left(2^2 \right)}+4^z\ln{\left(2^2\right)}}{4^{2 z}} \cr\cr &=& \dfrac{8^{z} \ln{\left(2 \right)}-8^{z} \cdot 2\ln{\left(2 \right)}+4^z\cdot 2\ln{\left(2\right)}}{4^{2 z}} \cr \cr &=& \dfrac{\left(2 \cdot 4^{z} - 8^{z}\right) \ln{\left(2 \right)}}{16^z} \cr \cr &=& 16^{- z} \left(2 \cdot 4^{z} - 8^{z}\right) \ln{\left(2 \right)}\end{array}$

14)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{- \frac{1}{7}\right\}}\cr \cr f(x) &=& \dfrac{21 e^{x}}{7 x + 1}\cr \cr \quad u(x) &=& 21 e^{x} & \Rightarrow & u'(x) &=&21 e^{x}\cr \quad v(x) &=&7 x + 1 & \Rightarrow & v'(x) &=& 7\cr \cr f'(x) &=& \dfrac{21 e^{x}\cdot \left(7 x + 1\right)-21 e^{x}\cdot 7}{\left(7 x + 1\right)^2}\cr \cr &=& \dfrac{147x e^x + 21 e^{x}-147 e^{x}}{\left(7 x + 1\right)^{2}}\cr \cr &=& \dfrac{\left(147 x - 126\right) e^{x}}{\left(7 x + 1\right)^{2}}\end{array}$

15)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{0\right\}} \cr \cr f(x) &=& \dfrac{17 e^{x} - 1}{34 x^{2}} \cr \cr \quad u(x) &=& 17 e^{x} - 1 & \Rightarrow & u'(x) &=&17 e^{x}\cr \quad v(x) &=&34 x^{2} & \Rightarrow & v'(x) &=& 68 x \cr \cr f'(x) &=& \dfrac{17 e^{x}\cdot 34 x^{2}-\left(17 e^{x} - 1 \right)\cdot 68 x}{\left(34 x^{2}\right)^2} \cr \cr &=& \dfrac{578 x^{2} e^{x}-1.156x e^{x} +68x}{1.156 x^{4}}\cr \cr &=& \dfrac{34 x \left(17 x e^{x} - 34 e^{x} + 2\right)}{1.156 x^{4}} \cr \cr &=& \dfrac{17 x e^{x} - 34 e^{x} + 2}{34 x^{3}} \end{array}$

16)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}^+\setminus_{\left\{1\right\}} \cr \cr f(x) &=& \dfrac{x^{2} + 18}{18 \lg\left(x \right)} \cr \cr \quad u(x) &=& x^{2} + 18 & \Rightarrow & u'(x) &=&2 x\cr \quad v(x) &=&18 \lg\left(x \right) & \Rightarrow & v'(x) &=& \dfrac{18}{x \ln{\left(10 \right)}}\cr \cr f'(x) &=& \dfrac{2 x\cdot 18 \lg\left(x \right)-\left(x^{2} + 18 \right)\cdot \dfrac{18}{x \ln{\left(10 \right)}}}{\left(18 \lg\left(x \right)\right)^2} \cr \cr &=& \dfrac{36 x \lg{\left(x \right)}-\dfrac{18x^{2} + 324}{x \ln{\left(10 \right)}}}{324 \lg^2{\left(x \right)}} \cr\cr &=& \dfrac{\dfrac{36 x^2 \ln(10)\lg{\left(x \right)}}{x \ln(10)}-\dfrac{18x^{2} + 324}{x \ln{\left(10 \right)}}}{324 \lg^2{\left(x \right)}} \cr\cr &=& \dfrac{18 \left(2 x^{2} \ln(10)\lg{\left(x \right)} - x^{2} - 18\right)}{x \ln{\left(10 \right)}}\cdot\dfrac{1}{324 \lg^2{\left(x \right)}} \cr \cr &=& \dfrac{2 x^{2} \ln(10)\lg{\left(x \right)} - x^{2} - 18}{18 x \ln(10) \lg^2{\left(x \right)}}\end{array}$

17)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{0\right\}}\cr \cr f(x) &=& \dfrac{\ln{\left(x \right)}}{x^{11}} \cr \cr \quad u(x) &=& \ln{\left(x \right)} & \Rightarrow & u'(x) &=&\dfrac{1}{x}\cr \quad v(x) &=&x^{11} & \Rightarrow & v'(x) &=& 11 x^{10}\cr \cr f'(x) &=& \dfrac{\dfrac{1}{x}\cdot x^{11}-\ln{\left(x \right)} \cdot 11 x^{10}}{\left(x^{11}\right)^2}\cr \cr &=& \dfrac{x^{10}-11 x^{10} \ln{\left(x \right)}}{x^{22}}\cr \cr &=& \dfrac{x^{10} \left(1 - 11 \ln{\left(x \right)}\right)}{x^{22}} \cr \cr &=& \dfrac{1 - 11 \ln{\left(x \right)}}{x^{12}}\end{array}$

18)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{0; 1\right\}} \cr \cr g(x) &=& \dfrac{- 2 \ln{\left(x \right)}}{x^{31} - x^{26}} \cr \cr \quad u(x) &=& - 2 \ln{\left(x \right)} & \Rightarrow & u'(x) &=&- \dfrac{2}{x}\cr \quad v(x) &=&x^{31} - x^{26} & \Rightarrow & v'(x) &=& 31 x^{30} - 26 x^{25} \cr \cr g'(x) &=& \dfrac{- \dfrac{2}{x}\cdot \left(x^{31} - x^{26}\right)-\left(- 2 \ln{\left(x \right)} \right)\cdot \left(31 x^{30} - 26 x^{25}\right)}{\left(x^{31} - x^{26}\right)^2} \cr \cr &=& \dfrac{-2 x^{30} +2x^{25} +62 x^{30}\ln{\left(x \right)}-52x^{25}\ln\left(x\right)}{\left(x^{31} - x^{26}\right)^{2}} \cr\cr &=& \dfrac{2 x^{25} \left(- x^{5} + 1 + 31 x^{5} \ln\left(x\right) - 26 \ln{\left(x \right)}\right)}{x^{52}\left(x^{5} - 1\right)^{2}} \cr\cr &=& \dfrac{2 \left(- x^{5} + \left(31 x^{5} - 26\right) \ln{\left(x \right)} + 1\right)}{x^{27}\left(x^{5} - 1\right)^{2}}\end{array}$

19)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\left\{0\right\}}\cr \cr f(y) &=& \dfrac{\pi \sin{\left(y \right)}}{- y^{2}} -12\pi\cr \cr \quad u(y) &=& \pi \sin{\left(y \right)} & \Rightarrow & u'(y) &=&\pi \cos{\left(y \right)}\cr \quad v(y) &=&- y^{2} & \Rightarrow & v'(y) &=& - 2 y\cr \cr f'(y) &=& \dfrac{\pi \cos{\left(y \right)}\cdot \left(- y^{2}\right)-\pi \sin{\left(y \right)} \cdot \left(- 2 y\right)}{\left(- y^{2}\right)^2}\cr \cr &=& \dfrac{- \pi y^{2} \cos{\left(y \right)}+2 \pi y \sin{\left(y \right)}}{y^{4}}\cr \cr &=& \dfrac{\pi y \left(- y \cos{\left(y \right)} + 2 \sin{\left(y \right)}\right)}{y^{4}}\cr \cr &=& \dfrac{\pi \left(- y \cos{\left(y \right)} + 2 \sin{\left(y \right)}\right)}{y^{3}}\end{array}$   

 
20)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\left\{t \in \mathbb{R}\; |\; t\neq \frac{\pi}{2}+2 k \pi \text{ und } t\neq \frac{3\pi}{2}+2 k \pi , k \in \mathbb{Z} \right\} \cr \cr y(t) &=& \dfrac{\sin{\left(t \right)}}{\cos{\left(t \right)}} \cr \cr \quad u(t) &=& \sin{\left(t \right)} & \Rightarrow & u'(t) &=&\cos{\left(t \right)}\cr \quad v(t) &=&\cos{\left(t \right)} & \Rightarrow & v'(t) &=& - \sin{\left(t \right)} \cr \cr y'(t) &=& \dfrac{\cos{\left(t \right)}\cdot \cos{\left(t \right)}-\sin{\left(t \right)}\cdot \left(- \sin{\left(t \right)}\right)}{\left(\cos{\left(t \right)}\right)^2} \cr \cr &=& \dfrac{\cos^{2}{\left(t \right)}+ \sin^{2}{\left(t \right)}}{\cos^{2}{\left(t \right)}} \cr \cr &=& \dfrac{1}{\cos^{2}{\left(t \right)}} \end{array}$

5. Aufgabe

1)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R} \cr \cr f(x) &=& (2x+1)^7 \cr \cr \quad g(h(x)) &=& (h(x))^7 &\Rightarrow& g'(h(x)) &=& 7(h(x))^6 \cr \quad h(x) &=& 2x+1 &\Rightarrow& h'(x) &=& 2 \cr \cr f'(x) &=& 7(2x+1)^6\cdot 2 \cr &=& 14(2x+1)^6\end{array}$

2)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R}\setminus_{\{0\}} \\\\f(x) &=& 24\left(x+\dfrac{7}{8x}\right)^2 \\\\\quad g(h(x)) &=& 24\left(h(x)\right)^2 & \Rightarrow & g'(h(x)) &=& 48h(x) \\\quad h(x) &=& x+\dfrac{7}{8x} = x+\dfrac{7}{8}x^{-1} & \Rightarrow & h'(x) &=& 1-\dfrac{7}{8}x^{-2} = 1-\dfrac{7}{8x^2} \\\\f'(x) &=& 48\left(x+\dfrac{7}{8x}\right)\cdot \left(1-\dfrac{7}{8x^2}\right) \\\\&=& 48\left(x-\dfrac{7}{8x}+\dfrac{7}{8x}-\dfrac{49}{64x^3}\right) \\\\&=& 48\left(x-\dfrac{49}{64x^3}\right) \\\\&=& 48x-\dfrac{147}{4x^3}\end{array}$

3)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R}\setminus_{\{0; 1\}} \\\\f(x) &=& \dfrac{-63}{x^2-\frac{1}{x}} \\&=& -63\left(x^2-\dfrac{1}{x}\right)^{-1} \\\\\quad g(h(x)) &=& -63\left(h(x)\right)^{-1} & \Rightarrow & g'(h(x)) &=& 63\left(h(x)\right)^{-2} \\\quad h(x) &=& x^2-\dfrac{1}{x} = x^2-x^{-1} & \Rightarrow & h'(x) &=& 2x+x^{-2} = 2x+\dfrac{1}{x^2} \\\\f'(x) &=& 63\left(x^2-\dfrac{1}{x}\right)^{-2}\cdot\left(2x+\dfrac{1}{x^2}\right) \\\\&=& \dfrac{63\cdot\left(2x+\frac{1}{x^2}\right)}{\left(x^2-\frac{1}{x}\right)^{2}} \\\\&=& \dfrac{126x+\frac{63}{x^2}}{\left(x^2-\frac{1}{x}\right)^2}\end{array}$

4)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R}^+ \\\\g(x) &=& \sqrt{112x^3+97x}+16 \\&=& \left(112x^3+97x\right)^{\frac{1}{2}}+16 \\\\\quad g(h(x)) &=& (h(x))^{\frac{1}{2}}+16 & \Rightarrow & g'(h(x)) &=& \dfrac{1}{2}(h(x))^{-\frac{1}{2}} \\\quad h(x) &=& 112x^3+97x & \Rightarrow & h'(x) &=& 336x^2+97 \\\\g'(x) &=& \dfrac{1}{2}\left(112x^3+97x\right)^{-\frac{1}{2}}\cdot \left(336x^2+97\right) \\\\&=& \dfrac{1}{2\left(112x^3+97x\right)^{\frac{1}{2}}}\cdot \left(336x^2+97\right) \\\\&=& \dfrac{336x^2+97}{2\sqrt{112x^3+97x}}\end{array}$

5)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \left]2; \infty\right[ \\\\f(x) &=& \dfrac{1}{\sqrt{3x-6}} \\&=& (3x-6)^{-\frac{1}{2}} \\\\\quad g(h(x)) &=& (h(x))^{-\frac{1}{2}} & \Rightarrow & g'(h(x)) &=& -\dfrac{1}{2}(h(x))^{-\frac{3}{2}} \\\quad h(x) &=& 3x-6 & \Rightarrow & h'(x) &=& 3 \\\\f'(x) &=& -\dfrac{1}{2}(3x-6)^{-\frac{3}{2}}\cdot 3 \\\\&=& -\dfrac{3}{2\cdot (3x-6)^{\frac{3}{2}}} \\\\&=& -\dfrac{3}{2\sqrt{(3x-6)^3}}\end{array}$

6)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \left[-4; \infty\right[ \\\\f(x) &=& \sqrt{(x+4)^3} \\&=& (x+4)^{\frac{3}{2}} \\\\\quad g(h(x)) &=& (h(x))^{\frac{3}{2}} & \Rightarrow & g'(h(x)) &=& \dfrac{3}{2}(h(x))^{\frac{1}{2}} \\ \quad h(x) &=& x+4 & \Rightarrow & h'(x) &=& 1 \\\\f'(x) &=& \dfrac{3}{2}(x+4)^{\frac{1}{2}}\cdot 1 \\\\&=& \dfrac{3}{2}\sqrt{x+4}\end{array}$

7)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R} \\\\f(x) &=& \sqrt[3]{x+4} \\&=& (x+4)^{\frac{1}{3}} \\\\\quad g(h(x)) &=& (h(x))^{\frac{1}{3}} & \Rightarrow & g'(h(x)) &=& \dfrac{1}{3}(h(x))^{-\frac{2}{3}} \\\quad h(x) &=& x+4 & \Rightarrow & h'(x) &=& 1 \\\\f'(x) &=& \dfrac{1}{3}(x+4)^{-\frac{2}{3}}\cdot 1 \\\\&=& \dfrac{1}{3(x+4)^{\frac{2}{3}}} \\\\&=& \dfrac{1}{3\sqrt[3]{(x+4)^2}}\end{array}$

8)
$\begin{array}{lclcrcl} \quad\mathbb{D} &=& \mathbb{R} \\\\f(t) &=& \ln\left(\dfrac{5}{2}t^2+14\right) \\ \\\quad g(h(t)) &=& \ln\left(h(t)\right) & \Rightarrow & g'(h(t)) &=& \dfrac{1}{h(t)} \\\quad h(t) &=& \frac{5}{2}t^2+14 & \Rightarrow & h'(t) &=& 5t \\\\f'(t) &=& \dfrac{1}{\frac{5}{2}t^2+14}\cdot 5t \\&=& \dfrac{5t}{\frac{5}{2}t^2+14}\end{array}$

9)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R}^+ \\\\f(x) &=& \ln\left(\dfrac{12}{7}\cdot \dfrac{1}{\sqrt{x}}\right) \\\\&=& \ln\left(\dfrac{12}{7}x^{-\frac{1}{2}}\right) \\\\\quad g(h(x)) &=& \ln\left(h(x)\right) & \Rightarrow & g'(h(x)) &=& \dfrac{1}{h(x)} \\\\\quad h(x) &=& \dfrac{12}{7}x^{-\frac{1}{2}} & \Rightarrow & h'(x) &=& \dfrac{12}{7}\cdot \left(-\dfrac{1}{2}\right)x^{-\frac{3}{2}} = -\dfrac{6}{7}\cdot x^{-\frac{3}{2}} \\\\f'(x) &=& \dfrac{1}{\dfrac{12}{7}x^{-\frac{1}{2}}} \cdot \left(-\dfrac{6}{7}x^{-\frac{3}{2}}\right) \\\\&=& \dfrac{7}{12}x^{\frac{1}{2}} \cdot \left(-\dfrac{6}{7}\right) x^{-\frac{3}{2}} \\\\&=& -\dfrac{1}{2}x^{-1} \\\\&=& -\dfrac{1}{2x}\end{array}$

10)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \left]-\frac{1}{756};0\right[ \\\\f(x) &=& \ln\left(-42x^4-\dfrac{1}{18}x^3\right) \\\\\quad g(h(x)) &=& \ln\left(h(x)\right) & \Rightarrow & g'(h(x)) &=& \dfrac{1}{h(x)} \\\quad h(x) &=& -42x^4-\dfrac{1}{18}x^3 & \Rightarrow & h'(x) &=& -168x^3-\dfrac{1}{6}x^2 \\\\f'(x) &=& \dfrac{1}{-42x^4-\frac{1}{18}x^3}\cdot \left(-168x^3-\dfrac{1}{6}x^2\right) \\\\&=& \dfrac{-168x^3-\frac{1}{6}x^2}{-42x^4-\frac{1}{18}x^3} \\\\&=& \dfrac{x^2\left(-168x-\frac{1}{6}\right)}{x^2\left(-42x^2-\frac{1}{18}x\right)} \\\\&=& \dfrac{-168x-\frac{1}{6}}{-42x^2-\frac{1}{18}x}\end{array}$

11)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R} \\\\f(x) &=& \left(\sin(x)\right)^2 \\\\\quad g(h(x)) &=& \left(h(x)\right)^2 & \Rightarrow & g'(h(x)) &=& 2h(x) \\\quad h(x) &=& \sin(x) & \Rightarrow & h'(x) &=& \cos(x) \\\\f'(x) &=& 2\sin(x)\cdot \cos(x)\end{array}$

12)
$\begin{array}{lclcrcl}\mathbb{D} &=& \mathbb{R} \\\\g(y) &=& \sqrt{\dfrac{121}{(72a-1)^2+5}} \\\\g'(y) &=& 0 \end{array}$

Bemerkung 1: Da die Funktion $g(y)$ heißt, wissen wir, dass die Variable $y$ ist und nicht $a$, wie man denken könnte. $a$ ist eine Konstante. Damit ist der Funktionsterm konstant und die Ableitung einer Konstanten ist $0$.

Bemerkung 2: Da $(72a-1)^2+5$ immer größer als $0$ ist, darf $a\in\mathbb{R}$ sein.

13)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R}_0^+ \\\\f(x) &=& e^{x^2+\sqrt{x}} \\\\\quad g(h(x)) &=& e^{h(x)} & \Rightarrow & g'(h(x)) &=& e^{h(x)} \\\quad h(x) &=& x^2+\sqrt{x} = x^2+x^{\frac{1}{2}} & \Rightarrow & h'(x) &=& 2x+\dfrac{1}{2}x^{-\frac{1}{2}} = 2x+\dfrac{1}{2\sqrt{x}} \\f'(x) &=& e^{x^2+\sqrt{x}}\cdot\left(2x+\dfrac{1}{2\sqrt{x}}\right) \\\\&=&e^{x^2+\sqrt{x}}\cdot\left(2x+\dfrac{\sqrt{x}}{2x}\right)\end{array}$

14)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R} \\\\f(x) &=& -36\sin\left(\cos(x)\right) \\\\\quad g(h(x)) &=& -36\sin\left(h(x)\right) & \Rightarrow & g'(h(x)) &=& -36\cos\left(h(x)\right) \\ \quad h(x) &=& \cos(x) & \Rightarrow & h'(x) &=& -\sin(x) \\\\ f'(x) &=& -36\cos\left(\cos(x)\right)\cdot \left(-\sin(x)\right) \\&=& 36\cos\left(\cos(x)\right)\cdot\sin(x)\\\end{array}$

Bemerkung: Bei dreifach verketteten Funktionen wie den folgenden Aufgaben 15) bis 18) gibt es beim Ableiten verschiedene Wege: Statt des hier gezeigten Weges können Sie solche Funktionen auch in zwei Schritten ableiten. Am Beispiel von 15) bedeutet das: Sie leiten erst $h(x)=\sin\left(-x^2+13\right)$ ab (mit der Kettenregel natürlich). Dann benötigen Sie zum anschließenden Ableiten von $f(x)$ nur noch einmal die Kettenregel, weil Sie die innere Ableitung bereits vorher berechnet haben. Das Ergebnis ist natürlich in beiden Fällen das gleiche. Insofern können Sie sich einfach aussuchen, welcher Weg für Sie übersichtlicher ist.

15)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R} \\\\f(x) &=& e^{\sin\left(-x^2+13\right)} \\\\\quad g(h(k(x))) &=& e^{h(k(x))} & \Rightarrow & g'(h(k(x))) &=& e^{h(k(x))} \\\quad h(k(x)) &=& \sin(k(x)) & \Rightarrow & h'(k(x)) &=& \cos(k(x)) \\\quad k(x) &=& -x^2+13 & \Rightarrow & k'(x) &=& -2x \\\\f'(x) &=& e^{\sin\left(-x^2+13\right)}\cdot \cos\left(-x^2+13\right) \cdot (-2x) \\&=& -2x\cos\left(-x^2+13\right)\cdot e^{\sin\left(-x^2+13\right)}\end{array}$

16)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R} \\\\f(x) &=& 85\ln\left(e^{3x}+x^2\right)-94 \\\\\quad g(h(k(x))) &=& 85\ln(h(k(x)))-94 & \Rightarrow & g'(h(k(x))) &=& 85\cdot \dfrac{1}{h(k(x))} \\\quad h(k(x)) &=& e^{k(x)}+x^2 & \Rightarrow & h'(k(x)) &=& e^{k(x)}+2x \\\quad k(x) &=& 3x & \Rightarrow & r'(x) &=& 3 \\\\f'(x) &=& 85\cdot \dfrac{1}{e^{3x}+x^2}\cdot \left(e^{3x}\cdot 3+2x\right) \\\\&=& \dfrac{85\cdot \left(3e^{3x}+2x\right)}{e^{3x}+x^2} \\\\&=& \dfrac{\left(255e^{3x}+170x\right)}{e^{3x}+x^2}\end{array}$

17)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R} \\\\f(z) &=& -\dfrac{3}{10}\sqrt{1+\cos\left(z^2\right)} \\\\&=& -\dfrac{3}{10}\left(1+\cos\left(z^2\right)\right)^{\frac{1}{2}} \\\\\quad g(h(k(z))) &=& -\dfrac{3}{10}\left(h(k(z))\right)^{\frac{1}{2}} & \Rightarrow & g'(h(k(z))) &=& -\dfrac{3}{20}\left(h(k(z))\right)^{-\frac{1}{2}} \\\\\quad h(k(z)) &=& 1+\cos\left(k(z)\right) & \Rightarrow & h'(k(z)) &=& -\sin\left(k(z)\right) \\\\\quad k(z) &=& z^2 & \Rightarrow & k'(z) &=& 2z \\\\f'(z) &=& -\dfrac{3}{20}\left(1+\cos\left(z^2\right)\right)^{-\frac{1}{2}}\cdot \left(-\sin\left(z^2\right)\right)\cdot 2z \\\\&=& \dfrac{3z\cdot \sin\left(z^2\right)}{10\left(1+\cos\left(z^2\right)\right)^{\frac{1}{2}}} \\\\&=& \dfrac{3z\cdot \sin\left(z^2\right)}{10\sqrt{1+\cos(z^2)}}\end{array}$

18)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R}^+_0 \\\\f(x) &=& \sqrt{e^{\sqrt{x}-t}} \\&=& \left(e^{\sqrt{x}-t}\right)^{\frac{1}{2}} \\\\\quad g(h(k(x))) &=& \left(h\left(k(x)\right)\right)^{\frac{1}{2}} & \Rightarrow & g'(h(k(x))) &=& \dfrac{1}{2}\left(h\left(k(x)\right)\right)^{-\frac{1}{2}} \\\quad h(k(x)) &=& e^{k(x)} & \Rightarrow & h'(k(x)) &=& e^{k(x)} \\\quad k(x) &=& \sqrt{x}-t & \Rightarrow & k'(x) &=& \dfrac{1}{2\sqrt{x}} \\\\f'(x) &=& \dfrac{1}{2}\left(e^{\sqrt{x}-t}\right)^{-\frac{1}{2}} \cdot e^{\sqrt{x}-t}\cdot\dfrac{1}{2\sqrt{x}} \\\\&=& \dfrac{1}{4}\cdot\dfrac{e^{\sqrt{x}-t}}{\sqrt{e^{\sqrt{x}-t}}}\cdot\dfrac{1}{\sqrt{x}} \\\\&=& \dfrac{\sqrt{e^{\sqrt{x}-t}}}{4\sqrt{x}}\end{array}$

19)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R};\;x\ne\frac{-b}{a} \\\\f(x) &=& \dfrac{1}{ax+b} \\&=& (ax+b)^{-1} \\\\\quad g(h(x)) &=& (h(x))^{-1} & \Rightarrow & g'(h(x)) &=& -1(h(x))^{-2} \\\quad h(x) &=& ax+b & \Rightarrow & h'(x) &=& a \\\\f'(x) &=& -1(ax+b)^{-2}\cdot a \\&=& \dfrac{-a}{(ax+b)^2}\end{array}$

20)
$\begin{array}{lclcrcl}\quad\mathbb{D} &=& \mathbb{R} \\\\f(x) &=& \tan\left(c\cdot \sin(x)\right) \\\\\quad g(h(x)) &=& \tan\left(h(x)\right) & \Rightarrow & g'(h(x)) &=& \dfrac{1}{\cos^2\left(h(x)\right)} \\\quad h(x) &=& c\cdot \sin(x) & \Rightarrow & h'(x) &=& c\cdot \cos(x) \\\\f'(x) &=& \dfrac{1}{\cos^2\left(c\cdot\sin(x)\right)}\cdot c\cdot \cos(x) \\\\&=& \dfrac{c\cdot \cos(x)}{\cos^2\left(c\cdot\sin(x)\right)}\end{array}$

6. Aufgabe

1)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\{-2\}} \cr \cr f(x) &=& \dfrac{1}{2x+4} \cr \cr \quad u(x) &=& 1 & \Rightarrow & u'(x) &=& 0 \cr \quad v(x) &=& 2x+4 & \Rightarrow & v'(x) &=& 2\cr \cr f'(x) &=& \dfrac{0 \cdot (2x+4)-1 \cdot 2}{(2x+4)^2} \cr \cr &=& \dfrac{-2}{4x^2+16x+16} \cr \cr &=& -\dfrac{2}{2(2x^2+8x+8)} \cr \cr &=& -\dfrac{1}{2x^2+8x+8} \end{array}$

Vorgehen: Quotientenregel

2)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x) &=& \cos(7x+8) \cr \cr \quad g(h(x)) &=& \cos(h(x)) & \Rightarrow & g'(h(x)) &=& -\sin(h(x)) \cr \quad h(x) &=& 7x+8 & \Rightarrow & h'(x) &=& 7 \cr \cr f'(x) &=& -\sin(7x+8) \cdot 7 \cr &=& -7 \sin(7x+8) \end{array}$

Vorgehen: Kettenregel

3)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x) &=& (x^2+1)\sin(x) \cr \cr \quad u(x) &=& x^2+1 & \Rightarrow & u'(x) &=& 2x \cr \quad v(x) &=& \sin(x) & \Rightarrow & v'(x) &=& \cos(x) \cr \cr f'(x) &=& 2x\sin(x)+(x^2+1)\cos(x) \end{array}$

Vorgehen: Produktregel

4)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x) &=& 12xe^{x+10} \cr \cr \quad u(x) &=& 12x & \Rightarrow & u'(x) &=& 12 \cr \quad v(h(x)) &=& e^{h(x)} & \Rightarrow & v'(h(x)) &=& e^{h(x)} \cr \quad h(x) &=& x+10 & \Rightarrow & h'(x) &=& 1 \cr \cr f'(x) &=& 12 \cdot e^{x+10} + 12x e^{x+10} \cdot 1 \cr &=& 12e^{x+10}(1+x) \end{array}$

Vorgehen: Produktregel, Kettenregel im 2. Faktor

5)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}^+_0 \cr \cr f(x) &=& e^{\sqrt{x}} \cr \cr &=& e^{x^{\frac{1}{2}}} \cr \cr \quad g(h(x)) &=& e^{h(x)} & \Rightarrow & g'(h(x)) &=& e^{h(x)} \cr \quad h(x) &=& x^{\frac{1}{2}} & \Rightarrow & h'(x) &=& \dfrac{1}{2}x^{-\frac{1}{2}} \cr \cr f'(x) &=& e^{x^{\frac{1}{2}}} \cdot \dfrac{1}{2}x^{-\frac{1}{2}} \cr \cr &=& \dfrac{1}{2}x^{-\frac{1}{2}} e^{x^{\frac{1}{2}}} \cr \cr &=& \dfrac{1}{2\sqrt{x}} e^{\sqrt{x}} \end{array}$

Vorgehen: Kettenregel

6)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}\setminus_{\{1\}} \cr \cr f(x) &=& \dfrac{x^2+1}{x^3-1} \cr \cr \quad u(x) &=& x^2+1 & \Rightarrow & u'(x) &=& 2x \cr \quad v(x) &=& x^3-1 & \Rightarrow & v'(x) &=& 3x^2 \cr \cr f'(x) &=& \dfrac{2x \cdot (x^3-1)-(x^2+1) \cdot 3x^2}{(x^3-1)^2} \cr\cr &=& \dfrac{2x^4-2x-3x^4-3x^2}{x^6-2x^3+1} \cr\cr &=& \dfrac{-x^4-3x^2-2x}{x^6-2x^3+1} \end{array}$

Vorgehen: Quotientenregel

7)
$\begin{array}{rcl}\quad\mathbb{D}&=&\mathbb{R}^+ \cr \cr f(x)&=&\ln(x)+7^x+\sin(x)+5 \cr\cr\cr f'(x)&=&\dfrac{1}{x}+7^x\cdot\ln\left(7\right)+\cos(x)\end{array}$

Vorgehen: Hier wird keine der komplexeren Ableitungsregeln benötigt. Jeder Summand kann für sich abgeleitet werden.

8)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x)&=&\cos(x^2) \cr\cr \quad g(h(x)) &=&\cos(h(x)) & \Rightarrow & g'(h(x)) &=& -\sin(h(x)) \cr \quad h(x) &=& x^2 & \Rightarrow & h'(x) &=& 2x \cr \cr f'(x)&=& -\sin(x^2) \cdot 2x \cr &=& -2x \cdot \sin(x^2)\end{array}$

Vorgehen: Kettenregel

9)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x)&=&\cos^2(x) \cr\cr \quad g(h(x)) &=& (h(x))^2 & \Rightarrow & g'(h(x)) &=& 2h(x) \cr \quad h(x) &=& \cos(x) & \Rightarrow & h'(x) &=& -\sin(x) \cr \cr f'(x) &=& 2\cdot \cos(x) \cdot \left( -\sin(x) \right) \cr &=&-2\sin(x)\cos(x) \end{array}$

Vorgehen: Kettenregel

Bemerkung: $\cos^2(x) = \left[ \cos(x) \right]^2$

10)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x)&=&x^2 \cdot 10^x \cr\cr \quad u(x) &=& x^2 & \Rightarrow & u'(x) &=& 2x \cr \quad v(x) &=& 10^x & \Rightarrow & v'(x) &=& 10^x\cdot\ln\left(10\right) \cr \cr f'(x) &=& 2x \cdot 10^x + x^2 \cdot10^x\cdot\ln\left(10\right) \cr &=& 10^x\left(2x+x^2\ln\left(10\right)\right) \end{array}$

Vorgehen: Produktregel

11)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\left\{x\in\mathbb{R}\vert x\neq\pm\sqrt{\frac{\pi}{2}+k\pi} , k\in\mathbb{Z}\right\} \cr \cr f(x)&=&\dfrac{\sin(x)}{\cos(x^2)} \cr\cr \quad u(x) &=& \sin(x) & \Rightarrow & u'(x) &=& \cos(x) \cr \quad v(h(x)) &=& \cos(h(x)) & \Rightarrow & v'(x) &=& -\sin(h(x)) \cr \quad h(x) &=& x^2 & \Rightarrow & h'(x) &=& 2x \cr \cr f'(x) &=& \dfrac{\cos(x) \cdot \cos(x^2) - \sin(x) \cdot \left( -\sin(x^2) \right) \cdot 2x}{ \left( \cos(x^2) \right)^2 } \cr \cr &=&\dfrac{\cos(x) \cdot \cos(x^2)+2x \cdot \sin(x) \cdot \sin(x^2)}{\cos^2(x^2)}\end{array}$

Vorgehen: Quotientenregel, Kettenregel im Nenner

12)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R}^+ \cr \cr f(x)&=&\ln\left(\dfrac{1}{x}\right) \cr\cr \quad g(h(x)) &=& \ln(h(x)) & \Rightarrow & g'(x) &=& \dfrac{1}{h(x)} \cr \quad h(x) &=& \dfrac{1}{x} = x^{-1} & \Rightarrow & h'(x) &=& -1x^{-2} = -\dfrac{1}{x^2} \cr\cr f'(x) &=& \genfrac{}{}{1pt}{0}{1}{\dfrac{1}{x}} \cdot \left(-\dfrac{1}{x^2} \right) \cr\cr &=& -x \cdot \dfrac{1}{x^2} \cr\cr &=&-\dfrac{1}{x}\end{array}$

Vorgehen: Kettenregel

13)
$\begin{array}{rcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x)&=&\tan(x)-\cos(x) \cr\cr f'(x)&=&\dfrac{1}{\cos^2(x)}+\sin(x)\end{array}$

Vorgehen: Hier wird keine der komplexeren Ableitungsregeln benötigt.

14)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x) &=& \lg(x^2+2) \cr\cr \quad g(h(x)) &=& \lg(h(x)) & \Rightarrow & g'(h(x)) &=& \dfrac{1}{h(x) \cdot \ln(10)} \cr \quad h(x) &=& x^2+2 & \Rightarrow & h'(x) &=& 2x \cr\cr f'(x) &=& \dfrac{1}{\left(x^2+2 \right) \cdot \ln(10)} \cdot 2x \cr\cr &=& \dfrac{2x}{\ln(10) \cdot (x^2+2)} \end{array}$

Vorgehen: Kettenregel

Bemerkung: $\lg$ ist der dekadische Logarithmus, d. h. seine Basis ist 10.

15)
$\begin{array}{rcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x) &=& \dfrac{3x^2-2x+1}{2} \cr\cr &=& \dfrac{3}{2}x^2-x+\dfrac{1}{2} \cr\cr\cr f'(x) &=& 3x-1\end{array}$

Vorgehen: Hier wird keine der komplexeren Ableitungsregeln benötigt.

Bemerkung: Bei dieser Funktion wird nicht die Quotientenregeln benötigt, auch wenn dies vielleicht auf den ersten Blick so aussieht. Da aber im Nenner keine Variable, sondern nur eine Zahl enthalten ist, helfen die "normalen" Regeln der Bruchrechnung weiter.

16)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x) &=& e^{-\frac{x^2}{2}} \cr\cr \quad g(h(x)) &=& e^{h(x)} & \Rightarrow & g'(h(x)) &=& e^{h(x)} \cr \quad h(x) &=& -\dfrac{x^2}{2} & \Rightarrow & h'(x) &=& -x \cr\cr f'(x) &=& e^{-\frac{x^2}{2}} \cdot \left( -x \right) \cr &=& -x \cdot e^{-\frac{x^2}{2}} \end{array}$

Vorgehen: Kettenregel

17)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x) &=& x \cdot e^{-5x^2} \cr\cr \quad u(x) &=& x & \Rightarrow & u'(x) &=& 1 \cr \quad v(h(x)) &=& e^{h(x)} & \Rightarrow & v'(h(x)) &=& e^{h(x)} \cr \quad h(x) &=& -5x^2 & \Rightarrow & h'(x) &=& -10x \cr\cr f'(x) &=& 1 \cdot e^{-5x^2} + x\cdot e^{-5x^2} \cdot \left( -10x \right) \cr &=& e^{-5x^2} - 10x^2 \cdot e^{-5x^2} \cr &=& e^{-5x^2} \cdot \left(1 - 10x^2\right) \end{array}$

Vorgehen: Produktregel, Kettenregel im 2. Faktor

18)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\{x\in\mathbb{R}\vert x\neq\pm 1\} \cr \cr f(x) &=& \dfrac{2}{2x^2-2} \cr\cr &=& 2(2x^2-2)^{-1} \cr\cr \quad g(h(x)) &=& 2(h(x))^{-1} & \Rightarrow & g'(h(x)) &=& -2(h(x))^{-2} = \dfrac{-2}{h(x)^2} \cr \quad h(x) &=& 2x^2-2 & \Rightarrow & h'(x) &=& 4x \cr\cr f'(x) &=& \dfrac{-2}{\left( 2x^2-2 \right)^2} \cdot 4x \cr\cr &=& \dfrac{-8x}{4x^4-8x^2+4} \cr\cr &=& \dfrac{-2x}{x^4-2x^2+1} \cr\cr &=& -\dfrac{2x}{(x^2-1)^2} \end{array}$

Vorgehen: Kettenregel

Bemerkung: Man könnte diese Funktion natürlich auch mit der Quotientenregel ableiten.

19)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\mathbb{R} \cr \cr f(x) &=& (3x^3+3)^{27} \cr\cr \quad g(h(x)) &=& (h(x))^{27} & \Rightarrow & g'(h(x)) &=& 27(h(x))^{26} \cr \quad h(x) &=& 3x^3+3 & \Rightarrow & h'(x) &=& 9x^2 \cr\cr f'(x) &=& 27\left( 3x^3+3 \right)^{26}\cdot9x^2 \cr &=& 243x^2 \cdot (3x^3+3)^{26} \end{array}$

Vorgehen: Kettenregel

20)
$\begin{array}{lclcrcl}\quad\mathbb{D}&=&\{x,a,b,c\in\mathbb{R}\vert ax^2+bx+c>0\} \cr \cr f(x)&=&\ln\left(ax^3+bx^2+c\right) \cr\cr \quad g(h(x)) &=& \ln(h(x)) & \Rightarrow & g'(h(x)) &=& \dfrac{1}{h(x)} \cr \quad g(x) &=& ax^3+bx^2+c & \Rightarrow & g'(x) &=& 3ax^2+2bx \cr \cr \cr f'(x)&=&\dfrac{1}{ax^3+bx^2+c}\cdot\left(3ax^2+2bx\right) \cr \cr &=&\dfrac{3ax^2+2bx}{ax^3+bx^2+c}\end{array}$

Vorgehen: Kettenregel

7. Aufgabe

1)
1. Schritt: potenzielle x-Werte für die Extrempunkte berechnen
$\begin{array}{rclll} \mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& 4x-12 \cr \cr 0 &=& 4x-12 & \vert & -4x \cr -4x &=& -12 & \vert & :(-4) \cr x &=& 3\end{array}$

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunkts ermitteln
$\begin{array}{rclll} f''(x) &=& 4 \cr \cr f''(3) &=& 4 & > & 0 \quad \Rightarrow \text{Tiefpunkt} \end{array}$

3. Schritt: Funktionswert ausrechnen
$\begin{array}{rclll} f(x) &=& 2x^2-12x+24 \cr\cr f(3) &=& 2\cdot 3^2-12\cdot 3+24 &=& 6 \end{array}$

Ergebnis: Die Funktion hat bei $\left(3\mid 6\right)$ einen Tiefpunkt.

2)
1. Schritt: potenzielle x-Werte für die Extrempunkte berechnen
$\begin{array}{rclll} \mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& -5x+10 \cr \cr 0 &=& -5x+10 & \vert & +5x \cr 5x &=& 10 & \vert & :5 \cr x &=& 2 \end{array}$

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunkts ermitteln
$\begin{array}{rclll} f''(x) &=& -5 \cr\cr f''(2)&=& -5 & < & 0 \quad \Rightarrow \text{Hochpunkt} \end{array}$

3. Schritt: Funktionswert berechnen
$\begin{array}{rclll} f(x) &=& -\dfrac{5}{2}x^2+10x+\dfrac{3}{8} \cr\cr f(2) &=&-\dfrac{5}{2} \cdot 2^2+10\cdot 2+\dfrac{3}{8} &=& \dfrac{83}{8} \end{array}$

Ergebnis: Die Funktion hat bei $\left(2\mid \dfrac{83}{8}\right)$ einen Hochpunkt.

3)
1. Schritt: potenzielle x-Werte für die Extrempunkte berechnen
$\begin{array}{rclll} \mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& 160x-16 \cr \cr 0 &=& 160x-16 & \vert & -160x \cr -160x &=& -16 & \vert & :(-160) \cr x &=& \dfrac{1}{10} \end{array}$

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunkts ermitteln
$\begin{array}{rclll} f''(x) &=& 160 \cr\cr f''\left(\dfrac{1}{10}\right)&=& 160 & > & 0\quad \Rightarrow \text{Tiefpunkt} \end{array}$

3. Schritt: Funktionswert berechnen
$\begin{array}{rclll} f(x) &=& 80x^2-16x+23 \cr\cr f \left(\dfrac{1}{10}\right) &=& 80\cdot \left(\dfrac{1}{10}\right)^2-16\cdot \dfrac{1}{10}+23 &=& \dfrac{111}{5} \end{array}$

Ergebnis: Die Funktion hat bei $\left(\dfrac{1}{10}\mid \dfrac{111}{5}\right)$ einen Hochpunkt.

4)
1. Schritt: potenzielle x-Werte für die Extrempunkte berechnen
$\begin{array}{rclll} \mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& x^2+4x-12 \cr \cr 0 &=& x^2+4x-12 \cr x_{1,2} &=& -\dfrac{4}{2} \pm \sqrt{\left(-\dfrac{4}{2}\right)^2-(-12)} \cr x_{1,2} &=& -2 \pm \sqrt{16} \cr\cr x_1 &=& -2+4 \quad = \quad 2 \cr x_2 &=& -2-4 \quad = \quad -6\end{array}$

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunkts ermitteln
$\begin{array}{rclll} f''(x) &=& 2x+4 \cr\cr f''(2) &=& 2 \cdot 2+4 \quad = \quad 8 & > & 0\quad \Rightarrow \text{Tiefpunkt} \cr f''(-6) &=& 2 \cdot (-6)+4 \quad = \quad -8 & < & 0\quad \Rightarrow \text{Hochpunkt}\end{array}$

3. Schritt: Funktionswerte berechnen
$\begin{array}{rclll}f(x) &=& \dfrac{1}{3}x^3+2x^2-12x+6 \cr\cr f \left(2\right) &=&\dfrac{1}{3} \cdot 2^3+2\cdot 2^2-12 \cdot 2+6 &=& -\dfrac{22}{3} \cr f \left(-6\right) &=&\dfrac{1}{3} \cdot (-6)^3+2\cdot (-6)^2-12 \cdot (-6)+6 &=& 78 \end{array}$

Ergebnis: Die Funktion hat bei $\left(2\mid -\dfrac{22}{3}\right)$ einen Tiefpunkt und bei $\left(-6\mid 78\right)$ einen Hochpunkt.

Bemerkung: Wer noch mal nachschauen möchte, wie das mit dem Lösen quadratischer Gleichungen war, findet hier Informationen.

5)
1. Schritt: potenzielle x-Werte für die Extrempunkte berechnen
$\begin{array}{crclll} & \mathbb{D} &=& \mathbb{R} \cr\cr & f'(x) &=& 2x^3-6x \cr & 0 &=& 2x^3-6x \cr & 0 &=& x\left(2x^2-6\right) &\vert & \text{Satz vom Nullprodukt} \cr \text{Faktor 1:} & x_1 &=& 0 \cr\cr \text{Faktor 2:} & 0 &=& 2x^2-6 &\vert & -2x^2 \cr & -2x^2 &=& -6 & \vert & :(-2) \cr & x^2 &=& 3 \cr & x_2 &=& \sqrt{3} \cr & x_3 &=& -\sqrt{3} \end{array}$

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunkts ermitteln
$\begin{array}{rclll} f''(x) &=& 6x^2-6 \cr\cr f''\left(-\sqrt{3}\right) &=&6 \cdot\left(-\sqrt{3}\right)^2-6 \quad = \quad 12 & > & 0\quad \Rightarrow \text{Tiefpunkt} \cr f''(0) &=& 6 \cdot 0^2-6 \quad = \quad -6 & < & 0\quad \Rightarrow \text{Hochpunkt} \cr f''\left(\sqrt{3}\right) &=&6 \cdot \sqrt{3}^2-6 \quad = \quad 12 & > & 0\quad \Rightarrow \text{Tiefpunkt} \end{array}$

3. Schritt: Funktionswerte berechnen
$\begin{array}{rclll}f(x) &=& \dfrac{1}{2}x^4-3x^2+1 \cr\cr f\left(-\sqrt{3}\right) &=&\dfrac{1}{2}\cdot\left(-\sqrt{3}\right)^4-3\cdot \left(-\sqrt{3}\right)^2+1 &=& -\dfrac{7}{2} \cr\cr f\left(0\right) &=&\dfrac{1}{2}\cdot0^4-3\cdot 0^2+1 &=& 1 \cr\cr f\left(\sqrt{3}\right) &=&\dfrac{1}{2}\cdot\sqrt{3}^4-3\cdot\sqrt{3}^2+1 &=& -\dfrac{7}{2} \end{array}$

Ergebnis: Die Funktion hat bei $\left(-\sqrt{3}\mid -\dfrac{7}{2}\right)$ einen Tiefpunkt, bei $\left(0\mid 1\right)$ einen Hochpunkt und $\left(\sqrt{3}\mid -\dfrac{7}{2}\right)$ einen Tiefpunkt.

6)
Vorab: Ableitungen berechnen
$\begin{array}{rclll} \mathbb{D} &=& \mathbb{R}\setminus_{\left\{1\right\}} \cr\cr f'(t) &=& \dfrac{\left(4t^3-9t^2+5\right)(t-1)-\left(t^4-3t^3+5t-5\right)\cdot 1}{(t-1)^2} \cr\cr &=& \dfrac{3t^4-10t^3+9t^2}{(t-1)^2} \cr\cr\cr f''(t) &=& \dfrac{\left(12t^3-30t^2+18t\right)(t-1)^2-\left(3t^4-10t^3+9t^2\right)\cdot 2(t-1) \cdot 1}{(t-1)^4} \cr\cr &=& \dfrac{\left(12t^3-30t^2+18t\right)(t-1)-\left(3t^4-10t^3+9t^2\right)\cdot 2}{(t-1)^3} \cr\cr &=& \dfrac{6t^4-22t^3+30t^2-18t}{(t-1)^3} \end{array}$

Bemerkung: Bei der 2. Ableitung ist darauf zu achten, dass im Rahmen der Anwendung der Quotientenregel für die Ableitung des Nennerterms im Zähler die Kettenregel zu nutzen ist. Das erklärt die $\cdot 1$ am Ende des Zählers ...

1. Schritt: potenzielle x-Werte für Extrempunkte berechnen
$\begin{array}{rclll} f'(t) &=& \dfrac{3t^4-10t^3+9t^2}{(t-1)^2} \cr \cr 0 &=& \dfrac{t^2\left(3t^2-10t+9\right)}{(t-1)^2} \cr 0 &=& t^2\left(3t^2-10t+9\right) \cr t &=& 0 \cr 3t^2-10t+9 &=& 0 &\vert & :3 \cr t^2-\dfrac{10}{3}t+3 &=& 0 &\vert & \text{p-q-Formel} \cr t_{1,2} &=& \dfrac{5}{3}\pm\sqrt{\left(\dfrac{5}{3}\right)^2-3} \cr t_{1,2} &=& \dfrac{5}{3}\pm\sqrt{-\dfrac{2}{9}}\end{array}$

Bemerkung: Ein Bruch kann nur dann den Wert $0$ annehmen, wenn sein Zähler $0$ ist. Insofern müssen wir uns nach dem Nullsetzen nur noch um den Zähler kümmern. 

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunktes ermitteln
$\begin{array}{rclll} f''(t) &=& \dfrac{6t^4-22t^3+30t^2-18t}{(t-1)^3} \cr\cr f''(0) &=& \dfrac{6 \cdot 0^4-22 \cdot 0^3+30 \cdot 0^2-18\cdot 0}{(0-1)^3} \quad = \quad 0\end{array}$

Ergebnis: Mit den Methoden, die in diesem Lernmodul gezeigt wurden, können wir (leider) keine Aussage treffen, was bei dem gefundenen x-Wert mit der Funktion los ist. Mithilfe anderer Verfahren findet man heraus, dass diese Funktion bei $x=0$ einen Sattelpunkt hat. Diese Methoden werden Sie - wenn nötig - im Studium kennenlernen.

Bemerkung: Die Divisionen durch $(t-1)^2$, $(t-1)^3$ und $(t-1)^4$ sind hier ohne Einschränkungen möglich, weil $t=1 \not\in \mathbb{D}$. Eine Division durch $0$ kann also nicht passieren.

7)
Vorab: Ableitungen berechnen
$\begin{array}{rclll} \mathbb{D} &=& \left]\dfrac{8-\sqrt{70}}{6};\dfrac{8+\sqrt{70}}{6}\right[ \cr\cr f(x) &=& \left(-6x^2+16x+1\right)^{\frac{1}{2}} \cr\cr\cr f'(x) &=& \frac{1}{2}\left(-6x^2+16x+1\right)^{-\frac{1}{2}}\cdot (-12x+16) \cr\cr &=& \dfrac{-6x+8}{\sqrt{-6x^2+16x+1}} \cr\cr &=& (-6x+8)\left(-6x^2+16x+1\right)^{-\frac{1}{2}} \cr\cr\cr f''(x) &=& -6\cdot\left(-6x^2+16x+1\right)^{-\frac{1}{2}} + (-6x+8)\cdot\left(-\frac{1}{2}\right)\left(-6x^2+16x+1\right)^{-\frac{3}{2}}\cdot (-12x+16) \cr\cr &=& \dfrac{-6}{\left(-6x^2+16x+1\right)^{\frac{1}{2}}} + \dfrac{(-6x+8)\left(-\frac{1}{2}\right)(-12x+16)}{\left(-6x^2+16x+1\right)^{\frac{3}{2}}} \cr\cr &=& \dfrac{-6\left(-6x^2+16x+1\right)}{\left(-6x^2+16x+1\right)^{\frac{1}{2}}\left(-6x^2+16x+1\right)} + \dfrac{(-6x+8)\left(-\frac{1}{2}\right)(-12x+16)}{\left(-6x^2+16x+1\right)^{\frac{3}{2}}} \cr\cr &=& \dfrac{-70}{\left(-6x^2+16x+1\right)^{\frac{3}{2}}} \end{array}$

Bemerkung: Bei der 1. Ableitung die Kettenregel nicht vergessen ... Unter der Wurzel steht ja eine Polynomfunktion. Bei der 2. Ableitung werden die Produkt- und die Kettenregel benötigt. Es ist beim Ableiten häufig einfacher, Wurzeln, die im Nenner eines Bruches stehen, in die Potenzschreibweise umzuformen, anstatt die Quotientenregel zu verwenden.

1. Schritt: potenzielle x-Werte für Extrempunkte berechnen
$\begin{array}{rclll} f'(x) &=& \dfrac{-6x+8}{\sqrt{-6x^2+16x+1}} \cr \cr 0 &=& \dfrac{-6x+8}{\sqrt{-6x^2+16x+1}} \cr 0 &=& -6x+8 &\vert & +6x \cr 6x &=& 8 &\vert & :6 \cr \cr x &=& \dfrac{4}{3}\end{array}$

Bemerkung: Ein Bruch kann nur dann den Wert $0$ annehmen, wenn sein Zähler $0$ ist. Insofern müssen wir uns nach dem Nullsetzen nur noch um den Zähler kümmern.

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunktes ermitteln
$\begin{array}{rclll} f''(x) &=& \dfrac{-70}{(-6x^2+16x+1)^{\frac{3}{2}}} \cr\cr f''\left(\dfrac{4}{3}\right) &=& \dfrac{-70}{\left(-6 \cdot \left(\dfrac{4}{3}\right)^2+16 \cdot \dfrac{4}{3}+1\right)^{\frac{3}{2}}} \quad \approx \quad -1{,}76 \quad < \quad 0 & & \Rightarrow \text{Hochpunkt}\end{array}$

3. Schritt: Funktionswerte berechnen
$\begin{array}{rclll} f(x) &=& \sqrt{-6x^2+16x+1} \cr \cr f\left(\dfrac{4}{3}\right) &=& \sqrt{-6 \cdot \left(\dfrac{4}{3}\right)^2+16 \cdot \dfrac{4}{3}+1} &=& \dfrac{\sqrt{105}}{3} \end{array}$

Ergebnis: Die Funktion hat bei $\left(\dfrac{4}{3}\mid \dfrac{\sqrt{105}}{3} \right)$ einen Hochpunkt.

Bemerkung: Die Divisionen durch $\left(-6x^2+16x+1\right)$, $\sqrt{-6x^2+16x+1}$ und $\left(-6x^2+16x+1\right)^{\frac32}$ sind hier ohne Einschränkungen möglich, weil $x=\dfrac{8-\sqrt{70}}{6} \not\in \mathbb{D}$ und $x=\dfrac{8+\sqrt{70}}{6} \not\in\mathbb{D}$. Eine Division durch $0$ kann also nicht passieren.

8)
Vorab: Ableitungen berechnen
$\begin{array}{rclll} \mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& e^{0{,}1x^2-8x-6{,}3}\cdot \left(0{,}2x-8\right) \cr\cr &=& \left(\dfrac{x}{5}-8\right)e^{0{,}1x^2-8x-6{,}3} \cr\cr\cr f''(x) &=& \dfrac{1}{5}e^{0{,}1x^2-8x-6{,}3} +\left(\dfrac{x}{5}-8\right)e^{0{,}1x^2-8x-6{,}3}\cdot\left(\dfrac{x}{5}-8\right) \cr\cr &=& \left(\dfrac{1}{5}+\left(\dfrac{x}{5}-8\right)\left(\dfrac{x}{5}-8\right)\right)e^{0{,}1x^2-8x-6{,}3} \cr\cr &=& \dfrac{\left(x^2-80x+1.605\right)}{25}e^{0{,}1x^2-8x-6{,}3} \end{array}$

Bemerkung: Bei der 1. Ableitung die Kettenregel nicht vergessen ... Im Exponenten steht ja eine Polynomfunktion. Bei der 2. Ableitung werden die Produkt- und die Kettenregel benötigt.

1. Schritt: potenzielle x-Werte für Extrempunkte berechnen
$\begin{array}{rclll} f'(x) &=& \left(\dfrac{x}{5}-8\right)e^{0{,}1x^2-8x-6{,}3} \cr \cr 0 &=& \left(\dfrac{x}{5}-8\right)e^{0{,}1x^2-8x-6{,}3} &\vert & :e^{0{,}1x^2-8x-6{,}3} \cr \cr 0 &=& \dfrac{x}{5}-8 &\vert & -\dfrac{x}{5} \cr -\dfrac{x}{5} &=& -8 &\vert & \cdot (-5) \cr x &=& 40 \end{array}$

Bemerkung: Da Exponentialfunktionen nie den Wert $0$ annehmen, kann hier bedenkenlos durch diesen Teil geteilt werden. Das vereinfacht die Sache doch erheblich ...

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunktes ermitteln
$\begin{array}{rclll} f''(x) &=& \dfrac{\left(x^2-80x+1.605\right)}{25}e^{0{,}1x^2-8x-6{,}3} \cr\cr f''(40) &=& \dfrac{\left(40^2- 80 \cdot 40+1.605\right)}{25}e^{0{,}1 \cdot 40^2-8 \cdot 40-6{,}3} \quad = \quad \dfrac{1}{5} e^{-166{,}3} \quad > \quad 0 & & \Rightarrow \text{Tiefpunkt}\end{array}$

3. Schritt: Funktionswerte berechnen
$\begin{array}{rclll} f(x) &=& e^{0{,}1x^2-8x-6{,}3} \cr \cr f(40) &=& e^{0{,}1 \cdot 40^2-8 \cdot 40-6{,}3} &=& e^{-166{,}3} \end{array}$

Ergebnis: Die Funktion hat bei $\left(40 \mid e^{-166{,}3} \right)$ einen Tiefpunkt.

9)
Vorab: Ableitungen berechnen
$\begin{array}{rclll} \mathbb{D} &=& \mathbb{R} \cr\cr f'(x) &=& \dfrac{1}{2 \cdot \ln(10)} \cdot 10^{-8x^4+9x^2} \cdot \left(-32x^3+18x\right)\cdot \ln(10) \cr\cr &=& \left(-16x^3+9x\right) \cdot 10^{-8x^4+9x^2} \cr\cr\cr f''(x) &=& \left(-48x^2+9\right) \cdot 10^{-8x^4+9x^2} + \left(-16x^3+9x\right) \cdot 10^{-8x^4+9x^2} \cdot \left(-32x^3+18x\right)\cdot \ln(10)\cr\cr &=& \left(\left(-48x^2+9\right) + \left(-16x^3+9x\right) \left(-32x^3+18x\right)\ln(10)\right)\cdot 10^{-8x^4+9x^2} \cr\cr &=& \left(\left(512x^6-576x^4+162x^2\right)\ln(10)-48x^2+9\right)\cdot 10^{-8x^4+9x^2} \end{array}$

Bemerkung: Bei der 1. Ableitung die Kettenregel nicht vergessen ... Im Exponenten steht ja eine Polynomfunktion. Bei der 2. Ableitung werden die Produkt- und die Kettenregel benötigt.

1. Schritt: potenzielle x-Werte für Extrempunkte berechnen
$\begin{array}{crclll} & f'(x) &=& \left(-16x^3+9x\right) \cdot 10^{10^{-8x^4+9x^2}} \cr \cr & 0 &=& -x\left(16x^2-9\right) \cdot 10^{10^{-8x^4+9x^2}} &\vert& :10^{10^{-8x^4+9x^2}} \cr & 0 &=& -x\left(16x^2-9\right) &\vert& \text{Satz vom Nullprodukt} \cr\text{Faktor 1:} & x_1 &=& 0 \cr\cr \text{Faktor 2:} & 0 &=& 16x^2-9 &\vert & +9 \cr & 9 &=& 16x^2 &\vert & :16 \cr & \dfrac{9}{16} &=& x^2 &\vert & \pm\sqrt{} \cr & x_2 &=& \dfrac{3}{4} \cr & x_3 &=& -\dfrac{3}{4} \end{array}$

Bemerkung: Auch Exponentialfunktionen zur Basis $10$ können nie den Wert $0$ annehmen. Daher kann bedenkenlos durch diesen Teil geteilt werden, was die Sache wieder deutlich einfacher macht.

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunktes ermitteln
$\begin{array}{rclll} f''(x) &=& \left(\left(512x^6-576x^4+162x^2\right)\ln(10)-48x^2+9\right)\cdot 10^{-8x^4+9x^2} \cr\cr f''\left(-\dfrac{3}{4}\right) &=& \left(\left(512\cdot\left(-\dfrac{3}{4}\right)^6-576\cdot\left(-\dfrac{3}{4}\right)^4+162\cdot\left(-\dfrac{3}{4}\right)^2\right)\ln(10)-48\cdot\left(-\dfrac{3}{4}\right)^2+9\right)\cdot 10^{-8\cdot\left(-\frac{3}{4}\right)^4+9\cdot\left(-\frac{3}{4}\right)^2} \quad \approx \quad -6.116{,}77 \quad < \quad 0 & & \Rightarrow \text{Hochpunkt} \cr\cr f''(0) &=& \left(\left(512\cdot 0^6-576\cdot 0^4+162\cdot 0^2\right)\ln(10)-48\cdot 0^2+9\right)\cdot 10^{-8\cdot 0^4+9\cdot 0^2} \quad = \quad 9 \quad > \quad 0 & & \Rightarrow \text{Tiefpunkt} \cr \cr f''\left(\dfrac{3}{4}\right) &=& \left(\left(512\cdot\left(\dfrac{3}{4}\right)^6-576\cdot\left(\dfrac{3}{4}\right)^4+162\cdot\left(\dfrac{3}{4}\right)^2\right)\ln(10)-48\cdot\left(\dfrac{3}{4}\right)^2+9\right)\cdot 10^{-8\cdot\left(\frac{3}{4}\right)^4+9\cdot\left(\frac{3}{4}\right)^2} \quad \approx \quad -6.116{,}77 \quad < \quad 0 & & \Rightarrow \text{Hochpunkt} \end{array}$

3. Schritt: Funktionswerte berechnen
$\begin{array}{rclll} f(x) &=& \dfrac{1}{2 \cdot \ln(10)} \cdot 10^{-8x^4+9x^2} \cr \cr f\left(-\dfrac{3}{4}\right) &=& \dfrac{1}{2 \cdot \ln(10)} \cdot 10^{-8 \cdot \left(-\frac{4}{3}\right)^4+9 \cdot \left(-\frac{3}{4}\right)^2} &\approx& 73{,}79 \cr\cr f(0) &=& \dfrac{1}{2 \cdot \ln(10)} \cdot 10^{-8 \cdot 0^4+9 \cdot 0^2} &\approx& 0{,}22 \cr \cr f\left(\dfrac{3}{4}\right) &=& \dfrac{1}{2 \cdot \ln(10)} \cdot 10^{-8 \cdot \left(\frac{3}{4}\right)^4+9 \cdot \left(\frac{3}{4}\right)^2} &\approx& 73{,}79 \end{array}$

Ergebnis: Die Funktion hat zwei Hochpunkte bei $\left(\dfrac{3}{4}\mid 73{,}79 \right)$ und $\left(-\dfrac{3}{4}\mid 73{,}79 \right)$ sowie einen Tiefpunkt bei $\left(0 \mid 0{,}22 \right)$.

10)
Vorab: Ableitungen berechnen
$\begin{array}{rclll} \mathbb{D} &=& \left]-2\sqrt{6};0\right[ \cup \left]2\sqrt{6};\infty\right[ \cr\cr f'(x) &=& \dfrac{1}{\frac{1}{2}x^3-12x}\cdot\left(\frac{3}{2}x^2-12\right) \cr\cr &=& \dfrac{3x^2-24}{x^3-24x} \cr\cr\cr f''(x) &=& \dfrac{6x\left(x^3-24x\right)-\left(3x^2-24\right)\left(3x^2-24\right)}{\left(x^3-24x\right)^2}\cr\cr &=& \dfrac{-3x^4-576}{\left(x^3-24x\right)^2} \end{array}$

Bemerkung: Bei der 1. Ableitung die Kettenregel nicht vergessen ... Im Logarithmus steht ja eine Polynomfunktion. Bei der 2. Ableitung wird die Quotientenregel benötigt.

1. Schritt: potenzielle x-Werte für Extrempunkte berechnen
$\begin{array}{rclll} f'(x) &=& \dfrac{3x^2-24}{x^3-24x} \cr \cr 0 &=& \dfrac{3x^2-24}{x^3-24x} \cr 0 &=& 3x^2-24 &\vert & -3x^2 \cr -3x^2 &=& -24 &\vert & :(-3) \cr x^2 &=& 8 &\vert & \pm\sqrt{} \cr \cr x_1 &=& \sqrt{8} & \not\in\mathbb{D} \cr x_2 &=& -\sqrt{8} \end{array}$

Bemerkung: Ein Bruch kann nur dann den Wert $0$ annehmen, wenn sein Zähler $0$ ist. Insofern müssen wir uns nach dem Nullsetzen nur noch um den Zähler kümmern.

2. Schritt: gefundene Stellen überprüfen & ggf. Art des Extrempunktes ermitteln
$\begin{array}{rclll} f''(x) &=& \dfrac{-3x^4-576}{\left(x^3-24x\right)^2} \cr\cr f''\left(-\sqrt{8}\right) &=& \dfrac{-3\cdot\left(-\sqrt{8}\right)^4-576}{\left(\left(-\sqrt{8}\right)^3-24\cdot\left(-\sqrt{8}\right)\right)^2} \quad = \quad -\dfrac{3}{8} \quad < \quad 0 & & \Rightarrow \text{Hochpunkt}\end{array}$

3. Schritt: Funktionswerte berechnen
$\begin{array}{rclll} f(x) &=& \ln\left(\dfrac{1}{2}x^3-12x\right) -15\cr \cr f\left(-\sqrt{8}\right) &=& \ln\left(\dfrac{1}{2} \cdot \left(-\sqrt{8}\right)^3-12 \cdot \left(-\sqrt{8}\right)\right) &\approx& -11{,}88 \end{array}$

Ergebnis: Die Funktion hat bei $\left(-\sqrt{8}\mid -11{,}88 \right)$ einen Hochpunkt.

Bemerkung: Die Divisionen durch $\left(\dfrac12 x^3-12x\right)$, $\left(x^3-24x\right)$ und $\left(x^3-24x\right)^2$ sind hier ohne Einschränkungen möglich, weil $x=-2 \sqrt{6} \not\in \mathbb{D}$, $x=0 \not\in\mathbb{D}$ und $x=2 \sqrt{6} \not\in \mathbb{D}$. Eine Division durch $0$ kann also nicht passieren.

8. Aufgabe

Bemerkung: Die folgenden Aufgaben wirken vielleicht nicht ganz passend für dieses Kapitel. Allerdings ist die Differenzialrechnung nie fern, wenn in der Aufgabe nach dem "größten", "kleinsten", "maximalen" oder "minimalem" Wert gefragt ist ... Sie liefert ja gerade das "Werkzeug", um solche Extremstellen zu berechnen.

1)
Seien $a$ und $b$ die beiden gesuchten Zahlen. Dann gilt:
$a+b=100 \Rightarrow b=100-a$

und

$P(a,b)=a\cdot b$

Setzt man die erste Gleichung in die zweite ein, erhält man:
$\begin{array}{rcl} P(a) &=& a(100-a) \cr &=& 100a-a^2 \end{array}$

Da das Maximum dieser Funktion gesucht ist, leitet man $P(a)$ ab. Der entstehende Term wird nullgesetzt:
$\begin{array}{rclcl} P'(a) &=& 100-2a \cr\cr 0 &=& 100-2a &\vert& +2a \cr 2a &=& 100 &\vert& :2 \cr a &=& 50 \cr \cr b &=& 100-50 = 50 \end{array}$

Nun müssen wir noch überprüfen, ob $a=b=50$ tatsächlich zum größten Produkt aller Zahlenpaare, deren Summe $100$ ist, führt. Aus unserer Rechnung können wir bislang nur ablesen, dass $a=b=50$ entweder zum größten oder zum kleinsten Produkt führt (die erste Ableitung liefert ja keine Informationen über die Art des Extrempunkts ...). Dafür kann man einfach einige dieser Produkte ausrechnen:

Ergebnis: Von allen Zahlenpaaren, deren Summe $100$ ist, hat $a=b=50$ das größte Produkt.

2)
Seien $a$ und $b$ die Seitenlängen des Rechtecks. Dann gilt:
$\begin{array}{rclcl} U &=& 2a+2b \cr 36 &=& 2a+2b &\vert& -2b \cr 36-2b &=& 2a &\vert& :2 \cr 18-b &=& a \end{array}$

und

$A(a,b) = a\cdot b$

Setzt man die erste Gleichung in die zweite ein, erhält man:
$\begin{array}{rcl} A(b) &=& (18-b)b \cr &=& 18b-b^2 \end{array}$

Da das Maximum dieser Funktion gesucht ist, leitet man $A(b)$ ab. Der entstehende Term wird nullgesetzt:
$\begin{array}{rclcl} A'(b) &=& 18-2b \cr\cr 0 &=& 18-2b &\vert& +2b \cr 2b &=& 18 &\vert& \cdot \dfrac{1}{2} \cr b &=& 9 \cr \cr a &=& 18-9 = 9 \end{array}$

Wieder müssen wir nun überprüfen, ob $a=b=9$ tatsächlich zu einem Rechteck des Umfangs $36$ mit maximalem Flächeninhalt führt.

 
Ergebnis: Von allen Paaren von Rechtecksseiten, die zusammen $36$ lang sind, hat $a=b=9$ den größten Flächeninhalt. Es handelt sich also um ein Quadrat.

3)


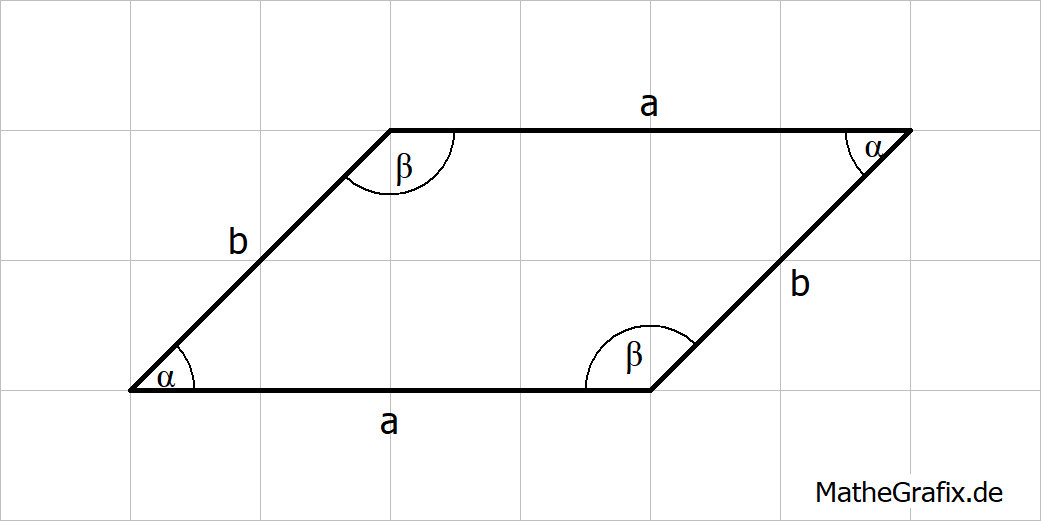
Für den Flächeninhalt eines Parallelogramms gilt: $A = ab \sin\left(\alpha\right)$.
Da die Seitenlängen $a$ und $b$ vorgegeben sind (auch wenn wir sie nicht kennen), hängt der Flächeninhalt in dieser Aufgabe also nur vom Winkel $\alpha$ ab. Wir erhalten die Funktion:
$A\left(\alpha\right) = ab \sin\left(\alpha\right)$

Da das Maximum dieser Funktion gesucht ist, leitet man $A\left(\alpha\right)$ ab. Der entstehende Term wird nullgesetzt:
$\begin{array}{rclcl} A'\left(\alpha\right) &=&ab \cos\left(\alpha\right) \cr\cr 0 &=&ab \cos\left(\alpha\right) &\vert& :ab \cr 0 &=&\cos\left(\alpha\right) \end{array}$
Bitte beachten Sie beim Ableiten, dass $a$ und $b$ positive Konstanten sind. Wären sie negativ oder $0$, ergäbe sich ja kein Parallelogramm ... Daher dürfen wir hier auch ohne Einschränkungen durch $ab$ teilen.

Gesucht sind also die Werte für $\alpha$, für die $\cos\left(\alpha\right)$ den Wert $0$ annimmt. Davon gibt es - wie im Kapitel Trigonometrie besprochen - eine ganze Menge ... Nämlich ..., $-\dfrac{3\pi}{2}$, $-\dfrac{\pi}{2}$, $\dfrac{\pi}{2}$, $\dfrac{3\pi}{2}$, ...
Aber nicht alle dieser Winkel kommen hier als Lösung infrage: In der Geometrie sind Winkel größer oder gleich $0$; alle negativen Werte für $\alpha$ scheiden also aus. Wäre auf der anderen Seite $\alpha\geq\pi$, würde sich kein Parallelogramm mehr ergeben, weil alle vier Winkel zusammen dann mehr als $2\pi$ ergeben würden, was nach dem Winkelsummensatz für Vierecke nicht geht. Es bleibt einzig der Wert $\dfrac{\pi}{2}$.

Es gibt noch einen zweiten (kürzeren) Lösungsweg: $A\left(\alpha\right) = ab \sin\left(\alpha\right)$ ist offensichtlich dann am größten, wenn $\sin\left(\alpha\right)$ am größten ist ($a$ und $b$ sind ja fix). Der größte Wert, den der Sinus annehmen kann, ist $1$. Auch das passiert bei vielen Werten, nämlich ..., $-\dfrac{3\pi}{2}$, $-\dfrac{\pi}{2}$, $\dfrac{\pi}{2}$, $\dfrac{3\pi}{2}$, ...
Mithilfe der gleichen Überlegungen wie oben kommt man dazu, dass nur $\dfrac{\pi}{2}$ für diese Aufgaben zu einer Lösung führt. Damit haben wir auch gleich die Bestätigung dafür, dass $\dfrac{\pi}{2}$ zu einem Maximum der Funktion $A\left(\alpha\right) = ab \sin\left(\alpha\right)$ führt.

Ergebnis: Der Flächeninhalt des Parallelogramms ist dann am größten, wenn der Winkel $\alpha=\dfrac{\pi}{2}$ ist. Das heißt, wenn das Parallelogramm zu einem Rechteck wird.