SOS Mathematik
Übersicht:
- Lösung zur 1. Aufgabe
- Lösung zur 2. Aufgabe
- Lösung zur 3. Aufgabe
- Lösung zur 4. Aufgabe
- Lösung zur 5. Aufgabe
- Lösung zur 6. Aufgabe
23.3 Integrale - Lösungen
Eine Bemerkung vorab: Die Musterlösungen in diesem Kapitel sind nicht mehr so ausführlich wie in den meisten anderen Kapiteln. Insbesondere Termumformungen und das Auflösen von einfachen (z. B. linearen oder quadratischen) Gleichungen wurden weggelassen. Wer damit Probleme hat, schaue bitte in den entsprechenden Kapiteln nach.
1. Aufgabe
Hinweis: Bei den folgenden Aufgaben helfen die Potenzgesetze, vor allem die Festlegungen zu gebrochenen und negativen Exponenten, weiter.
11)
Bemerkung: Bitte beachten Sie, dass die Variable hier nicht , sondern
ist! Das bedeutet, dass die Aufgabe einfach mit der Potenzregel zu lösen ist (Die Variable steht ja in der Basis ...).
ist ein griechischer Buchstabe (gesprochen: "xi") - die tauchen ja immer mal wieder in der Mathematik auf ...
12)
Substitution:
Rücksubstitution:
Vorgehen: lineare Substitution
13)
Vorgehen: partielle Integration
14)
Substitution:
Rücksubstitution:
Vorgehen: lineare Substitution
15)
Substitution:
Rücksubstitution:
Vorgehen: Potenzgesetze und lineare Substitution
16)
Das Integral separat betrachtet:
Gesamtergebnis:
Vorgehen: zwei Mal partielle Integration
17)
Vorgehen: partielle Integration
18)
Substitution:
Rücksubstitution:
Vorgehen: Substitution
19)
Bemerkung: Da , muss hier nur eine Konstante integriert werden.
20)
Das Integral separat betrachtet:
Nun das Integral separat betrachtet:
Gesamtergebnis
Vorgehen: drei Mal partielle Integration
2. Aufgabe
2)
Bemerkung: Der letzte Schritt ist nur dazu da, die Summanden in der Reihenfolge der Exponenten beim zu sortieren.
3)
Bemerkung: Die Aufgaben 2) und 3) unterscheiden sich nur in der Integrationsvariable: Bei 2) wird nach integriert, bei 3) nach
. Die jeweils andere Variable wird als Konstante betrachtet.
3. Aufgabe
Gesucht ist nun die Konstante , die dafür sorgt, dass
durch den Punkt
verläuft. Dazu müssen wir
nach
auflösen:
Ergebnis: Die gesuchte Funktion lautet:
Gesucht ist nun die Konstante , die dafür sorgt, dass
durch den Punkt
verläuft. Dazu müssen wir
nach
auflösen:
Ergebnis: Die gesuchte Funktion lautet:
Gesucht ist nun die Konstante , die dafür sorgt, dass
durch den Punkt
verläuft. Dazu müssen wir
nach
auflösen:
Ergebnis: Die gesuchte Funktion lautet:
4)
Die Stammfunktion von ist
.
Gesucht ist nun die Konstante , die dafür sorgt, dass
durch den Punkt
verläuft. Dazu müssen wir
nach
auflösen:
Ergebnis: Die gesuchte Funktion lautet:
5)
Gesucht ist nun die Konstante , die dafür sorgt, dass
durch den Punkt
verläuft. Dazu müssen wir
nach
auflösen:
Bemerkung: Aus dem Kapitel Trigonometrie weiß man, dass .
Ergebnis: Die gesuchte Funktion lautet:
4. Aufgabe
5)
Bemerkung: Bitte achten Sie darauf, dass die Summanden im ersten Schritt vertauscht wurden. Der Summand mit dem höchsten Exponenten steht - wie immer - vorn.
6)
Bemerkung: Die Integrationsvariable ist hier und nicht
! Das heißt,
wird als Konstante, wie eine Zahl, behandelt.
12)
Substitution:
Rücksubstitution:
Vorgehen: lineare Substitution
14)
Substitution:
Rücksubstitution:
Vorgehen: lineare Substitution
15)
Substitution:
Rücksubstitution:
Vorgehen: Substitution
17)
Vorgehen: partielle Integration
19)
Vorgehen: logarithmische Integration
20)
Bemerkung: und
sind hier keine Variablen ...
5. Aufgabe
1)
Es gilt:
Dieser letzte Ausdruck beschreibt den eingeschlossenen Flächeninhalt, der in dieser Aufgabe gleich sein soll. Zu lösen ist also
. Daraus ergibt sich
.
2)
Es gilt:
Dieser letzte Ausdruck beschreibt den eingeschlossenen Flächeninhalt, der in dieser Aufgabe gleich sein soll. Zu lösen ist also
. Daraus ergibt sich
.
Bemerkung 1: Auf diese Lösung hätte man auch ohne Rechnung kommen können (siehe Eigenschaften des Integrals) ... Allerdings ist es durchaus möglich, dass es mehr Lösungen als diese triviale gibt, da das Integral ja den orientierten Flächeninhalt beschreibt. Das bedeutet: Liegt oberhalb der x-Achse genauso viel Fläche wie unterhalb, besitzt das Integral einen Wert von .
Bemerkung 2: Beim Lösen von müssen erst die Brüche gleichnamig gemacht werden. Das ergibt:
. Da ein Bruch aber nur dann
sein kann, wenn der Zähler
ist, reicht es nun,
zu betrachten.
3)
Es gilt:
Dieser letzte Ausdruck beschreibt den eingeschlossenen Flächeninhalt, der in dieser Aufgabe gleich sein soll. Zu lösen ist also
. Daraus ergibt sich
.
4)
Es gilt:
Dieser letzte Ausdruck beschreibt den eingeschlossenen Flächeninhalt, der in dieser Aufgabe gleich sein soll. Zu lösen ist also
. Diese Gleichung hat zwei Lösungen, nämlich
und
.
5)
Es gilt:
Dieser letzte Ausdruck beschreibt den eingeschlossenen Flächeninhalt, der in dieser Aufgabe gleich sein soll. Zu lösen ist also
. Daraus ergibt sich
.
6)
Es gilt:
Dieser letzte Ausdruck beschreibt den eingeschlossenen Flächeninhalt, der in dieser Aufgabe gleich sein soll. Zu lösen ist also
. Daraus ergibt sich
.
6. Aufgabe
1)
Wenn die Fläche zwischen zwei Funktionen zu berechnen ist, sollte man sich zuallererst die Verläufe der Graphen anschauen, also eine Skizze machen.
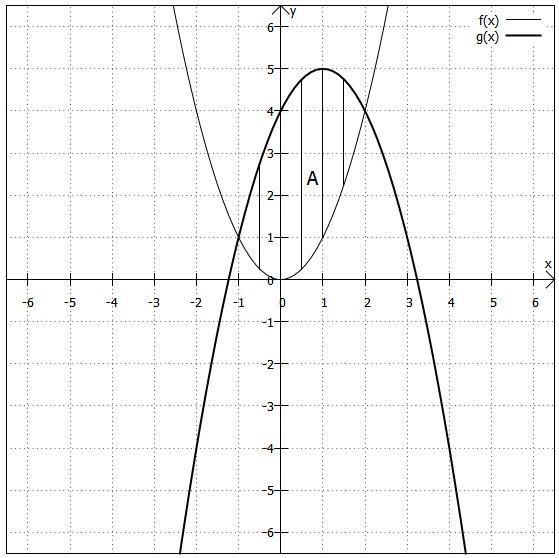
Es ist zu sehen, dass die und
zwei Schnittpunkte haben. Hätten die Funktionen nur einen oder gar keinen Schnittpunkt, könnten sie ja auch keine (komplette) Fläche einschließen. Da die Schnittpunkte die Grenzen des zu berechnenden Integrals bilden, müssen wir sie nun berechnen:
Um die Fläche zwischen den beiden Funktionen zu berechnen, müssen wir die Funktion mit den kleineren Funktionswerten von der anderen abziehen und dann das Integral der Differenzfunktion berechnen, denn die Fläche, die uns interessiert, entsteht dadurch, dass wir die gesamte Fläche unter der "größeren" Funktion nehmen und alles weglassen, was unterhalb der "kleineren" Funktion liegt. Setzt man einen Wert aus dem Intervall in die beiden Funktionsgleichungen ein, erkennt man, dass innerhalb dieses Intervalls
größer ist als
. Sieht man natürlich auch in der Grafik oben.
In diesem Fall ist also zu berechnen:
Die von den beiden Graphen eingeschlossene Fläche ist also Flächeneinheiten groß.
Bemerkung: Der Begriff "Flächeneinheit" ist eine Verallgemeinerung. In der Aufgabenstellung waren ja keine Einheiten für die Achsen gegeben. Die Aufgabe "funktioniert" unabhängig davon, ob es sich um oder
oder Meilen oder ... handelt. Trotzdem hat eine Fläche natürlich irgendeine Einheit. Wir wissen halt nur nicht, welche ... Da man in der Mathematik üblicherweise gut mit Verallgemeinerungen leben kann, sagt man eben einfach "Flächeneinheit".
2)
In der Grafik ist zu sehen, dass diese Graphen von und
drei Schnittpunkte haben und damit zwei Flächenstücken einschließen.
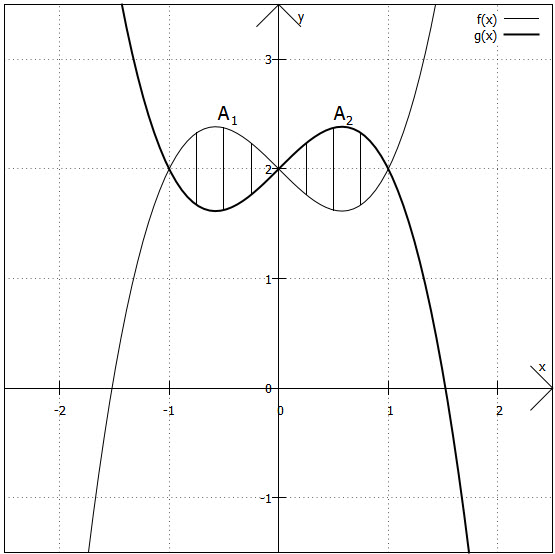
Schnittpunkte berechnen:
Lage der Funktion zwischen den Schnittpunkten bestimmen
Hier muss die Lage der Funktionen natürlich in beiden Intervallen überprüft werden: Im Intervall hat
größere Funktionswert, liegt als "über"
; im Intervall
ist es umgekehrt. Es kann also nicht einfach mit den Grenzen
und
gerechnet werden. Entweder man berechnet jeweils ein Integral für jedes Teilintervall oder - und das ist die "mathematischere" und kürzere Vorgehensweise - man überlegt sich, dass
und
punktsymmetrische Funktionen sind und damit die eingeschlossenen Flächen in den beiden Intervallen gleich sein müssen. D. h., man berechnet nur eines der beiden Integrale und multipliziert das Ergebnis mit
.
Das alles führt uns zu dem Integral
Die von den beiden Graphen eingeschlossene Fläche ist also Flächeneinheit groß.
3)
Die Funktionen und
mit
lassen sich wegen des Parameters nicht gut zeichnen, also versuchen wir es ohne Zeichnung ... Bitte beachten Sie, dass es sich bei beiden Funktionen einfach um quadratische Funktionen handelt;
ist ja nur eine Zahl.
Schnittpunkte berechnen
Lage der Funktion zwischen den Schnittpunkten bestimmen
Um zu bestimmen, welche Funktion im Intervall die größere ist, können wir beispielsweise die
einsetzen. Sie liegt sicher zwischen
und
. Es ergibt sich, dass im betrachteten Intervall
größere Funktionswerte hat als
Das alles führt uns zu dem Integral
Die von den beiden Graphen eingeschlossene Fläche ist also Flächeneinheiten groß, für
.
Zusatzaufgabe
Gefragt ist hier nach dem Flächeninhalt in Abhängigkeit von , nennen wir ihn
. Dieser ist zu maximieren. Der übliche Weg dafür ist, die entsprechende Funktion abzuleiten und dann die Nullstellen der Ableitungsfunktion zu bestimmen. Das machen wir auch hier so:
Von diesen drei Werten liegt nur im für
vorgegebenen Intervall.
Jetzt ist nur noch die Frage zu klären, ob bei tatsächlich ein Maximum der Funktion
liegt. Es könnte ja auch ein Minimum sein ... Der einfachste Weg hierfür ist, zu schauen, was für
passiert: Für diesen Parameterwert vereinfachen sich beide Funktionen zu
. Der von ihnen eingeschlossene Flächeninhalt ist also
und damit minimal. Da es außer den drei berechneten Werten und dem Rand des Intervalls keine weiteren Extremstellen geben kann und eine Funktion nicht an zwei nebeneinander liegenden Extremstellen jeweils ein Minimum haben kann, ist also klar, dass bei
tatsächlich ein Maximum liegt.