Übersicht:

6.1 Lineare Funktionen - Aufgaben

1. Aufgabe

Bestimmen Sie jeweils die lineare Funktion, die durch die beiden angegebenen Punkte verläuft, und zeichnen Sie die Funktionsgraphen in ein Koordinatensystem!

1) $A \left(2 \mid 12 \right)$ und $B \left(-1 \mid 3 \right)$		11) $A \left(5 \mid 3 \right)$ und $B \left(7 \mid 9 \right)$
2) $A \left(-1 \mid -1 \right)$ und $B \left(\dfrac {3}{2} \mid 4 \right)$		12) $A \left(-2 \mid 3 \right)$ und $B \left(7 \mid 2 \right)$
3) $P \left(0 \mid 5 \right)$ und $Q \left(10 \mid 0 \right)$		13) $A \left(0 \mid 22 \right)$ und $B \left(11 \mid 0 \right)$
4) $P \left(\dfrac12 \mid \dfrac16 \right)$ und $Q \left(\dfrac13 \mid \dfrac13 \right)$		14) $Q \left( \dfrac{19}{32} \mid \dfrac{8}{3} \right)$ und $P \left( - \dfrac{7}{5} \mid \dfrac{8}{3} \right)$
5) $A \left(2 \mid -3 \right)$ und $B \left(3 \mid 8 \right)$		15) $R \left( -7 \mid -55 \right)$ und $S \left( 1 \mid 9 \right)$
6) $R \left (22 \mid -4 \right)$ und $S \left (-14 \mid -4 \right)$		16) $P \left( 0 \mid 0 \right)$ und $Q \left( -36 \mid -\dfrac{24}{7} \right)$
7) $K \left(\dfrac{1}{2} \mid \dfrac{1}{4}\right)$ und $L \left(-2 \mid -\dfrac {7}{2} \right)$		17) $A \left( \dfrac{3}{2} \mid \dfrac{1}{4} \right)$ und $B \left( -5 \mid -\dfrac{7}{2} \right)$
8) $A \left (3 \mid \dfrac{7}{8} \right)$ und $B \left (-1 \mid -\dfrac18 \right )$		18) $P_1 \left( \dfrac{15}{8} \mid \dfrac{3}{4} \right)$ und $P_2 \left( - \dfrac{5}{2} \mid - \dfrac{1}{2} \right)$
9) $P \left (\dfrac14 \mid -8 \right)$ und $Q \left (-1 \mid 7 \right)$		19) $C \left( 17 \mid -\dfrac{17}{2} \right)$ und $D \left( -19 \mid \dfrac{53}{4} \right)$
10) $G \left (-3 \mid \dfrac {11}{6} \right)$ und $H \left(0 \mid -\dfrac16 \right)$		20) $P_1 \left( -25 \mid 3 \right)$ und $P_2 \left( 100 \mid -2 \right)$

2. Aufgabe

Stellen Sie jeweils fest, ob der angegebene Punkt $P$ auf der Geraden $f(x)$ liegt!

1) $P\left(2\mid 24\right)$ und $f(x)=15x-6$		6) $P\left(0{,}1\mid -9\right)$ und $f(x)=-296x$
2) $P\left(8\mid 9\right)$ und $f(x)=0{,}4x+6$		7) $P\left(0\mid 0\right)$ und $f(x)=288x$
3) $P\left(25\mid -560\right)$ und $f(x)=-63x+15$		8) $P\left(14\mid -4959\right)$ und $f(x)=-347x-101$
4) $P\left(14\mid 12{,}25\right)$ und $f(x)=\dfrac{7}{8}x$		9) $P\left(7\mid 88\right)$ und $f(x)=11x+24$
5) $P\left(-6\mid -21\right)$ und $f(x)=4x+3$		10) $P\left(22\mid -1\right)$ und $f(x)=\dfrac{12}{11}x-\dfrac{1}{9}$

3. Aufgabe

Beantworten Sie zu den linearen Funktionen jeweils die folgenden Fragen:

Wie ist das Steigungsverhalten der Geraden? Steigt/Fällt sie oder ist sie konstant?
Schneidet die Gerade die y-Achse bei einer positiven/negativen Zahl oder bei $0$ ?

Und das Alles: Ohne zu rechnen und zu zeichnen! Es geht nämlich bei dieser Aufgabe darum, den Funktionsterm zu verstehen und daraus Informationen über den Funktionsgraphen abzulesen, um z. B. Rechnungen plausibilisieren zu können.

Hinweis: Wer (noch) nicht weiß, was Potenzausdrücke, wie $(-754)^{39}$ , bedeuten, kann die Aufgaben 8) - 10) zurückstellen und erst das Kapitel Potenzen, Wurzeln, Logarithmen bearbeiten.

1) $f(x)=-1.234{,}5678$		6) $f(x)=-\dfrac{20}{-99}x$
2) $f(x)=\dfrac{83}{9}x-\dfrac{9}{83}$		7) $f(x)=2a-23$ mit $a\;\in\;\mathbb{R}^-$
3) $f(b)=\dfrac{64-8b}{64}$		8) $f(z)=(-754)^{39}z$
4) $f(a)=23a-2$		9) $v(x)=(-1)^{56}x+(-1)^{55}$
5) $g(x)=24\cdot(1-x)$		10) $u(x)=(-3)^3x+(-2)^2$

4. Aufgabe

Bestimmen Sie jeweils die Schnittpunkte der Geraden $g(x)$ mit den Koordinatenachsen!

1) $g(x)=24x-6$		6) $g(x)=\dfrac{5}{4}x+41$
2) $g(x)=\dfrac{4}{3}x-2$		7) $g(x)=\dfrac{6}{7}x-10$
3) $g(x)=-6x+8$		8) $g(x)=-12x$
4) $g(x)=x+48$		9) $g(x)=-\dfrac{3}{2}x-2$
5) $g(x)=15x-11$		10) $g(x)=-23$

5. Aufgabe

1) Gegeben sei die Funktion $f(x)=3x+5$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=2{,}5$ b) wenn $y=26$		6) Gegeben sei die Funktion $f(x)=-13x$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=5$ b) wenn $y=-104$
2) Gegeben sei die Funktion $f(x)=-x-\dfrac{1}{2}$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=31$ b) wenn $y=7{,}5$		7) Gegeben sei die Funktion $f(x)=-3x+\dfrac{5}{4}$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=\dfrac{3}{4}$ b) wenn $y=-16$
3) Gegeben sei die Funktion $f(x)=-4{,}5x+37$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=2$ b) wenn $y=130$		8) Gegeben sei die Funktion $f(x)=\dfrac{1}{20}x+20$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=18$ b) wenn $y=20{,}45$
4) Gegeben sei die Funktion $f(x)=\dfrac{3}{2}x-24$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=-5$ b) wenn $y=-20$		9) Gegeben sei die Funktion $f(x)=-\dfrac{2}{5}x+1$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=11$ b) wenn $y=0$
5) Gegeben sei die Funktion $f(x)=\dfrac{2}{3}x-\dfrac{5}{4}$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=2$ b) wenn $y=\dfrac{19}{12}$		10) Gegeben sei die Funktion $f(x)=-12x+\dfrac{11}{5}$ mit $x\in \mathbb{R}$ . Gesucht ist jeweils die fehlende Koordinate des Punktes $P(x\mid y)$ , a) wenn $x=-\dfrac{2}{5}$ b) wenn $y=4{,}2$

6. Aufgabe

Bestimmen Sie alle Lagebeziehungen der folgenden Geraden! Wenn sich die Geraden schneiden, berechnen Sie auch den Schnittpunkt!

$f_1(x)=3x-6$

$f_2(x)=-7x-6$

$f_3(x)=\dfrac{27}{9}x+1$

$f_4(x)=-\dfrac{21}{3}x-\dfrac{24}{4}$

7. Aufgabe

Die Grafik zeigt verschiedene Funktionsgraphen. Ermitteln Sie für jeden Graphen die Geradengleichung!

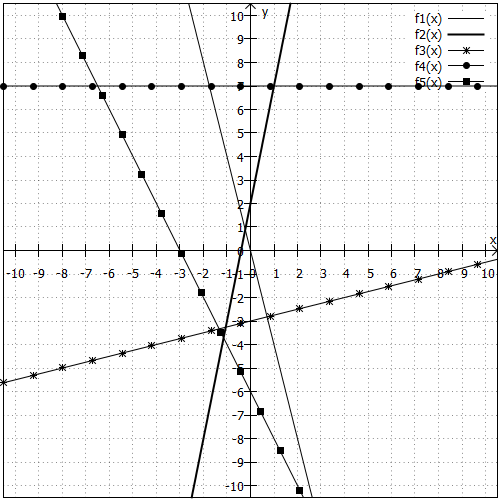
5 Geraden im Koordinatensystem

8. Aufgabe

Zwei gleich lange Kerzen werden gleichzeitig angezündet. Die erste Kerze hat eine Brenndauer von acht Stunden, die zweite eine von vier Stunden. Nach welcher Zeit ist die erste Kerze doppelt so lang wie die zweite?

9. Aufgabe

Für Profis: Welche Lagebeziehungen sind bei zwei Geraden im Raum möglich?