Übersicht:

22.1 Ableitungen - Aufgaben

1. Aufgabe

Ermitteln Sie grafisch die Ableitung dieser Funktion!
Bei dieser Aufgabe ist es nicht das Ziel, konkrete Zahlenwerte für die Steigung zu ermitteln; es soll lediglich die Größenordnung der Steigung an einer bestimmten Stelle im Vergleich zu anderen eingeschätzt werden, um ein Gefühl für das Konzept "Ableitung" zu bekommen.

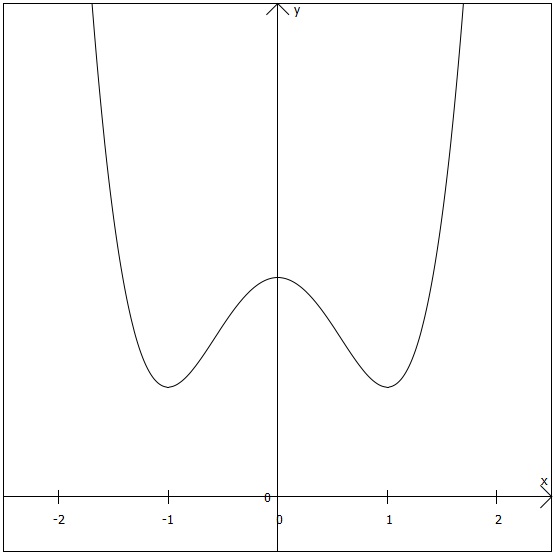
ein Graph im Koordinatensystem

2. Aufgabe

Leiten Sie die folgenden (einfachen) Funktionen ab! Geben Sie dabei jeweils die benötigen Ableitungsregeln an!

1) $f(x)=8x^2-21$		11) $f(x)=\dfrac{6}{x}$
2) $f(x)=-10x^3-x^2$		12) $f(x)=3\sqrt{x}-7$
3) $f(x)=-\dfrac{10}{9}x^{18}-11x$		13) $f(x)=x \cdot \sqrt{x}$
4) $f(x)=2x^2-x-1$		14) $f(x)=\dfrac{1}{x^2}$
5) $f(x)=-3x^4+16x^2+6$		15) $f(x)=-\dfrac{1}{12x^3}$
6) $f(x)=\dfrac{1}{4}x^4-\dfrac{1}{3}x^3+\dfrac{1}{2}x^2-x+5$		16) $f(x)=-\dfrac{17}{x^{19}}$
7) $f(x)=\dfrac{2x^{14}}{7}$		17) $f(x)=5\cdot \sqrt[4]{x}-x+1$
8) $f(x)=230x^{12}+17x^6-\frac{3}{5}x^5+400$		18) $f(x)=\dfrac{1}{6 \sqrt{x}}$
9) $f(x)=25x^4-66x^{\frac{1}{3}}-17x^{\frac{3}{2}}+e$		19) $f(x)=\dfrac{15}{\sqrt[5]{x^6}}$
10) $f(x)=x^{-3}+18$		20) $f(x)=7x^a+c$

3. Aufgabe

Leiten Sie die folgenden Funktionen mit der Produktregel ab!

1) $f(x) = \left(x-1\right)\cdot\left(\dfrac{47}{2}x^2+16x+7\right)$		11) $f(x) = 5{,}5^x\cdot x^5-5$
2) $f(x) = \left(13x^2+\dfrac{7}{5}x-18\right)\left(11x^2-\dfrac{15}{4}x-1\right)$		12) $f(x) = 19x^2\cdot\ln(x)$
3) $f(x) = \left(\dfrac{1}{8}x^3+5x\right)\cdot\sqrt{8}x$		13) $f(a) = -14\sqrt[4]{a}\cdot \log_4(a)$
4) $f(x) = 3x^2\cdot 7x^{\frac{1}{2}}+ex^{10}-105$		14) $f(x) = \dfrac{15}{x^2}\ln(x)+125$
5) $g(k) = \left(\dfrac{11}{6}k^2-k\right)^2\cdot 72$		15) $f(x) = 2x\cdot 3\sin(x)$
6) $f(x) = \left(4x^2-16\right)\sqrt{23x}-5$		16) $f(x) = \sin(x)\cdot\cos(x)-\dfrac{3}{\pi}$
7) $g(x) = 2^x\sqrt[10]{1024x}$		17) $f(x) = ax^2\cdot 5^3\sin(x)+17ax^3$
8) $f(x) = 23x^2\cdot e^x$		18) $f(x) = e^x\cdot\sin(x)$
9) $f(k) = \dfrac{5}{4}k^{12}\cdot e^k-1$		19) $f(x) = -6x^3\tan(x)-18$
10) $f(y) = \dfrac{16}{\frac{4}{3}y^7 e^{-y}}-\dfrac{14}{9}$		20) $f(s) = -\tan(s)\left(\dfrac{s}{\pi}+\cos(s)\right)$

4. Aufgabe

Leiten Sie die folgenden Funktionen mit der Quotientenregel ab!

1) $f(x)=\dfrac{x^{4}}{100-x}$		11) $f(w)=\dfrac{w-13}{-8\sqrt{w}}$
2) $f(x)=\dfrac{\dfrac{x^{2}}{9}+1}{-27x^{13}}$		12) $f(x)=\dfrac{12\sqrt{x}}{x-10}$
3) $f(q)=\dfrac{\left(-12q+7\right)^{4}}{144q^{2}-168q+49}$		13) $f(z)=\dfrac{2^{z}-1}{4^{z}}$
4) $f(x)=\dfrac{x^{3}}{x+5}$		14) $f(x)=\dfrac{21e^{x}}{7x+1}$
5) $f(x)=\dfrac{4x+2}{7x^{2}}$		15) $f(x)=\dfrac{17e^{x}-1}{34x^{2}}$
6) $f(x)=\dfrac{3x+5}{9x+2}$		16) $f(x)=-\dfrac{x^{2}+18}{18\lg\left(x\right)}$
7) $f(z)=\dfrac{23}{z^{-42}}$		17) $f(x)=\dfrac{\ln{\left(x\right)}}{x^{11}}$
8) $f(x)=\dfrac{x}{2x^{2}+4}$		18) $g(x)=\dfrac{-2\ln{\left(x\right)}}{x^{31}-x^{26}}$
9) $f(x)=\dfrac{15x^{2}-8x}{x^{3}+32}$		19) $f(y)=\dfrac{\pi\sin{\left(y\right)}}{-y^{2}}-12\pi$
10) $f(x)=\dfrac{8x+3}{4x-6}$		20) $y(t)=\dfrac{\sin{\left(t\right)}}{\cos{\left(t\right)}}$

5. Aufgabe

Leiten Sie die folgenden Funktionen mit der Kettenregel ab!

1) $f(x)=(2x+1)^7$		11) $f(x)=\sin^2(x)$
2) $f(x)=24\left(x+\dfrac{7}{8x}\right)^2$		12) $g(y)= \sqrt{\dfrac{121}{(72a-1)^2+5}}$
3) $f(x)=\dfrac{-63}{x^2-\frac{1}{x}}$		13) $f(x)=e^{x^2+\sqrt{x}}$
4) $g(x)=\sqrt{112x^3+97x}+16$		14) $f(x)=-36\sin\left(\cos(x)\right)$
5) $f(x)=\dfrac{1}{\sqrt{3x-6}}$		15) $f(x)=e^{\sin\left(-x^2+13\right)}$
6) $f(x)=\sqrt{(x+4)^3}$		16) $f(x)=85\ln\left(e^{3x}+x^2\right)-94$
7) $f(x)=\sqrt[3]{x+4}$		17) $f(z)=-\dfrac{3}{10}\sqrt{1+\cos\left(z^2\right)}$
8) $f(t)=\ln\left(\dfrac{5}{2}t^2+14\right)$		18) $f(x)=\sqrt{e^{\sqrt{x}-t}}$
9) $fx)=\ln\left(\dfrac{12}{7\sqrt{x}}\right)$		19) $f(x)=\dfrac{1}{ax+b}$
10) $f(x)=\ln\left(-42x^4-\dfrac{1}{18}x^3\right)$		20) $f(x)=\tan\left(c\cdot \sin(x)\right)$

6. Aufgabe

Leiten Sie die folgenden Funktionen ab! Geben Sie dabei jeweils die benötigen Ableitungsregeln an!

1) $f(x)= \dfrac{1}{2x+4}$		11) $f(x)=\dfrac{\sin(x)}{\cos(x^2)}$
2) $f(x)=\cos(7x+8)$		12) $f(x)=\ln\left(\dfrac{1}{x}\right)$
3) $f(x)=(x^2+1)\sin(x)$		13) $f(x)=\tan(x)-\cos(x)$
4) $f(x)=12xe^{x+10}$		14) $f(x)=\lg(x^2+2)$
5) $f(x)=e^{\sqrt{x}}$		15) $f(x)=\dfrac{3x^2-2x+1}{2}$
6) $f(x)=\dfrac{x^2+1}{x^3-1}$		16) $f(x)=e^{-\frac{x^2}{2}}$
7) $f(x)=\ln(x)+7^x+\sin(x)+5$		17) $f(x)=x \cdot e^{-5x^2}$
8) $f(x)=\cos(x^2)$		18) $f(x)=\dfrac{2}{2x^2-2}$
9) $f(x)=\cos^2(x)$		19) $f(x)=(3x^3+3)^{27}$
10) $f(x)=x^2 \cdot 10^x$		20) $f(x)=\ln\left(ax^3+bx^2+c\right)$

7. Aufgabe

Bestimmen Sie die Extrempunkte der folgenden Funktionen! Handelt es sich dabei jeweils um einen Tiefpunkt oder einen Hochpunkt?

1) $f(x)=2x^2-12x+24$		6) $f(t)=\dfrac{t^4-3t^3+5t-5}{t-1}$
2) $f(x)=- \dfrac{5}{2}x^2+10x+\dfrac{3}{8}$		7) $f(x)=\sqrt{-6x^2+16x+1}$
3) $f(x)=80x^2-16x+23$		8) $f(x)=e^{0{,}1x^2-8x-6{,}3}$
4) $f(x)=\dfrac{1}{3}x^3+2x^2-12x+6$		9) $f(x)=\dfrac{1}{2 \cdot \ln(10)} \cdot 10^{-8x^4+9x^2}$
5) $f(x)=\dfrac{1}{2}x^4-3x^2+1$		10) $f(x)=\ln \left(\dfrac{1}{2}x^3-12x\right)-15$

8. Aufgabe

1) Welche zwei Zahlen, deren Summe $100$ ist, haben das größte Produkt?

2) Welches Rechteck vom Umfang $36$ hat den größten Flächeninhalt?

3) Von einem Parallelogramm seien nur die Seitenlängen $a$ und $b$ bekannt, womit es noch nicht eindeutig festgelegt ist.
Fertigen Sie eine (beschriftete) Skizze an!
Bestimmen Sie die maximal mögliche Fläche eines solchen Parallelogramms!